临界事故报警系统仪表剂量计算方法研究
2017-04-18霍小东
邵 增,易 璇,霍小东
(中国核电工程有限公司,北京100840)
临界事故报警系统仪表剂量计算方法研究
邵 增,易 璇,霍小东
(中国核电工程有限公司,北京100840)
本文对临界安全基准实验国际评价中的迷宫实验进行了详细建模和验证计算,使用三维蒙特卡洛程序,采用两步法对中子探测器的读数进行了预测,并与实验结果进行了比较分析,统计了所有448个实验测点的计算偏差分布。通过总结临界事故报警系统在实际应用时位置选择和阈值设定的步骤,评价了本文所验证内容在上述过程中的作用。本文所开展的临界事故报警系统仪表剂量计算方法研究是临界事故报警系统设置中一项基础工作,可以为实际应用提供计算精度的参考数据,也可以应用于中子屏蔽设施的评价工作。
迷宫实验;中子探测器;剂量计算;临界事故;报警系统;阈值设置
核临界安全是核工业的特殊安全问题。天然铀经过富集或者乏燃料后处理后得到的钚,在对它们加工、处理、贮运和使用过程中,均紧密地伴随着临界安全问题。世界上所有从事核科技、核工业的国家,无一不对临界安全问题予以高度重视。尽管如此,在世界核工业的发展历程中,还是发生了多起临界事故,有的造成了人员伤亡的严重后果。因此,为了减小可能的临界事故造成的辐射受照量,需要在可能发生临界事故的区域设置临界事故报警系统(CAAS:Criticality Accident Alarm System),以向工作人员发出临界事故报警,让他们立即撤离受影响的区域。
设置临界事故报警系统需要考虑安装CAAS的地点、假想临界事故的特点以及CAAS的技术规格和布置,我国GB15146.9[1]中对此有详细要求。这些要求中一个很重要的方面是如何设置探测阈值,也就是在计数或者是通量、剂量达到何值时报警系统发出报警信号。可以对正常或者事故工况下设置报警系统处的通量、剂量以及探测器的响应函数进行计算评价,以此作为设置阈值的依据。因此对计算评价的可靠性的验证是很有必要也是很有意义的。
本文参考临界安全基准实验国际评价中的迷宫实验[2]的装置和结果,采用合适的计算方法对其进行模拟计算,比较了计算结果和实验结果的差异,证明了该计算方法可靠性较好,可以用于临界事故报警系统的阈值设定问题的计算分析。
1 实验介绍及程序建模
临界安全基准实验国际评价中迷宫实验是1982年在俄罗斯完成的,目的是为中子剂量估算程序提供基准数据。该实验的主体部分是一个大型混凝土的三段式迷宫,迷宫通道宽1.6m,高1.8m,四面均布置至少80cm厚的混凝土墙壁,其中第一段约长6.4m,第二段4.0m,第三段6.4m。实验通过在迷宫拐角处墙壁上贴附不同的材料或设置挡板,使得迷宫内中子通量分布发生变化,总共进行了6种实验方案的测量。
实验用中子源放置在迷宫的一端开口处。实验采用自发裂变的252Cf作为中子源,源的强度是每秒放出(5.66±0.18)×108个中子。锎源被封装在一个双层不锈钢的罐子里,总质量为3.2g。实验中,中子源被三角架固定在距地面90cm的高度。对每种布置的方案,分别使用了裸露中子源和置于直径30.5cm聚乙烯球内的中子源进行实验。
沿迷宫走向,均匀布置10个探测点,均位于迷宫通道正中位置,距地面高度为90cm。使用中子探测器,对迷宫内不同位置的中子通量进行了测量。中子探测器选用的是闪烁探测器,其主体部分是6LiI(Eu)晶体,利用反冲的α和3H粒子的电离效应来探测中子。实验中,探测器的探头外会包覆有一个聚乙烯球,球外包还可能有一层0.08cm厚的镉,根据包覆球的直径,分成2in、3in、5in、5in不含镉层、8in、10in和12in等7种类型。对每个测点,使用了多种类型的探测器分别进行了测量。
对本实验进行模拟,准确而直接的方法就是使用三维程序,详细建立实验方案的模型,在迷宫的测量点上模拟探测器的详细结构,然后统计出6Li(n,α) 反应的反应率。但实际上,这样的计算是很困难的,因为测点处的中子通量密度与中子源处相比,要小105~1010倍,即便采取有效减方差技巧,所需计算时间(单个测量点约需用时105min)也很难承受。
另外一种“两步走”的方法是,首先在迷宫模型中不模拟探测器,统计出来各测量点处的中子通量密度;然后建立中子探测器的详细模型,计算出中子探测器分能群的响应函数,然后每群相乘累加得到结果。使用两步法可以明显提高计算效率,缩短计算时间。大致估计,对本文所有探测点的计算,达到相近的统计标准偏差,两步法可以比直接模拟节省计算时间90%以上。
两步法能够应用的前提是,中子探测器对中子场的扰动是很小、可以被忽略的。经过计算发现,探测器对中子场的影响的确是很小的,其差别(0.6%)要远小于计算结果的统计偏差(1%~3%)。由于中子探测器对不同能量的中子的响应函数是不一样的,因此分为30群,计算出每一群的中子通量和响应函数,相乘然后各能群的计数相加就得到总的计数率。
对迷宫装置统计中子通量分布计算,本文使用三维蒙特卡洛程序MCNP5a进行模拟计算。迷宫模型的水平截面图见图1示。252Cf自发裂变的中子能谱在程序用Watt裂变进行模拟。对每个探测点,分30群统计中子通量及能谱分布。由于通道狭长,中子通量密度下降很快,最靠近中子源的探测点的中子通量密度约是最远点处的10000倍。因此,沿迷宫方向,共分成11个区域,分别设置倍增的中子重要性,并在每个探测点附近划出一小块区域设置倍增的中子重要性,这样最远探测点处的中子重要性为源中子重要性的16000倍。按照这种设定,可以在相对较短的时间内保证得到的所有探测点计数都满足误差要求的计算结果。

图1 迷宫模型水平截面图Fig.1 Horizontal section of the labyrinth model
探测器的响应函数也是使用三维蒙特卡洛程序MCNP5a进行模拟计算的,模型的垂直截面图见图2所示,模型中详细模拟了LiI晶体、TiO2层、玻璃窗、光导管、铝管等结构。实验中,为了满足中子探测器的量程和精度要求,在探头外包覆有一个聚乙烯球,球外包有一层0.08cm厚的镉,在计算响应函数时也进行了详细模拟。这里探测器的响应函数定义为单位时间单位中子通量密度下的探测器的计数,即发生6Li(n,α)反应的次数。

图2 探测器模型垂直剖面图Fig.2 Vertical section of the detector
探测器响应函数计算过程中,是针对不同能量的中子分别计算的,分为30个能群,对每个能群计算一个响应数,从而形成不同能群的响应函数。对每个能源的响应函数计算时,采用了160cm的大球面包围着探测器,球心与LiI晶体的中心重合。设置这样的面源,单能中子从160cm球面向内发射,发射角刚好与探测器的球面相切,计数统计中乘以截面积S即可得到归一化的单位中子通量。由于球面半径很大,远远大于探测器球面,可以认为中子束是平行的。这样便与中子通量密度的物理概念是吻和的:在空间r处单位时间内进入以该小球为中心的单位横截面积的小球的中子数。统计LiI晶体内发生6Li(n,α)反应的次数即可得到该能群的探测器响应函数。
2 计算结果及与实验值的比较
实验报告中给出了每个实验方案下,不同测点、包覆不同直径的聚乙烯球的探测器的计数率,计数率的单位为“次/s”,已经除去本底效应,计数率的总不确定度为3%。
本次验证工作对以下所有实验方案各测点的数据进行了计算和比较:
• Case1A:空的迷宫,裸露中子源;
• Case1B:空的迷宫,中子源置于聚乙烯球内;
• Case2A:迷宫第一个拐角处放置聚乙烯和镉层,裸露中子源;
• Case2B:迷宫第一个拐角处放置聚乙烯和镉层,中子源置于聚乙烯球内;
• Case3A:迷宫第一个拐角处放置聚乙烯层,裸露中子源;
• Case3B:迷宫第一个拐角处放置聚乙烯层,中子源置于聚乙烯球内;
• Case4A:迷宫两个拐角处放置含硼混凝土层,裸露中子源;
• Case4B:迷宫两个拐角处放置含硼混凝土层,中子源置于聚乙烯球内;
• Case5A:迷宫第二段内放置两个聚乙烯隔板,裸露中子源;
• Case5B:迷宫第二段内放置两个聚乙烯隔板,中子源置于聚乙烯球内;
• Case6A:迷宫第一个拐角处增加一个原方向延伸的密封段,裸露中子源;
• Case6B:迷宫第一个拐角处增加一个原方向延伸的密封段,中子源置于聚乙烯球内。
图3给出了所用到的探测器的响应函数,从图中可以看出:含镉层的探测器在超热中子区域基本没有响应函数,这是由于镉对热中子的吸收;包裹聚乙烯球的直径小的探测器在热能中子区域响应函数较大,而包裹聚乙烯球的直径大的探测器在快中子区域响应函数较大,这是由于聚乙烯的慢化作用和探测器发生6Li(n,α) 反应的截面特性导致的。
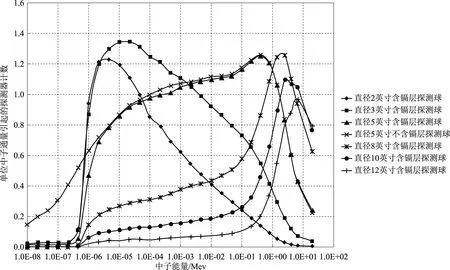
图3 探测器响应函数Fig.3 Response functions of the detectors
探测器的响应函数与实验方案各测点的分能群中子通量相乘,即可得到探测器读数的预测值。
以Case1A为例,该实验方案的计算结果与实验结果的比值列在图4中。在几种探测器的过比较中,外面包裹2in、3in聚乙烯球时,计算结果与实验读数符合最好;其他几种情况下计算结果偏大较多,偏差多数在+20%~+40%之间。
所有448个计算结果与测量结果的比值的统计情况如图5所示。从图5中可以看出,计算结果呈现出比实验结果偏大20%~40%的系统偏差。从统计结果来看,偏差在-10%至 +30% 之间的测点数目占总数的73.7%,偏差在-10%至+50%之间的测点数目占总数的93.5%。
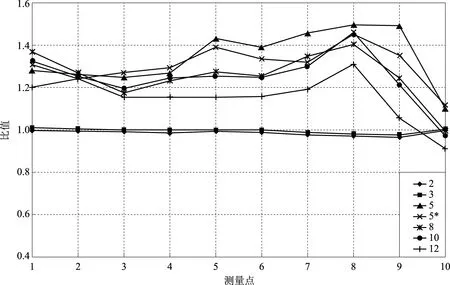
图4 Case1A计算结果与实验结果的比值Fig.4 Ratios of the calculation to experiment results of Case1A

图5 全部448个计算结果与实验结果的比值的统计柱状图Fig.5 Statistic of the total 448 ratios of the calculation to experiment results
造成计算结果与实验测量结果之间偏差的原因有很多。蒙卡程序本身的统计不确定度为5%左右,其他不确定度来源于实验测量的不确定度及建模引入的不确定度。实验测量结果的不确定度有3%,距离较远点的测量测量不确定度甚至有5%~10%,中子源强度的不确定度也有6%。计算所建立的模型已经尽可能真实的反映实验装置,但事实上存在很多不确定度因素,如构成迷宫的主要材料混凝土的密度、含水率,聚乙烯的密度、成分,空气的压力、湿度、温度等。迷宫实验中,中子经过多次散射才到达探测点,且强度衰减很大,此过程中与之发生反应的各种材料对实验结果影响较大。综合考虑实验中各参数的不确定度,该实验的计数率数据的相对标准偏差为8%~26%(1σ)。
例如,在Case1A的通量计算模型中,将混凝土的含水率增大一个标准偏差0.04g H2O/cm3,则会对探测器计数率预测值引入-5%~-20% 的偏差。又如,将包裹中子源的聚乙烯球密度增大一个标准偏差0.02g/cm3,则会对探测器计数率预测值引入+4%~-14%的偏差。
在实际应用此类剂量估计中,一般至少取30%的不确定度,从这个角度来看计算得到的偏差是与之相符的。个别测点的测量结果甚至超出了60%,可能存在一些不确定的因素,应该被忽略掉。
3 应用研究
迷宫实验的验证计算分析了中子探测器中探头所探测到的中子通量的计算方法可靠性。实际应用中,需要的可能是中子通量数据,有时需要的是剂量数据。由于剂量和通量之间可以采用ICRP第74号出版物给出的通量-剂量转换因子进行转化,因此上面对中子通量进行验证的结论也适用于剂量评价。
通过前面的分析比较可知,使用三维蒙卡程序分两个步骤评价探测器仪表的通量读数的方法,计算结果与实验结果符合较好,系统偏差在可接受范围内,可以认为该方法是可信可行的,可以在实践中进行使用。
对于临界事故报警系统,位置的设定和阈值的设置,对于该系统能否正确的发挥其应有的功能,有着决定性的作用。阈值即报警触发点的设置不能过高也不能过低,过高则可能对最小临界事故不报警,过低则对会很容易导致误报警,两种情况都会导致生产事故,造成人员伤亡以及经济损失。这里最小临界事故定义为:在2m处自由空气中的剂量吸收率为0.2Gy/min。
临界事故产生的辐射主要由裂变过程直接产生的γ和中子组成。次级γ辐射是由中子与临界源周围的结构材料和屏蔽材料的俘获反应发射出的。不同的临界装置观测到的瞬发辐射在大气中产生的中子和γ辐射剂量是有差别的。因此在评价最小临界事故时,2m处自由空气中的剂量吸收率0.2Gy/min为中子和γ辐射的总剂量,需要使用程序分别统计中子和γ辐射剂量,确定比例,然后才能计算出对应最小临界事故的裂变次数。
以后处理厂中一个贮存和操作钚溶液的设备室为例,该设备室拟安装某型临界事故报警仪。此报警仪的探测器为三个相互独立的6Li (ZnS/Ag)闪烁体中子探测器,能量响应为热中子,精度为±15%,量程为2μSv/h~20mSv/h。
为确定临界事故报警仪的安装位置和报警阈值,采用三维蒙特卡洛程序,按照下面的步骤进行分析计算:
1) 计算可能发生临界事故的钚溶液在临界值附近的中子泄漏能谱,作为固定中子源的能谱进行后续的计算;
2) 计算在可能的临界事故发生点2m处自由空气中的中子和γ辐射总的剂量吸收率为0.2Gy/min时对应的裂变次数,作为所考虑的最小临界事故,以此确定固定中子源的强度;
3) 根据步骤1和步骤2所确定的中子泄漏能谱和中子源强度,分析拟布置临界事故探测仪的几个位置的中子通量和能谱,并得到探测器的中子通量读数预测值;
4) 步骤3所计算出的中子通量读数预测值,乘以通量-剂量转换因子得到剂量读数预测值;
5) 根据步骤4计算得到的剂量读数预测值,考虑计算方法的可能偏差,与仪表量程比较,选择在量程范围内的探测点作为临界事故报警仪的布置点。
6) 报警阈值根据计算计算结果保守设置。同时分析探测范围内可能的本底照射(天然本底和核材料、核废料等衰变、自发裂变产生照射剂量)对探测器的读数影响,报警阈值应远高于本底读数,即临界事故报警仪的布置点应避开本底照射剂量强的位置。
7) 如果探测范围内有多个可能发生临界事故的设备,应综合考虑各个可能发生临界事故的设备、装置、容器发生最小临界事故时,最终确定中子探测器的位置及阈值设置。
在上面的步骤中,最重要的一步就是计算发生最小临界事故时中子通量的分布及探测器的读数预测值。在该步骤的计算中,可以采用本文验证迷宫实验所采用的计算方法,考虑可能的计算偏差,来设定临界报警仪的位置和报警阈值。
4 结论
本文对临界安全基准实验国际评价中的迷宫实验进行了验证计算,使用三维蒙特卡洛程序,采用两步法对中子探测器的读数进行了预测,并与实验结果进行了比较分析,统计了该计算的计算偏差分布。本文使用的计算方法结果与实验符合较好,偏差在可接受范围内,可以认为该方法是可信可行的,可以在实践中进行使用。本文总结了临界事故报警系统在实际应用时位置选择和阈值设定的步骤,评价了本文所验证内容在实际应用中的作用。本文所开展的临界事故报警系统仪表剂量计算方法研究是临界事故报警系统设置中一项基础工作,可以为实际应用提供计算精度的参考数据,也可以应用于中子屏蔽设施的评价工作。
[1] 国家技术监督局. GB15146.9-94. 反应堆外易裂变材料的核临界安全核临界事故探测与报警系统的性能及检验要求[S]. 1994.
[2] Mark Nikolaev, Natalia Prokhorova. Neutron fields in three-section concrete Labyrinth from Cf-252 source[R], NEA/NSC/DOC/(95)03/VIII, 2005.
The Dose Calculation Method Research for the Criticality Accident Alarm System Instrument
SHAO Zeng, YI Xuan,HUO Xiao-dong
(China Nuclear Power Engineering Co, Beijing, 100840)
This paper sets up a detailed model and does a validation calculation work for a labyrinth experiment in the international handbook of evaluated criticality safety benchmark experiments. A two-step method is used to predict the neutron detector’s readings using a three-dimensional Monte Carlo code. The calculation results are compared to the experiment readings, and the calculation biases statistic is done for the total 448 detect points. According to summarize the process in the location choosing and threshold setup for the criticality accident alarm system in the practice, the validation content done in this paper is evaluated. The dose calculation method research for the criticality accident alarm system instrument carried out in this paper is a base task in the criticality accident alarm system setup process. It can provide reference data for calculation precision in practice, and it can also be used for the neutron shielding configuration installations’ evaluation work.
Labyrinth experiment;Neutron detector;Dose calculation;Criticality accident;Alarm system;Threshold setup
2016-12-22
邵 增(1985—),男,山东滕州人,工程师,主要从事临界安全和次临界能源堆方面的研究
TL32,TL75
A 文章编号:0258-0918(2017)01-0106-07
