例谈建模方法在高中物理解题中的应用

浙江省台州市第一中学(324100) 黄 璟 ●

例谈建模方法在高中物理解题中的应用

浙江省台州市第一中学(324100) 黄 璟 ●

物理习题纵然千变万化、纷繁复杂，究其实质都是根据一定物理模型设计出来的．解题事实上就是一个寻找还原物理模型的过程．笔者作为一名高中生，将在本文中，结合典型的物理例题，略谈在物理解题中常用的几种建模解题法．

物理模型;建模方法;解题思维

所谓物理模型，就是指将现实中表面的、次要的条件舍去，将复杂具体的物理现象用简单抽象的、理想化模型来代替．在物理学习中，理想模型是一个绕不开的话题，题目是根据模型来设计的，解题需要倒推还原模型．利用建模思想，寻找理想模型，明晰解题思路，这是高中生在物理学习中最依赖的路径．模型化是解决物理问题最关键的一步，模型化正确、合理与否，直接关系到解题的速度与结果．在平时的物理学习中，笔者常用以下建模法:

一、化繁为简的抽象建模解题法

“从生活走向物理，从物理回归生活”是物理课程改革的新理念，近年来的高考出题很好地贯彻了这一理念，注重立足教材、强化基础、知能并重，出现了一些立意新颖、贴近生活的试题．此类题目，呈现的往往是一些日常生活中多见的现实的具体事物，在解题时需要将之抽象还原为一种理想化的物理模型．比如盘山公路可能看作是在高度一定时增加长度来省力的斜面;自行车把可以看作是轮轴;自卸货车的车厢可以看作是杠杆等等．

以2015年10月浙江省新高考物理卷为例，全卷只有两道题目直接以木块、小球等简单物体作为研究对象，大多试题都联系实际生活．如第8题的荡秋千，12题的快艇行驶，19题饲养员吹注射器，20题中汽车入避险车道，都需要学生具有基本的抽象还原建模能力．

比如第8题的荡秋千问题:“质量为30kg的小孩坐在秋千上，秋千离系绳子的横梁的距离是2．5m．小孩的父亲将秋千板从最低点拉起1．25米高度后由静止释放，小孩沿圆弧运动至最低点，求她对秋千板的压力．”在解题时，须将题中的秋千进行合理简化，变成一定约束条件下的物理模型，将小孩抽象成质点，秋千的运动简化成非匀速圆周运动，问题就能迎刃而解．

二、化难为易的类比建模解题法

一些物理题，看似疑难生疏，解题似乎需要建立新的复杂模型．但这些新模型，往往是在旧模型的基础上发展变化而来的．此时，可运用类比联想的方法，去寻找物理规律与题设信息中相似相同之处，将复杂的物理现象和过程转化为理想的、等效的物理模型，把问题迁移到已有的知识体系，把新情景问题转化为简单和熟悉的模型来解决．

近些年来，物理频现“信息题”，对考生创新能力提出了更高的要求．初看此类题目，似乎无从着手，若采用类比转化的方法，将“生题”变成“熟题”，就能柳暗花明，快速做出题目．

例:天文学家根据天文观察宣布了下列研究成果:银河系中可能存在一个“大黑洞”，距“黑洞”60亿千米的星体以2000km/s的速度绕其旋转，接近“黑洞”的所有物质即使速度等于光速也逃脱不了其引力作用，试计算“黑洞”的最大半径．

在中学物理课堂上，没有专门就“黑洞”概念进行详细解析，这是一个新难情景，根据题意，星体既然绕其旋转，其绕“黑洞”作圆周运动的向心力，显然是由万有引力提供的，据万有引力定律，可知“黑洞”是一个有质量的天体．设“黑洞”和转动星体的质量分别为M和m，两者距离为R，利用万有引力定律和向心力公式列式:，得到GM=v2r;题中还有一个信息:即使是等于光速的物体也逃脱不了“黑洞”引力范围，据此信息，可以设想速度等于光速的物体恰好未被“黑洞”吸入，可类比近地卫星绕地球作圆周运动，设“黑洞”半径为r，用类比方法得到GM=c2r(C为光速)，所以

三、化此为彼的数学建模解题法

物理模型是客观存在的实物的一种类似，对客观实物进行同等数量的描述就是以物理模型为对象建立数学模型的过程．物理解题过程，实际上是将物理模型转化为数学模型、物理问题转化为数学问题，运用数学的方法进行推理和运算，求解后再次还原为物理结论的过程．在高考物理卷，计算题分值占到总分将近一半，其中一些难题如果巧妙应用数学方法，能收到事半功倍的功效．

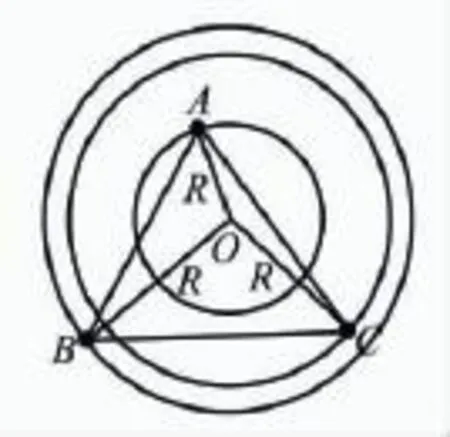
以2015年安徽物理高考压轴题即有名的“三星题”为例:由三颗星体构成的系统，忽略其他星体对他们的作用，存在着一种运动形式:三颗星体在相互之间的万有引力作用下，分别位于等边三角形的三个顶点上，绕某一共同的圆心O在三角形所在平面内做相同角速度的圆周运动(图示为A、B、C三颗星体质量不相同时的一般情况)．若A星体为2m，B、C两星体的质量均为m，三角形的边长为a，求A星体所受合力FA;B星体所受合力大小FB;C星体的轨道半径RC;三星体做圆周运动的周期T．此题有多种解法，比如数学解析法、质心坐标法等，也可构建几何图形，运用数学三角函数中的余弦定理来解决物理力的矢量三角形，运用相似三角形对应边成比例的几何关系解决物理数据，不管哪种解法都突出了数学性，都需要用数学思维来思考、分析物理问题，体现了数学方法在物理解题中的妙用，充分说明了数学与物理的紧密联系．

物理是一门具有严密逻辑性的自然科学，光靠题海战术、生搬硬套是无法提高解题能力的．作为一名高中生，必须学会常用的建模方法，做到融会贯通、巧妙运用，发展灵活多变的创新思维，为当下乃至今后的学习发展打下扎实基础．

G632

B

1008－0333(2017)06－0068－01