露天爆破震动诱发地下洞室顶板失稳的非线性机理分析1)
2017-04-17闫长斌侯世杰郑州大学土木工程学院郑州450001郑州市轨道交通有限公司郑州450003
闫长斌 徐 晓 侯世杰(郑州大学土木工程学院,郑州450001)(郑州市轨道交通有限公司,郑州450003)
露天爆破震动诱发地下洞室顶板失稳的非线性机理分析1)
闫长斌∗,2)徐 晓∗侯世杰†
∗(郑州大学土木工程学院,郑州450001)
†(郑州市轨道交通有限公司,郑州450003)
开挖爆破是诱发工程岩体失稳的重要因素.根据露天与地下联合开采特点,将地下洞室顶板简化为水平简支梁,基于非线性理论分析方法建立了露天爆破震动扰动诱发地下洞室顶板失稳的突变理论模型,导出了其失稳判据条件和临界安全厚度,探讨了爆破震动幅值、主频、围岩特性等主要因素对地下洞室顶板临界安全厚度的影响.以甘肃厂坝铅锌矿群采空区顶板安全厚度分析为例,计算得到了露天与地下采场之间顶板的临界安全厚度.研究结果表明:露天爆破扰动诱发地下洞室顶板失稳过程具有非线性和不连续性特征,顶板临界安全厚度不仅取决于岩体工程特性,而且与爆破震动幅值、主频等多重因素有关,这与实际情况是吻合的.
露天爆破,地下洞室,顶板失稳,突变理论,临界安全厚度,影响因素
引言
开挖爆破震动诱发岩体动力失稳破坏是一个高度复杂的非线性和不连续过程,是内因(岩体特性、结构形式等)和外因(外界扰动类型及其特性等)联合作用的结果.系统从稳定向不稳定状态转化是一个量变到质变的过程.当量变累积至一定程度,达到临界平衡状态,任何微小外界扰动(爆破震动)都可能使系统跨越临界点,发生失稳破坏,即所谓“一根稻草压垮一匹骆驼”.根据现代非线性科学观点,当系统处于高度不稳定状态时,任何微小扰动都会被放大,微扰动在临界点附近会转变成巨扰动,正是这种巨扰动驱动着事物向新的状态演化[1-2].
无论地下生产还是露天开采,地下洞室(巷道、采场或采空区)顶板岩体长期遭受爆破震动和采动载荷 (加、卸载)的反复作用.根据资料显示[3],砂岩、泥灰岩的疲劳强度仅为其极限强度的60%左右,且岩体越软,强度降低越显著.距离爆源较远或爆破规模不大时,外界扰动表现为爆破震动作用,岩体不会直接发生失稳破坏.然而在反复爆破震动加、卸载作用下,岩体中临界、亚临界裂纹不断扩展,岩体力学性能弱化,动力损伤逐步累积[4-5].损伤累积达到一定程度,岩体将处于临界平衡状态,此时爆破震动即可诱发顶板失稳破坏,危及人员和设备安全.这种失稳破坏现象,许强等[2]称之为临界微扰失稳效应,往往是突发的、无前兆的非线性动力过程,与有前兆的渐进破坏形式相比,更具危害性.
采掘过程中,频繁爆破作业诱发巷道、采场动力失稳现象屡见不鲜[6-8],国内采用炮采的矿井50%以上都存在着严重的巷道围岩动力失稳破坏问题[9].例如,新汶华丰矿2001年连续在3406、3407工作面发生了2次重大冲击地压事故,造成了严重的人员伤亡及财产损失.南芬露天铁矿运输主平硐在生产中长期经受爆破震动影响,出现掉块等局部失稳现象[10].大冶铁矿尖林山矿体,由于受地压和周边反复爆破震动作用,巷道支护开裂,矿岩塌落[11].另外,刁虎[12]报道了某矿山采场下覆的废石运输平硐受频繁生产爆破的影响,出现局部失稳征兆.基于此,有必要针对露天与地下联合开采作业特点,开展爆破震动,特别是反复爆破扰动下地下洞室顶板安全性研究,建立露天爆破扰动下地下洞室顶板动力失稳机理分析方法,为预防露天爆破震动诱发的地下洞室顶板失稳灾害提供科学指导.
1 露天爆破震动诱发地下洞室顶板动力失稳的突变模型
露天爆破震动对地下洞室顶板的影响,如图 1所示.根据地下洞室几何尺寸、岩体强度、完整程度及地质特征,可将顶板视为平面应力问题,在轴向上截取单位厚度,将其简化为水平简支梁(图2).图2和图3中,P(x,t)为作用在梁上的竖向爆破震动载荷;P0为梁的自重载荷,P0=mg,其中m为梁的质量,g为重力加速度;T为水平地应力;L为梁的跨度;h为顶板的厚度(或称为高度).
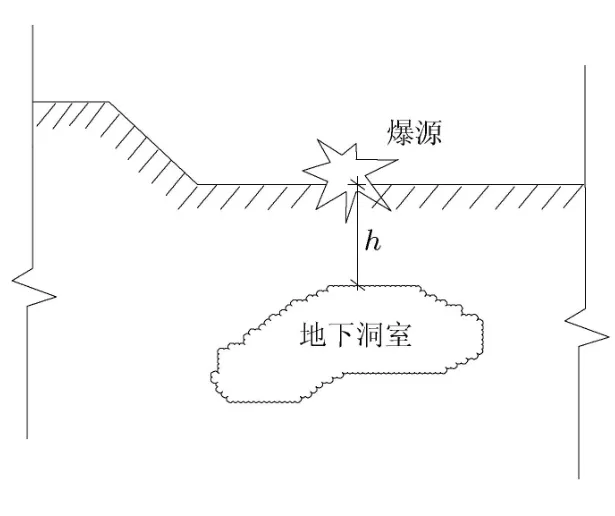
图1 露天爆破对地下洞室的影响示意图
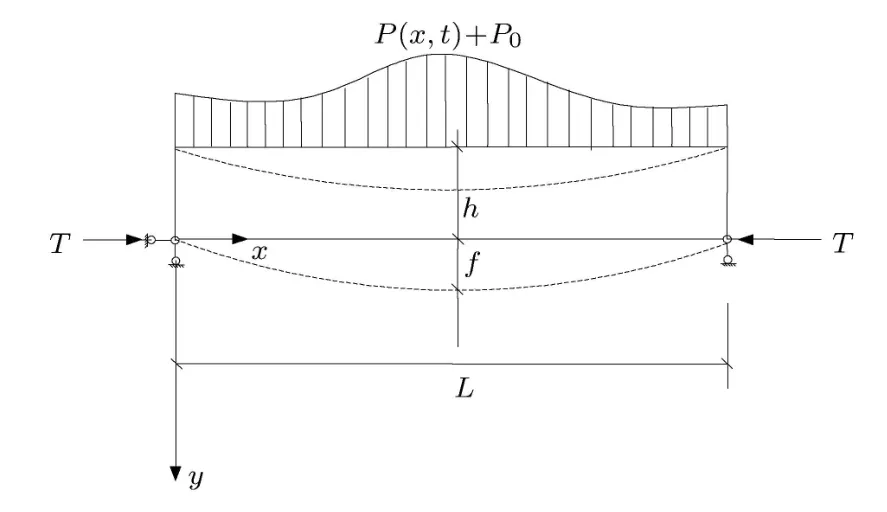
图2 简化的水平简支梁力学模型
为建立梁的震动平衡方程,取梁中的某一微元段dx进行具体分析,如图3所示.在y方向上考虑微元段的动力平衡,根据达朗贝尔原理,可得以下方程
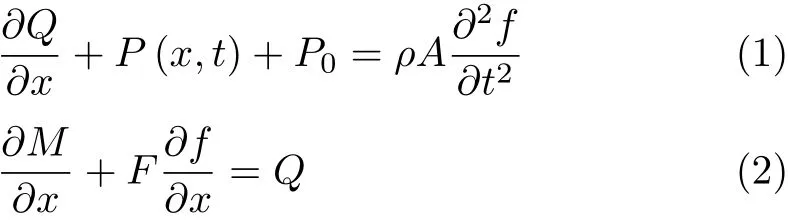
式中,ρ为介质的密度;A为梁的横截面面积;F,Q和M分别表示梁的水平内力、竖向内力和弯矩;f为梁的挠度.

图3 微元体受力示意图
根据Euler-Bernoulli假设[13],可得

式中,E和I分别为梁的弹性模量和惯性矩,c为阻尼系数,且c>0.f0为梁的初始挠度.
可将爆破震动载荷P(x,t)简化为[14]

式中,Pmax为爆破震动载荷的幅值,ω为爆破震动载荷的频率.由此,可以假定
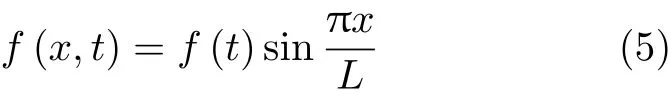
将上式代入式(3),并整理,得到
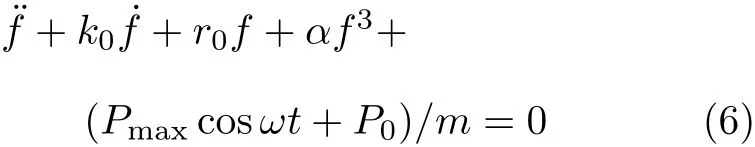
式中,k0=cω0>0,r0=ω20,其中ω0为未考虑自重载荷时梁的初始自振频率;α表征结构的非线性系数,α的取值不同,结构的动力响应亦不同[15].
当k0和α很小,且梁为小变形时,方程(6)为弱非线性,其解近于线性方程的解
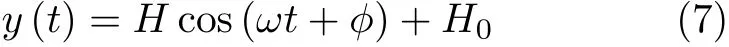
式中,H0是梁自重载荷引起的振幅变化,这里假定H0为常量;H为梁的动力响应振幅;φ是由于阻尼c引起的响应滞后,显然当c=0时,φ=0.
将上式代入方程(6),忽略高阶小量和三次谐波项,并令一次谐波项的系数相等,整理后可得到
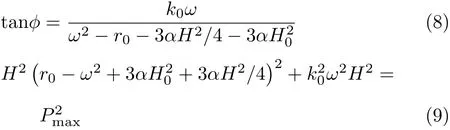
对式(9)进行微分同胚变换[16],并消去关于H2的二次项,得到

式中
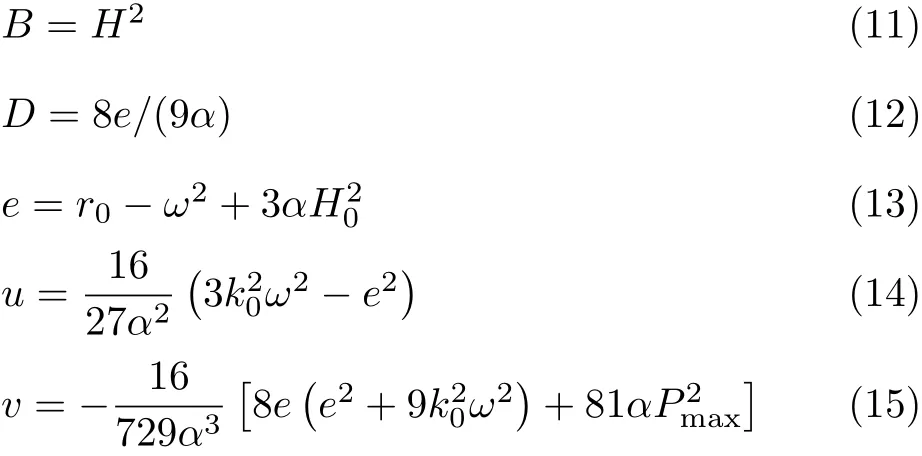
式(10)即为标准尖点突变流形方程,其中B+D称为状态变量,u和v称为控制变量.由于状态变量由B和D两个变量组成,故式(10)实际上是由两个尖点突变组合而成的双尖点突变.
2 露天爆破震动诱发地下洞室顶板动力失稳的判据条件
由突变理论可知[15],结构处于临界状态(位于分叉点集上)时,微小的外界扰动就能使结构的响应发生突变,故突变模型的分叉集方程即为发生突变的充分条件.
对式(10)求导,可得

联立式(10)和式(16),可得分歧点集方程

将式(14)和式(15)代入式(17),可得

式(18)就是露天爆破作业产生的地震波诱发地下洞室顶底板突变失稳的充分条件.因此,考虑自重载荷情况下,露天爆破作业产生的地震波能否诱发地下洞室顶底板发生动力失稳破坏,不仅取决于爆破震动幅值和主频率,而且还与工程结构特点、岩体内部属性等因素有关.
当爆破震动幅值及主频率越过分歧点集的位置时,顶板结构动力响应振幅将随之发生突跳,从而诱发结构系统产生失稳破坏.由于式(16)只在u≤0时成立,即只在u≤0条件下才能跨越分歧点集,因而由式(14)可得地下洞室顶板结构系统发生失稳的必要条件是

3 露天爆破震动作用下地下洞室顶板的临界安全厚度
由固体力学理论可知,图3中梁的挠度大小f与梁的厚度h成反比.在露天爆破规模等其他条件一定的情况下,h越大,f就越小,地下洞室顶板就越安全,越不容易发生失稳破坏;反之则顶板越容易产生失稳破坏.因此,梁的厚度存在一个临界值h0,当梁的厚度h>h0时,爆破震动作用时地下洞室顶板不发生失稳破坏;当梁的厚度h<h0时,地下洞室顶板就发生失稳破坏.
将式(18)进一步展开,整理后可得

其中

对方程(20)进行求解,由于考虑α>0,舍去小值,得到

在单位宽度条件下,即A=h.整理后得到
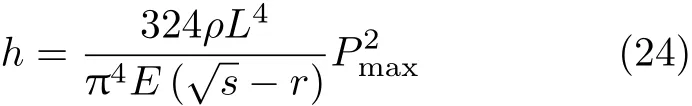
此时得到的h即为考虑自重载荷时爆破震动作用下地下洞室顶板的临界安全厚度h0.
3.1 爆破震动幅值和主频率对顶板临界安全厚度的影响
由爆破地震测试和上述推导可知,爆破震动幅值Pmax对地下洞室顶板临界安全厚度h0影响较大,震动主频率也有一定影响.考虑自重载荷,给定ω01=51.2rad/s,ω=157rad/s,ρ=3000kg/m3,c=0.10,L=20m,E=6GPa,由式(13)~式(15)和式(24)可得

h0与Pmax的典型曲线如图4所示.当ω取不同值时,h0与Pmax之间的关系式亦不同.岩体内任一点的动应力为σ=ρc0v0.由此可推导出临界安全厚度h0与质点震动速度之间的关系,还可根据萨道夫斯基公式进一步确定临界安全厚度与爆破药量之间的关系.
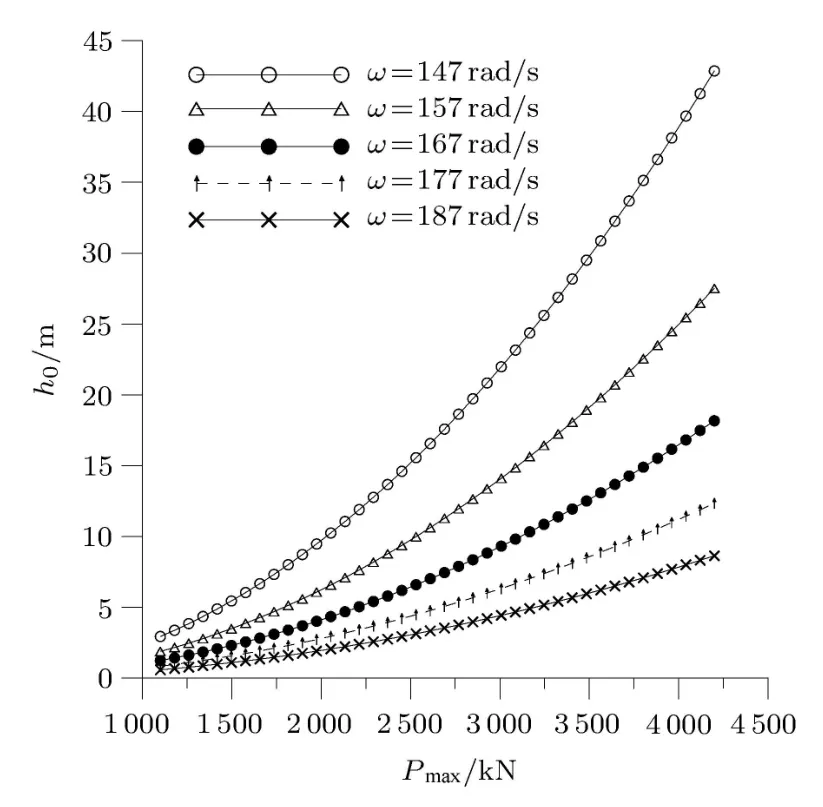
图4 h0与Pmax的关系曲线
由图4可知:(1)随Pmax增大,h0逐渐增大,且呈非线性陡增趋势.由此可见,h0对Pmax的变化较敏感.露天爆破规模越大,震动强度越大,越容易诱发地下洞室顶板失稳破坏.(2)当Pmax一定时,随ω减小,h0逐渐增大,说明ω也会影响地下洞室顶板的稳定性.主频率越低,破坏效应越强,顶板失稳破坏可能性越大.当ω接近或等于地下洞室顶板的自振频率ω01时,则系统发生“共振效应”,此时h0趋向无穷大,即发生失稳破坏,丧失承载能力.现场测试结果和爆破地震动效应最新研究成果证明了这一点.
3.2 围岩特性对顶板临界安全厚度的影响
由式(24)可见,岩体弹性模量E与h0存在定量关系.随着E增加,h0逐渐减小.说明围岩的强度越大,岩体完整性越好,地下洞室顶板越稳定,反之越容易发生失稳破坏.爆破震动会对岩体造成一定损伤,使得岩体强度和完整性降低,从而降低岩体弹性模量,增加岩体失稳几率.对于露天爆破作业,在爆破震动反复作用下,随着岩体损伤非线性累积增长,岩体弹性模量不断降低.当岩体弹性模量降低至一定程度,地下洞室顶板厚度达到临界安全厚度,此时爆破震动会使地下洞室顶板发生失稳破坏.图5为h0与E之间的关系.由此可见,岩体弹性模量越大,临界安全厚度越小,地下洞室顶板越安全;相反,岩体弹性模量越小,临界安全厚度越大,地下洞室顶板越易发生失稳破坏.当岩体弹性模量一定时,爆破震动强度越大,临界安全厚度越大,顶板也越容易发生失稳.
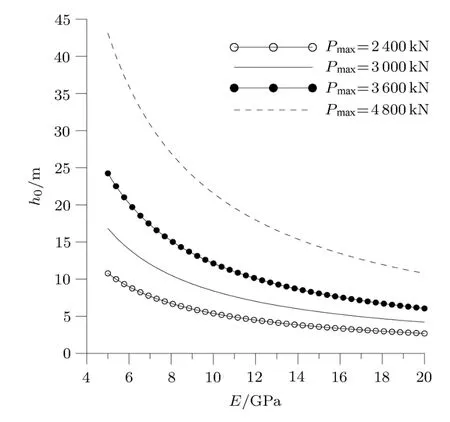
图5 h0与E的关系曲线
3.3 循环爆破产生的岩体累积损伤效应及其影响
爆破开挖诱发的扰动与损伤,特别是循环爆破作业产生的震动累积损伤效应,必然导致岩体完整性降低,岩体质量和力学参数弱化,从而威胁岩体工程稳定性.爆破损伤程度不同,受扰动程度不同,岩体完整性降低程度不同,岩体力学参数的弱化程度也不同.如何定量描述爆破累积损伤效应与岩体力学参数劣化之间的关系,是岩石力学与爆破工程界亟待解决的重要难题之一.闫长斌等[17-18]基于声速降低率η建立了岩体爆破损伤度D、岩体完整性系数Kv之间的关系

式中,E0为爆破前岩体的弹性模量;E为爆破后岩体的等效弹性模量;v0为爆破前岩体的声波速度;v为爆破后岩体的声波速度.
频繁爆破作用下,岩体爆破损伤不断累积扩展,每一次爆破后岩体的损伤增量ΔD均可用声速降低率来描述.假定爆破次数为n,第i次爆破后岩体声波速度为vi,则第i次爆破后的岩体损伤增量ΔDi(i=1,2,…,n)为

由此可得,第i次和n次爆破后的岩体力学参数Ei及E′

E′为i为n时的值.式(28)就是以岩体声速降低率为基准量表征的爆破累积损伤效应与岩体力学参数劣化之间的关系模型.在频繁爆破开挖作业过程中,应用声波测试对岩体爆破损伤及其累积程度进行监测,根据测试得到的爆破后岩体声速降低率,利用式(28)计算每次爆破后岩体的累积损伤与劣化后的岩体力学参数.从而可以将式(28)的计算结果代入到式(24)中,计算每次爆破后顶板是否安全.
4 算例分析
厂坝铅锌矿是我国特大型铅锌矿床之一.由于长期疯狂的群采破坏,留下许多未处理的群采空区.这些采空区相互贯通形成了跨度很大的地下暗空场,对露天转地下生产形成巨大的安全隐患.若在暗空场上面布置采场,进行露天爆破采掘作业,需要预留合理的采空区顶板厚度,否则会酿成生产事故.例如,1995年至 1997年间曾连续发生三次塌陷事故.将地下采空区的顶板简化为如图3所示的力学模型,根据建立的突变模型和地下洞室顶板临界安全厚度计算公式,可以确定地下采空区顶板的临界安全厚度.
计算所需有关爆破震动和岩体参数均来自现场观测或室内试验,具体参数见表1.将表1中的数据代入式(15)、式(17)、式(18)和式(20),可计算得到地下采空区的临界安全厚度h0为19.82m.

表1 计算所用参数
现场观测得到的顶板安全厚度均大于20m,而实际发生失稳破坏的顶板厚度80%以上小于18m.现场观测结果表明,本文确定的顶板临界安全厚度h0值是合理的.当采空区顶板的厚度小于这个值时,就有发生失稳破坏的危险.由于在计算中假定梁的宽度为单位宽度,因此计算结果是偏于保守的.
5 结 论
(1)生产过程中露天爆破震动诱发地下洞室产生的动力失稳现象,具有明显的突跳性、不连续性和非线性特点,借助非线性理论分析方法揭示其内在机制是可行的.
(2)根据建立的地下洞室顶板动力失稳破坏突变理论模型及导出的判据条件可知,考虑自重载荷情况下,爆破震动是否会诱发地下洞室顶板产生失稳不仅取决于爆破震动条件(幅值和主频等),还与爆破次数、上覆层载荷、地应力、围岩特性等其他因素有关.
(3)爆破震动幅值、主频率以及围岩特性对地下洞室顶板临界安全厚度具有明显影响.临界安全厚度对爆破震动幅值较敏感,露天爆破规模越大,震动强度越大,越容易诱发地下洞室顶板失稳破坏.爆破震动频率越低,破坏效应越强,地下洞室顶板失稳破坏可能性也越大.
(4)岩体强度越高,完整性越好,弹性模量越大,临界安全厚度越小,地下洞室顶板越安全,反之越容易发生失稳破坏.循环爆破产生的岩体累积损伤效应,使得岩体完整性和弹性模量不断降低,对顶板安全性不利.
1 黄润秋,许强.工程地质广义系统科学分析原理及应用.北京:地质出版社,1997
2 许强,黄润秋,王来贵.外界扰动诱发地质灾害的机理分析.岩石力学与工程学报,2002,21(2):280-284
3 Freumd LB.Dynamic Fracture Mechanics.Cambridge:Cambridge Press,1990
4 杨国梁,杨仁树,车玉龙.周期性爆破震动下围岩的损伤累积效应.煤炭学报,2013,38(s1):25-29
5 闫长斌,王贵军,石守亮等.岩体爆破损伤声波测试信号频谱特征的小波 (包)分析.岩石力学与工程学报,2010,29(71):1496-1502
6 Innaurato N,Mancini R,Cardu M.On the inf l uence of rock mass quality of blasting work in tunnel driving.Tunneling and Underground Space Technology,1998,13(1):81-89
7 闫长斌,王泉伟,李国权等.邻近爆破对矩形岩柱稳定性影响的突变理论分析.爆炸与冲击,2010,30(5):556-560
8 谢承煜,罗周全,贾楠等.露天爆破震动对临近建筑的动力响应及降振措施研究.振动与冲击,2013,32(13):187-193
9 姜耀东,赵毅鑫,宋彦琦等.放炮震动诱发煤矿巷道动力失稳机理分析.岩石力学与工程学报,2005,24(17):3131-3136
10 孙豁然,肖海军,王运森等.爆破动载荷下平硐稳定性的研究.金属矿山,2001,(12):15-19
11 马建军.软岩巷道在周边爆破作用下的稳定性研究.北京:北京理工大学,2004
12 刁虎.爆破震动对废石运输平硐稳定性的影响与综合治理.矿业快报,2001,(6):11-13
13 杨桂通,张善元.弹性动力学.北京:中国铁道出版社,1988
14 魏德敏.拱的非线性理论及其应用.北京:科学出版社,2004
15 Yan CB,Xu GY.The destabilization analysis of overlapping underground chambers induced by blasting vibration with catastrophe theory.Transactions of Nonferrous Metals Society of China,2006,16(3):735-740
16 Zeeman EC.Catastrophy theory.Scientif i c American, 1976,234(4):65-83
17 闫长斌,徐国元,杨飞.爆破动载荷作用下围岩累积损伤效应声波测试研究.岩土工程学报,2007,29(1):88-93
18 闫长斌,李国权,陈东亮等. 基于岩体爆破累积损伤效应的Hoek-Brown准则修正公式.岩土力学,2011,32(10):2951-2957
(责任编辑:刘希国)
NONLINEAR MECHANISM ANALYSIS OF UNDERGROUND CHAMBER ROOF INSTABILITY INDUCED BY OPEN BLASTING VIBRATION1)
YAN Changbin∗,2)XU Xiao∗HOU Shijie†∗(School of Civil Engineering,Zhengzhou University,Zhengzhou 450001,China)†(Zhengzhou Metro Co,Ltd,Zhengzhou 450003,China)
The blasting excavation is an important inf l uencong factor for the instability of engineering rock mass.In view of the characteristics of combined mining for open-pit and underground,catastrophe theory models of the underground chamber roof instability induced by open blasting disturbance are built by taking the underground chamber roof as a horizontal simply supported beam based on the non-linear theory.The instability criteria and the critical safe thickness of the underground chamber roof are derived according to the catastrophe theory models.At the same time,the important inf l uencing factors for the critical safe thickness of the underground chamber roof,such as the amplitude and the key frequency of the blasting vibration,and the characteristics of the surrounding rock are discussed.The critical safe thickness of the roof between the open-pit and underground stopes is obtained by a safe thickness analysis of Changba Pb-Zn deposit group mined-out area roofs in Gansu province as an example.It is shown that the dynamic instability of the underground chamber roof is obviously nonlinear and discontinuous,while the critical safe thickness of the underground chambersroof not only depends on engineering geological characteristics of the roof,but also on other multiple factors, for example,the amplitude and the key frequency of the blasting disturbance,as is consistent with the actual situation.
open blasting,underground chamber,roof instability,catastrophe theory,critical safe thickness, inf l uence factors
TD32,TU311
A
10.6052/1000-0879-16-240
2016-07-19收到第1稿,2016-08-28收到修改稿.
1)国家自然科学基金(U1504523)和河南省高等学校重点科研项目(15A410001)资助.
2)闫长斌,博士,副教授,主要从事岩石力学与工程研究工作.E-mail:yanchangbin 2001@163.com
闫长斌,徐晓,侯世杰.露天爆破震动诱发地下洞室顶板失稳的非线性机理分析.力学与实践,2017,39(1):45-50
Yan Changbin,Xu Xiao,Hou Shijie.Nonlinear mechanism analysis of underground chamber roof instability induced by open blasting vibration.Mechanics in Engineering,2017,39(1):45-50
