定时截尾缺失数据样本下Lomax分布总体形状参数的估计与检验

龙 兵， 朱全新， 习长新

(1.荆楚理工学院 数理学院 湖北 荆门 448000; 2.南京师范大学 数学科学学院 江苏 南京 210023)

定时截尾缺失数据样本下Lomax分布总体形状参数的估计与检验

龙 兵1， 朱全新2， 习长新1

(1.荆楚理工学院 数理学院 湖北 荆门 448000; 2.南京师范大学 数学科学学院 江苏 南京 210023)

在定时截尾缺失数据样本下研究了Lomax分布形状参数的估计和假设检验.在尺度参数已知的条件下给出了形状参数的极大似然估计，证明了估计量的相合性和渐近正态性，并给出了形状参数的置信区间和假设检验，最后通过蒙特卡洛随机模拟说明了估计的优良性.

Lomax分布； 定时截尾； 缺失数据； 极大似然估计

0 引言

Lomax分布在寿命试验数据处理中起着重要的作用，很多统计学者对此分布进行了深入的探讨.文献[1]研究了Lomax分布参数极大似然估计的存在性和估计量的收敛性.文献[2]在完全样本下研究了两个参数及分位数的区间估计和假设检验.文献[3]研究了基于缺失数据样本下Lomax分布尺度参数的估计，并说明了确定最优置信区间的方法.文献[4-8]在不同损失函数下，当尺度参数已知时，讨论了形状参数的贝叶斯估计问题.在利用统计方法处理试验数据时，如何根据缺失数据进行统计推断是统计分析中的一个重要问题.文献[9-12]讨论了多种分布在缺失数据样本下的参数估计问题，而对Lomax分布在定时截尾数据缺失样本下的参数估计还没有人研究.本文假设尺度参数已知，在定时截尾数据缺失样本下给出了形状参数的极大似然估计，证明了估计量的相合性和渐近正态性，并给出了形状参数的置信区间和假设检验.

1 极大似然估计及其渐近性质

设样本观测数据来自Lomax分布总体，其密度函数为

(1)

其中:θ为形状参数；λ为尺度参数；在本文中假设尺度参数已知.

现对上述Lomax分布总体进行n次独立观测，并到T0时刻停止，每个样本观测值以概率1-p缺失,以概率p被观测.用(Zi,δi,αi),i=1,2,…，n表示总体观测值，其中：Zi=min(T0,Xi),Xi表示第i个样品的寿命；αi=I{Xi≤T0}-I{Xi>T0}，即观测到具体的失效时间αi=1，否则αi=-1，并且第i个样品观测数据缺失时记δi=0，否则δi=1.

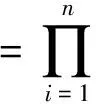
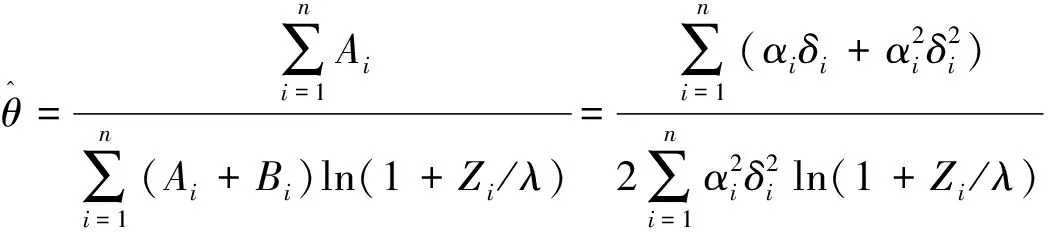
(2)

由θ的极大似然估计可得到如下定理.

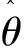
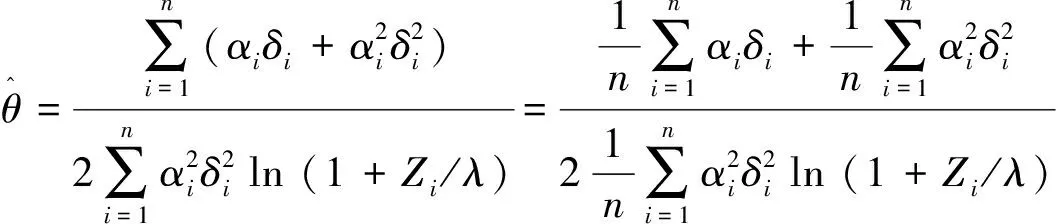
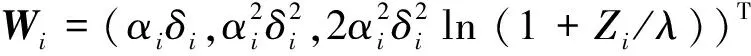
在坚持家庭经营为主的条件下，每家每户拥有1.33 hm2左右的雷竹林，通过轮流覆盖栽培，能取得较好的经济效益，从而可以稳定竹农的种竹积极性。从竹林可持续经营角度来看，3～4年形成一个覆盖轮回较为合理，竹林经营面积1.33 hm2是接近合理轮回的面积。为使农户家庭劳动力与竹林达到最优配置状态，进而使家庭收入最大化，农户可选择转入竹林扩大经营规模，或转出剩余劳动力从事其他行业的生产。

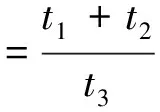
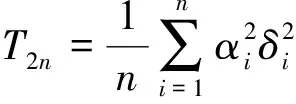
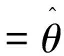
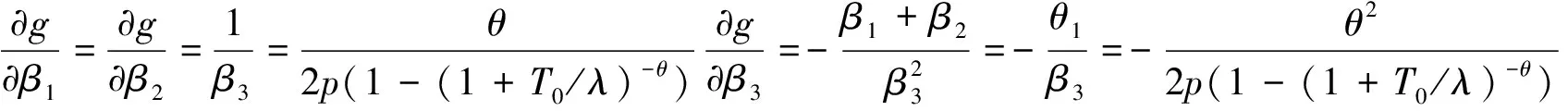
即

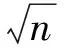
2 区间估计及假设检验

在实际中，对参数真值范围的研究，可以归结到参数的置信区间问题.对于本文中讨论的问题可得到如下定理.

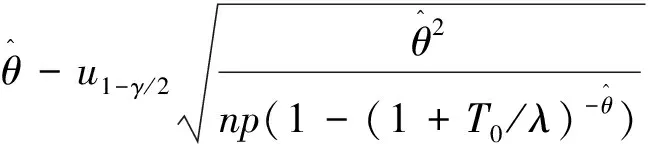
其中uγ为标准正态分布的γ下分位数.

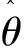
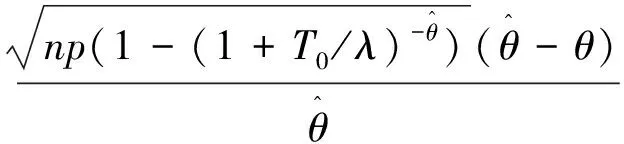
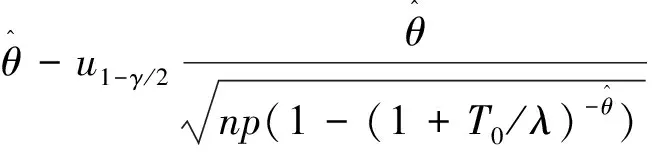
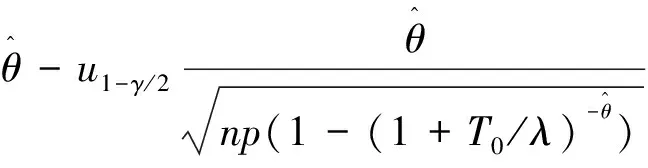
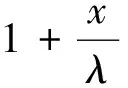
因为xp是θ的单调递减函数，因此当λ已知时，p分位数xp的置信水平为1-γ的近似置信区间为

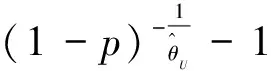
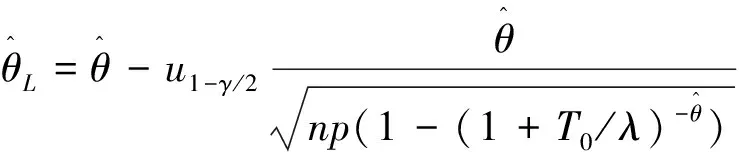
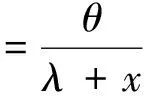
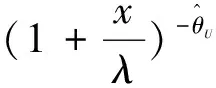
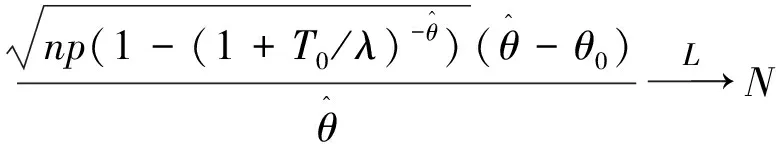
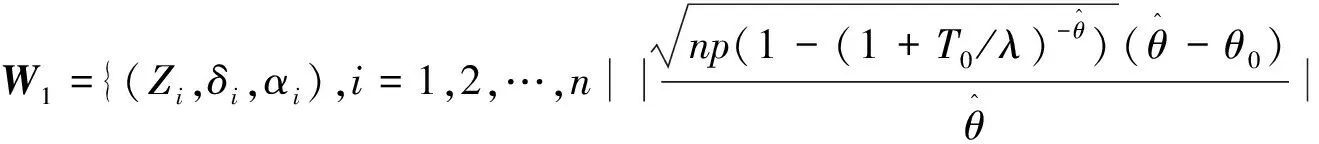
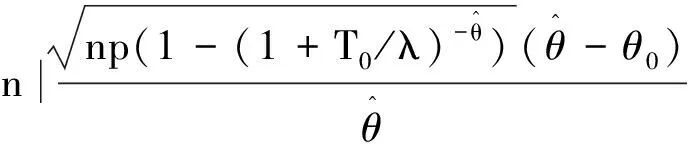
3) 对于假设检验问题H0:θ<θ0↔H1:θ≥θ0.同理可得，对于给定的显著性水平γ(0<γ<1)，检验的拒绝域为

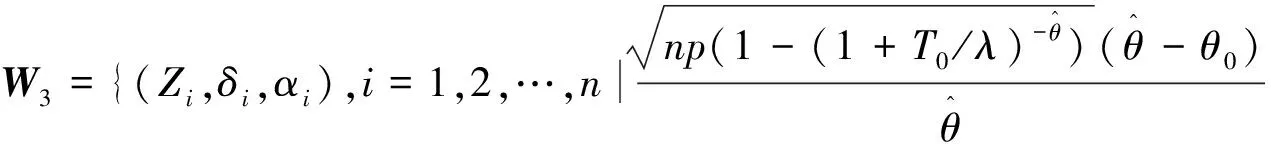
根据定理2可以得到两个独立Lomax分布总体形状参数之差的区间估计和假设检验问题.

3 随机模拟

当λ分别取1.2和2时，在形状参数θ取不同真值的情况下，通过随机模拟的方法，产生一个服从Lomax分布(1)的样本，且样本容量n=100.取缺失概率1-P=0.1，置信水平1-γ=0.95，对于给定截尾时间T0，利用上述样本可以得到参数θ的估计，以上过程重复1 000次，可以得到参数估计的均值、均方误差、置信区间的上下限均值及覆盖率，模拟结果见表1.对形状参数的估计都很接近参数真值，并且均方误差较小.θ的真值介于下限均值与上限均值之间，覆盖率很接近近似置信水平0.95.

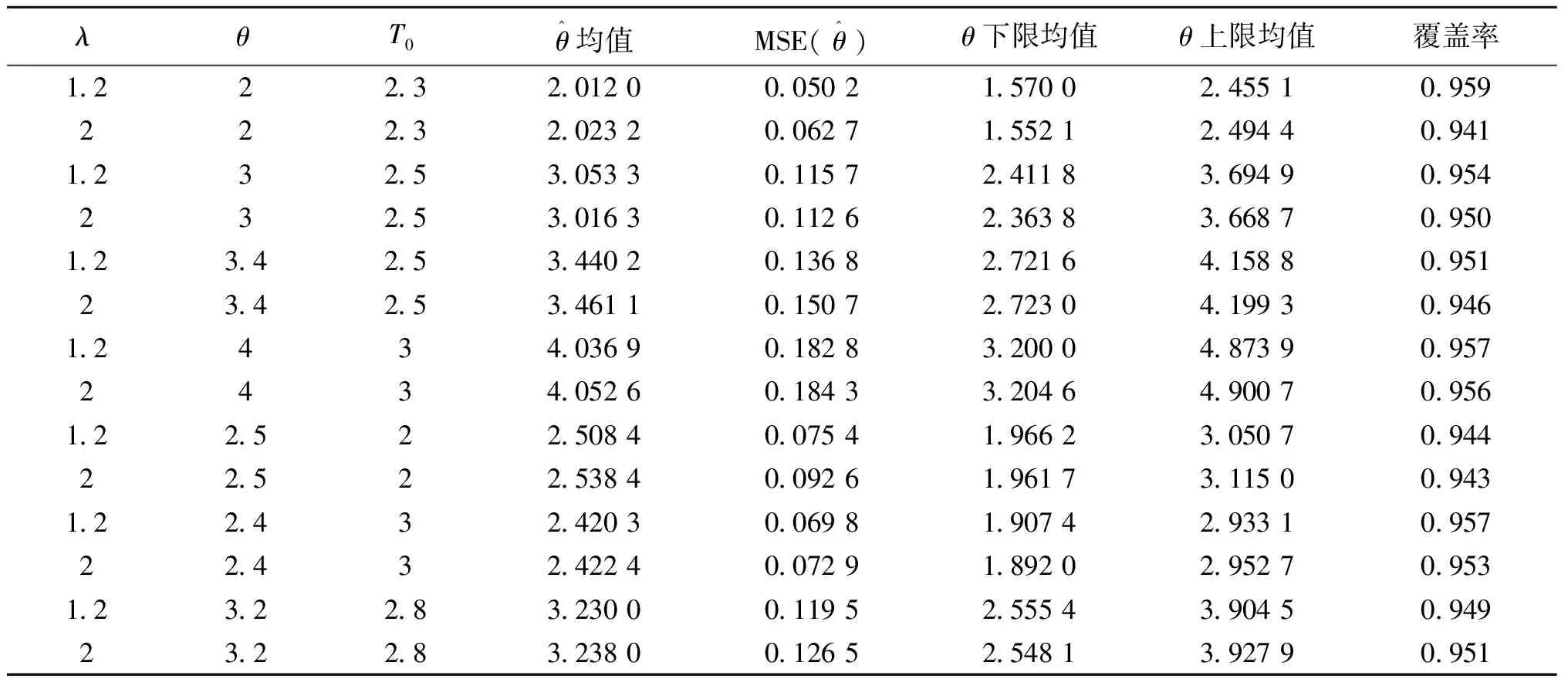
表1 参数估计的均值、均方误差(MSE)、置信区间的上下限均值及覆盖率

[1] 李开灿，刘大飞，林存津.Lomax分布极大似然估计的两点研究[J].数学杂志，2016，36(1)：207-213.

[2] 龙兵.两参数Lomax分布中参数的区间估计和假设检验[J].江西师范大学学报(自然科学版),2014,38(2):176-179.

[3] 龙兵.缺失数据样本下Lomax分布尺度参数的估计[J].统计与决策，2014,19：21-23.

[4] 龙兵,张明波. 定数截尾下Lomax分布失效率和可靠度的贝叶斯估计[J].华南师范大学学报(自然科学版), 2016, 48(2)：102-106.

[5] 肖小英，任海平.熵损失函数下两参数Lomax分布形状参数的Bayes估计[J].数学的实践与认识，2010，40(5):227-230.

[6] 周明元.对称熵损失函数下两参数Lomax分布形状参数的Bayes估计[J].统计与决策，2010(17):8-10.

[7] 姚惠，谢林.不同损失下Lomax分布形状参数的Bayes估计[J].数学杂志，2011,31(6)：1131-1134.

[8] 姚惠.Linex损失下Lomax分布形状参数的Bayes估计[J].统计与决策，2011(16):173-175.

[9] 赵志文，王思洋，王瑞庭，等.定时截尾下具有部分缺失数据两个指数总体参数的估计与检验[J].吉林大学学报(理学版)，2009，47(1)：26-30.

[10]龙兵，王秋节，习长新.具有部分缺失数据的两个Pareto分布总体参数的估计和检验[J].贵州大学学报(自然科学版)，2016，33(1)：9-12.

[11]何朝兵.右删失左截断数据下离散威布尔分布的参数估计[J].郑州大学学报(理学版)，2016，48( 2) : 18-23.

[12]赵志文，赖民，宋立新，等.具有部分缺失数据的两个对数正态分布总体参数的估计与检验[J].统计与决策，2009(20)：7-9.

(责任编辑：方惠敏)

Shape Parameter Estimation and Hypothesis Testing of Lomax Population under Type I Censoring Sample with Missing Data

LONG Bing1， ZHU Quanxin2， XI Changxin1

(1.SchoolofMathematicsandPhysics,JingchuUniversityofTechnology,Jingmen448000,China； 2.SchoolofMathematicalSciences,NanjingNormalUniversity,Nanjing210023,China)

The shape parameters estimation and hypothesis test were studied on Lomax distribution under type I censoring sample with missing data. Maximum likelihood estimation of the shape parameter was discussed on condition that the scale parameter had been known, and the consistency and asymptotic normality of the estimators were proved. Moreover, the confidence interval and hypothesis test of shape parameters were given. Finally, Monte Carlo simulation was used to illustrate the excellent performance of the estimator.

Lomax distribution; type I censored sample; missing data; maximum likelihood estimation

2016-08-27

国家自然科学基金项目(61374080)；湖北省教育厅科学研究项目(B2016264).

龙兵(1973—)，男，湖北荆门人，副教授，主要从事数理统计的研究,E-mail:qh-longbing@163.com.

O212.7

A

1671-6841(2017)02-0019-05

10.13705/j.issn.1671-6841.2016213