不确定条件下的均衡市场

郑颖春， 杨云锋

(西安科技大学 理学院 陕西 西安710054)

不确定条件下的均衡市场

郑颖春， 杨云锋

(西安科技大学 理学院 陕西 西安710054)

建立了跳过程为非爆炸性计数过程的跳扩散模型，讨论了完备市场下的财富优化与市场均衡.利用随机分析的方法，构建了唯一的等价鞅测度，证明了存在唯一的优化投资组合及最优消费过程，给出了最优财富过程、最优消费过程和优化投资组合.给出了均衡市场的特性，证明了均衡市场的存在性和唯一性.

跳扩散过程； 均衡市场； 完备市场； 消费过程； 财富优化

0 引言

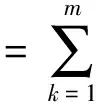
许多学者对类似的优化问题进行了研究.文献[2]讨论了在完备市场的资产连续.文献[3]讨论了资产服从poisson跳扩散时的财富最大化问题.文献[4-8]讨论了市场连续或跳扩散时的风险最小化问题.文献[9-12]讨论了风险资产的方差满足Heston模型下的优化问题，并将跳过程进行了推广.本文研究在完备市场中，股票支付连续红利的条件下，跳过程为计数过程的跳扩散模型时的财富优化问题[13]，讨论所建金融市场下的均衡问题.

1 金融市场

设市场m=(r(t),ρi(t),μi(t),σi(t),φi(t),Si(t),i=1,2)是标准且完备的，无风险资产B(t)和风险资产Si(t)满足微分方程(Ft,0≤t≤T)，{W(t),0≤t≤T}，且

dSi(t)=Si(t-)((μi(t)-ρi(t))dt+σi(t)dW(t)+φi(t)dM(t)，i=1,2，

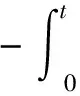
假设 函数λ(t)，r(t)，μi(t)，σi(t)，φi(t)，ρi(t)都是可测、有界的，且满足：

1)λ(t)>0，r(t)≥0，σi(t)>0，ρi(t)≥0，φi(t)>-1，φi(t)≠0(i=1,2)；

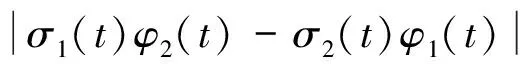
3) 存在c2∈(0,+∞)，使得

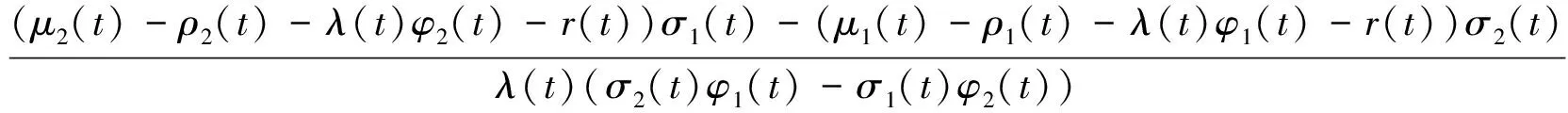
由假设知，存在θ1(t),θ2(t)满足μi(t)-λ(t)φi(t)-r(t)-σi(t)θ1(t)+λ(t)φi(t)θ2(t)=0,i=1,2.得到命题1和命题2.

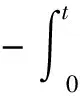
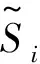
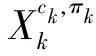
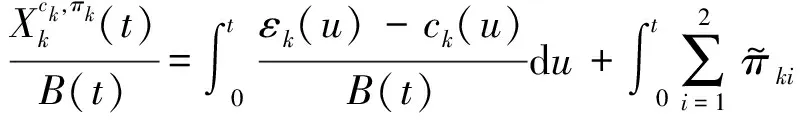
(2)

2 主要结论

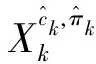
(3)

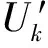
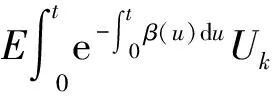
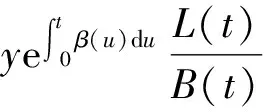
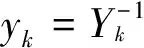
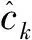
(4)

故

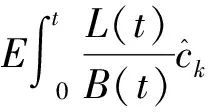
(5)

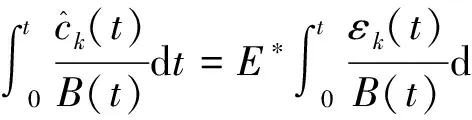
(6)

由假设条件知方程组(6)有唯一解πk=(πk1,πk2),(ck,πk)∈Ak，使得

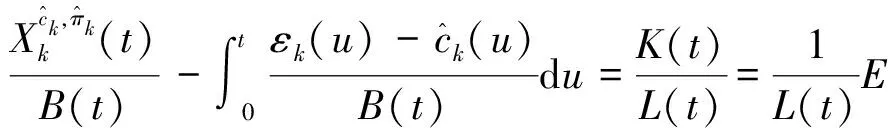
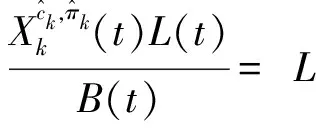
定理2 标准的完备的市场m是均衡的充分必要条件是

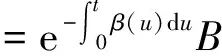
(7)

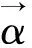
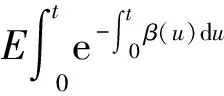
(8)

此时，投资者k的最优消费过程可表示为

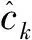
(9)

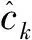
(10)

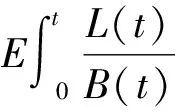
(11)

则由市场均衡的条件，可得

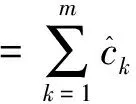
(12)

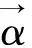
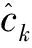
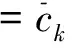
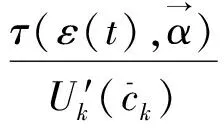
(13)

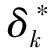
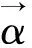
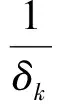
(15)

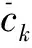
定理4 优化问题

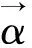
(16)

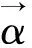
证明 依据效用函数的定义, 可得

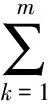
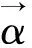
因此(9)式是优化问题(16)的解,且有

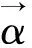
(17)

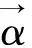
定理5 标准的完备的市场m=(r(t),ρi(t),μi(t),σi(t),φi(t),Si(t),i=1,2)是均衡的充分必要条件是

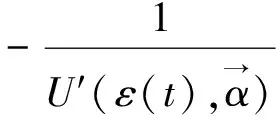
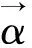
(18)

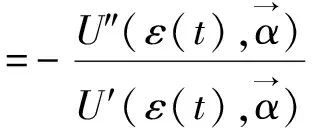
(19)

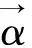
(20)

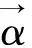
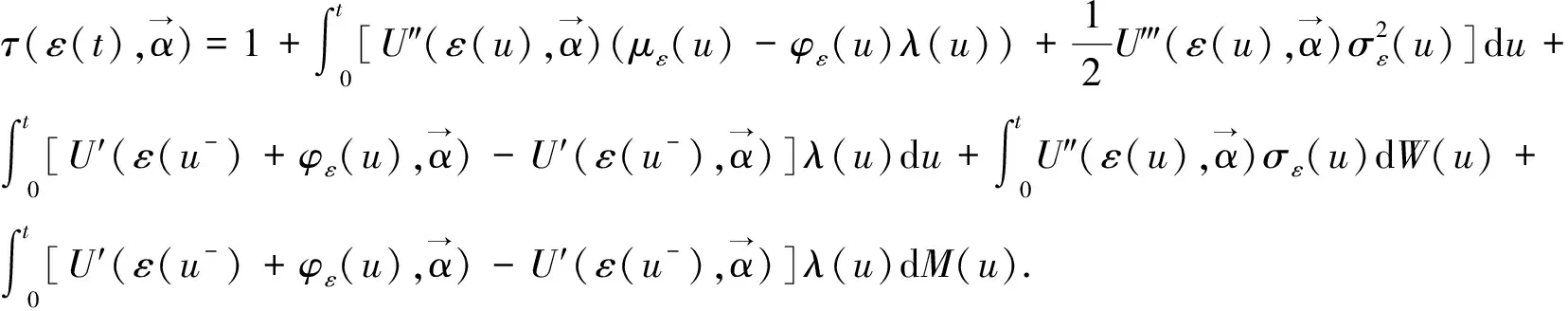
比较式(20)和(21)可以得到式(18)和(19).

3 结论

[1] MARKOWITZ H. Portfolio selection[J]. The fournal of finance， 1952,7(1):77-91.

[2] ROBERT C. Optimum consumption and portfolio rules in a continuous time model[J].Journal of tconomics theory,1970, 3(4):373-413.

[3] JEANBLANC J M，PONTIER M. Optimal portfolio for a small investor in a market model with discontinuous prices[J]. Applied mathematical and optimization, 1990,22(1):287-310.

[4] FOLLMER H, LEUKERT P. Efficient hedging:cost versus shortfall risk[J].Finance and stochastics,2000,4 (2):117-146.

[5] NAKANO Y. Minimization of shortfall risk in a jump-diffusion model[J]. Statistics and probability letters,2004, 67(1) :87-95.

[6] 杨云锋,金浩. 完备市场下亏空风险的最小化[J]. 经济数学,2011,28(4):30-33.

[7] PHAM H. DynamiLp-hedgingindiscretetimeunderconeconstraints[J].Siamjournaloncontrolandoptimization, 2000, 38(3): 665-682.

[8] 王永茂,王丹,龙梅,等.跳-扩散风险模型下的最优投资和再保策略[J].郑州大学学报(理学版),2015,47(1):50-54.

[9] 杨鹏.Heston模型下最优投资-消费策略选择[J].郑州大学学报(理学版),2016,48(1):17-22.

[10]杨云锋,金浩. 不完备市场下的财富优化[J]. 江西师范大学学报(自然科学版),2012,36(3):245-248.

[11]杨云锋,夏小刚,杨秀妮. 跳跃扩散过程的期权定价模型[J].数学的实践与认识,2010,40(6):40-45.

[12]杨云锋,金浩. 波动率随机时的财富优化模型[J]. 统计与决策. 2014,404(8):32-35.

[13]DUFFIED.Dynamicassetpricingtheory[M].NewJersay:PrincetonUniversityPress,2007.

[14]BACKK.Martingalepricing[J].Financialeconomics,2010, 2(2):235-250.

[15]RIEGERMO.Optimalfinancialinvestmentsfornon-concaveutilityfunctions[J].Economicsletters, 2012, 114(3):239-240.

(责任编辑：方惠敏)

Equilibrium Market under Uncertainty

ZHENG Yingchun, YANG Yunfeng

(SchoolofScience,Xi′anUniversityofScience&Technology,Xi′an710054,China)

The problem of wealth optimization and equilibrium under complete financial markets was considered based on the jump-diffusion model with nonexplosive counting process. Resorting to stochastic analysis method, the uniqueness of the equivalent martingale measure and the optimal investment portfolio and consumption process was proved. Moreover, the optimal wealth process, the optimal consumption and portfolio process were also supplied. Finally, the existence and uniqueness of equilibrium in the financial market was provided once the characterization of an equilibrium market was given.

jump-diffusion process; equilibrium market; complete financial market； consumption process； wealth optimization

2016-08-25

国家自然科学基金项目(71473194)；陕西省教育厅科学研究计划项目(16JK1500)；陕西省科技新星计划项目(2013XJXX-40).

郑颖春(1979—)，女，陕西蓝田人，讲师，主要从事最优化理论研究，E-mail:zhychun1979@163.com；通讯作者：杨云锋(1978—)，男，陕西永寿人，副教授，主要从事金融数学、时间序列研究，E-mail:yangyunfeng_1978@126.com.

O211.6

A

1671-6841(2017)02-0014-05

10.13705/j.issn.1671-6841.2016211