随机噪声干扰下的迭代学习控制器设计

夏 浩，张丽杰

(大连理工大学 控制科学与工程学院，辽宁 大连 116023)

(*通信作者电子邮箱lijie_zhang@outlook.com)

随机噪声干扰下的迭代学习控制器设计

夏 浩，张丽杰*

(大连理工大学 控制科学与工程学院，辽宁 大连 116023)

(*通信作者电子邮箱lijie_zhang@outlook.com)

为解决迭代学习控制系统中随机噪声扰动问题，提出基于无限脉冲响应(IIR)数字滤波器的优化迭代学习控制器设计方法。该方法在首次迭代时对系统输出误差进行基于小波变换的两轮实验法滤波；其次根据小波滤波获得的输出误差确定部分及原误差信号作为输入输出辨识出等效IIR线性滤波器，并重构优化误差目标函数，进一步利用优化方法对迭代学习控制器优化设计；最后利用获得的线性滤波器及新学习律对系统进行后续批次迭代，直到满足收敛条件为止。仿真显示：在针对输出误差二范数这个性能指标，该方法与小波滤波相比，降低了近15%，并消除了由于小波滤波阈值选取过小产生的振铃现象；在批次间噪声累积上，降低了9%左右。仿真结果表明，提出的等效滤波器综合设计方法，有效抑制了随机噪声的影响，并提高了系统跟踪的准确性。

迭代学习；随机噪声；无限脉冲响应(IIR)滤波器；小波变换；控制器优化

0 引言

迭代学习控制(Iterative Learning Control, ILC)适用于具有重复运动性质的被控对象，可实现有限时间区间内的完全跟踪[1]。ILC是在输入信号具有可重复性的前提下执行的，然而在实际的工业过程中总是不可避免地存在不确定干扰或随机噪声扰动，使系统不能实现完全跟踪，严重破坏了系统的控制品质。目前针对迭代学习控制系统中存在随机噪声扰动问题，文献[2-3]提出一种基于信号处理的滤波方法减小控制系统中随机噪声的影响；文献[4]提出了基于改进扩展状态观测器(Extended State Observer， ESO)估计的P型迭代学习控制算法，并利用干扰补偿增益实现干扰从输出中衰减的效果；文献[5]通过对误差中随机部分的分析，从控制器设计的角度出发，设计了最优内部反馈控制器并对迭代学习控制器进行了优化，在一定程度上降低系统的随机噪声产生的影响。上述文献提出的方法，能够在一定程度上消除随机噪声扰动的影响，但都是将控制器设计与滤波方法独立开来解决迭代学习控制系统中的随机扰动问题，且只在设定的批次时获得较好的控制性能，随着迭代次数的增加，随机噪声在批次间叠加使得迭代学习的效果越来越差，严重影响了产品品质。

本文提出一种滤波器与控制器设计相结合的ILC优化设计方法，以解决迭代学习控制系统中的随机扰动问题。本文主要针对单输入单输出 (Single Input Single Output， SISO)的线性时不变离散系统，通过对系统模型设计获得最优内部反馈控制器，并应用文献[6]中提出的基于小波变换的二次实验滤波法对系统的误差信号进行滤波处理，使系统的性能获得了一定程度的改善。但由于基于小波变换的滤波并不能获得明确的解析表达式，无法进一步对迭代学习控制器进行分析设计。所以本文又进一步提出了无限脉冲响应(Infinite Impulse Response, IIR)数字滤波器等效小波滤波的迭代学习控制器优化方案，提高迭代学习控制系统抗随机扰动性能。通过计算和比较不同方法下系统输出误差二范数值随迭代批次增加时的变化情况，进一步说明本文算法的有效性。

1 系统描述

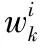
(1)

由图1可得到第i次迭代的输出为：

(2)

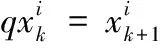
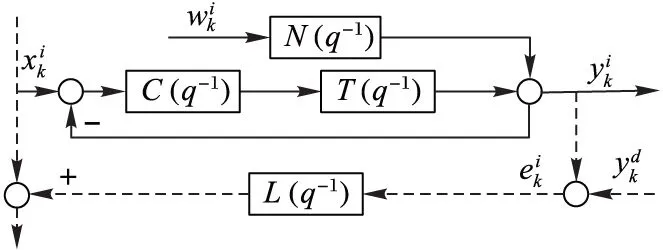
图1 随机噪声输入迭代学习控制系统

2 系统控制器设计

根据图1给出的系统模型，可得到第i次迭代后的输出误差表达式为：

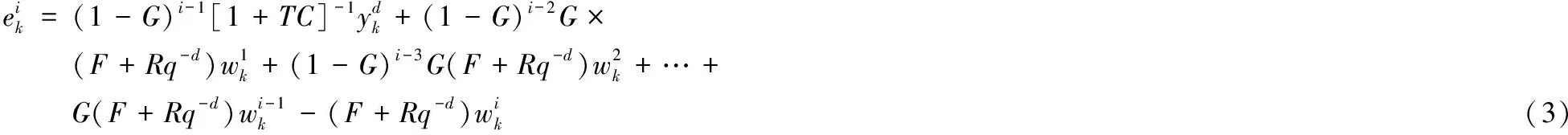
其中F+Rq-d=(1+TC)-1N由丢番图方程[7]分解得到；由式(3)可以看出G=1时系统输出误差最小，即迭代学习控制器为系统的逆，而实际过程中由于系统的非最小相位问题等导致系统的逆并不存在，此时系统的控制器设计即为求解最优的控制器C和L的参数问题。由于对控制器的联合设计是一个复杂的非线性规划问题无法获得全局最优解，因此本文应用依次设计内部反馈控制器与外部迭代学习设计控制的方法。

2.1 内部控制器的设计

由式(3)可以看出系统的输出误差由两部分组成，由参考输入产生的确定性误差：

由随机噪声产生的非重复误差：

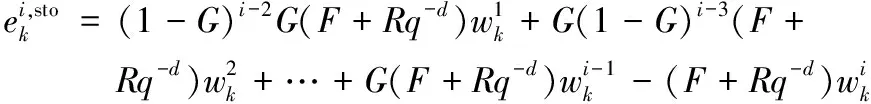
由丢番图方程可以看出F为内部反馈控制器的独立项，R为其余项。因此系统内部反馈控制器参数可以通过改变随机误差表达式中的R项来获取，从而得到最优的内部反馈控制器。根据图1可以得到系统第i次随机扰动输出为：

(4)

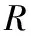
(5)

根据式(5)可以得到输出方差表达式为：

由式(6)的表达形式可以得到使得随机噪声输出影响最小且内部最优的反馈控制器：

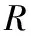
(7)

2.2 迭代学习控制器的设计

由式(3)可以看出，系统迭代学习控制器同时影响了迭代学习误差的重复部分与随机部分。因此最优迭代学习控制律参数的选取应满足以下两个要求：1)满足系统收敛性；2)使系统的输出误差不确定部分尽量小。由式(3)及式(7)可以得到式(8)：即获得内部最优反馈控制器后系统的误差表达式。

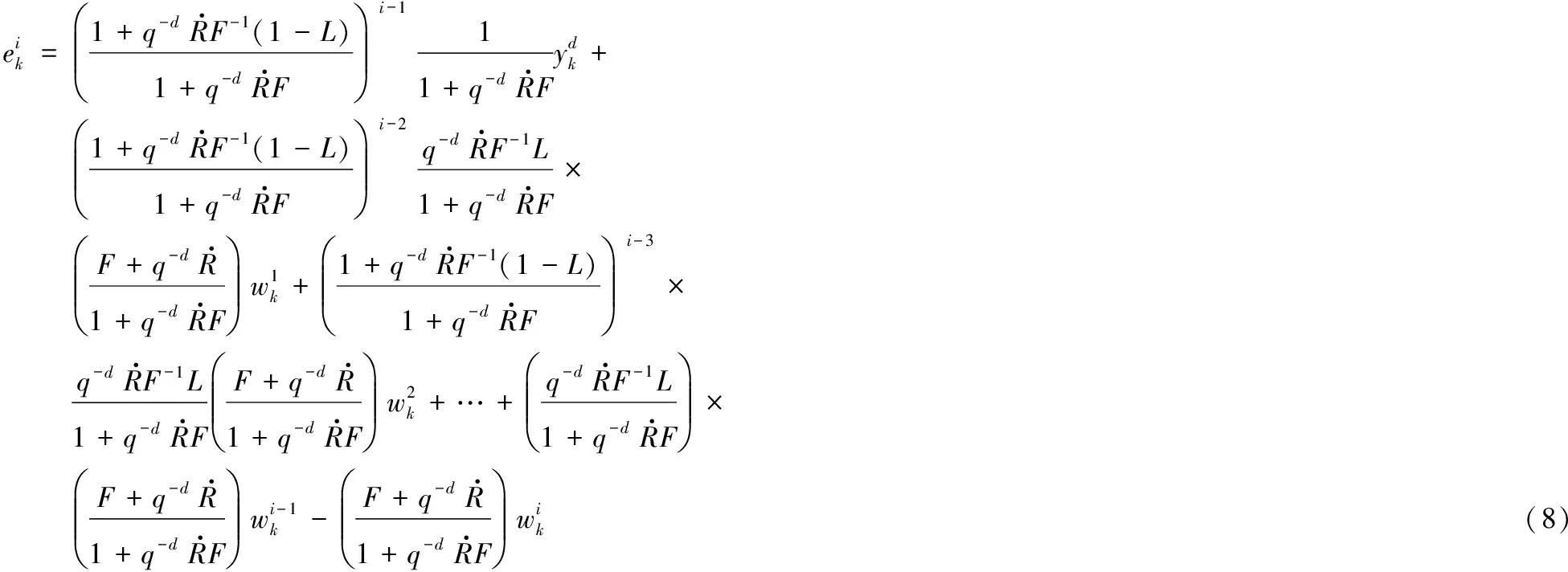
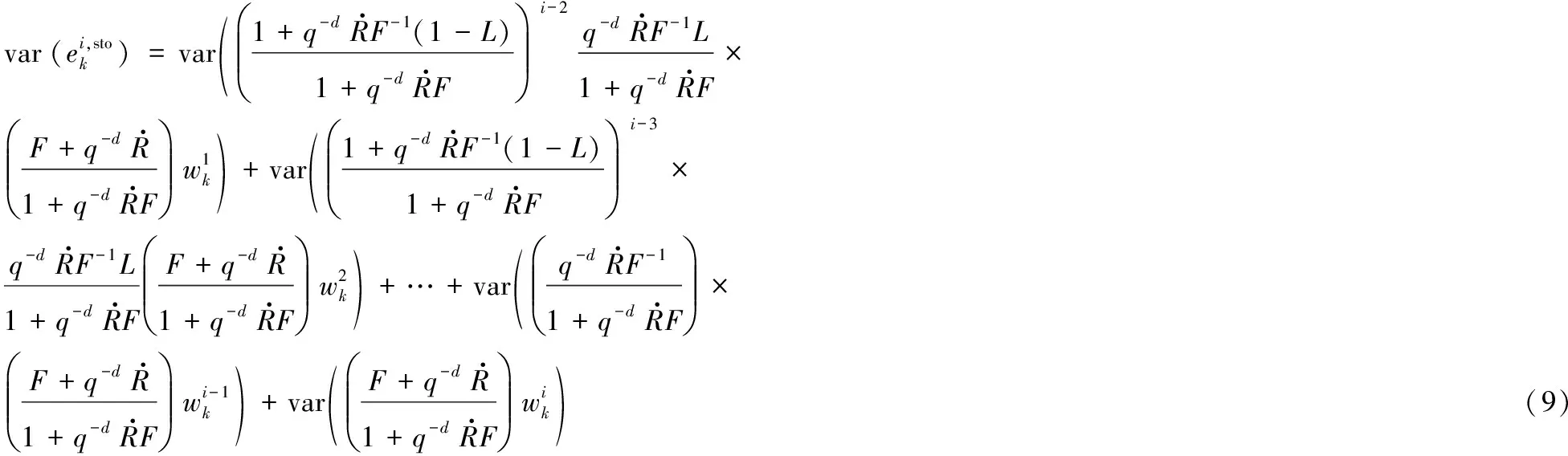
针对式(9)的优化问题，由文献[5]中定理1：

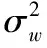
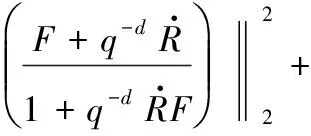
(10)

由式(10)可以看出该目标函数实质为输出误差二范数，其参数求解为凸优化问题[8]，可应用Matlab优化工具箱求解得到该批次的最优迭代学习控制器。

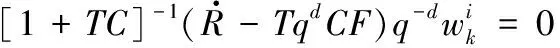
3 等效小波滤波的ILC控制器设计

3.1 二次实验法小波滤波

本节介绍一种基于离散小波变换[9]的二次实验算法，对于一个迭代批次中的误差信号，其重复部分经小波变换可获得相同的小波系数cr，非重复部分产生不同的小波系数cnr，将两次实验的小波系数的比较可以得到误差信号中的确定部分。通过小波变换的阈值选择获得一组有效小波系数，该系数用于重构滤波后误差信号，即对随机误差的滤波过程[10]。

其滤波的详细过程为：

c1=cr+cnr,1

(11)

c2=cr+cnr,2

(12)

其中下标表示的是一次迭代的两次实验序号，并不表示不同的迭代批次。将式(11)～(12)得到其只包含误差非重复部分的小波系数：

Δc=c1-c2=cnr,1-cnr,2

式(11)+(12)可得：

选取有效小波系数：

(13)

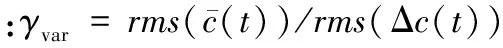
由文献[11]可知基于小波变换的滤波并不影响系统的稳定性。基于小波变换的滤波能够进一步地减小随机噪声扰动对迭代学习控制系统的影响，但其也存在以下缺点，基于小波变换的信号滤波过程不能获得明确的解析表达式，进而无法获得输出误差表达式，因此无法设计外部控制器，且每个迭代批次都需要实验两次，同时小波变换阈值选取过程复杂，过小会产生跳变振铃现象，过大则滤波效果不理想[12]。因此本文进一步提出用IIR型数字滤波器逼近二次实验法小波滤波的ILC控制器优化设计的方法。

3.2 基于IIR滤波器的迭代学习控制器设计

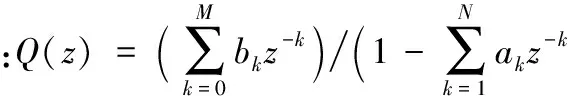
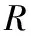
由于对输出误差实施了滤波处理，滤波后的误差输出已尽量平稳，此时可选择P型迭代学习控制律。其优化过程见2.2节。

总结以上的分析设计过程，下面给出了系统设计的完整流程，如图2所示。

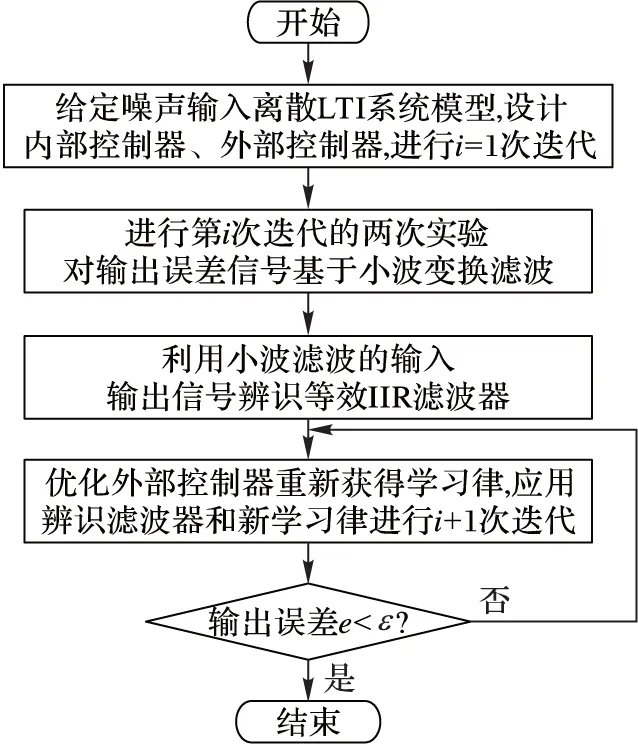
图2 系统设计方案流程

4 设计与仿真

针对第2章所描述问题为了验证本文提出方法的效果，本章给出了具体的仿真实验，其系统框图如图3所示。

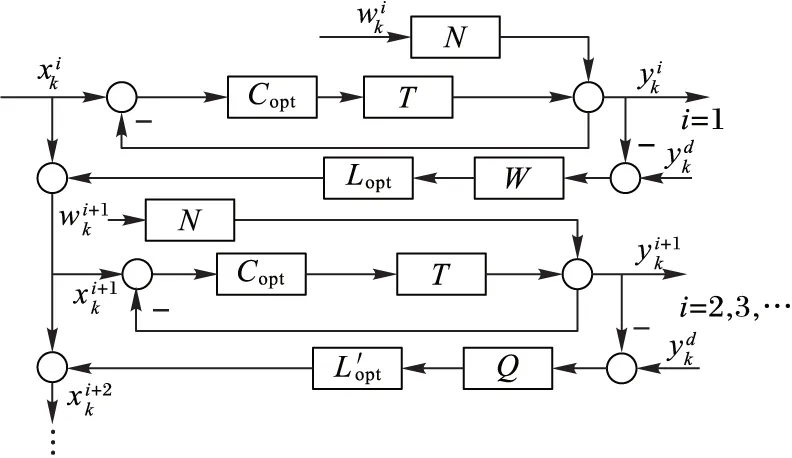
图3 基于本文控制器的系统框图

例1 针对有色噪声输入的系统模型为：T=(0.9q-2-0.6q-3)/(1-0.7q-1)，噪声模型为：N=(1-0.2q-1)/(1-0.9q-1)，并设定期望输入为正弦函数。可以求得系统内部最小方差控制器为：Copt=(0.21-0.147q-1)/(0.3-0.29q-1-0.129q-2+0.126q-3)及基于噪声扰动下的优化外部迭代学习律的控制器为：Lopt=(0.789q2-0.118q-0.007 8)/(0.63(1+0.143q-1))，应用三层小波分解综合滤波器W，辨识的等效线性滤波器为：

Q(q-1)=(0.001 98+0.003 9q-1+0.002 9q-2+ 0.000 95q-3+0.000 117q-4)/(1+0.572z-1+ 0.122 7z-2+0.011 7q-3+0.000 42q-4)

重新优化的P型迭代学习控制律为：Lopt′ = 0.012 4，对系统分别实施2次迭代、12次迭代输出曲线如图4(a)、4(b)所示。

由图4(a)的系统输出曲线对比可以看出，对系统施加基于小波变换的滤波处理，可以进一步地消除随机噪声的影响，但是系统输出在0.1s、5.7s及6.7s附近分别产生了振荡现象。基于等效滤波器的控制器优化设计在同样减小随机噪声的影响的同时，又进一步消除由于小波变换阈值选取过小产生的振铃抖动现象。

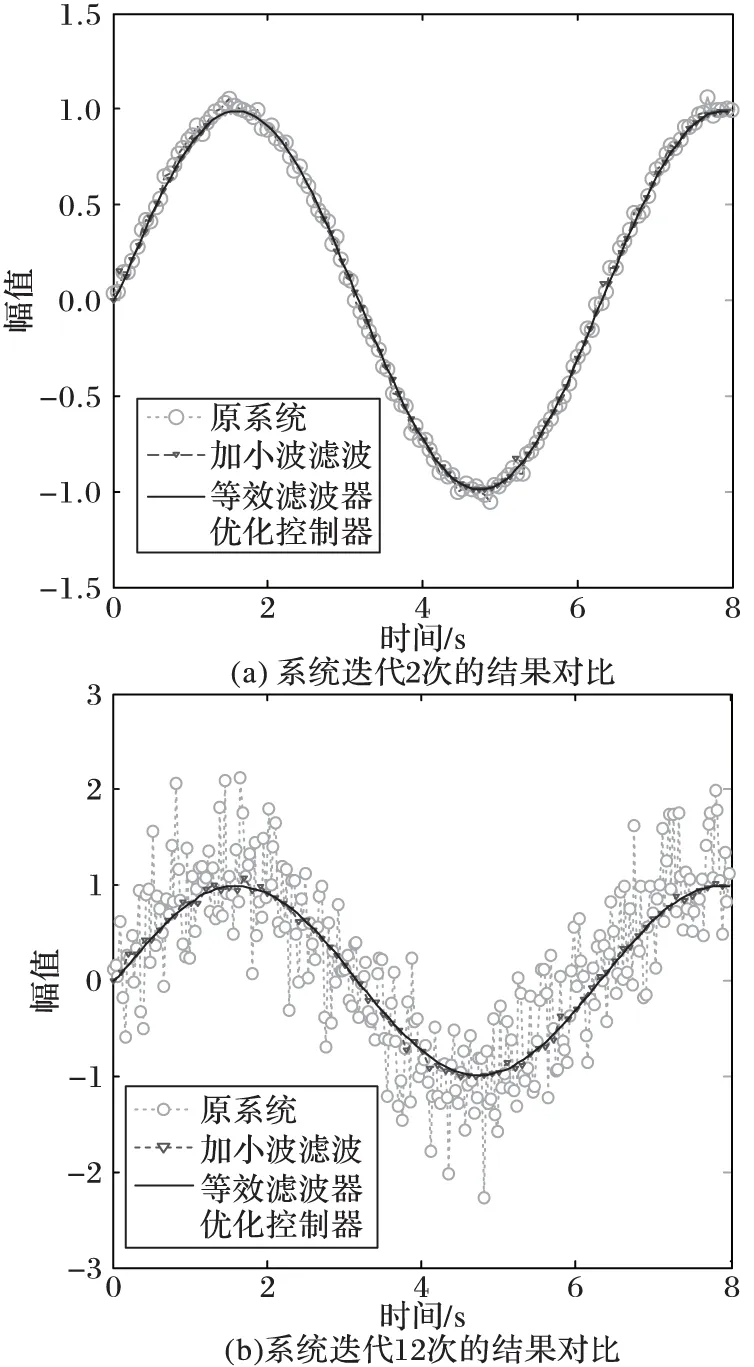
图4 系统不同迭代次数结果对比

由图4(b)的对比可以看出，原系统中噪声随迭代次数的增加产生了严重的累积现象。针对误差二范数值的指标，在第12个批次内，原系统为28.01，基于小波变换的滤波为2.65，结合等效滤波器的迭代学习控制器设计方法为0.540 5；本文较小波滤波方法提高了约7.5%；在批次间，由第2次到第12个批次的过程，原系统误差二范数值增加了27.23，基于小波变换的滤波方法误差二范数增加了2.1，而等效滤波器的优化控制器方法下误差二范数的值增加了0.018 9。本文较小波滤波方法提高了约7.7%。为进一步说明结合滤波器的迭代学习控制器设计方法的有效性，此部分给出了迭代次数与系统输出误差二范数的关系曲线以及部分迭代批次下系统输出误差二范数值，分别如图5和表1所示。

由图5、表1可以看出，基于等效滤波器的迭代学习控制器优化设计，相较只应用基于小波变换的滤波方法，能够更好地消除随着迭代批次增加而累积的噪声，提高了控制系统抗随机扰动的性能。

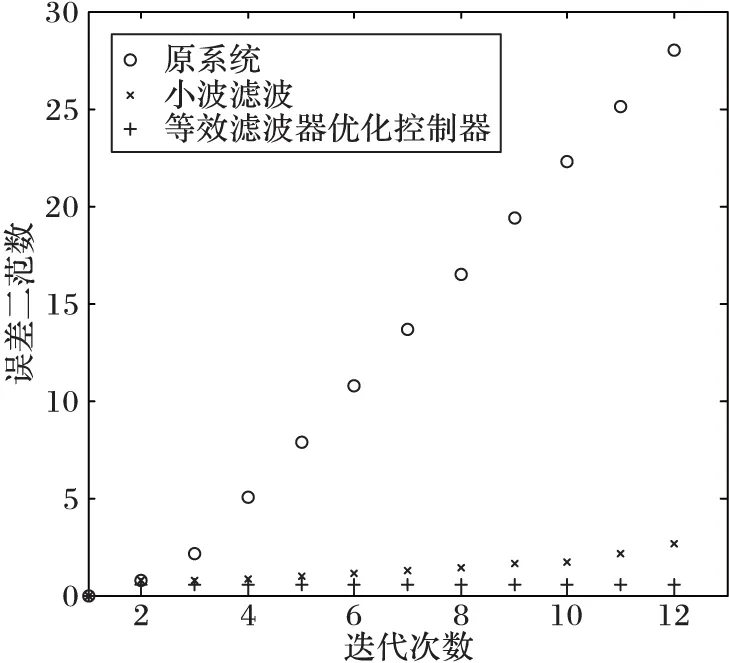
图5 迭代次数与误差二范数关系

5 结语

本文提出了一种滤波器与ILC控制器结合的优化设计算法，该算法应用基于二次实验小波变换滤波下的误差输入输出辨识出等效的线性数字滤波器，并且进一步优化迭代学习控制器。该算法与只基于小波变换的滤波相比，克服了小波滤波产生的振铃现象，并且充分减小了批次过程的噪声过分累积情况。本文也存在一定的不足，由于基于小波变换的滤波效果与其阈值选取有关，而线性滤波器的获取是由小波滤波的输出辨识得到，本文阈值选取范围凭借经验，具有一定主观性。因此，是否可以建立线性滤波器系数与小波变换阈值的数学关系也是进一步的研究方向。

)

[1] 孙明轩,严求真.迭代学习控制系统的误差跟踪设计方法[J].自动化学报,2013,39(3):251-262.(SUNMX,YANQZ.Errortrackingiterativelearningcontrolsystemdesign[J].ActaAutomaticaSinica, 2013, 39(3): 251-262.)

[2]TSAIMS,LINMT,YAUHT.Developmentofcommand-basediterativelearningcontrolalgorithmwithconsiderationoffriction,disturbance,andnoiseeffects[J].IEEETransactionsonControlSystemsTechnology, 2006, 14(3): 511-518.

[3]YEY,TAYEBIA,LIUX.All-passfilteringiniterativelearningcontrol[J].Automatica, 2009, 45(1): 257-264.

[4]SUNJ,LIS,YANGJ.Iterativelearningcontrolwithextendedstateobserverforiteration-varyingdisturbancerejection[C]//Proceedingsofthe2014 11thWorldCongressonIntelligentControlandAutomation.Piscataway,NJ:IEEE, 2014: 1148-1153.

[5]FARASATE,HUANGB.Deterministicvs.stochasticperformanceassessmentofiterativelearningcontrolforbatchprocesses[J].AIChEJournal, 2013, 59(2): 457-464.

[6]MERRYR,VANDEMOLENGRAFTR,STEINBUCHM.Theinfluenceofdisturbancesiniterativelearningcontrol[C]//CCA2005:Proceedingsof2005IEEEConferenceonControlApplications.Piscataway,NJ:IEEE, 2005: 974-979.

[7] ÅSTRÖMKJ,WITTENMARKB.Computer-ControlledSystems:TheoryandDesign[M].NorthChelmsford:CourierCorporation, 2013: 145-162.

[8] 邵言剑,陶卿,姜纪远.一种求解强凸优化问题的最优随机算法[J].软件学报,2014,25(9):2160-2171.(SHAOYJ,TAOQ,JIANGJY.Stochasticalgorithmwithoptimalconvergencerateforstronglyconvexoptimizationproblems[J].JournalofSoftware, 2014, 25(9): 2160-2171.)

[9]KARAMS,TETIR.Wavelettransformfeatureextractionforchipformrecognitionduringcarbonsteelturning[J].ProcediaCIRP, 2013, 12: 97-102.

[10]TORRENCEC,COMPOGP.Apracticalguidetowaveletanalysis[J].BulletinoftheAmericanMeteorologicalSociety, 1998, 79(1): 61-78.

[11]DAUBECHIESI.Thewavelettransform,time-frequencylocalizationandsignalanalysis[J].IEEETransactionsonInformationTheory, 1990, 36(5): 961-1005.

[12]ELLMAUTHALERA,PAGLIARICL,DASILVAEAB.Multiscaleimagefusionusingtheundecimatedwavelettransformwithspectralfactorizationandnonorthogonalfilterbanks[J].IEEETransactionsonImageProcessing, 2013, 22(3): 1005-1017.

[13]STORNR.DifferentialevolutiondesignofanIIR-filter[C]//Proceedingsof1996IEEEInternationalConferenceonEvolutionaryComputation.Piscataway,NJ:IEEE, 1996: 268-273.

[14]LIUT,YAOK,GAOF.Identificationandautotuningoftemperature-controlsystemwithapplicationtoinjectionmolding[J].IEEETransactionsonControlSystemsTechnology, 2009, 17(6): 1282-1294.

ThisworkissupportedbytheNationalNaturalScienceFoundationofChina(61273098).

XIA Hao, born in 1971, Ph.D., professor.His research interests include controller performance assessment, advanced process control.

ZHANG Lijie, born in 1991, M.S.candidate.Her research interest include iterative learning control.

Design of iterative learning controller for systems with random noise

XIA Hao, ZHANG Lijie*

(CollegeofControlScienceandEngineering,DalianUniversityofTechnology,DalianLiaoning116023,China)

To reduce the negative impact of stochastic noise in iterative learning control system, an iterative learning controller design method based on the Infinite Impulse Response (IIR) digital filter was proposed.For the first batch, the output errors from two repeated experiments were filtered by wavelet transform.Then the input/output data during the wavelet filtering process were used to obtain an equivalent IIR filter, which would be used to reconstruct the error objective function and optimize the iterative learning controller.Finally, the obtained IIR filter was applied to filter out the stochastic noise from subsequent batches until the convergence condition was met.Through simulation, compared with wavelet filtering, it could be demonstrated that by applying the proposed method, the 2-norm of output error could be reduced by nearly 15% and the ringing caused by setting the wavelet filter threshold too small was also avoided.The cumulative noise between the batches could be reduced by about 9%.The simulation results show that the proposed algorithm not only significantly reduces the negative effect of stochastic noise, but also effectively improves the accuracy of the tracking system.

iterative learning; stochastic noise; Infinite Impulse Response (IIR) filter; wavelet transform; controller optimization

2016-08-14;

2016-09-07。 基金项目:国家自然科学基金资助项目(61273098)。

夏浩(1971—)，男，黑龙江哈尔滨人，教授，博士，主要研究方向：控制器性能评价、先进过程控制； 张丽杰(1991—)，女，吉林长春人，硕士研究生，主要研究方向：迭代学习控制。

1001-9081(2017)01-0294-05DOI:10.11772/j.issn.1001-9081.2017.01.0294

TP273.22;TP

A