基于压缩感知的无线传感器网络动态采样方法
2017-04-17黄志清张严心李梦佳
宋 洋,黄志清,张严心,李梦佳
(1.北京工业大学 软件学院,北京 100020; 2.北京市物联网软件与系统工程技术研究中心,北京 100020;3.北京交通大学 电子信息工程学院,北京 100044)
(*通信作者电子邮箱zqhuang@bjut.edu.cn)
基于压缩感知的无线传感器网络动态采样方法
宋 洋1,2,黄志清1,2*,张严心3,李梦佳1,2
(1.北京工业大学 软件学院,北京 100020; 2.北京市物联网软件与系统工程技术研究中心,北京 100020;3.北京交通大学 电子信息工程学院,北京 100044)
(*通信作者电子邮箱zqhuang@bjut.edu.cn)
基于固定采样率的无线传感网(WSN)压缩感知(CS)在收集随时间变化的数据时难以获得满意的数据恢复精度。针对该问题,提出了一种基于数据预测和采样率反馈控制的动态采样方法。首先,汇聚节点通过分析当前采样时段与上一采样时段获取数据的线性度量指标,预测数据的变化趋势;然后,根据预测结果计算感知节点未来的采样率,并通过反馈控制机制对感知节点的采样过程进行动态调节。实验结果表明,相比基于目前广泛采用的基于固定采样率的无线传感网压缩感知数据收集方法,该方法能够有效提高压缩数据的恢复精度。
无线传感器网络;压缩感知;数据预测;反馈控制;动态采样
0 引言
目前,无线传感器网络(Wireless Sensor Network, WSN)[1]已经被广泛用于各个领域中[2-3]。由于传感器节点通常由电池供电,并且通常没有持续的电力供应,所以如何节省能耗是无线传感器网络应用过程中需要解决的核心问题。针对该问题,一些学者将压缩感知(Compressive Sensing, CS)理论[4-5]应用于网络的数据收集过程中[6-9],利用被收集的数据的时空相关性,将数据稀疏化表示,通过节点的随机采样,从少量的数据样本中精确恢复出原始数据,达到降低感知节点的采样频率和数据传输量、延长寿命的目的。但是,上述研究成果大多假设被收集的数据稀疏特性不随时间动态变化,所以可以采用固定的采样率,准确地收集被测量数据。在实际场景中,当数据动态变化时,采用固定采样率进行采样可能使感知节点无法获取足够的原始数据特征信息,导致汇聚节点恢复的数据精度不理想。
目前,针对收集具有时间相关性数据过程中遇到的此类问题,已有一些学者提出了一些基于动态采样的探讨性方法。由于无法预先获取即将收集到的数据,所以这些方法大多通过对先验数据的分析,建立采样率与被收集数据某一特征的关联关系,从而在数据收集过程中,根据该特征的变化自动调节节点的采样率,达到降低数据获取的误差和节省能耗的目的。例如:文献[10]将节点数据收集的过程分为等长的时间段,通过分析历史数据特点确定每个时段的采样率,使节点的采样过程可以根据当下所处的时段切换到对应的采样率;文献[11-12]通过对历史数据的分析得到数据获取误差的可接受阈值,在数据收集阶段通过比较获取到的数据误差是否满足该阈值,对节点进行采样率反馈控制;文献[13]首先使节点进行密集采样,获得原始数据,通过分析原始数据建立数据的稀疏度与采样率的哈希表,每轮数据收集完成后通过分析数据的稀疏度,检索后续采样对应的采样率。综上所述,目前研究成果主要可以用图1进行概括。
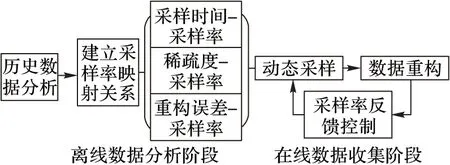
图1 相关研究的采样率动态调整流程
本文针对此类问题提出了一种新颖的动态采样调度方法,该方法通过预测数据的变化趋势动态调整节点的采样率,省略了上述方法中历史数据分析和采样映射关系的建立过程,简化了数据压缩收集的流程。在数据收集的开始阶段,感知节点实时地进行数据的压缩收集,而后将采收集的样本数发送给汇聚节点,汇聚节点对收集到的样本数据解压后进行线性拟合,通过对比当前采样时段和上一采样时段重构数据的线性程度量指标的差异,获取得到被观测数据的变化趋势。然后,汇聚节点根据该变化趋势预测下一轮压缩感知需要的采样频率,并通过采样率反馈控制架构对网络内节点的采样过程进行动态调节。
1 基于压缩感知的采样调度方法建模
在使用无线传感器节点进行数据收集过程中,受到节点硬件对采样频率的制约,采集到的数据通常是离散数据,所以本文选用离散时间模型对无线传感器网络中感知节点的时域采样问题进行建模[14]。
在无线传感器网络中,某个节点一段时间采集到的时序物理量可以用X={Xt}(t=1,2,…,N)表示。其中:t表示时间序列的时刻,N表示所有的采样时刻。令无线传感器节点的对物理量的采样策略用π表示,采用该策略进行采样,采样的时刻可以表示为:
Tπ=(t1,t2,…,tn);ti∈{1,2,…,N},1≤i≤n
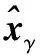
如果将压缩感知方法应用到无线传感器网络的数据收集过程中,那么可以上述数据的收集过程可以描述为:对于一个时间序列长度为N离散环境数据x,感知节点采用采样调度策略Tπ进行了M次重复采样,这些采样时间点组成了一个M×N的观测矩阵Φ。在矩阵Φ的构造过程中,矩阵的行数M表示总共需要采样的次数,列数N表示被采集数据的时间长度,当矩阵的(m,n)元素为1时,代表第m次采样发生在第n时刻,由此可以看出矩阵Φ实际代表了一组对信号x的收集策略。采用Φ对x经过M次观测后得到一个维的观测值xπ=y:
y=Φx
如果x是可压缩信号,即存在一个M×N的矩阵Ψ,使x可以在表示域Ψ内被稀疏表示,那么x可以被描述为:
x=Ψs
其中:s是N×1的稀疏向量,‖s‖1=K,且K≤N。则矩阵Ψ为稀疏表示基,那么观测值向量y可以表示为:
y=ΦΨs
对于矩阵Φ,如果M满足M≥Cμ2(Φ,Ψ)KlgN,则通过重构过程
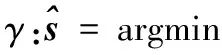
s.t.y=ΦΨs
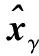
2 基于数据预测的动态采样调度方法
当被收集数据随时间动态变化,其内部的稀疏化特征可能也会随之改变。如果数据的稀疏度改变(即K改变),就需要动态地调整观测矩阵的维度M,使收集到的观测样本数量能够满足精确重构数据的条件。该过程实质就需要设计一种动态采样调度策略π,使感知节点根据稀疏度的变化动态调整收集样本的数量。
在分析数据的稀疏度时,如果被收集的信号随着时间变化而发生线性变化,那么就可以找到特定的稀疏基Ψ使这个信号获得良好的稀疏化表示,从而使汇聚节点可以通过感知较少的观测样本精确重构出原始信号。为了计算数据的线性程度,本文采用线性拟合决定系数R2作为评价指标。R2通常被用来评价线性拟合结果与回归直线的拟合程度,其取值范围为0~1,当R2越接近1时,说明数据之间的线性程度越好,反之则线性程度越差。
但是,真实环境中的各类数据的整体线性特征通常并不明显,这使得数据的稀疏化程度通常较差,只有在收集该数据的过程中采用较高的采样率,获得足够的局部特征,才能获得相对满意的数据重构误差。但是,如果将信号进行分段收集,那么某些局部数据可能具有较强的线性的特征,因此可以通过降低收集这些时段数据时节点的采样率,节省能耗;反之,对线性特征较弱的局部数据提高节点采样率,保证数据获取精度。由于现实场景中的各类数据会随时间的变化而缓慢变化,该过程一般是渐变的并且具有一定的趋势特征,所以可以利用数据变化的趋势预估未来一段时间内的变化情况。
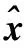
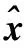
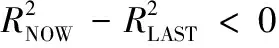
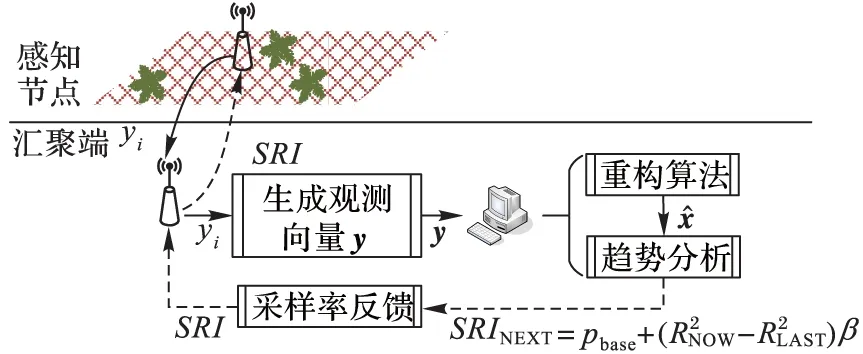
图2 基于数据预测的动态采样调度方法流程
另外,采样时长N决定了被收集的原始数据的长度。为了降低感知节点与汇聚节点的进行同步时的数据量,本文采用等时长分段采样策略,即每个采样时段的被收集信号长度N均相同,在此基础上本文提出的动态采样调度算法如下。
算法 基于数据预测的动态采样调度算法。
Input:基础准采样率pbase,观测值y,稀疏表示基Ψ。Output:重构数据,下一轮采样率指标SRINEXT。
1)
Φ←0
/*初始化观测矩阵*/
2)
将当前基准采样率pbase广播给传感节点;
3)
fori=1toMdo
4)
Ω←{jthejth received value};
/*记录收到的观测数据*/
5)
endfor
6)
forj=1 toNdo
7)
ifj∈Ω&&Ω>0then
8)
Φ(i,j)←1;
/*构造观测矩阵*/
9)
endif
10)
endfor
11)
θ=Φ×Ψ;
12)
s.t.θs=y;
/*重构信号*/
13)
/*重构原始信号*/
14)
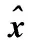
15)
if本轮为首次压缩感知 /*计算2轮压缩感知的动态采样率*/
16)
SRINEXT=pbase+(1-R2NOW)β;
17)
else/*计算余下压缩感知过程的动态采样率*/
18)
SRINEXT=pbase+(R2NOW-R2LAST)β;
19)
endif
20)
将下一次采样率SRINEXT反馈给采样节点;
其中,感知节点在数据收集的起始阶段采用基准采样率pbase进行采样。在后续的采样时段中,各个分段的采样率根据每段重构数据的线性程度不同而围绕pbase上下波动。
2.1 实验数据
本文通过部署在北京工业大学内的CrossbowMICAz环境监测无线传感器网络收集校内特定区域内的全天的温度数据,网络内的MICAz节点以2min/次的采样间隔进行周期性采样。本文选取了网络内某一节点收集到的温度数据作为实验数据,该数据如图3所示。

图3 原始温度数据
2.2 观测矩阵Φ
如本文第1章所描述的,观测矩阵中的非零元素位置代表了节点采样的时刻。如果采用随机采样方案,那么如何使汇聚节获知感知节点的采样时刻也是需要解决关键的问题。所以,为了降低方案实施的难度,本文中采用周期性采样方法,对应的观测矩阵形式如下:

观测矩阵每行只有1个非0元素,非0元所在列代表采样时刻,每行的非0元素的间隔相同,矩阵中列与列的间隔代表了原始数据中相邻数据点的时间间隔,即2min。
2.3 稀疏基Ψ与数据稀疏化分析
为了验证实验数据能否被稀疏化表示,本文对图3的温度数据采用快速傅里叶变换(FastFourierTransform,FFT),得到的结果如图4所示。

图4 快速傅里叶变换系数
结果显示实验数据的稀疏度近似为K=52≪720,所以该温度数据可以认为是可压缩数据。所以采用快速傅里叶变换(FFT)基作为稀疏表示基Ψ。
2.4 重构算法
目前,在研究领域中诸如MP(MatchingPursuit)、OMP(OrthogonalMatchingPursuit)、BP(BasisPursuit)等诸多重构算法及改进算法被提出。在实际应用中,有第三方组织发布的诸如CVX、spams等稀疏化工具箱,提供了数据恢复算法的API(ApplicationProgrammingInterface)。虽然采用不同算法在数据重构时的计算复杂度和数据恢复精度各不相同,但是目前的研究尚且没有证明那种重构可以获得最优效果。所以,为了简化实验过程,本文实验采用CVX工具箱提供的优化算法作为重构算法[15]。
2.5 能量模型
为了评价节点在数据收集过程中能量消耗,本文采用了比特跳能量模型[16],该能量模型如下:
其中:ETx(l,d)表示将l比特的数据传输距离为d的能量消耗,ERx(l)表示节点接收l比特数据消耗的能量,Eelec表示发送或者接收1比特数据包所消耗的能量,εamp表示传输放大功率。在本文的后续实验中,取Eelec=50 nJ/bit,εamp=100 pJ/bit/m2,数据包长度为1 024 b,节点的初始能量为50 J,数据的传输距离为50 m。由于节点的数据通信能耗远大于采样和指令处理产生的能耗,因此为了简化实验过程,本文忽略了数据收集过程中指令处理消耗的能量。
2.6 实验及结果分析
为了研究不同分段长度对于数据重构精度的影响,实验中分别采用数据段长度为N={30,60,120,180,360,720}进行数据收集实验。它们分别对应的采样时段长度为1,2,4,6,12,24 h,并且在实验开始阶段,本文将基准采样率设定为pbase=10%,影响因子设定β设为0.05。
首先,本文对不同分段的重构数据进行线性拟合,分析不同分段的线性程度(图5),然后通过基于数据预测的动态采样调度算法计算在不同数据分段情况下各个分段的动态采样率(图6),分析采样率与重构数据线性度量指标的关系。
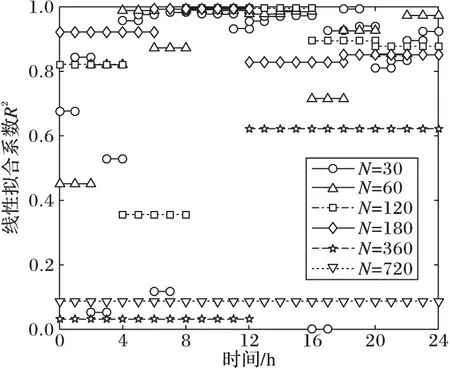
图5 不同分段长度的各段重构数据线性拟合优度
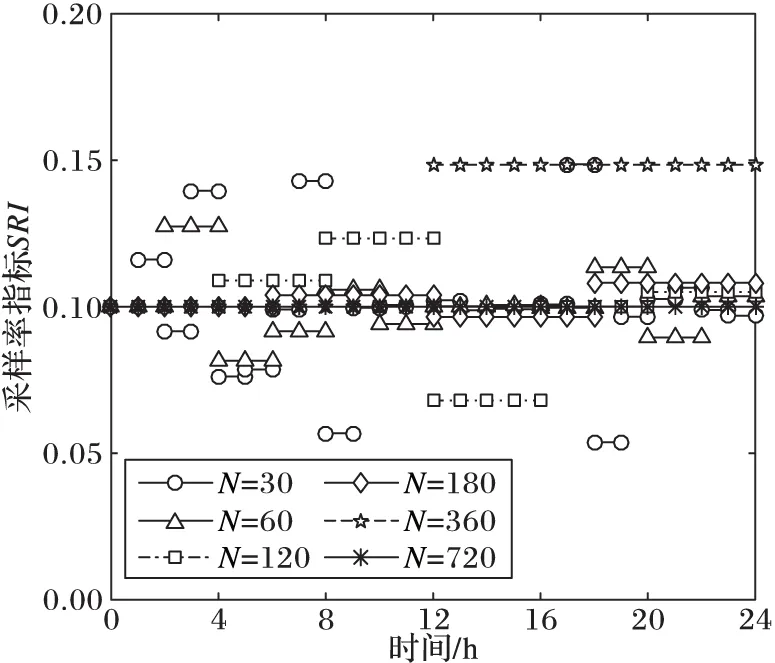
图6 不同分段长度的各数据段动态采样率
图5为不同分段长度下各个重构数据分段的线性拟合系数,从结果中可以发现前后两个采样时段重构数的线性度量指标R2下降快的有N=30时的第2段与第3段,第5段与第6段,第15段与第16段;N=60时的第3段和第5段以及N=120时的第1段与第2段。从图6的实验结果中也可以看到,上述各段随后的数据段的动态采样率都在15%左右,远高于基准采样率10%。另外,诸如N=30时的第6段与第7段,16段与17段等,线性程度大幅增强时,节点在后续的采样过程中会采用相对较低的采样率进行采样。综上所述,节点在未来时段的采样会跟随当前数据的线性程度的变化趋势进行自适应的调整,当重构数据线性程度增强时,节点会降低采样率,节省能耗;而当重构数据的线性程度减弱时,节点会相应地提高未来时段的采样率,以保证在该变化趋势下,准确地获取数据。
为了验证基于数据预测的动态采样方法在获取精度方面的优势,本文将该方法与采用固定采样率进行数据压缩采集的方法在数据获取误差上进行对比。实验中采用的误差评价指标如下:
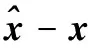
实验中,分别将两种数据收集方式的基准采样率为pbase=10%、pbase=20%和pbase=30%,令采样过程中的分段长度为N={30,60,120,180,360},在每种条件下重复采样和重构50次,得到的采用固定采样率和动态采样率设计的压缩感知观测矩阵的数据重构误差结果如图7所示。从实验结果中可以发现,两种数据获取方法在较高的基准采样率(pbase=30%)时数据的重构误差较低。在不同的基准采样率下,本文方法均能够一定程度地降低重构数据的误差。
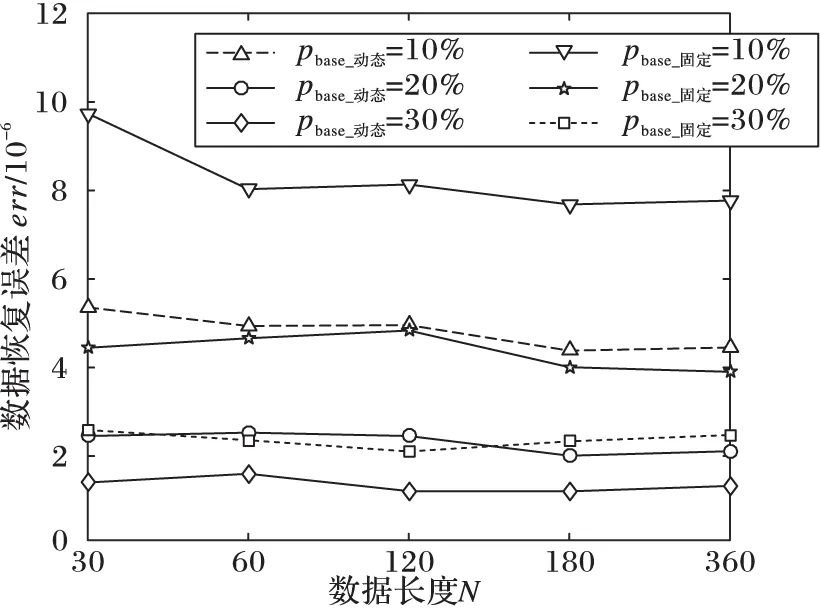
图7 固定采样率与动态采样率数据重建质量比较
另外,从实验结果中可以注意到,随着基准采样率的成倍增加,数据的误差并不会以相应的倍数降低,这主要是数据内的噪声(不可以被稀疏化的部分)对重构数据的影响造成的。因此在实际应用过程中,应该根据实际数据收集效果,选择适当的基准采样率。在使用同一采样方法进行采样时,在重建误差差距不大的情况下,应该尽可能选用较小的分段以减少重构计算的计算复杂度:当采用10%的采样率进行采样时,可以采用较大的数据段长度(如:N=360);而采用相对较大的基准采样率进行采样时,可以选用相对较短的数据段长度。
图8为基准采样率pbase=30%,数据段长度N=180的条件下,采用本文提出动态采样方法进行连续5天的数据压缩收集和重构获得的数据与原始数据的对比结果。从实验结果可以发现,重构数据的偏差多发生在原始数据波动性增加的时段,即数据线性程度较差的时段,在后续的采样过程中汇聚节点会调整采样节点的采样率使得采样节点采集更多的观测数据,使后续采样阶段的数据重构精度得到有效保证。
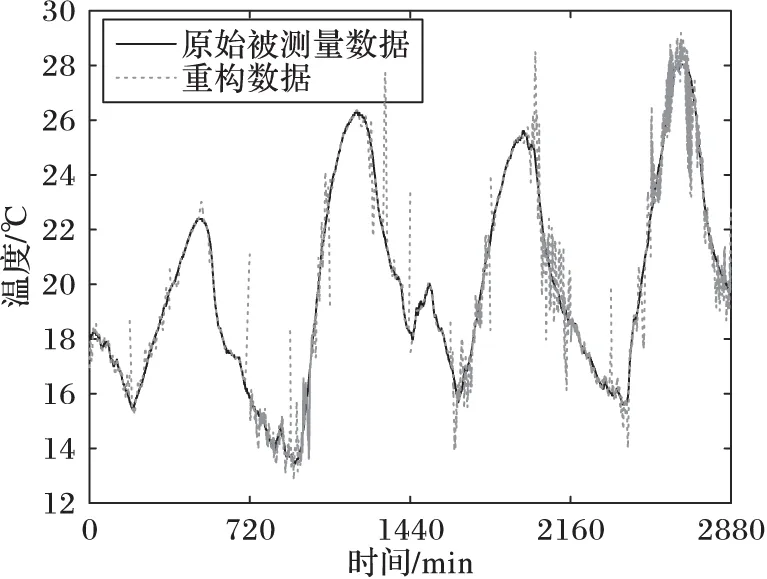
图8 N=180原始温度数据和重构温度数据
图9为在不同基准采样率下采用固定采样率方法和本文提出的动态采样方法在分段长度为N=180的情况下连续4天采样的能耗对比结果。在采用固定采样率的压缩感知数据采样过程中,由于每轮观测采样的数量和数据传输的数量是固定的,所以节点剩余能量的下降速度也是恒定的。相比之下,得益于数据预测和采样率的动态调节机制,本文方法能够在一定程度上降低节点的能耗速度,延长节点的寿命。
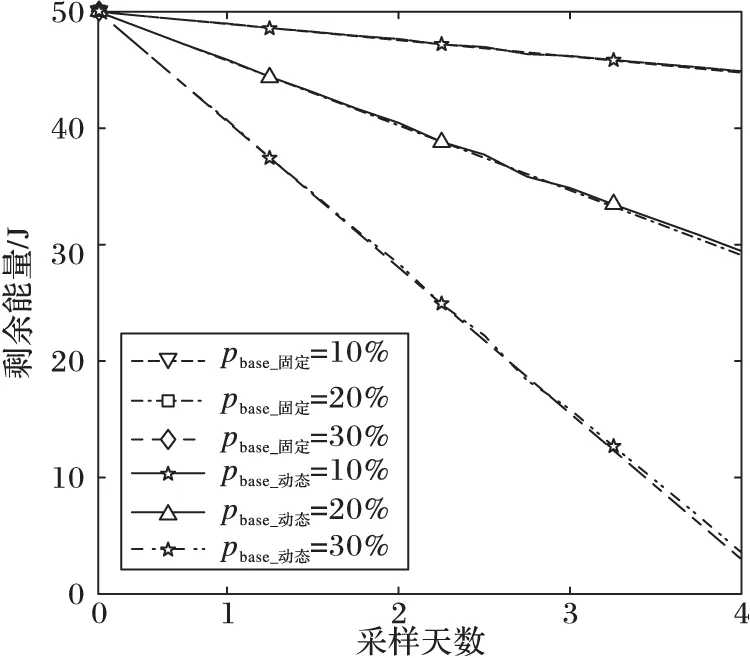
图9 N=180固定采样和动态采样能耗比较
3 结语
针对基于压缩感知无线传感器网络数据收集过程中,被收集数据随时间动态变化时,采用固定采样率的方法很难使节点准确地获取数据内一些动态变化的特征,使得数据恢复误差较大的问题,本文提出了一种新颖的动态采样方法。不同于已有方法,汇聚节点通过预测数据变化趋势计算合适的采样率,然后通过采样率反馈控制架构感知节点进行动态调节,从而简化了节点的动态采样的流程。经实验证明,相比使用固定采样率的方法,本文提出的方法能够使感知节点跟随数据的变化趋势动态调节合适的采样率,有效地降低了数据获取的误差,并且该方法在能耗上也具有一定的优势。
References)
[1] AKYILDIZ L F, SU W L.A survey on sensor networks [J].IEEE Communications Magazine, 2002, 40(8): 102-114.
[2] LIU Y, HE Y, LI M, et al.Does wireless sensor network scale? a measurement study on GreenOrbs [J].IEEE Transactions on Parallel & Distributed Systems, 2013, 24(10):1983-1993.
[3] MAO X, MIAO X, HE Y, et al.CitySee: urban CO2monitoring with sensors [C]// Proceedings of the 32nd IEEE International Conference on Computer Communications.Piscataway, NJ: IEEE, 2012: 1611-1619.
[4] DONOHO D L.Compressed sensing [J].IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306.
[5] CANDES E, ROMBERG J, TAO T.Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information [J].IEEE Transactions on Information Theory, 2006, 52(2): 489-509.
[6] WU X, WANG Q, LIU M.In-situ soil moisture sensing: measurement scheduling and estimation using sparse sampling [J].ACM Transactions on Sensor Networks, 2012, 11(2): 1-11.
[7] LUO C, WU F, SUN J, et al.Compressive data gathering for large-scale wireless sensor networks [C]// Proceedings of the 15th Annual International Conference on Mobile Computing and Networking.New York: ACM, 2009: 145-156.
[8] WANG W, GAROFALAKIS M, RAMCHANDRAN K.Distributed sparse random projections for refinable approximation [C]// International Symposium on Information Processing in Sensor Networks.Piscataway, NJ: IEEE, 2007: 331-339.
[9] LEE S, PATTEM S, SATHIAMOORTHY M, et al.Spatially-localized compressed sensing and routing in multi-hop sensor networks [C]// GSN 2009: Proceedings of the Third International Conference on GeoSensor Networks.Berlin: Springer, 2009: 11-20.
[10] 王国英,江雨佳,莫路锋,等.基于压缩感知的土壤呼吸监测传感网动态采样调度策略[J].中国科学:信息科学,2013,43(10):1326-1341.(WANG G Y, JIANG Y J, MO L F, et al.Dynamic sampling scheduling policy for soil respiration monitoring sensor networks based on compressive sensing [J].SCIENCE CHINA: Information Sciences, 2013, 43(10): 1326-1341.)
[11] CHEN W, WASSELL I J.Energy efficient signal acquisition via compressive sensing in wireless sensor networks [C]// Proceedings of the 2011 International Symposium on Wireless and Pervasive Computing.Piscataway, NJ: IEEE, 2011:1-6.
[12] RADOVIC M, DUKNIC M, TASESKI J.Sensing, compression, and recovery for WSNs: sparse signal modeling and monitoring framework [J].IEEE Transactions on Wireless Communications, 2012, 11(10): 3447-3461.
[13] HAO J, ZHANG B, JIAO Z, et al.Adaptive compressive sensing based sample scheduling mechanism for wireless sensor networks [J].Pervasive & Mobile Computing, 2015, 22:113-125.
[14] WU X, LIU M.In-situ soil moisture sensing: measurement scheduling and estimation using compressive sensing[C]// Proceedings of the 11th International Conference on Information Processing in Sensor Networks.New York: ACM, 2012: 1-12.
[15] GRANT M, BOYD S.CVX: Matlab software for disciplined convex programming [EB/OL].[2016-04-10].http://cvxr.com/cvx/.
[16] HEINZELMAN W B, CHANDRAKASAN A P, BALAKRISHNAN H.An application-specific protocol architecture for wireless microsensor networks [J].IEEE Transactions on Wireless Communications, 2002, 1(4):660-670.
This work is partially supported by the Fundamental Research Funds for the Beijing University of Technology (025000514314004), the National Development and Reform Commission’s Project Item (Q5025001201502).
SONG Yang, born in 1990, M.S.candidate.His research interests include wireless sensor network, compressive sensing.
HUANG Zhiqing, born in 1970, Ph.D., associate professor.His research interests include wireless sensor network, Internet of things, software defined network.
ZHANG Yanxin, born in 1976, Ph.D., associate professor.Her research interests include wireless sensor network, complex network control, reliable control of complex system.
LI Mengjia, born in 1993, M.S.candidate.Her research interests include wireless sensor network, compressive sensing.
Dynamic sampling method for wireless sensor network based on compressive sensing
SONG Yang1,2, HUANG Zhiqing1,2*, ZHANG Yanxin3, LI Mengjia1,2
(1.SchoolofSoftwareEngineering,BeijingUniversityofTechnology,Beijing100020,China;2.BeijingEngineeringResearchCenterforIoTSoftwareandSystem,Beijing100020,China;3.SchoolofElectronicandInformationEngineering,BeijingJiaotongUniversity,Beijing100044,China)
It is hard to obtain a satisfactory reconstructive quality while compressing time-varying signals monitored by Wireless Sensor Network (WSN) using Compressive Sensing (CS), therefore a novel dynamic sampling method based on data prediction and sampling rate feedback control was proposed.Firstly, the sink node acquired the changing trend by analyzing the liner degree differences between current reconstructed data and last reconstructed data.Then the sink node calculated the suitable sampling rate according to the changing trend and fed back the result to sensors to dynamically adjust their sampling process.The experimental results show that the proposed dynamic sampling method can acquire higher reconstructed data accuracy than the CS data gathering method based on static sampling rate for WSN.
Wireless Sensor Network (WSN); Compressive Sensing (CS); data prediction; feedback control; dynamic sampling
2016-05-26;
2016-07-18。
北京工业大学基础研究基金资助项目(025000514314004);国家发改委项目子项(Q5025001201502)。
宋洋(1990—),男,北京人,硕士研究生,主要研究方向:无线传感器网络、压缩感知; 黄志清(1970—),男,四川自贡人,副教授,博士,主要研究方向:无线传感器网络、物联网、软件定义网络; 张严心(1976—),女,辽宁盘锦人,副教授,博士,主要研究方向:无线传感器网络、复杂网络控制、复杂系统可靠控制; 李梦佳(1993—),女,北京人,硕士研究生,主要研究方向:无线传感器网络、压缩感知。
1001-9081(2017)01-0183-05
10.11772/j.issn.1001-9081.2017.01.0183
TP212.9; TP393
A
