基于功率谱及有限穿越可视图的癫痫脑电信号分析算法

王若凡，刘 静，王 江，于海涛，曹亦宾

(1.天津职业技术师范大学 信息技术工程学院，天津 300222；2.唐山市工人医院 神经内科，河北 唐山 064300； 3.天津大学 电气与自动化工程学院，天津 300072)

(*通信作者电子邮箱m18522619839@163.com)

基于功率谱及有限穿越可视图的癫痫脑电信号分析算法

王若凡1，刘 静2，王 江3，于海涛3，曹亦宾2*

(1.天津职业技术师范大学 信息技术工程学院，天津 300222；2.唐山市工人医院 神经内科，河北 唐山 064300； 3.天津大学 电气与自动化工程学院，天津 300072)

(*通信作者电子邮箱m18522619839@163.com)

针对可视图(VG)算法存在噪声鲁棒性差的问题，提出一种改进的有限穿越可视图(LPVG)建网方法。该算法基于可视图(VG)算法的可视性准则，并设定有限穿越视距，将时间序列中满足条件的点连接起来，从而将时间序列映射为网络。首先，对LPVG算法进行性能分析；然后，将LPVG算法结合功率谱密度(PSD)算法应用到癫痫发作前、中、后脑电信号的识别上；最后，提取三种状态下癫痫脑电信号的LPVG网络特征参数，研究癫痫对网络拓扑结构的影响。仿真结果表明，与VG和水平穿越可视图(HVG)相比，虽然LPVG算法的时间复杂度较高，但是LPVG对信号中的噪声具有较强的鲁棒性：分别对周期、随机、分形和混沌四种时间序列进行LPVG建网，发现随着噪声强度增大，LPVG网络聚类系数的波动率均为最低，分别为6.73%、0.05%、0.99%和3.20%。接下来对脑电信号的PSD和LPVG建网分析结果表明，癫痫发作中，PSD值在delta频带下显著增强，而在theta频带下显著降低；LPVG网络拓扑结构有所改变，网络中各模块的独立性有所提高，网络的平均路径长度增大，复杂度降低。所提的功率谱密度和有限穿越可视图算法能够有效表征癫痫前、中、后三种状态下的脑电信号能量分布和单通道信号可视化后的网络拓扑结构的异常，为癫痫的病理研究和临床诊断提供帮助。

脑电信号；癫痫；功率谱密度；有限穿越可视图；复杂网络

0 引言

癫痫是一种严重危害人类安全健康的常见慢性脑部疾病，全世界大约0.5%的人患有癫痫，使运动感觉、自主神经、意识和精神状态等反复出现不同程度的障碍。癫痫发作时表现为大脑神经元兴性增高以及过度同步化放电，并导致短暂性中枢神经系统功能失常[1-2]，患者承受了巨大的痛苦和危险，极大影响了患者及其家庭的生活质量。

脑电图(ElectroEncephaloGram, EEG)是在头皮上通过电极记录的脑细胞群自发性、节律性的电活动轨迹[3]。当大脑出现病理性或功能性改变时，EEG就会发生相应变化[4-5]。此外，脑电图具有时间分辨率高、价格低廉、获取容易且可进行实时监测等优点，日益成为癫痫临床诊断的重要辅助工具，在临床医学和脑科学的研究中都起着不可替代的重要作用[5-7]。癫痫诊断目前大都由医生通过视觉检测患者的脑电图，根据经验诊断完成的。人工视觉检测存在费时、效率低、且缺乏标准的制约等不利因素，因此，癫痫脑电的自动识别与诊断研究具有重大的临床应用价值。

针对这一问题，众多学者致力于癫痫EEG的自动检测技术领域的研究，并提出很多自动检测方法。其中最常见的分析方法主要有时域分析、频域分析、复杂度分析等[8-16]。这些自动方法诊断主要是对脑电信号进行分析，提取癫痫疾病的特征向量，以实现对健康人群与癫痫患者的区分以及癫痫不同时期的区分。大部分的参考文献基于对不同的EEG通道进行谱分析[8-10]。Mporas等[11]通过使用6阶自回归(AutoRegression, AR)模型估计癫痫EEG的功率谱密度并以此为特征进行分类分析，准确率高达近90%。此外，样本熵、多尺度熵、模糊熵、相空间分析等非线性混沌算法也被用来提取脑电特征，用于癫痫的自动诊断研究[12-16]。

近年来，基于复杂网络的非线性时间序列的动力学分析受到了广泛关注[17-20]。如Zhang等[20]在相空间内将准周期时间序列的每一周期作为网络的一个节点，每两个准周期间的距离与所选取的阈值共同决定节点之间是否存在连边，以此将心电信号转化为复杂网络用于心电信号的分析。Gao等[21]将一维时间序列重构到高维的相空间中，由此构成对应原时间序列的复杂网络，并将此相空间重构方法应用于识别与分析多相流的流形。Wang等[22]通过相干性分析将多通道Alzheimer症脑电映射为复杂脑网络，通过网络特征探究Alzheimer脑功能的异常。

2008年Lacasa等[23]提出了一种全新的一维时间序列映射为复杂网络的方法：可视图(Visibility Graph, VG)算法。其思想是将离散时间序列中的数据点作为网络节点，数据点之间满足可视化准则的连线定义为网络连接。可视图算法已成功应用于大脑神经障碍分析、心率分析、飞机湍射流分析、海洋潮汐记录分析、金融经济分析[24-29]。随后，Luque等[30]提出了水平可视图(Horizontal Visibility Graph, HVG)算法。可视图与水平可视图建网方法具有算法简单易实现、计算效率高等优点。但是这两种算法对不同类别的时间序列的识别能力尚存在问题，且对噪声的鲁棒性差。基于此，周婷婷等[31]在此基础上提出了有限穿越可视图(Limited Penetrable Visibility Graph， LPVG)算法，并将其应用于油气水三相流电导波动序列的识别中。Pei等[32]采用LPVG算法成功地区分开了针刺前、中、后的脑电信号。本文采用功率谱密度分析和有限穿越可视图(LPVG)算法对癫痫发作前、中、后阶段的脑电信号进行分析，旨在获取单通道的癫痫脑电序列的谱特征以及EEG序列映射成复杂网络的网络特征，用于癫痫脑电信号的自动识别与诊断，为癫痫的病理研究和临床诊断提供参考。

1 癫痫脑电的采集与预处理

研究所需癫痫病例由河北省唐山市工人医院神经内科提供。目前，临床实验获取癫痫病例已达到70余人。本研究在已获取的病例群中筛选特性相同或相近的5例中度异常病例进行算法研究。5例病例均为EP大发作，具体症状表现为右侧顶中后颞持续大量中高幅尖波尖慢。所有研究病例均为自愿参加，且已签署知情协议。

临床采集脑电实验中，电极帽电极位置按照国际导联10-20系统安放，其中，耳垂作为电极的参考地。实验设备的采样频率为256 Hz，硬件滤波器的为0.5～100 Hz。

实验过程中，对实验病例连续采集记录脑电信号10 min。从每位实验病例的每通道EEG信号中截取发作前(R1)、中(R2)、后(R3)这三段长度为8 s的数据(数据长度为256×8=2 048个采样点)进行分析。采用0～30 Hz的带通滤波器分别对每段数据进行预处理，并采用小波变换提取EEG信号4个子频带：delta(0～4 Hz)、theta(4～8 Hz)、alpha(8～15 Hz)以及beta(15～30 Hz)。图1为theta频带下发作前、中、后三种状态下的脑电信号示意图，可以发现相比发作前、后，癫痫发作中的脑电信号出现异常。

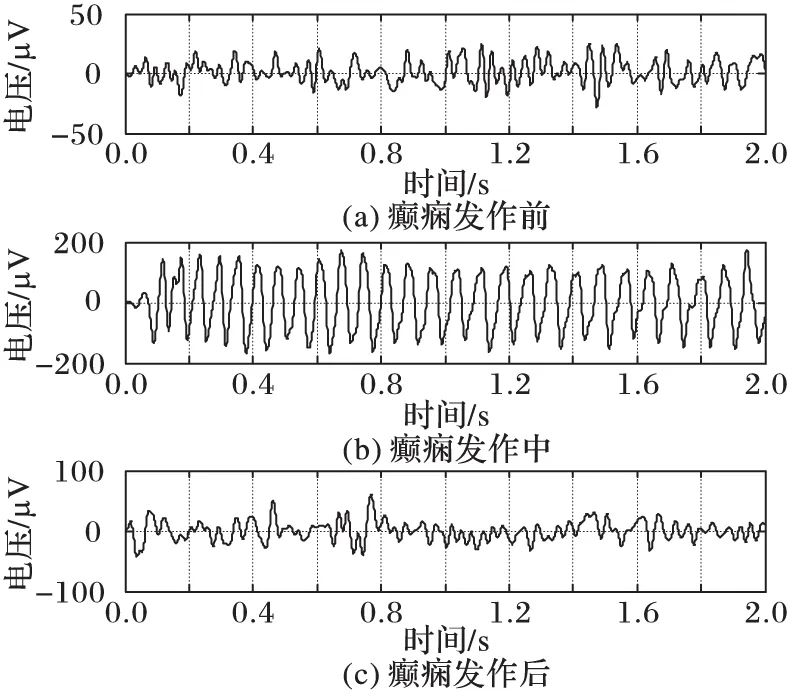
图1 theta频带下三种状态的脑电信号

2 分析方法

本文将采用功率谱密度分析和有限穿越可视图算法分别从能量和网络特征角度对癫痫发作前、中、后三个状态下的单通道脑电信号进行分析，具体过程如图2所示。

2.1 功率谱密度算法

本文采用线性自回归(AR)模型估计法来估计EEG信号的功率谱密度。

AR模型如式(1)所示：

(1)

其中：x(n)为待分析时间序列，u(n)为外加白噪声序列，p是AR模型的阶数，本文中取p=10，ak为模型参数，由Burg算法估计得到，其基本原理是使前向预测与后向预测的均方误差之和最小。

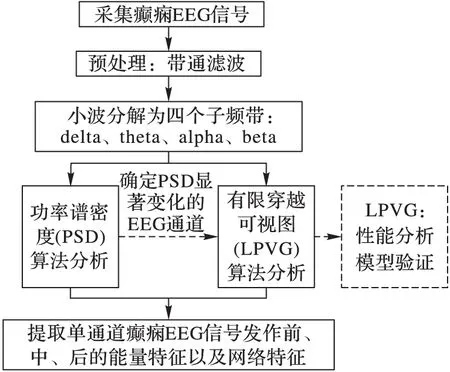
图2 癫痫脑电分析流程

因此，估计出AR模型参数后，可以得到序列x(n)的功率谱密度，如式(2)所示：

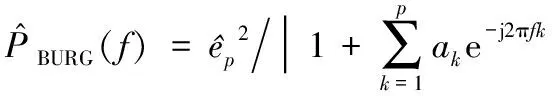
(2)

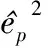
2.2 有限穿越可视图算法

可视图(VG)算法就是通过可视图准则将一维时间序列映射为复杂网络。其思想是将离散时间序列中的数据点作为网络节点，数据点之间满足可视化准则的连线定义为网络连接[23]。

可视化准则如下：长度为N的时间序列{Xi|1,2,…,N}，其中任意两点Xa与Xc之间存在连接等价于这两点间任意一点Xb，满足式(3)：

Xb≤Xc+(Xa-Xc)·(c-b)/(c-a)

(3)

图3(a)中用黑色垂直的直方条表示时间序列的数据点，同时作为网络的节点，直方条的高度表示对应的幅值，根据上述可视化准则将满足条件的点连接起来，用实线表示，构成可视图网络。VG网络具有如下几点性质：每一个点至少和其前后两个邻点相连接；网络连接具有无向性；横轴和纵轴坐标尺度变化或者经过仿射变换后，可视性保持不变。此外，VG算法能够继承原始时间序列的非线性动力学特征，即应用VG算法可将周期时间序列转化成规则网络，随机时间序列转化成随机网络，分形时间序列转化成标度网络。

水平可视图(HVG)算法如图3(b)所示。网络的节点定义与网络的连边方式与VG相同，不同的是，网络节点间的连边必须是水平直线，且不能穿越其他的直方条。因此，对于同一列时间序列，水平可视图是可视图的一个子图，且节点的平均度值较小[30]。

有限穿越可视图(LPVG)算法如图3(c)所示。定义有限穿越视距为N，当且仅当两个节点所对应的直方条之间的连线穿越其他直方条次数满足n≤N时，两节点之间存在连边[31]。图3(c)中实线表示基于VG算法的连边，灰色虚线表示新增有限穿越连边。本文仿真中，有限穿越视距设为N=5。LPVG算法同样具有连接无向性与仿射变换或者坐标轴尺度变换后可视性不变的特点，且LPVG网络具有更强的连接性，长程连接能够反映序列波动趋势。因此，LPVG算法对噪声和干扰具有较强鲁棒性，在含噪情况下仍能较好地继承信号的动力学特性。

图3 三种可视图算法原理示意图

2.3 网络参数

复杂网络的拓扑结构可由以下网络参数[35-37]来表征。

1)节点度和度分布。

节点度衡量单个节点作为功能网络中多个连接交叉点的重要程度。网络中单个节点的度值等于该节点的连接总数。网络的平均度定义为所有节点度的平均值：

(4)

其中：N是网络的节点个数，Ki是节点i的度值，节点度K的分布情况可以用分布函数P(K)表示。

2)平均路径长度。

平均路径长度是网络中所有点对的距离的平均值，度量了网络的整体连通性与不同节点间的集合程度。平均路径长度定义为某一节点到任一其他节点的平均距离：

(5)

其中：dij为节点i和j间的最短距离，N为网络中节点总个数。另一个重要的网络特征参数：聚类系数衡量一个节点最近邻节点之间的连接情况，与平均路径长度呈现相反趋势。

3)图指数复杂度。

图指数复杂度(Graph Index Complexity, GIC)用于衡量功能网络的复杂度。定义式如下：

Cλmax=4m(1-m)

(6)

m=[λmax-2 cos(π/(N+1))]/[n-1-2 cos(π/(N+1))]

(7)

其中λmax为功能网络邻接矩阵的最大特征值。在无向二值网络中，总有2 cos(π/(n+1))≤λmax≤n-1成立，因此，图指数复杂度在[0,1]区间变化。Cλmax越大表明网络结构越复杂。

3 模型验证

在本章中，用正弦周期序列、随机序列、H=0.5(H为Hurst指数)的布朗分形序列以及Lorenz混沌序列来研究有限穿越可视图(LPVG)、可视图(VG)以及水平可视图(HVG)这三种时间序列建网的可视化算法的性能。此外，对四种序列分别添加10 dB、20 dB、30 dB的高斯白噪声信号。简明起见，四种典型时间序列以及添加10 dB高斯白噪声的时间序列如图4所示，而其他噪声强度的序列在图4中不予表示。

分别采用VG、HVG以及LPVG 3种可视图算法对四种典型序列进行建网，可以发现3种可视图算法都具有较好的还原序列的动力学特性。提取3种可视图网络的聚类系数以及平均路径长度，如表1～2所示。可以发现，随着噪声强度的增大，与VG和HVG相比，LPVG算法提取的聚类系数和平均路径长度，其波动率均为最小，可见LPVG对含噪信号具有较好的适应性，具备更佳的抗干扰能力。

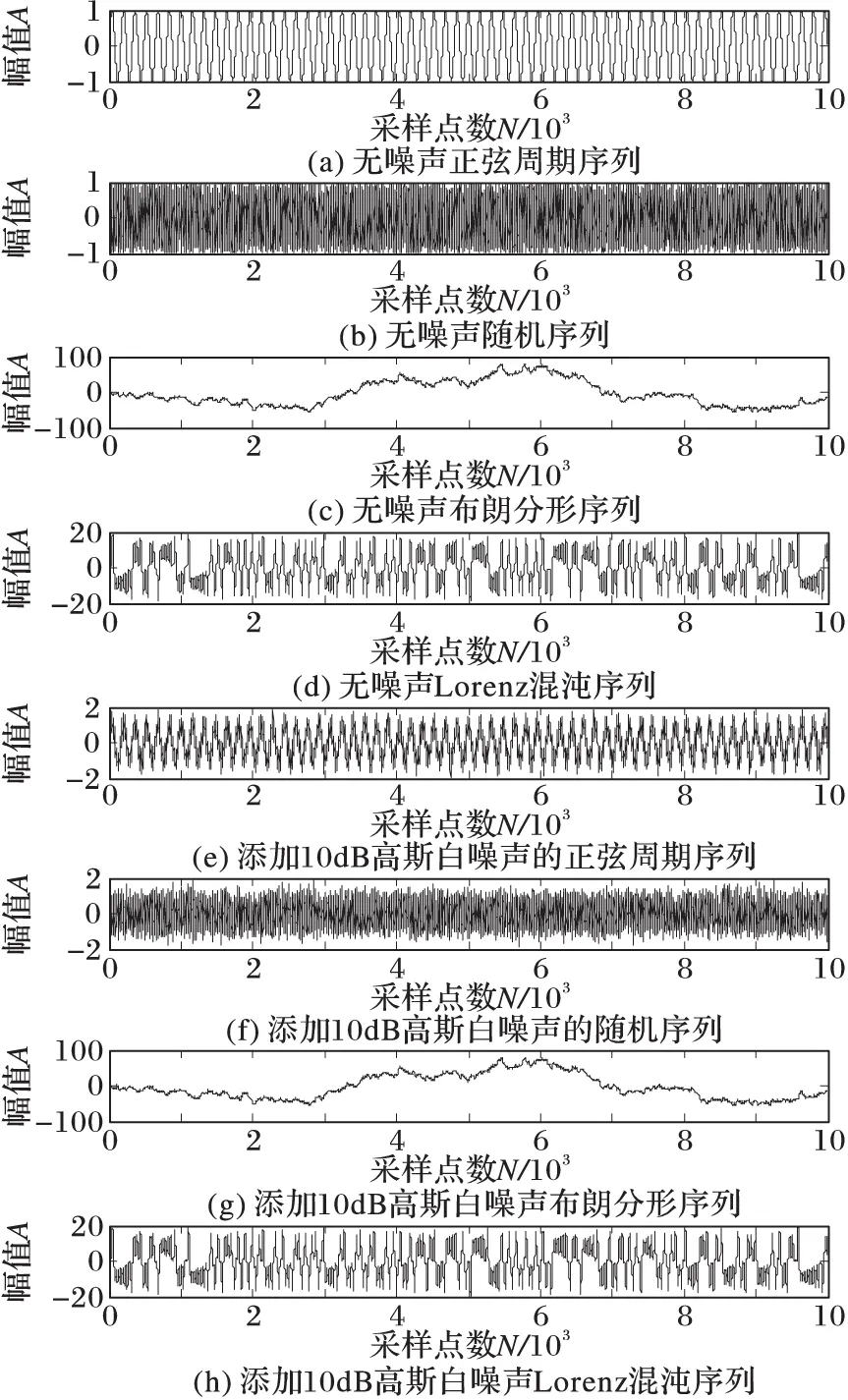
图4 4种典型仿真时间序列示意图

表1 3种可视图算法建网的网络聚类系数对比

Tab.1 Comparison of clustering coefficients of network constructed by three VG algorithms

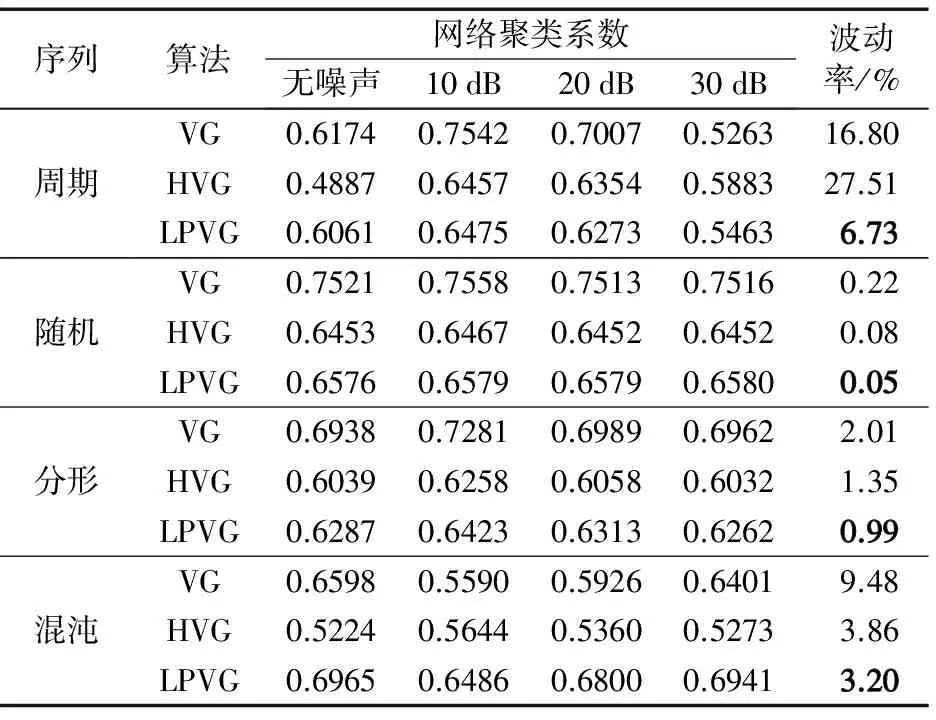
序列算法网络聚类系数无噪声10dB20dB30dB波动率/%周期随机分形混沌VG0．61740．75420．70070．526316．80HVG0．48870．64570．63540．588327．51LPVG0．60610．64750．62730．54636．73VG0．75210．75580．75130．75160．22HVG0．64530．64670．64520．64520．08LPVG0．65760．65790．65790．65800．05VG0．69380．72810．69890．69622．01HVG0．60390．62580．60580．60321．35LPVG0．62870．64230．63130．62620．99VG0．65980．55900．59260．64019．48HVG0．52240．56440．53600．52733．86LPVG0．69650．64860．68000．69413．20

本文对3种可视图算法进行了时间复杂度和空间复杂度分析，计算结果如表3所示。时间复杂度是度量算法执行的时间长短；而空间复杂度是度量算法所需存储空间的大小。

由表3可知，HVG、VG以及LPVG这3种可视图算法的时间复杂度依次增大，表明算法的复杂程度逐渐增大，但计算所需的存储空间均为O(1)量级。此外，3种可视图算法的计算时间如图5(a)所示。仿真时间序列长度设置为2 500个点。图5(b)为采用VG与HVG算法对仿真序列的第2 000～2 500点建网时所耗时间的放大。

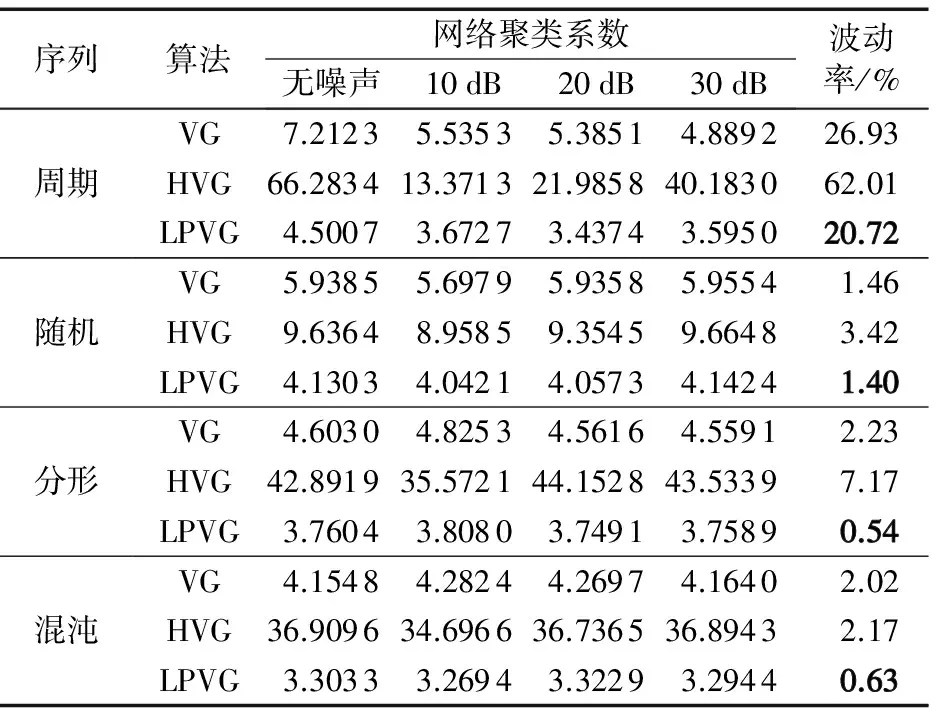
表2 3种可视图算法建网的网络平均路径长度对比

表3 3种可视图算法建网的时间复杂度

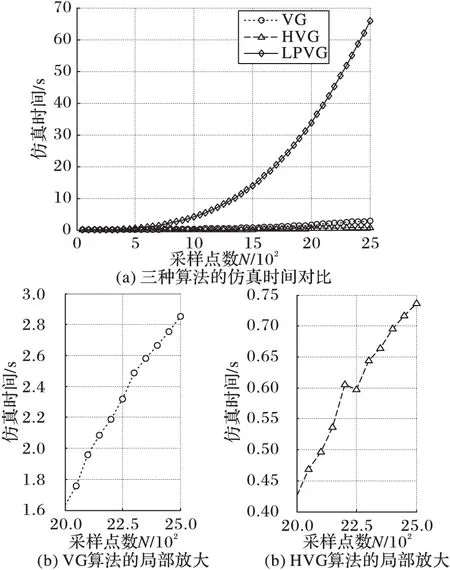
图5 3种可视图算法的计算时间比较

由图5可知，与VG和HVG相比，LPVG算法时间复杂度远大于其他两种可视图算法，且仿真消耗时间也远远大于两种可视图算法。

虽然有限穿越可视图(LPVG)算法的时间复杂度较高，计算时间较长，且在信号识别能力上存在一定的局限性，但是抗噪能力强。在一定程度上，有限穿越可视图以牺牲相邻节点的相关性，来抵抗噪声点的干扰，达到防止重要节点被噪声隔断的目的，能够更好地反映时间序列的动力学特性和波动趋势。如果有限穿越视距N取值小，局部相关性并未全部抹杀。有限穿越可视图在牺牲微观相关性的情况下更能保留信号的宏观信息。

4 实验结果分析

本章将第2章提出的算法应用到癫痫脑电信号发作前、中、后状态的识别上。由于癫痫脑电信号在临床采集过程中含有大量噪声，因此，本章采用功率谱密度(Power Spectrum Density, PSD)以及抗噪能力强的有限穿越可视图(LPVG)算法对脑电信号(EEG)进行分析。

首先将每通道EEG提取为发作前(R1)、发作中(R2)、发作后(R3)三段数据。随后，采用小波分解将三段EEG分解为delta、alpha、theta、beta四个频带，并在每个频带下采用AR Burg参数模型法估计分别19通道脑电信号的功率谱密度。最后，对5名患者的PSD计算结果求平均值，计算结果如图6所示。

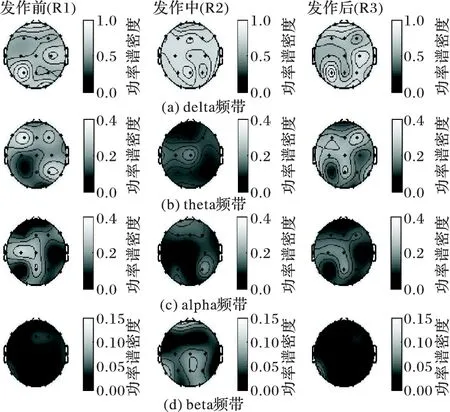
图6 癫痫发作前、中、后的平均功率谱密度地形图

从图6中可知，在delta频带下(图6(a))，大脑普遍EEG能量较高，并且在癫痫发作前与发作后，脑区的能量分布有一定的层次性，而在发作期间，整个脑区能量异常增强，各脑区的能量值显著升高；而在theta频带下(图6(b))，发作期间整个脑区的能量异常减少，脑区之间能量分布的区域性差异显著降低，反映出大脑脑区活动趋于一致性；在alpha频带下(图6(c))，发作前、中、后三个阶段，脑区能量的变化不明显；在beta频带下(图6(d))，脑区能量的分布值很低，且不存在明显变化。

为了进一步分析各个脑区能量变化的规律，本文将大脑分为前额区(F)、左颞区(LT)、中心区(CP)、枕区(O)、右颞区(RT)五个脑区。接下来在各个脑区上，对癫痫发作前、中、后(R1，R2，R3)三个阶段的EEG的功率谱密度(PSD)值进行单因素方差分析，结果如图7所示。当p<0.01(图中用“*”注明)，表明状态之间存在显著性差异。图7中，在delta频带下(图7(a))，脑区能量的变化与地形图分析的结果一致，发作中各个脑区的能量值均高于发作前。与发作后相比，只有前额区、右颞区的能量值相近，并且发作期间各个脑区之间能量的变化没有发作前、中显著；发作中与发作前、后的能量只在右颞区没有显著性区别。delta频带下，在发作中各脑区能量的异常增强，而theta频带下(图7(b))，除中心区以外，各脑区能量均低于发作前和发作后。从能量分布的区域性角度看，发作前、后不同脑区的能量存在较明显的区别，而发作中各脑区能量值趋于一致；除中心区以外，其余各脑区发作中与前、后能量存在显著差异。而alpha和beta频带下(图7(c)、(d))的能量值较低，各脑区能量的变化无明显规律。

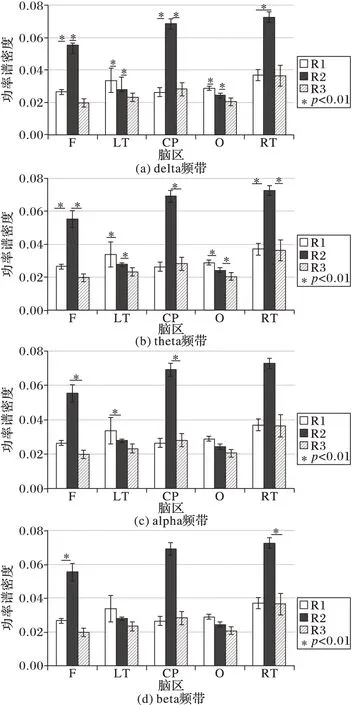
图7 4个频带下癫痫发作前、中、后各脑区功率谱密度的显著性分析

接下来，对发作前、中、后能量存在显著变化的theta频带下的第六通道EEG信号C4采用有限穿越可视图(LPVG)进行分析。序列长度选取为2 000个数据点。图8为构造的复杂网络的邻接矩阵，构造的复杂网络能较好地还原脑电序列的时域特性，并且对噪声具有极强的适应能力。由图8所示可知，采用LPVG算法提取的发作前、中、后三种状态下的EEG序列的邻接矩阵中看出：theta频带下，矩阵中社团连接主要集中在对角线上，其他区域的社团连接面积都较小。发作前、后(图8(a)、(c))，对角线上社团连接大小随机分布，而发作中(图8(b))，社团连接面积有所增大，但分布呈现一定的规律性，表明发作中网络的复杂性有所降低。综上，发作发作前、后，网络模块分布无规则，各模块大小有明显区分；而发作中，网络中各模块大小趋于一致，并且小规模的网络各模块明显减少，各模块的独立性有所提高，网络的复杂度降低，相对趋向于规则网络。

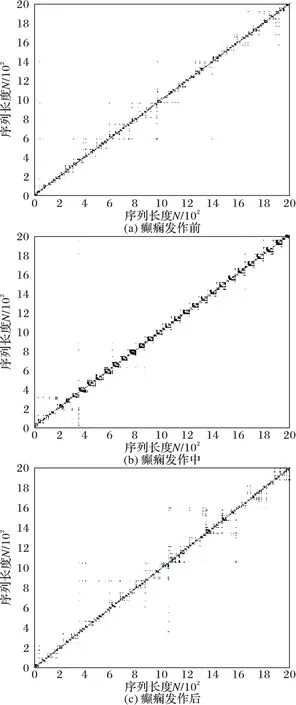
图8 有限穿越可视图网络矩阵

图9为theta频带下网络的节点度和度分布。可以发现，发作中(图9(b))，网络的度值明显高于发作前、后(图9(a)、(c))，且度分布的峰值增大且峰值右移，概率最大的度值接近40，而发作前、后概率最大的度值在20左右。而发作后与发作前相比，节点度分布要分散一些，但总体变化不明显。

图10为采用LPVG对癫痫发作前、中、后的EEG序列在delta、theta、alpha和beta四个频带下分别构建，并提取网络特征参数：平均路径长度和图指数复杂度(GIC)。由图10(a)可知，在theta和alpha频带下，前、中、后三种状态下区分不明显；在delta频带下，发作中网络的平均最短路径高于发作前、后，表明网络信息传递减慢；在beta频带下，发作中网络的平均路径长度变小，考虑到高频带包含的信息量较少，因此，对分析结果没有明显影响。图10(b)可知，网络的复杂度随着频带增高而降低，在delta和theta频带下，发作中网络的复杂度要低于前、后，其中在delta频带的衰减最为显著，表明癫痫发作期间，虽然delta频带脑电能量急剧增强，但脑网络的复杂度降低，与EEG信号呈周期性变化相对应；而在alpha和beta频带下，复杂度改变不明显，对应高频带下网络信息量较低。

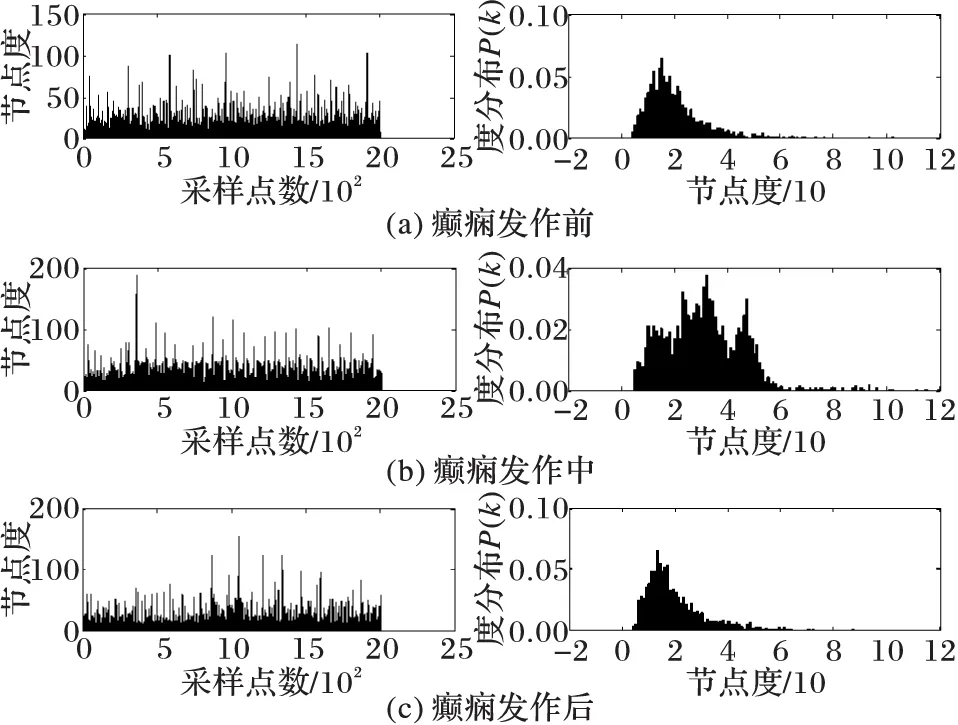
图9 theta频带下有限穿越可视图网络的节点度以及度值概率分布

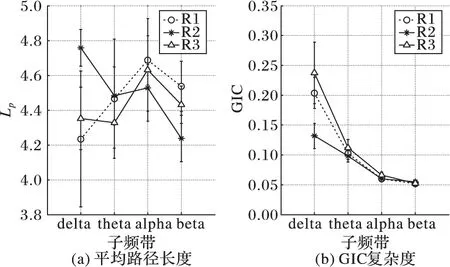
图10 4个频带下癫痫发作前、中、后的网络特征

5 结语

为探究癫痫发作对脑电信号的影响，本文采用功率谱密度和有限穿越可视图算法算法分析癫痫发作前、中、后三种状态下的单通道脑电信号能量分布以及脑电信号的网络特征。研究发现，癫痫发作时，脑电信号能量分布发生明显改变，能量向低频带转移，表现为delta频带能量显著增加，而theta频带能量明显降低。对脑区能量分布的进一步研究发现，在delta频带下，发作前与发作后各脑区能量均有显著性差异；在theta频带下，除中心区外，各脑区均有显著性差异，表明癫痫发作对大部分脑区在低频带的脑电信号影响较大。对第六通道C4在theta频带下的发作前、中、后三种状态下对应的EEG信号进行有限穿越可视图(LPVG)分析，发现三种状态下，LPVG构建的复杂网络具有不同形态的拓扑结构，发作中时更接近于规则网络。与发作前、后相比，在高频带(alpha和beta)下，发作中网络的平均最短路径减小，而在低频带(delta和theta)显著增大，且网络的复杂度明显降低。本文研究结果表明，功率谱密度和有限穿越可视图算法能够有效表征癫痫前、中、后三种状态下脑电信号能量分布和单通道信号可视化后的网络拓扑结构的异常，为癫痫的病理研究和临床诊断提供帮助。

References)

[1] HANSEN B H, ALFSTAD K A, Van ROY B, et al.Sleep problems in children and adolescents with epilepsy: Associations with psychiatric comorbidity [J].Epilepsy & Behavior, 2016, 62: 14-19.

[2] PUKA K, RUBINGER L, CHAN C, et al.Predictors of intellectual functioning after epilepsy surgery in childhood: the role of socioeconomic status [J].Epilepsy & Behavior, 2016, 62: 35-39.

[3] NAVARRO-SUNE X, HUDSON A L, DE VICO FALLANI F, et al.Riemannian geometry applied to detection of respiratory states from EEG signals: the basis for a brain-ventilator interface [EB/OL].[2016-04-20].https://arxiv.org/pdf/1601.03022.

[4] SHEN C, LIU S, ZHOU W, et al.A physiology-based seizure detection system for multichannel EEG [J].PLoS One, 2013, 8(6): e65862.

[5] CZIGLER B, CSIKóS D, HIDASI Z, et al.Quantitative EEG in early Alzheimer’s disease patients-power spectrum and complexity features [J].International Journal of Psychophysiology, 2008, 68(1): 75-80.

[6] KLOVATCH-PODLIPSKY I, GAZIT T, FAHOUM F, et al.Dual array EEG-fMRI: an approach for motion artifact suppression in EEG recorded simultaneously with fMRI [EB/OL].[2016-03-20].http://www.sciencedirect.com/science/article/pii/S1053811916303214.

[7] SCHLEIGER E, WONG A, READ S, et al.Improved cerebral pathophysiology immediately following thrombectomy in acute ischaemic stroke: Monitoring via quantitative EEG [J].Clinical Neurophysiology : Official Journal of the International Federation of Clinical Neurophysiology, 2016, 127(8): 2832-2833.

[8] 李昌强,黄力宇,鞠烽炽,等.癫痫脑电的双谱特性研究[J].北京生物医学工程,2004,23(1):9-13.(LI C Q, HUANG L Y, JU F Z, et al.Study of epileptic electroencephalogram using bispectrum analysis [J].Beijing Biomedical Engineering, 2004,23(1): 9-13.)

[9] 刘建平,张一闻.一种高分辨率时频分析方法及在脑电信号处理中的应用[J].武警工程学院学报,2002,18(6):19-22.(LIU J P, ZHANG Y W.A high resolution time frequency analysis method and its application in EEG signal processing [J].Journal of Engineering University of the Chinese People’s Armed Police Force, 2002, 18(6): 19-22.)

[10] ADELI H, ZHOU Z, DADMEHR N.Analysis of EEG records in an epileptic patient using wavelet transform [J].Journal of Neuroscience Methods, 2003, 123(1): 69-87.

[11] MPORAS I, TSIRKA V, ZACHARAKI E I, et al.Seizure detection using EEG and ECG signals for computer-based monitoring, analysis and management of epileptic patients [J].Expert Systems with Applications, 2015, 42(6): 3227-3233.

[12] 杜守洪,陈子怡,田翔华,等.近似熵与SVM在自动分类癫痫脑电信号中的应用[J].生物医学工程研究,2013,32(2):74-79.(DU S H, CHEN Z Y, TIAN X H, et al.Epilepsy EEG Approximate Entropy (ApEn) Support Vector Machine (SVM) real-time detection classification [J].Journal of Biomedical Engineering Research, 2013, 32(2):74-79.)

[13] 张涛,陈万忠,李明阳.基于AdaBoost算法的癫痫脑电信号识别[J].物理学报,2015,64(12):128701.(ZHANG T, CHEN W Z, LI M Y.Recognition of epilepsy electroencephalography based on AdaBoost algorithm [J].Acta Physica Sinica, 2015, 64(12): 128701.)

[14] XIANG J, LI C, LI H, et al.The detection of epileptic seizure signals based on fuzzy entropy [J].Journal of Neuroscience Methods, 2015, 243:18-25.

[15] TAKAHASHI T, CHO R Y, MIZUNO T, et al.Antipsychotics reverse abnormal EEG complexity in drug-naive schizophrenia: a multiscale entropy analysis [J].Neuroimage, 2010, 51: 173-182.

[16] SONG Y, CROWCROFT J, ZHANG J.Automatic epileptic seizure detection in EEGs based on optimized 21 sample entropy and extreme learning machine [J].Journal of Neuroscience Methods, 2012, 210: 132-146.

[17] FELDHOFF J H, DONNER R V, DONGES J F, et al.Geometric detection of coupling directions by means of inter-system recurrence networks [J].Physics Letters A, 2013, 376(46): 3504-3513.

[18] DEZA J I, BARREIRO M, MASOLLER C.Inferring interdependencies in climate networks constructed at inter-annual, intra-season and longer time scales [J].European Physical Journal Special Topics, 2013, 222(2):511-523.

[19] FELDHOFF J H, DONNER R V, DONGES J F, et al.Geometric detection of coupling directions by means of inter-system recurrence networks [J].Physics Letters A, 2012, 376(46):3504-3513.

[20] ZHANG J, SMALL M.Complex network from pseudoperiodic time series: topology versus dynamics [J].Physical Review Letters, 2006, 96(23): 238701-238701.

[21] GAO Z, JIN N.Flow-pattern identification and nonlinear dynamics of gas-liquid two-phase flow in complex networks [J].Physical Review E: Statistical Nonlinear & Soft Matter Physics, 2009, 79(6): 1019-1027.

[22] WANG R, WANG J, YU H, et al.Decreased coherence and functional connectivity of electroencephalograph in Alzheimer’s disease [J].Chaos, 2014, 24(3): 033136-033136.

[23] LACASA L, LUQUE B, BALLESTEROS F.From time series to complex networks: the visibility graph [J].Proceedings of the National Academy of Sciences of the United States of America, 2008, 105(13): 4972-4975.

[24] MEHRAN A, HOJJAT A.Visibility graph similarity: a new measure of generalized synchronization in coupled dynamic systems [J].Physica D: Nonlinear Phenomena, 2012, 241(4): 326-332.

[25] MEHRAN A, HOJJAT A, AMIR A.Improved visibility graph fractality with application for the diagnosis of autism spectrum disorder [J].Physica A: Statistical Mechanics & Its Applications, 2012, 391(20): 4720-4726.

[26] JIANG S, BIAN C, NING X, et al.Visibility graph analysis on heartbeat dynamics of meditation training [J].Applied Physics Letters, 2013, 102(25): 253702-1-253702-3.

[27] TELESCA L, LOVALLO M, PIERINI J O.Visibility graph ap-proach to the analysis of ocean tidal records [J].Chaos Solitons & Fractals, 2012, 45(9/10): 1086-1091.

[28] CHARAKOPOULOS A K, KARAKASIDIS T E, PAPANICOLAOU P N, et al.The application of complex network time series analysis in turbulent heated jets [J].Chaos, 2014, 24(2): 024408-024408.

[29] WANG N, LI D, WANG Q.Visibility graph analysis on quarterly macroeconomic series of China based on complex network theory [J].Physica A: Statistical Mechanics & Its Applications, 2012, 391(24): 6543-6555.

[30] LUQUE B, LACASA L, BALLESTEROS F, et al.Horizontal visibility graphs: exact results for random time series [J].Physical Review E: Statistical Nonlinear & Soft Matter Physics, 2009, 80(2): 593-598.

[31] 周婷婷,金宁德,高忠科,等.基于有限穿越可视图的时间序列网络模型[J].物理学报,2012,61(3):030506.(ZHOU T T, JIN N D, GAO Z K, et al.Limited penetrable visibility graph for establishing complex network from time series [J].Acta Physica Sinica, 2012, 61(3): 030506.)

[32] PEI X, WANG J, DENG B, et al.WLPVG approach to the analysis of EEG-based functional brain network under manual acupuncture [J].Cognitive Neurodynamics, 2014, 8(5): 417-428.

[33] AKIN M, KIYMIK M K.Application of periodogram and AR spectral analysis to EEG signals [J].Journal of Medical Systems, 2000, 24(4): 247-256.

[34] LI L, XIAO L, CHEN L.Differences of EEG between eyes-open and eyes-closed states based on autoregressive method [J].Journal of Electronic Science and Technology of China, 2009, 7(2): 175-179.

[35] STAM C J, REIJNEVELD J C.Graph theoretical analysis of complex networks in the brain [J].Nonlinear Biomedical Physics, 2007, 1: 3.

[36] KIM J, WILHELM T.What is a complex graph? [J].Physica A: Statistical Mechanics and its Applications, 2008, 387(11): 2637-2652.

[37] BOCCALETTI S, LATORA V, MORENO Y, et al.Complex networks: structure and dynamics [J].Complex Systems & Complexity Science, 2007, 424(4/5): 175-308.

This work is partially supported by the National Natural Science Foundation of China (61302002, 61601331), the Natural Science Foundation of Tianjin City (14JCYBJC15400, 14JCQNJC01200), Tangshan Technology Research and Development Program (14130223B), Advance Research Program of Tianjin University of Technology and Education (KYQD1611).

WANG Ruofan, born in 1986, Ph.D., lecturer.Her research interests include data analysis and algorithm mining, analysis of complex nonlinear system.

LIU Jing, born in 1973, Ph.D., chief physician.Her research interests include neurology.

WANG Jiang, born in 1964, Ph.D., professor.His research interests include neural computing.

YU Haitao, born in 1985, Ph.D., lecturer.His research interests include nervous system modeling and kinetic analysis.

CAO Yibin, born in 1963, M.S., chief physician.His research interests include neurology.

Analysis algorithm of electroencephalogram signals for epilepsy diagnosis based on power spectral density and limited penetrable visibility graph

WANG Ruofan1, LIU Jing2, WANG Jiang3, YU Haitao3, CAO Yibin2*

(1.CollegeofInformationTechnologyEngineering,TianjinUniversityofTechnologyandEducation,Tianjin300222,China;2.DepartmentofNeurology,TangshanGongrenHospital,TangshanHebei064300,China;3.CollegeofElectrical&AutomationEngineering,TianjinUniversity,Tianjin300072,China)

Focused on poor robustness to noise of the Visibility Graph (VG) algorithm, an improved Limited Penetrable Visibility Graph (LPVG) algorithm was proposed.LPVG algorithm could map time series into networks by connecting the points of time series which satisfy the certain conditions based on the visibility criterion and the limited penetrable distance.Firstly, the performance of LPVG algorithm was analyzed.Secondly, LPVG algorithm was combined with Power Spectrum Density (PSD) to apply to the automatic identification of epileptic ElectroEncephaloGram (EEG) before, during and after the seizure.Finally, the characteristic parameters of the LPVG network in the three states were extracted to study the influence of epilepsy seizures on the network topology.The simulation results show that compared with VG and Horizontal Visibility Graph (HVG), although LPVG had a high time complexity, it had strong robustness to noise in the signal: when mapping the typical periodic, random, fractal and chaos time series into networks by LPVG, it was found that as the noise intensity increased, the fluctuation rates of clustering coefficient by LPVG network were always the lowest, respectively 6.73%, 0.05%, 0.99% and 3.20%.By the PSD and LPVG analysis, it was found that epilepsy seizure had great influence on the brain energy.PSD was obviously enhanced in the delta frequency band, and significantly reduced in the theta frequency band; the topological structure of the LPVG network changed during the seizure, characterized by the independent enhanced network module, increased average path length and decreased graph index complexity.The PSD and LPVG applied in this paper could be taken as an effective measure to characterize the abnormality of the energy distribution and topological structure of single EEG signal channel, which would provide help for the pathological study and clinical diagnosis of epilepsy.

ElectroEncephaloGram (EEG); epilepsy; Power Spectral Density (PSD); Limited Penetrable Visibility Graph (LPVG); complex network

2016-08-10;

2016-09-28。 基金项目:国家自然科学基金资助项目(61302002， 61601331)；天津市自然科学基金资助项目(14JCYBJC15400， 14JCQNJC01200)；唐山市科技支撑项目(14130223B)；天津职业技术师范大学预研项目(KYQD1611)。

王若凡(1986—)，女，河北沧州人，讲师，博士，主要研究方向：数据分析与算法挖掘、复杂非线性系统分析； 刘静(1973—)，女，河北唐山人，主任医师，博士，主要研究方向：神经病学； 王江(1964—)，男，河北唐山人，教授，博士，主要研究方向：神经计算； 于海涛(1985—)，男，河北唐山人，讲师，博士，主要研究方向：神经系统建模与动力学分析； 曹亦宾(1963—)，男，河北唐山人，主任医师，硕士，主要研究方向：神经病学。

1001-9081(2017)01-0175-08

10.11772/j.issn.1001-9081.2017.01.0175

TP391.4

A