物理模型教学与思维能力培养探究
2017-04-15李乔中
李乔中


【摘要】本文从物理模型的种类、特性、建立和应用上阐述了物理模型教学方法,旨在加强学生对物理概念、规律的理解,培养分析解决物理问题的能力。
【关键词】物理模型教学;理想化;思维能力
所谓物理模型就是对所研究的对象和过程摒弃无关因素,略去次要因素后,所建立起来的能反映事物本质特征的抽象模型。加强物理模型教学,让学生了解物理模型的意义、特点及建立过程,并运用物理模型解决实际问题,这是培养物理思维能力的一个重要途径。
一、物理模型的种类
物理模型分类有不同的标准。以研究的目的为标准,物理模型可分为描述对象、状态和过程模型。描述对象模型有质点、单摆、理想气体、点电荷、匀强电场、匀强磁场和点光源等;状态和过程模型有匀速运动、弹性碰撞和简谐运动等。以作用效果为标准,可分为作用等效模型(如两个分力之合力),过程等效模型(如平抛运动与水平方向匀速运动和竖直方向自由落体运动的合运动等效)。利用作用等效模型可帮助理解概念,培养逆向思维能力;利用过程等效模型可培养分析解决问题和“跃迁思维”能力。
二、物理模型的特性
物理模型一般应具有以下三个特性:(1)简化性。把问题转化为理想物理模型,会使繁杂问题简单化,隐晦问题明朗化。(2)代表性。通过对事物类化的过程,可使物理模型成为具有同样属性事物的代表。(3)变化性。把本来就具有多重性的事物,转化成不同的物理模型。
三、物理模型的建立
物理模型是通过抽象概括建立的。比如质点是一个具有质量的几何点,由于很多力学问题中物体的大小和形状的影响可以不计,为了突出物体的质量这个主要因素,经过物理抽象建立质点模型。建立物理模型的原则:(1)根据所研究问题的需要和可能,突出研究对象的主要因素,忽略次要因素,将研究对象理想化。例如理想气体模型的建立,就是突出了气体实验定律中参量之间的关系,而忽略了对这些参量关系的约束条件,认为这些参量之间的关系在任何条件下都是适用的,这样就把实际气体抽象为理想气体,好似把物体抽象为质点。(2)在模型的基础上,能够建立该领域的知识体系,如果一个模型不能提供一个知识体系,这个模型就没有生命力,就没有存在的价值。如理想气体模型的建立,与之相应的建立了气体分子的质量模型,从而形成了气体分子运动论这个知识体系。
建立理想化物理模型是一种物理的思维模式,也是物理研究的重要方法。物理学的各部分知识体系几乎都是建立在一些模型的基础上。让学生了解物理模型的意义和建立过程,这是培养物理思维能力的重要途径之一;在日常教學中强化这种建立物理模型的思想,使学生在潜移默化中提高利用模型处理物理问题的能力。
四、物理模型的应用
对物理模型认识的一般过程可以用图1表示。对一个物理模型的掌握,关键在于能否运用模型解决实际问题,而运用模型时,反过来又可以巩固建立的模型和加深对模型的理解。物理模型的运用,其关键在于将具体的物理问题变换为物理模型,再运用物理模型中的规律去解决。
变换物理模型的主要途径为:
1、运用移植法变化物理模型。即把原有的处理物理问题的方法移植到不同性质的物理模型中,以求得简捷的解决方法。
例1:如图2所示,BC为竖直放置的长为L=0.5m的平面镜,一小球从某高处自由落下,其轨道跟镜面相距d=0.25m,A处观察者能在镜中看到小球的像的时间为0.4s,a=b=0.4s,求小球从静止下落到观察者能从镜中看到它的像时所经历的时间。
分析:本题运用移植法变换物理模型,把力学模型移植到光学中去求解,由平面镜成像性质决定0.4s内小球下落的高度,由自由落体运动的性质决定小球下落多长时间才能看到它的像。
2、运用等效法变换物理模型。即通过易于被研究的物理模型代替陌生、复杂的物理问题,使研究过程由难变易。
例2:如图3所示,一长为L的细线,上端固定,下端栓一质量为m的带电小球,将它置于场强大小为E的水平向右的匀强电场中,当处于平衡时,细线与竖直方向成α角(α≤45°),如果使偏角由α增大到β,然后由静止释放,则β应为多大才能使细线到达竖直位置时,小球的速度刚好为0?
分析:本题应用等效力场模型转换求解,本题的原型是重力场中的单摆模型,现在小球不仅受重力作用,同时还受到电场力作用,若将这两个力合成一个了,则容易判断小球的平衡位置在O点,小球从A点释放后,在A、B之间来回振动的情况与原型类似,则小球相当于悬挂在一个特殊场中的摆球,由原型的结论推知小球通过平衡位置O时速度最大,在到达振幅位置A、B时速度为0,由对称性可判定β=2α。
3、运用类比法变换物理模型。即同类物理问题的变换,把不易建立的物理模型转化为已经掌握的物理模型,缩短推理过程。
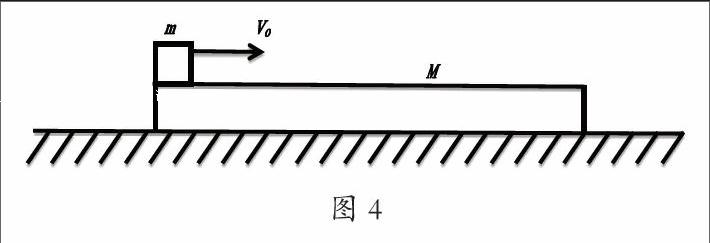
例3:如图4所示,有一质量为M的平板静止于光滑水平面上,平板的左端有一质量为m的物体以初速度v0在平板上向右滑动,摩擦力恒为f,当m与M无相对滑动时,m相对M滑行的距离s为多大?
分析:本题类似于子弹射击木块问题,属于碰撞模型,利用动量守恒条件和功能关系很容易求解。
总之,在物理教学中教师要有目的、有计划地应用物理模型的变换方法来研究和处理比较复杂的物理问题,并及时归纳、总结、提高,这不但能使学生加深对物理概念和规律的理解,提高解题技巧,促进知识的迁移、技能的培养,而且还对开发创造性思维、培养分析和解决问题的能力有明显效果。
