基于负荷曲线的建筑物变压器优化选择

傅军栋,李江辉,张 洋

（1.华东交通大学电气与自动化工程学院，江西 南昌 330013；2.江西省建筑设计研究总院，江西 南昌 330046）

基于负荷曲线的建筑物变压器优化选择

傅军栋1,李江辉1,张 洋2

（1.华东交通大学电气与自动化工程学院，江西 南昌 330013；2.江西省建筑设计研究总院，江西 南昌 330046）

考虑变压器的经济性，建立变压器年运行费用数学模型，以变压器的电能损耗费用、基本电费以及设备投资折旧和维护费用最小为目标函数，基于不同类型建筑物的负荷曲线，采用遗传算法对模型进行求解，得到建筑物所选变压器的台数和容量。通过对具体实例进行分析，验证了上述模型的准确性和求解算法的有效性。

建筑物；负荷曲线；遗传算法；变压器选择

根据《工业与民用配电设计手册》规定，变压器台数的选取应根据用电负荷特点、经济运行条件、节能和降低工程造价等因素综合确定。对于有大量一级或二级用电负荷、用电负荷季节性变化较大或集中用电负荷较大的单位，宜设置2台及以上的变压器。变压器容量应根据计算负荷选择[1]。

建筑供配电设计中负荷计算的方法有需用系数法、利用系数法、单位指标法等几种。在实际的建筑工程设计中，广泛采用需用系数法，根据供配电计算负荷，利用经验公式选择变压器，过程繁琐，效率较低。文献[2]从理论上介绍如何选择变压器的容量并使其做到经济运行，并分析了经济运行的几种方法。文献[3]通过推导变压器的最佳负载率，来说明合理选择变压器的容量能使变压器处于最经济的运行状态。文献[4]通过对配电变压器经济容量常用选择方法及主要影响因素的分析，提出一种更加合理有效的经济容量选择方法。文献[5]探讨了变压器容量选择应考虑的因素和方法，以便能够实现变压器的经济运行。文献[6]主要考虑变压器运行时自身的损耗及运行经济性来选择配电变压器容量。文献[7-8]对变压器的损耗及其经济运行进行了探讨。上述文献从不同的角度阐述了如何经济合理的选择变压器，但均未将负荷曲线纳入考虑之中，没有具体研究负荷曲线对变压器容量选择的影响。为此，本文对不同负荷曲线情况下变压器的选择作了详细介绍，充分考虑负荷的特性和变化规律，建立变压器的年运行费用数学模型，基于不同类型建筑物的负荷曲线，将遗传算法应用到模型的求解中。

1 基于负荷曲线的数学模型

1.1 模型目标函数和约束条件

根据不同类型建筑物的负荷曲线，建立变压器年运行费用数学模型，目标函数是变压器总的年运行费用最小化，包括电能损耗费用、基本电费以及设备投资折旧和维护费用[9-10]。以变压器年运行费用最小方案为最优方案。模型如下：

式中：C为变压器年运行费用，万元；C1为变压器年电能损耗费用，万元；C2为变压器年基本电费，万元；C3为变压器年设备投资折旧和维护费用，万元。

约束条件如下：

1）变压器台数约束。

式中：N为变压器的台数。

2）变压器容量约束。

式中：SN为变压器的额定容量，kVA。

3）功率因数约束。

当年有功负荷曲线确定后，可以从图1中读取N台变压器担负的年最大负荷总有功功率Pm，电力供电部门一般要求用户高压侧的平均功率因数应达到0.9以上[11]。因此有如下约束关系：

式中：cosφ为补偿后的总的功率因数。

4）负荷率约束。

变压器的负荷率β主要影响变压器的经济运行，要使变压器在最佳负荷下经济运行，应满足变压器单位容量的有功功率损耗换算值∑P/SC为最小极值的条件，其中SC＝Pmax/β cosφ，为变压器补偿后的负荷容量，kVA；所以由可得变压器的最佳负荷为

变压器的负荷率β为

则由式（5）、式（6）可得变压器的最佳负荷率为

由于变压器的损耗与负荷率有关，负荷率对变压器的经济运行影响较大，实践表明，变压器的平均工作效率接近于相应变压器的最佳负荷率，负荷率β取值范围宜在70%～80%[12]。因此有如下约束关系：

1.2 负荷曲线

负荷曲线是用来表示一组用电设备的用电功率随时间变化关系的图形，可以直观地反映出用户用电的特点和规律。其中年有功负荷曲线代表用户全年内用电负荷的变化规律，是根据各个不同的有功负荷值在一年中的累计持续时间而重新排列组成的，反映了全年负荷变动与对应的负荷时间（全年按8 760 h计）的关系，如图1所示，横坐标表示有功负荷变动时间，h；纵坐标表示有功负荷大小，kW；Pm表示年最大有功负荷。

对于同类型的用户，其负荷曲线形状大致相同。本文选取南昌市某办公建筑、住宅建筑和商业建筑为供电研究对象，其建筑面积分别为19 800，13 000 m2和21 150 m2；分析其2015—2016年的用电负荷情况，借助一年中具有代表性的夏季和冬季日负荷曲线，绘制其年持续负荷曲线如图2、图3和图4所示，其年最大有功负荷分别为1 100，580 kW和2 350 kW。

图1 年负荷曲线Fig.1 Annual load curve

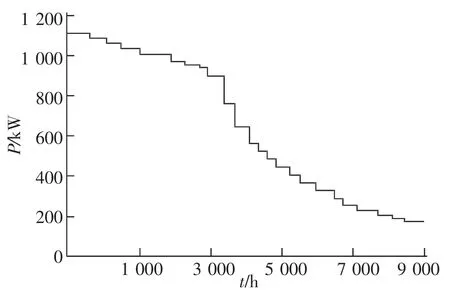
图2 办公建筑负荷曲线Fig.2 Office building load curve

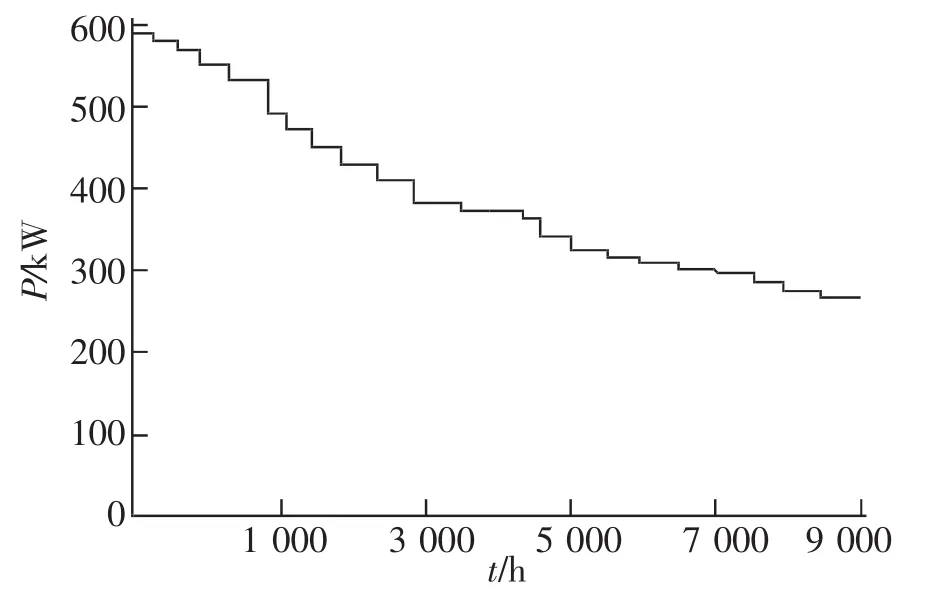
图3 住宅建筑负荷曲线Fig.3 Residential building load curve

图4 商业建筑负荷曲线Fig.4 Commercial building load curve

1.3 电能损耗费用

变压器的总损耗是变压器本身的有功损耗和无功损耗在电力系统中引起有功损耗的增量，或称为变压器的有功损耗换算值。单台变压器的有功损耗换算值为

式中：∑P为变压器有功损耗换算值，kW；△PT为变压器的有功损耗，kW；△QT变压器的无功损耗，kvar。其中变压器的有功损耗包括：

无功损耗包括：

本次88例剖腹产手术患者经过有效护理,平均住院时间为(7.2±2.1)天;其中5例切口脂肪液化患者经及时处理也如期出院,所有患者均痊愈出院。

式中：△P0为变压器的空载损耗，kW；△PKN为变压器的短路损耗，kW；△Q0为变压器空载时的无功损耗增量，kvar；△QN为变压器额定负荷时的无功损耗增量，kvar；Pm为 N台变压器担负的最大负荷总有功功率，kW；SN为变压器的额定容量，kVA；cosφ为功率因数。

用α表示有功负荷系数，其公式为

式中：Pav为建筑物的平均负荷，kW；Pm为建筑物的最大负荷，kW。

建筑场的平均负荷可按式（13）计算

式中：ρ为负荷密度，kW/m2；A为建筑物的面积，m2。

由于负荷系数是表征负荷变化规律的一个参数，相同类型的电力用户具有近似的负荷系数[12]。本文假设相同类型的建筑物具有相同类型的电力用户，其负荷系数的大小相等，根据式（12）和（13）可得

式中：β为建筑物年负最大有功负荷与建筑面积的比值。

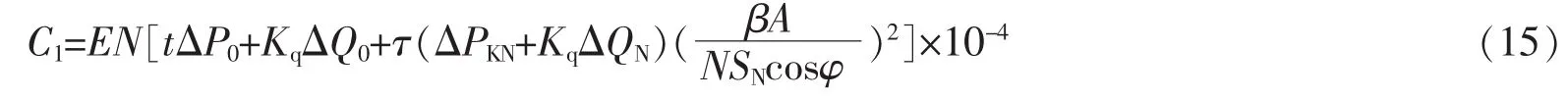
式中：C1为变压器年电能损耗费用，万元；E为电价费，经查资料可知中国居民用电当前的一般价格为：

0.52～0.62元/kWh，本文取0.55元/kWh；N为变压器的台数；t为变压器年运行小时数，取8 760 h；Kq为无功功率经济当量换算系数，本文取0.10 kW/kvar；τ为变压器年最大负荷损耗小时数，根据《工业与民用配电设计手册》选择，城市生活计算值为1 250 h。

1.4 基本电费

基本电费按变压器的安装容量计算，基本电价全国大约在15～30元/(kW·月)，参照本地供电部门执行的电价，本文取20元/(kW·月)。

式中：C2为变压器年基本电费，万元。

1.5 设备折旧和维护费用

本设计中采用SCB10环氧树脂浇注干式变压器，通过查阅资料，假设模型中每台变压器的投资费用为10万元，则变压器的总投资费用为10 N万元，折旧维护系数取10%，则变压器年设备投资折旧维护费用为

式中：C3为变压器年设备投资折旧和维护费用，万元。

2 求解算法

2.1 种群初始化

本文采用遗传算法求解变压器年运行费用的模型[13-14]。采用实数编码的方式，每个染色体为一个方案，每个方案有两个元素，第一个元素代表所选变压器的台数，第二个元素代表所选变压器的容量。结合数学模型，初始种群要满足一定的约束条件。初始种群产生的步骤如下：

1）根据实际情况结合约束条件确定变量的取值范围；

2）在步骤（1）的变量范围内，随机生成初始种群，该种群定义有sizepop个染色体，其中sizepop为种群的规模。初始种群生成。

2.2 遗传操作

算法采用轮盘赌法进行选择操作，并加入最优个体保存策略，以保证算法全局收敛性。交叉操作和变异操作分别采用两点交叉算子和单点变异算子[15]。

2.3 适应度函数

本文是求变压器年运行费用的最小值，把年运行费用函数值的倒数作为个体的适应度值，根据模型目标函数minC＝C1＋C2＋C3可以得到适应度函数Y为

式中：Yi为个体的适应度值；x（1），x（2）分别为所选变压器的台数和容量；A为从MATLAB GUI操作界面输入的具体工程建筑面积的大小。

2.4 终止条件

算法达到遗传操作的迭代次数，即满足终止条件，程序输出最优解。遗传算法求解变压器年运行费用模型的流程如图5所示[16]。

2.5 可视化实现

本文采用MATLAB GUI实现系统的可视化设操作，显示界面见图6所示。界面左端是基于负荷曲线的建筑物变压器优化选择的输入参数，包括建筑面积和建筑类型；界面右端为系统的输出参数；界面下端为运行和清除两个按钮，点击运行按钮，输出变压器的台数、额定容量和年运行费用值。

图5 遗传算法求解变压器年运行费用模型流程Fig.5 Flowchart of the optimal transformer annual operating cost model based on GA

图6 Matlab GUI界面Fig.6 Matlab GUI interface

3 算例分析

3.1 算例参数

由上述可知，若已知某工程的建筑面积和建筑类型，就可以选出该工程建筑供配电设计中的变压器的台数和容量，得出变压器的年运行费用值。本文从南昌市某建筑设计研究院选取办公建筑、住宅建筑、商业建筑的设计验证模型的准确性和求解算法的有效性。每种建筑类型分别选取3组建筑物，其参数见表1所示。遗传算法参数设置如下：种群规模为100，迭代次数为100，交叉概率为0.6，变异概率为0.01。

表1 建筑物参数表Tab.1 Building data sheet

3.2 算例仿真

本文建筑物变压器选用10 kV级SCB10环氧树脂浇注干式变压器[17]，额定容量及其技术参数如表2所示。通过MATLAB软件对办公建筑中办1进行仿真，得到结果如图6所示，变压器的台数为2，额定容量为1 000 kVA，年运行费用为62.997 2万元。因此，该工程选取2台额定容量为1 000 kVA SCB10环氧树脂浇注干式变压器，详细参数见表2所示。

另外，结合相关资料，利用建筑供配电设计中的需用系数法对办 1进行负荷计算，总负荷容量为2 644.6 kW，负荷计算表如表3所示。由表3可以看出，该工程选取2台额定容量为1 600 kVA SCB10环氧树脂浇注干式变压器，详细参数见表2所示。

表2 SCB10环氧树脂浇注干式变压器技术参数表Tab.2 Technical data sheet of SCB10 epoxy cast dry-type transformers

同理，用上述两种方法分别对表1中的办公建筑、住宅建筑和商业建筑进行仿真计算，所得结果如表4所示。由表4可以看出，相同类型的同一建筑物，基于负荷曲线法所选变压器的容量相对较小；从变压器的年运行费用来看，基于负荷曲线法所选变压器的年运行费用值较低，减少了不必要的经济投入，实现经济性和节能性的优化选择。此外，基于负荷曲线的建筑物变压器的优化选择，只需要根据建筑物的建筑类型，输入其建筑面积的大小，就可以选出其建筑供配电设计中变压器的台数和容量，较需用系数法在一定程度了节省了大量的时间，提高了效率。考虑负荷的特性和变化规律建立变压器的年运行费用模型很有意义的。

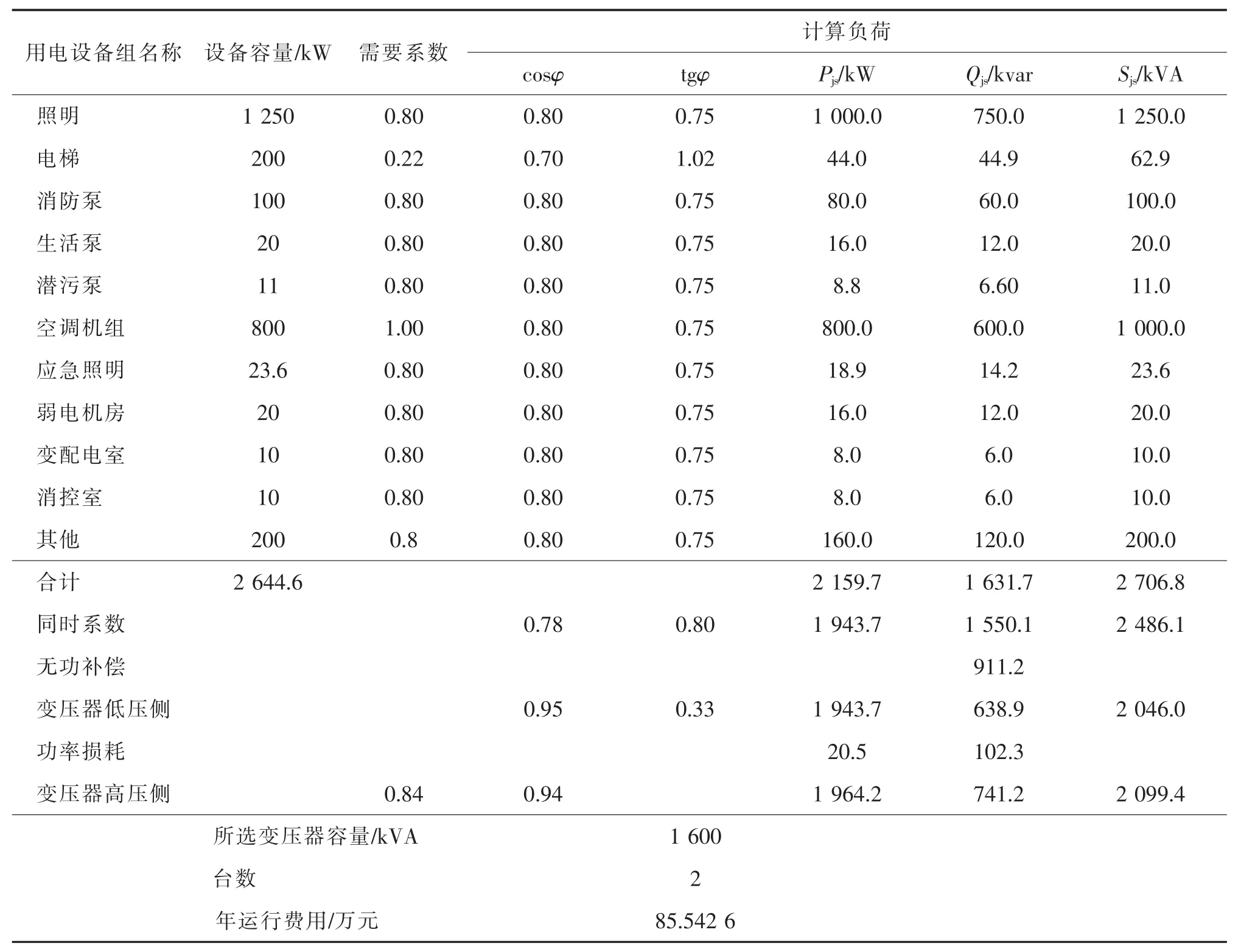
表3 电气负荷计算表Tab.3 Electric load calculation sheet

表4 2种方法结果比较Tab.4 Result comparison of the two methods

4 结论

考虑变压器的经济性，建立变压器年运行费用数学模型，并采用遗传算法求解模型，得到了综合投资最优的方案。本文的数学模型能够选择出方案最优的建筑物变压器，适用于当前推动智能建筑供配电的发展趋势，主要创新如下：

1）充分考虑负荷的特性和变化规律，提出了基于负荷曲线的建筑物变压器优化选择方法，与传统设计中根据供配电计算负荷，利用经验公式选择变压器相比，准确高效。

2）基于负荷曲线变压器的优化选择，其所选变压器的年运行费用值小于传统设计中变压器的年运行费用值，节省了投资，满足变压器年经济估值要求，是适应未来智能建筑供配电发展趋势的设计方法。

在本文研究的基础上，可进一步研究智能电网中智能建筑供配电的设计，包括电气信息的采集、数据通信以及远程控制等，通过优化算法，对系统三相平衡、短路保护、电能管理等关键技术进行深入研究，实现建筑供配电系统功能与安全管理的一体化，为供配电系统的安全可靠运行提供更充分的理论基础。

[1]任元会，卞铠生，姚家伟，等.工业与民用配电设计手册[M].北京：中国电力出版社，2005：41.

[2]谢静波.配电变压器容量的选择与运行[J].沿海企业与科技，2009（1）：25-26.

[3]王正风.变压器的容量选择与经济运行[J].变压器，2006，43（3）：30-32.

[4]刘照林.浅谈配电变压器经济容量选择方法及其应用[J].山西电子技术，2013（4）：38-39.

[5]曹阳.配电变压器容量选择方法探讨[J].沈阳工程学院学报：自然科学版，2010，6（1）：51-53.

[6]沈景霆.配电变压器容量选择与运行经济性问题[J].建筑电气，2002，21（4）：18-20.

[7]李逢元.住宅用电负荷分析[J].建筑电气，2011，30（3）：19-23.

[8]LEAL AG，JARDINI JA，MAGRINI LC，et al.Distribution transformer losses evaluation：a new analytical methodology and artificial neural network approach[J].IEEE Transactions on Power Systems Pwrs，2009，5（2）：705-712.

[9]陈校.某办公楼配电变压器选择及技术经济评价[J].智能建筑电气技术，2014，8（5）：75-80.

[10]黄烈江，平伟军.基于综合评价指标的电力变压器选型方法研究[J].浙江电力，2014（5）：11-16.

[11]中华人民共和国住房和城乡建设部.GB 50052-2009供配电系统设计规范[S].北京：中国计划出版社，2009.

[12]刘思亮.建筑供配电[M].北京：中国建筑工业出版社，2011：15.

[13]傅军栋，喻勇，刘晶.低压配电网三相不平衡节能算法研究[J].华东交通大学学报，2014，31（3）：110-114.

[14]占自才.基于遗传算法的PID智能控制器设计[J].华东交通大学学报，2009，26（1）：58-61.

[15]周明，孙树栋.遗传算法原理及应用[M].北京：国防工业出版社，2001：18-64.

[16]史峰，王辉，胡斐，等.MATLAB智能算法30个案例分析[M].北京：北京航空航天大学出版社，2011：17-19.

[17]中华人民共和国住房和城乡建设部.GB 50053-2013 20 kV及以下变电所设计规范[S].北京：中国计划出版社，2013.

Optimal Selection of Building Transformer Based on Load Curve

Fu Jundong1,Li Jianghui1,Zhang Yang2
（1.School of Electrical and Automation Engineering,East China Jiaotong University,Nanchang 330013,China;2.Jiangxi Province Architectural Design&Research General Institute,Nanchang 330046,China）

Considering the economy of transformer，a mathematical model of annual operating cost is established. With the minimum electric energy loss costs,basic power charges of transformer,depreciation expense of equipment investment and maintenance costs as the objective function,based on load curve of different types of buildings,a genetic algorithm is developed to work out the number and relative capacity of transformers in the building.Through the analyses of examples,the accuracy of the above model and the effectiveness of the algorithm have been verified.

building;load curve;genetic algorithm;transformer selection

TM421

A

1005-0523（2017）02-0134-09

（责任编辑 刘棉玲）

2016－09－22

傅军栋(1972—)，男，副教授，硕士生导师，主要研究方向为电力系统、建筑电气及智能化研究。

李江辉(1991—)，男，硕士研究生，研究方向为电力系统及其自动化。