螺纹深度和螺距对螺纹连接强度影响的有限元分析
2017-04-15涂文兵何海斌王筱鑫邹银辉周浩浩
涂文兵,何海斌,王筱鑫,邹银辉,周浩浩
(华东交通大学机电与车辆工程学院,江西 南昌330013)
螺纹深度和螺距对螺纹连接强度影响的有限元分析
涂文兵,何海斌,王筱鑫,邹银辉,周浩浩
(华东交通大学机电与车辆工程学院,江西 南昌330013)
螺纹连接是机械工业常用的零件连接方式,其强度对于保证零件连接关系的可靠性有着重大影响。为研究螺纹连接强度的影响因素,建立了3种不同螺纹深度和3种不同螺距以及3种不同载荷下的螺栓-螺母螺纹连接的有限元模型。从螺纹牙根部应力和螺栓轴向变形两方面分析了螺纹深度、螺距和载荷对螺纹连接强度的影响。结果表明,螺纹牙根部应力与螺纹深度、螺距皆成反比关系,而其与轴向变形均跟载荷成正比关系,为提高螺纹连接强度提供了一定的理论基础。
螺纹连接;螺纹深度;螺距;载荷;应力
螺纹连接是应用极为广泛的机械连接,其连接强度直接决定了整机的寿命与安全性。随着各类机械对可靠性要求的不断提高,对螺纹连接的接触应力分析提出了更高的要求。
KENNY等[1]采用光弹试验法通过多条纹偏光镜和记录式显微密度计获得了M30螺纹副的承载分布,且试验结果与SOPWITH理论解、有限元结果吻合良好。尹益辉等[2]采用有限元数值模拟的方法计算分析了普通螺栓-螺母副在轴向力作用下的内力、应力和变形规律。段巍等[3]对螺纹连接进行了有限元建模和计算,分析并比较了不同载荷和不同旋合扣数螺纹牙的应力分布、轴向弹塑性变形和接触面间的压力等方面。唐倩等[4]建立了挂载起吊系统力学模型和进行了相关实验,并运用有限元法对系统进行计算,得出了特种螺栓应力分布及系统各部件之间接触面积关系,且仿真结果与实验结果吻合良好,同时分析了螺栓预紧力、圆筒重力载荷对螺栓强度的影响。陈海平等[5]建立了参数化的螺纹副承载分布有限元模型,分析了螺纹类型、螺距、螺纹副径向尺寸系数、啮合扣数、摩擦因数和螺纹副材料弹性模量比等因素对螺纹副承载分布的影响。缪宏等[6]采用Yamamoto方法分析计算获得了各啮合螺纹的应力分布,并建立了连杆插销螺栓连接的有限元模型,分析了啮合螺纹的应力应变场以及冲击载荷对螺旋效果和螺纹啮合位置的影响。Chen等[7]基于弹性力学提出了一种可计算圆柱管螺纹连接的螺纹齿上载荷分布的分析方法,并通过有限元分析方法验证其正确性。Yang等[8]建立了螺栓连接的螺旋线三维有限元模型,发现模型的螺纹载荷分布吻合陈钬檚光弹试验结果。安晓卫等[9]建立了轴对称容器有限元模型及等距直螺纹,考虑螺纹升角的螺旋线螺纹的有限元子模型,计算分析了两种螺纹子模型的应力分布。倪佩韦等[10]建立了螺栓联接的三维有限元模型,依据Yamamoto解析法分析了螺纹牙的变形并计算了螺栓内外螺纹的应变,对螺纹副承载力分布进行模拟分析并与解析值进行对比,验证了模型的有效性。张倩等[11]提出了一种模拟盲孔、通孔螺栓连接的有限元仿真方法,利用分步加载技术模拟主螺栓预紧及加压过程中主构件的应力场和位移场情况,获得了螺栓受拉伸、剪切的危险截面所在位置。但以往大多数学者对螺纹的研究主要集中在螺纹连接的应力分布状况和变形情况,以及螺纹类型、螺纹扣数、摩擦系数和材料等因素对螺纹连接强度的影响等方面,极少研究不同螺纹深度、螺距和载荷对螺纹连接强度的影响。
以M36螺栓为研究对象,应用ANSYS建立螺栓螺纹连接静力学有限元分析模型并进行求解分析。从螺纹深度、螺距和工作载荷三方面进行研究,分析了螺纹深度、螺距和工作载荷对螺纹牙根部应力集中的影响,为提高螺纹连接强度提供了一定的理论基础。
1 有限元模型
1.1 螺栓几何参数
以M36螺栓为研究对象,其主要的几何参数如表1所示。
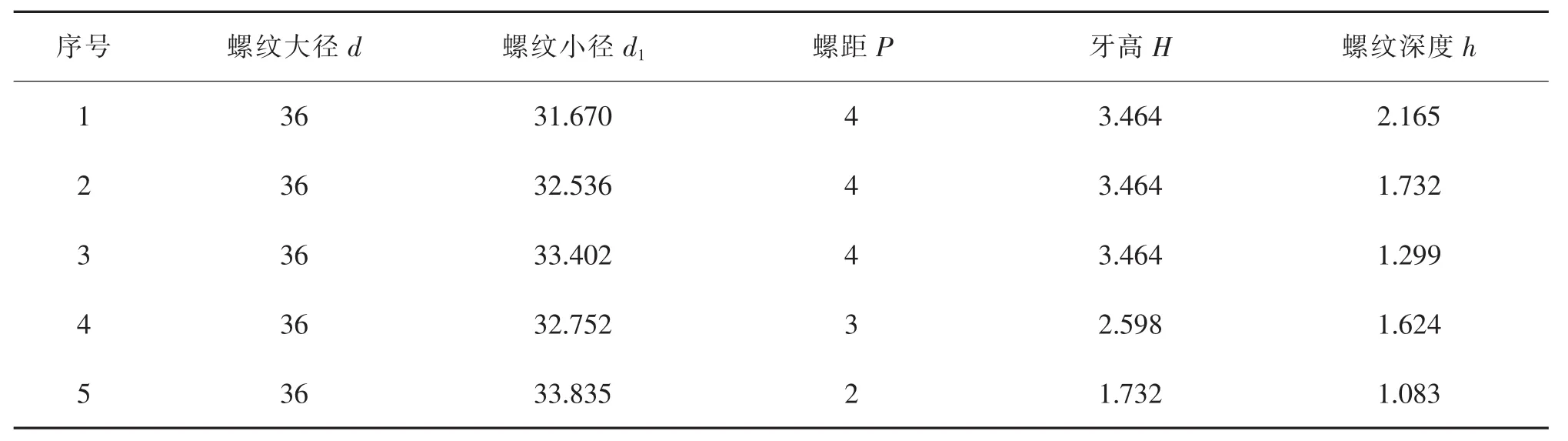
表1 螺纹连接分析几何参数Tab.1 Geometrical parameters of threaded connection mm
1.2 单元类型、材料选择与网格划分
螺纹副2D模型与3D模型的计算结果基本吻合,验证了2D轴对称模型用于求解螺纹副载荷分布的可靠性[12]。因不考虑螺纹升角时,螺栓与螺母的装配模型是轴对称模型,为控制有限元模型规模并有利于提高计算精度,本文采用四边形单元对2D模型进行自由网格划分;对螺栓和螺母的螺纹连接部分采用较密的网格;通过不断调试网格大小,观察计算结果的变化,若螺栓与螺母的螺纹牙根部应力变化控制在5%以内,则认为单元大小满足静力学求解要求。螺栓和螺母单元类型采用等参轴对称的Solid Quad 8node 82。
螺栓和螺母均采用300M高强度钢材料,本文中的螺栓与螺母采用各向同性弹性模型,密度=7 830 kg/m3,弹性模量E=206 GPa,泊松比= 0.3,抗拉强度=1 220 MPa。
螺栓和螺母的螺纹连接有限元模型如图1所示,由3 741个单元和11 255个节点构成。
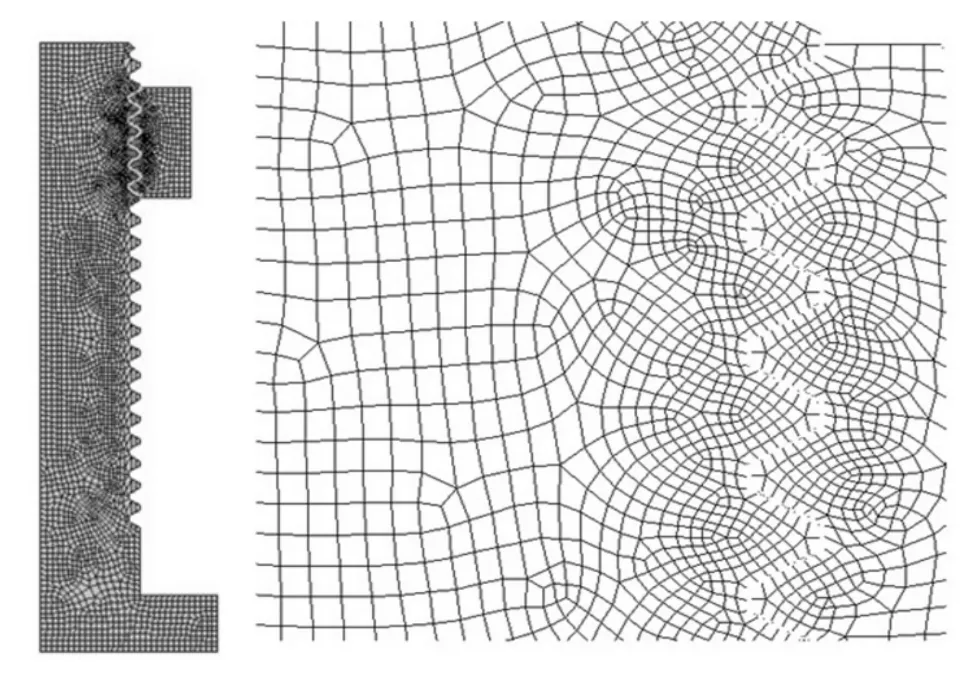
图1 螺纹连接有限元模型Fig.1 FEM model of the Threaded Connection
1.3 边界条件的设置
一般情况下,螺栓、螺母分别与待连接件的接触面受到方向相反的力;因此可对螺母与待连接件的接触面施加固定约束,对螺栓头部与待连接件的接触面施加轴向载荷,其大小为F=4 kN,平均分配在28个节点上。
在定义螺栓与螺母的接触时,要避免在初始状态下产生接触,选用2D接触单元TARGE169、CONTA172,摩擦因数为0.1。
2 计算结果与分析
2.1 模型验证
螺栓危险截面拉伸应力的理论计算公式为

式中:F为工作拉力,N;d1为螺栓危险截面的直径,mm;σ为拉伸应力,MPa。
由有限元法得,螺纹牙根部应力为9.813 MPa,即小径截面上最外侧应力,小径截面中心处应力为0.817 MPa,又因材料在屈服极限内可认为截面上的应力成线性分布,所以螺纹小径截面上的平均应力为5.315 MPa。螺栓连接拉伸应力的有限元解与解析解的结果对比如表2所示,其中,解析解通过公式(1)计算。

表2 螺栓连接静力学参数对比Tab.2 Comparison of statics parameters
结果表明,有限元解与解析解相对误差为4.67%,吻合良好,说明本文利用有限元法求解螺纹连接应力的有效性。
2.2 螺纹深度对螺纹连接强度的影响
3种不同螺纹深度螺纹连接的应力分布及螺纹牙根部最大应力分别如图2和表3所示。从图2和表3中的数据可知:h1=2.165 mm螺栓连接的最大应力出现在第一圈螺纹牙根部上,h2=1.732 mm和h3=1.299 mm螺栓连接的最大应力出现在螺母的端面上,表明螺纹深度会影响螺纹连接的应力分布形式。螺纹深度越小的螺纹连接,其应力比较集中,说明减小螺纹深度可能导致螺纹连接承载不均匀。当螺纹深度值最大时,螺纹牙根部最大应力为最小,当螺纹深度值最小时,螺纹牙根部最大应力为最大,表明螺纹深度对螺纹连接的螺纹牙根部应力影响很大,且二者成反比关系,这是因螺纹深度值变小会减小螺纹连接的有效接触面积引起的。

图2 不同螺纹深度螺纹连接的应力分布Fig.2 Stress distribution of threaded connection under different thread depth

表3 不同螺纹深度螺纹连接的螺纹牙根部最大应力Tab.3 Maximum stress on thread root at different thread depth
螺纹连接上的位置标识及不同螺纹根部位置处应力分别如图3和图4所示。从图4可知:螺纹连接的螺纹牙根部最大应力出现在第一圈螺纹上且比其它各圈大的多,最后几圈螺纹所受的螺纹牙根部最大应力相差不大,说明最大接触载荷出现在第一圈螺纹牙上,这是由于螺纹螺距变化差以旋合的第一圈为最大,后面逐圈递减,说明采用螺纹牙圈数过多的厚螺母并不能提高螺纹的连接强度。
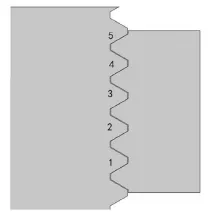
图3 螺纹连接上的位置标识Fig.3 Location logo of threaded connection

图4 h1=2.165 mm螺纹连接不同螺纹牙根部位置处应力Fig.4 Stress on different location of thread root when h1=2.165 mm
2.3 螺距对螺纹连接强度的影响
3种不同螺距的螺纹连接应力分布及螺纹牙根部最大应力分别如图5和表4所示。从图5和表4中的数据可知:P1=4 mm螺栓连接的最大应力出现在啮合的第一圈螺纹的螺栓上,P2=3 mm和P3=2 mm螺栓连接的最大应力出现在啮合的第一圈螺纹的螺母上。当螺距越小时,螺纹连接应力分布扩展至螺纹圈数越多,但应力分布范围则越小,这是因螺纹牙根部变薄易产生弯曲变形引起的,表明螺距对螺纹连接的应力分布形式影响较大。螺距最大螺纹连接的螺纹牙根部最大应力最小,螺距最小螺纹连接的螺纹牙根部最大应力最大,表明螺距越大的螺纹连接的螺纹牙根部应力越小,这是由于在螺纹连接轴向啮合长度相同状况下,因螺距变小使得螺纹牙高减小,进而使得螺纹连接的有效接触面积减小而造成应力分布变得更集中,从而增大接触面上的应力及螺纹牙根部的应力。
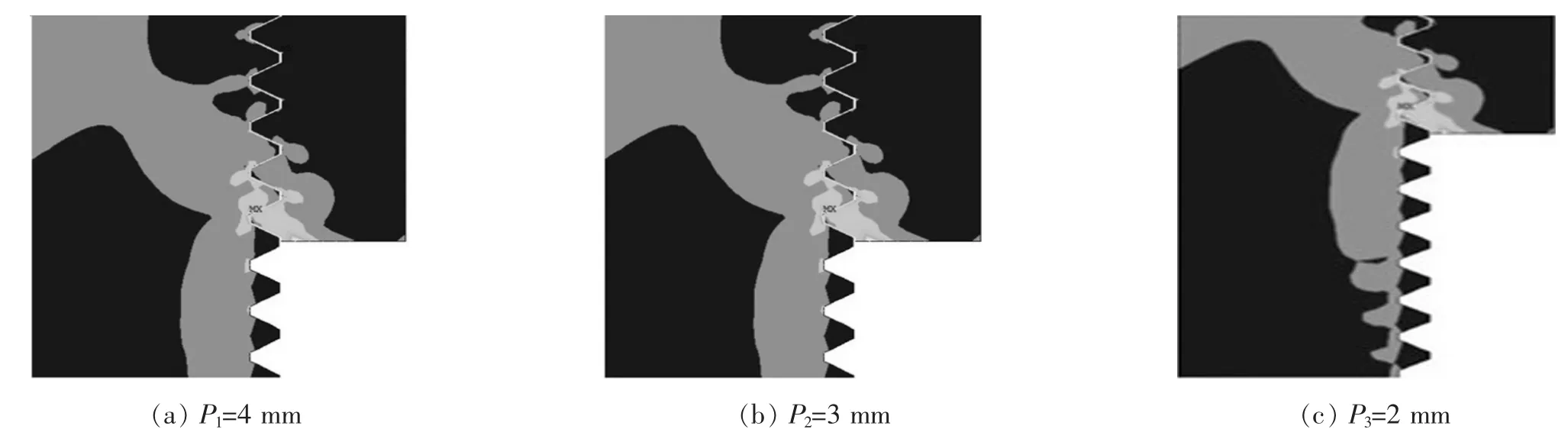
图5 不同螺距螺纹连接的应力分布Fig.5 Stress distribution at different threadpitch

表4 不同螺距螺纹连接的螺纹牙根部最大应力Tab.4 Maximum stress on thread root at different threadpitch
2.4 载荷对螺纹连接强度的影响
3种不同集中拉力载荷下螺纹连接的应力分布、轴向变形及螺纹牙根部最大应力分别如图6和表5所示。
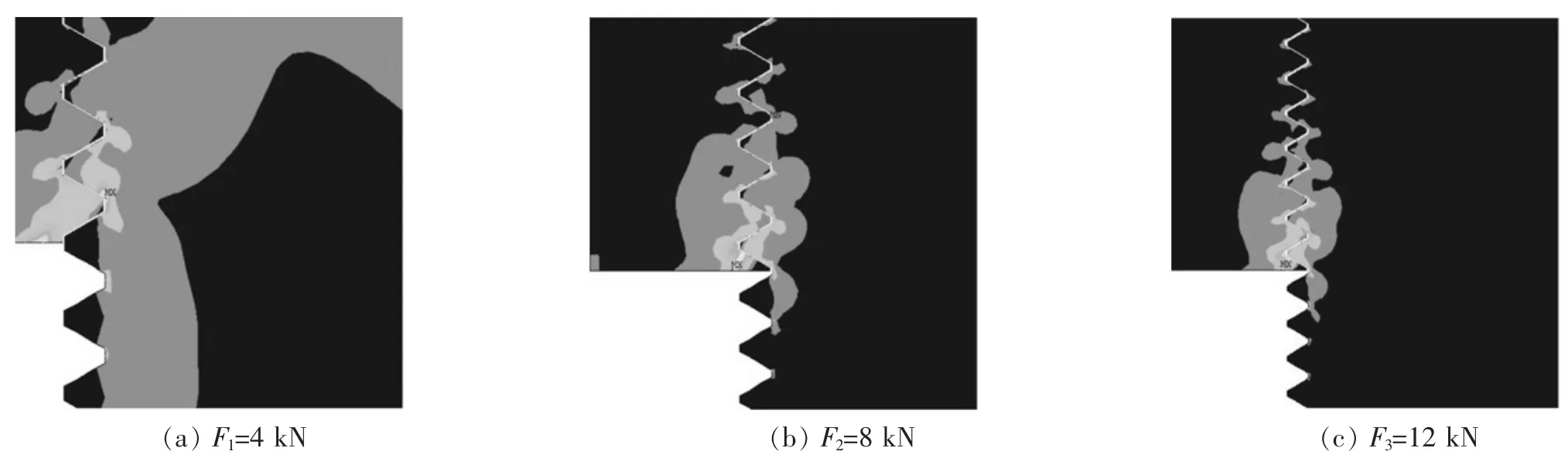
图6 不同载荷下螺纹连接的应力分布Fig.6 Stress distribution at different loads

表5 不同螺距螺纹连接的螺纹牙根部最大应力Tab.5 Maximum stress on thread root at different threadpitch
从图6和表5中的数据可知:螺纹连接处的应力由螺纹牙根部向四周逐渐扩展且应力值逐渐减小,出现最大应力的螺纹圈数随工作载荷的增大而增多。螺纹牙根部最大应力出现在啮合的第一圈螺纹上,并且其出现位置不随工作载荷大小的改变而发生变化。螺纹连接的轴向变形的最大值出现在螺栓头部而不是螺纹连接处,并且随着距螺栓头部距离的增大而逐渐减小,其变形趋势一致,不受工作载荷的影响。F2=8 kN时的螺纹牙根部最大应力值和最大轴向变形均接近F1=4 kN时的2倍,F3=12 kN时的螺纹牙根部最大应力及最大轴向变形都约为F1=4 kN时的3倍,说明在螺纹连接的屈服极限内,螺纹牙根部应力及轴向变形与工作载荷成正比关系。
3 结论
以M36螺栓为研究对象,建立了3种不同螺纹深度螺栓连接和3种不同螺距螺栓连接以及3种不同载荷下螺栓连接的有限元分析模型,从螺栓的螺纹牙根部应力和轴向变形两方面分析了螺纹深度、螺距和载荷螺纹连接强度的影响,主要结论如下:
1)解析解与有限元解吻合良好,表明本文螺纹连接有限元模型是有效的。螺纹连接的最大等效应力出现在第一扣螺纹牙根部,越往后的螺纹所受应力越小,说明采用螺纹牙圈数过多的厚螺母并不能提高螺纹的连接强度。
2)螺纹深度越大,螺栓螺纹牙根部应力则越小,表明螺纹连接的螺纹牙根部应力与螺纹深度成反比关系。
3)螺距越小,螺栓螺纹牙根部应力反而越大,说明螺距过小会导致螺纹连接的螺纹牙根部应力更集中。
4)工作载荷成倍增加时,螺栓的螺纹牙根部应力和轴向变形也按相同倍数增大,表明螺纹连接的螺纹牙根部应力及轴向变形均与工作载荷成正比关系。
[1]KENNY B,PATTERSON E A.Load and stress distribution in screw threads[J].Experimental Mechanics,1985,25(3):208-213.
[2]尹益辉,余绍蓉.螺栓啮合螺纹段的轴力、等效应力分布及摩擦的影响分析[J].机械强度,2006,28(4):146-147.
[3]段巍,温新林,唐贵基,等.不同旋合扣数下钢拉杆螺纹联接强度试验及有限元应力分析[J].机械强度,2008,30(5):823-828.
[4]唐倩,裴林清,陆波.大型挂载起吊系统特种螺栓强度分析[J].重庆大学学报,2009,32(9):1028-1031.
[5]陈海平,曾攀,方刚,等.螺纹副承载的分布规律[J].机械工程学报,2010,46(9):171-178.
[6]缪宏,左敦稳,汪洪峰,等.冲击载荷对飞机起落架螺纹连接的影响[J].振动与冲击,2010,29(2):208-211.
[7]CHEN S J,AN Q,ZHANG Y,et al.Loading analysis on the thread teeth in cylindrical pipe thread connection[J].Journal of Pressure Vessel Technology,2010,132(3):1-8.
[8]YANG G,HONG J,Zhu L,et al.Three-dimensional finite element analysis of the mechanical properties of helical thread connection[J].Chinese Journal of Mechanical Engineering,2013,26(3):564-572.
[9]安晓卫,李丽,刘修亚.基于有限元子模型的特种容器螺纹强度分析[J].机械强度,2013(6):816-822.
[10]倪佩韦,王胜春,张烨.基于三维有限元模型的螺纹副承载力分布研究[J].起重运输机械,2015(10):33-37.
[11]张倩,刘义.基于有限元方法的压力容器螺栓连接强度分析[J].机械制造,2016,54(4):37-40.
[12]ZHAO HUA.A numerical method for load distribution in threaded connections[J].Journal of Mechanical Design,1996,118(2):274-279.
[13]魏斯亮,李时骏,唐小青.一种大导程联结螺纹的加工[J].华东交通大学学报,2002,19(2):39-41.
FEM Analysis of the Effect of Thread Pitch and Depth on Strength of the Threaded Connection
Tu Wenbing,He Haibin,Wang Xiaoxin,Zou Yinhui,Zhou Haohao
(School of Mechatronics and Vehicle Engineering,East China Jiaotong University,Nanchang 330013,China)
The threaded connection is a common parts connection in mechanical industry,and its connection strength has great influence on the reliability of the parts connection relationship.To study the influence factors of the strength of threaded connection,the finite element models of bolt-nut thread connection withthreetypes of thread depth,threetypes of pitch and threetypes of load were established.The influence of the thread depth, pitch and loading on the strength of threaded connection was analyzed from the stress of thread root and the axial deformation of bolt.The results showed that the thread root stress is inversely proportional to the thread depth and pitch,and the bolt axial deformation has direct ratio relations with loading,which provides theoretical basis for improving the strength of threaded connection.
threaded connection;thread depth;pitch;load;stress
U463.55
A
1005-0523(2017)02-0118-06
(责任编辑 刘棉玲)
2016-10-26
江西省自然科学基金项目(20151BAB216017,20161BAB206151)
涂文兵(1983—),男,讲师,博士,主要研究方向为有限元分析与机械系统动力学。
