经济FMEA模型在覆土滚筒生产质量缺陷识别中的应用

侯晓晓+赵永满++胡斌

摘要：覆土滚筒半轴同轴度影响覆膜播种机的铺膜平整性、覆土道一致性和滾筒滚动平稳性，识别半轴同轴度超差的关键来源是改善覆土性能的首要任务。在传统缺陷模式及影响分析（failure mode & effect analysis，FMEA）法的基础上提出新的风险因子——经济度（economy，E），制定其评价等级，并采用模糊置信结构和灰色关联投影法对潜在缺陷来源（焊接变形、螺栓紧固变形、翻边圈圆度超差、调节圈圆度超差、中间固定圈圆度超差和中间固定圈总成同轴度超差）的风险因子评价信息进行处理，从质量和成本2个方面综合评估缺陷风险，得到焊接变形是造成覆土滚筒左右半轴同轴度超差的关键来源，研究结果对我国农机生产质量改进有一定参考价值。

关键词：覆土滚筒；半轴同轴度超差；经济FMEA；模糊证据推理；灰色关联投影

中图分类号： S220 文献标志码： A

文章编号：1002-1302（2017）05-0207-04

地膜覆盖栽培技术在干旱和半干旱地区得到广泛应用，覆膜播种机的覆土部件——覆土滚筒用于膜上种孔覆土，滚筒表面从地膜上滚动过去时将覆土圆盘导入滚筒的土壤覆压在地膜上，确保地膜不被风吹起。左右半轴是覆土滚筒的重力支点和回转中心，两者的同轴度直接影响覆土机构的运动稳定性和覆土道的整齐性，因此识别半轴同轴度超差关键缺陷来源对提高覆土性能具有重要意义。

FMEA法通过评价缺陷来源的严重度、发生度、检测度得到风险优先指数，继而识别缺陷关键原因，广泛应用于食品、环境、医疗、汽车等行业[1-4]。传统FMEA法虽应用广泛，但存在诸多问题：（1）无法准确表达风险因子信息的多样不确定性；（2）专家打分主观性强；（3）忽略因子对缺陷的相对权重；（4）忽略成本风险。针对以上问题，国内外学者对FMEA法作了改进。在质量风险评估方面，部分学者将模糊置信结构、D数理论、证据推理理论、灰色关联理论等技术应用到FMEA模型中，同时考虑专家权重和风险因子相对权重，实现了大量不准确信息的量化和潜在缺陷风险排名优化[1-9]。在成本风险评估方面，Gilchrist以缺陷数目和平均缺陷成本为因子，提出基于预期成本模型，更加经济实用[10]。Ben-Daya等对Gilchrist提出的模型[10]进行修正[11]。Rhee等提出以工时成本、材料成本和机会成本衡量风险，并制定改善措施[12-13]。

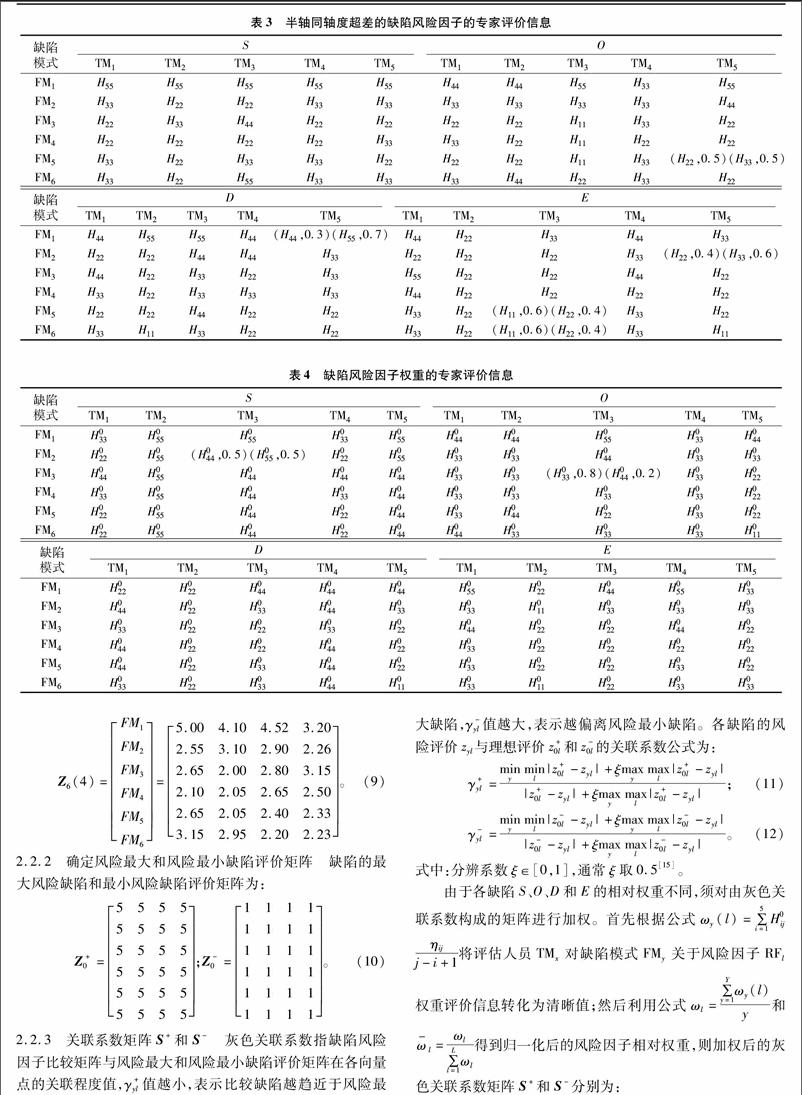
以上研究未综合考虑缺陷质量风险和成本风险。本研究提出基于质量和成本的经济FMEA法，该方法将项目生命周期内的产出与投入比定义为经济度E，作为第4个风险因子，并以覆土滚筒为研究对象，采用模糊置信结构和灰色关联投影法对其潜在质量缺陷（焊接变形、螺栓紧固变形、翻边圈圆度超差、调节圈圆度超差、中间固定圈圆度超差和中间固定圈总成同轴度超差）的风险因子评价信息进行处理，识别半轴同轴度超差的关键缺陷来源。

1经济度及其评价等级

1.1经济度E

定义经济度E为产品生命周期内的最终产出与所投生产要素总成本的比值。投入成本包括建设期投入总成本和生产期投入总成本，则经济度公式为：

[JZ（]E=[SX（]O1I0+I[SX）]。[JZ）][JY]（1）

式中：I0为建设期生产要素投入总成本；I为生产期要素投入总成本；

3结论

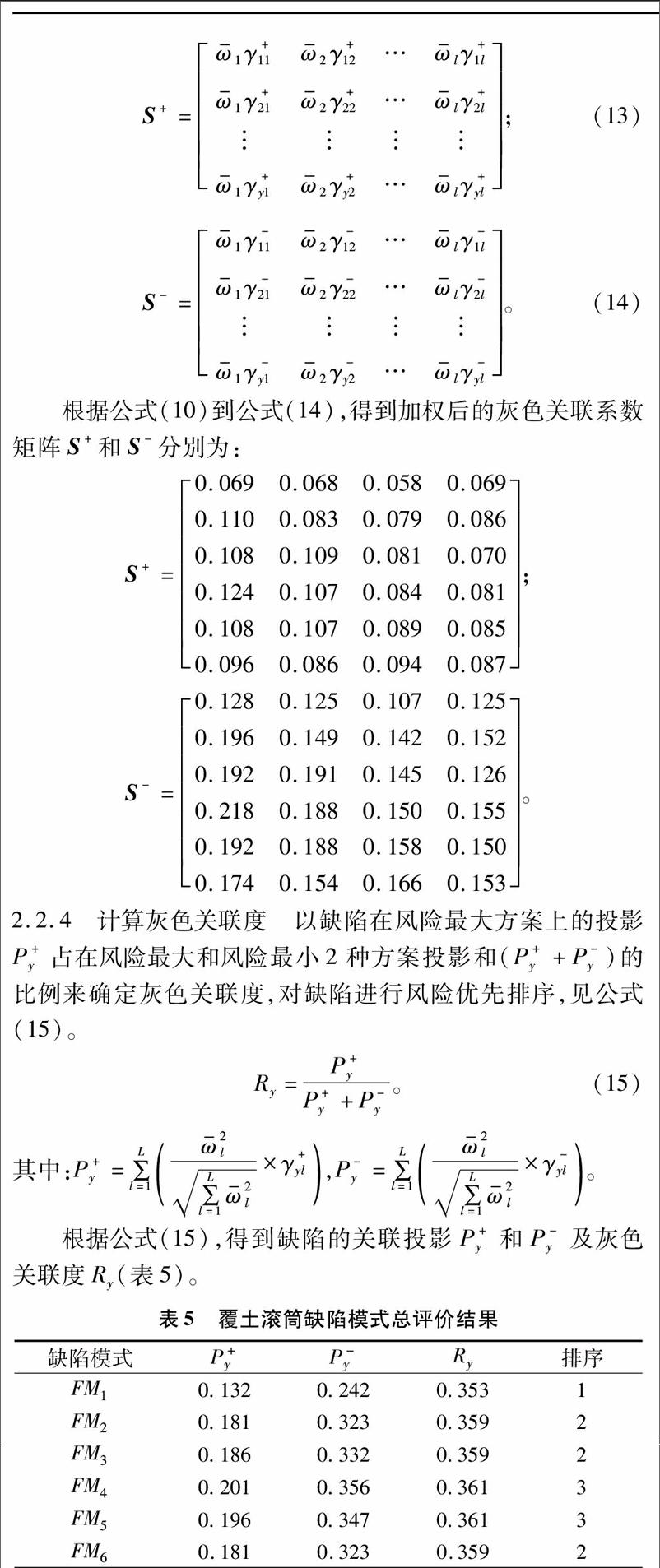
基于过程质量和成本2个方面风险考虑，继S、O和D之后引入E，提出了包含4个风险因子的经济FMEA法。利用该方法，根据覆土滚筒同轴度超差历史数据和专家打分，通过计算焊接变形、螺栓紧固变形、[JP2]翻边圈圆度超差、调节圈圆度超差、中间固定圈圆度超差和中间固定圈总成同轴度超差等6个缺陷的RPN值，科学准确地识别危害最大的缺陷，即焊接变形严重。与传统模型相比，该模型具有以下特点：（1）采用模糊置信结构准确表达半轴同轴度超差来源评价信息的不确定性、不完整性和多样性；（2）考虑各缺陷的风险因子权重；（3）利用各缺陷风险分别在风险最大方案和风险最小方案上的关联投影值对缺陷进行风险优先排序；（4）以S、O、D和E为风险因子，综合考虑质量风险和成本风险；（5）将E作为风险因子，为资金周转较难的中小型企业的质量控制提供参考。[JP]

参考文献：

[1]Bowles J B，Pelaez C E. Fuzzy logic prioritization of failures in a system failure mode，effects and criticality anaylsis[J]. Reliability Engineering and System Safety，1995，50（2）：203-213.

[2]Chin K S，Wang Y M，Poon G K K，et al. Failure mode and effects analysis using a group-based evidential reasoning approach[J]. Computers and Operations Research，2009，36（6）：1768-1779.

[3]Hadi-Vencheh A，Hejazi S，Eslaminasab Z. A fuzzy linear[JP3] programming model for risk evaluation in failure mode and effects analysis[J]. Neural Computing and Applications，2013，22（6）：1105-1113.[JP]

[4]门峰，姬升启. 基于模糊集与灰色关联的改进FMEA方法[J]. 工业工程与管理，2008（2）：55-59.

[5]刘胧，刘虎沉，林清恋. 基于模糊证据推理和灰色關联理论的FMEA方法[J]. 模糊系统与数学，2011，25（2）：71-80.

[6]Deng Y. D numbers：theory and applications[J]. Journal of Information & Computational Science，2012，9：2421-2428.

[7]Liu H C，You J X，Fan X J，et al. Failure mode and effects analysis using D numbers and grey relational projection method[J]. Expert Systems with Applications，2014，41 （10）：4670-4679.

[8]Du Y X，Mo H M，Deng X Y，et al. A new method in failure mode and effects analysis based on evidential reasoning[J]. International Journal of System Assurance Engineering and Management，2014，5（1）：1-10.

[9]Vahdani B，Salimi M，Charkhchian M. A new FMEA method by integrating fuzzy belief structure and TOPSIS to improve risk evaluation process[J].The International Journal of Advanced Manufacturing Technology，2015，77（1）：357-368.[ZK）]

[10]Gilchrist W. Modelling failure modes and effects analysis[J]. International Journal of Quality & Reliability Management，1993，10（5）：16-23.

[11]Ben-Daya M，Raouf A. A revised failure mode and effects analysis model[J]. International Journal of Quality & Reliability Management，1996，13（1）：43-47.

[12]Rhee S J，Ishii K. Using cost based FMEA to enhance reliability and serviceability[J]. Advanced Engineering Informatics，2003，17（3/4）：179-188.

[13]胡玺良，张代胜，刘焕广. 探析基于寿命成本的FMEA[J]. 现代机械，2007（1）：4-7.

[14]Liu H C，Liu L，Lin Q L. Fuzzy failure mode and effects analysis using fuzzy evidential reasoning and belief rule-based methodology[J]. IEEE Transactions on Realiability，2013，62（1）：23-36.

[15]Deng J L. Introduction to grey system theory[J]. Grey System，1989，1（1）：1-24.