人教版三种教材中“圆”的比较与思考

叶妙法

摘 要 本文以人教版1990年、2006年、2011年（新课标）的三种小学数学教材中“圆”的课程内容为研究对象，从内容呈现形式及顺序的视角出发，对“圆”的教材安排、教材结构、情境设计、概念得出、画圆技能、知识拓展等进行比较分析，并结合自己教学实践，阐释了对概念课教学的一些思考与想法。

关键词 圆 小学数学 人教版教材 比较

中图分类号：G623.5 文献标识码：A 文章编号：1002-7661（2017）07-0063-03

不同时期的小学课本，反映不同时代的教学理念。寻求不同时代背景下的教材特点，比较不同时期的教材编排，可以从一个侧面了解教学理念的变化过程，从中看到一些教学方式、学习方式、思维方式等諸多层面的进步与发展，为我们一线教师更好地使用教材起到积极的作用。现笔者选取人民教育出版社（以下简称“人教版”）1990年、2006年、2011年（新课标）出版的三种小学数学教材，对“圆”的课程内容进行比较分析。

一、“圆”的教材年级安排比较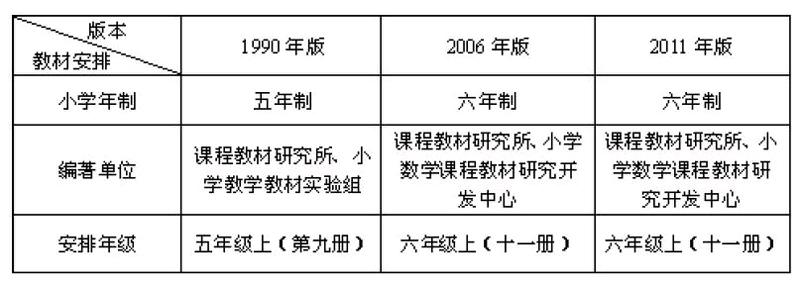

三个时期的教材把“圆”的教学都安排在小学的最后一年学习。之所以把“圆”的相关知识的学习放在最后一年学习，主要是考虑到有关圆的教学内容对学生来说有一定的难度，知识点也渗透了曲线图形与直线图形的关系，从空间观念方面来说，学生已经进入了一个新的领域，也是小学数学教学中的重难点。而且“圆的周长”、“圆的面积”对学生来说不容易想到化曲为直的过程，因此，根据学生的年龄特征安排在最后一年比较合理，这样相对来说学起来比较轻松，也可以为学习圆柱、圆锥等知识打好基础。

二、“圆”的教材结构比较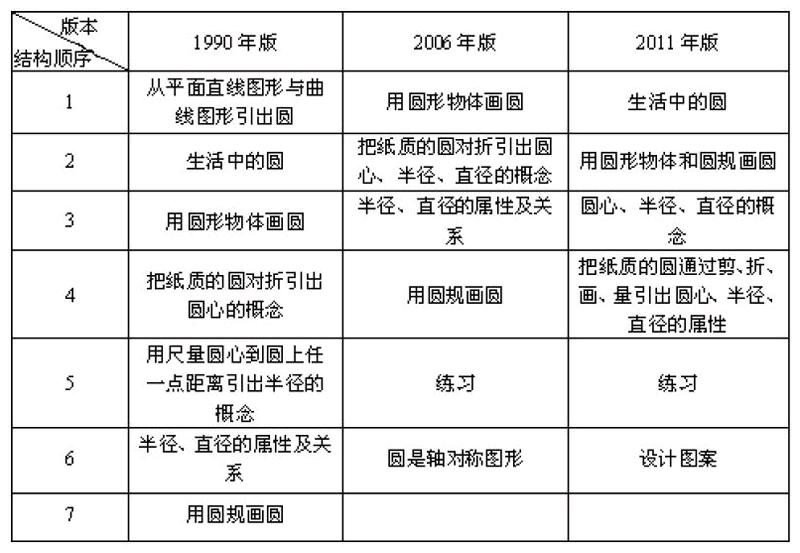

从上面三种教材的结构上看，在知识呈现的前后顺序大致一样，但也存在共同点与不同点。它们的共同点是：先画圆再给出圆的各部分名称，再进行半径、直径的属性与关系研究。不同点是：（1）1990年版与2011年版的教材在给出圆的各部分名称前，让学生回顾生活中的圆以及画圆，而2006年版的教材在给出圆的各部分名称之前，没有“生活中的圆”这一环节。（2）1990年版和2006年版的教材是在认识了圆的各部分名称、概念、关系后再“用圆规画圆”，而2011年版的教材把“用圆规画圆”和“用圆形物体画圆”结合起来作为学生探索的环节，并放在“认识圆的各部分名称”之前，这样的安排更注重解决问题策略的多样化以及注重探索的过程。

三、“圆”的情境设计比较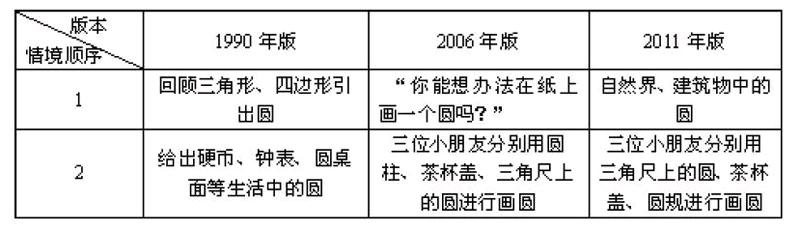

从三个不同版本的教材情境设计来看，它们都考虑到了“生活中的圆”，这样的情境比较符合学生的实际。不过它们也有不同点：（1）1990年版“生活中的圆”是直接用文字表现出来，教材上直接写着“我们周围的物体有很多是圆形的。例如硬币、钟面、圆桌面等”，然后在文字下面附上三张图，而2006年版及2011年版就没有直接出现这样的文字，2006年版是在主题图中让学生通过画圆感受“生活中的圆”，2011年版是通过寻找生活中的圆和画圆两个情境来感受“生活中的圆”。（2）虽然三种版本都强调了圆是生活中常见的图形，但1990年版是通过与三角形、四边形等平面图形进行比较引出另一个平面图形圆，而2006年版和2011年版都强调学生自己去寻找发现生活中的圆，充分调动学生在生活中认识圆的经验。

四、“圆”的概念得出比较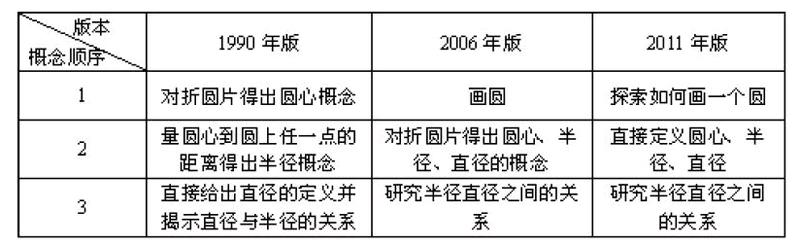

虽然三种都重视圆心、半径与直径这三个概念的发生过程，也在概念得出之前注重学生的活动过程，如1990年版的和2006年版的教材都让学生折一折，2011年版的教材让学生画一画，这样的活动设计为学生对概念的理解起到良好的保障作用。但它们的概念得出存在着较大的差异，1990年版的教材是操作得出圆心、半径的概念，直接定义直径概念，并着重探索半径与直径之间的关系；2006年版的教材是操作得出圆心、半径以及直径的概念，着重探索半径和直径之间的关系；2011年版的教材是直接定义圆心、半径、直径的概念，着重探索圆的画法及概念之间的关系。教材编排的改变是把“概念的探索”转变为“知识的探索”，更有利于学生探索与发现概念的本质与概念之间的联系。

五、“圆”的圆规画圆比较

1990年版的教材明确阐述了用圆规画圆的原理：根据圆上任意一点岙圆心的距离（即半径）都相等，而且十分明确地阐述了用圆规画圆的步骤及给出了相对应的图示；2006年版的教材以人物对话的形式给出了画圆的步骤，给出的图示相对比较简单；2011年版的教材对如何用圆规画圆没有给出详细的步骤，只是给出部分的暗示。教材这样的变化，或许是想让学生自己总结提炼出画圆的方法与步骤，而不是老师把步骤教给学生，体现学生的主体性与发展性。不过依笔者在教学中的经验，若在教学中最终形成如何用圆规画圆的步骤，会更加有利于学生掌握画圆的技能。

六、“圆”的知识拓展比较

这用运用圆规和直尺设计图案是一种很好的作业形式，一方面可以运用圆的知识，进一步熟练画圆的技能，另一方面可以培养学生的学习兴趣和创造精神，不过三中版本的拓展程度不同。首先从题目的要求来看，被打星号的练习题表示是选做题，并不要求所有的学生都掌握，所以2006年版的和2011年版的在作图要求上比1990年版的要高；2011年版的图案虽然比2006年版的少了一个，但篇幅增大，而且有详细的步骤，显然在表述一个数学问题时，2011年版的难度相对较低，学生容易解决。从这里看出，教材考虑到圆的相关知识拓展的广度与深度，设计的练习如何更有利于学生学习。

七、对“圆”的思考

通过对人教版不同版本教材中关于“圆”的内容整理、分析与比较，发现不管在哪个版本的教材中，“活动”是概念课教学的导入，“过程”即学习，最后在“图式”中获得概念，这样一个过程，就是我们平常概念课的一种常态教学环节，这样的环节为的就是让学生充分经历“概念的产生”、“概念的形成”、“概念的應用”整个过程，而这个过程笔者认为是数学思维的过程，要具有表象性、概括性、问题性的数学思维。

（一）概念课要具表象性

数学概念是事物本质属性的一种反映，它是一种客观事物的特征概括，所以有时需要明确的含义。如果学生对一些概念含义不明白，那么在他们解决问题时一定会遇到困难。因此让概念表象可以让学生直接作用于感觉器官，更加有利于对概念的理解。如1990年版的“圆”就有半径与直径关系的图式表象：d=2r或r=1/2d，2006年版与2011年版也是用字母d、r来表示。这样的字母、式子可以让学生对半径与直径的关系与公式的结构关系形成相一致的模式映象。

（二）概念课要具概括性

数学中很多概念是比较抽象的，如“同一圆内，所有的半径都相等，所有的直径都相等”这一结论概括，对于学生来说是将活动中直径与半径之间的联系推广到所有圆中去，这种思维概括与抽象互为表里的描述更需准确性，因此，我们要得出明确的概括性语言。1990年版的教材是以提问的形式：“在一个圆里，直径的长度与半径有什么关系？”而2006年版和2011年版的教材就明确用文字概括出：“同一圆内，所有的半径都相等，所有的直径都相等”，再让学生进一步想象、推理、感悟这一结论。

（三）概念课要具问题性

解决问题是数学思维活动的中心，美国数学家哈默尔莫斯指出：定理、证明、概念、定义、理论、公式、方法中任何一个都不是数学的心脏，只有问题是数学的心脏。概念的学习也是为了让学生更好地解决问题，所以概念课更应具有问题性。从2006年版和2011年版的教材来看，它们都有“你能在纸上画一个圆吗？”这样一个围绕问题展开的思维活动，三个版本也同时都有“设计美丽图案”的习题，表现为“发现问题—提出问题—分析问题—解决问题”的一般思维过程。

所以，概念课的教学要揭示或展现蕴含在知识里的本质，作为老师，我们要分析教学内容的特定含义，要分析教材编者的数学思维过程，要揭示教材编写者的具体意图。我们若能横向比较教材的安排，纵向比较教材的变化，努力读懂教材、用好教材，我们在教学上将会游刃有余。

参考文献：

[1]朱乐平. 圆的认识教学研究[M].北京：教育科学出版社，2013 .

[2]教育部.义务教育数学课程标准（2011版）解读[M].武汉：湖北教育出版社，2011.

[3]朱学尧.简单的设计，精彩的演绎——观潘小明老师的“圆的认识”一课[J].小学教学（数学版），2011，（04）.

（责任编辑 楚云鹏）