孪生素数及素数分布的思考

李科

摘 要 本文通过一种全新的思路，利用不能用“素数和”与“素数因子乘积”表示的整数即为素数的两种思路，将整数以双素数和与素数因子乘积的形式分别列入一个分布阵列表中，并通过观察发现素数及孪生素数的某些规律，并结合这些规律将孪生素数猜想的形式转变为“除了第一个整数所在的行，其他行必须有第2列，且有无穷多个整数在第2列换行”与“已知小素数乘积不能表示的整数即为素数”两种新形式。再结合素数性质分步证明孪生素數猜想。最后结合该表提出了两种新的寻找已知素数后下一个素数的方法。

关键词 素数 孪生素数 哥德巴赫猜想 数论 数学

中图分类号：O413 文献标识码：A 文章编号：1002-7661（2017）07-0001-03

素数是指除了1和它本身以外不会被其他任何整数整除（正因数只有1和其本身）的自然数。很明显，除了2都是奇数。“孪生素数”则是指两个相差为2的素数，例如3和5，5和7，2003663613195000-1和2003663613195000+1等。古希腊数学家欧几里得认为存在无穷多对相差2的素数，这就是孪生素数猜想（及存在无穷多素数P，使得P+2为素数）。与哥德巴赫猜想一样，未被公开证明。其弱形式是“对任何一个正数，有无穷多对素数之差小于这个给定的正数”，这个弱形式就如同哥德巴赫猜想中的“9+9”到“1+1”一样重要。但证明过程一波三折，至今未能将这个正数证明到2。本文主要介绍了一种证明思路，或许不尽正确，但也不失为另辟蹊径的一道良方。

一、孪生素数的产生与进展

对于孪生素数的弱形式（波利尼亚克猜想），1966年陈景润利用筛法证明了存在无穷多个素数p，使得p+2要么是素数，要么是两个素数的乘积。虽然开了一个头，但后来很长一段时间没人超越，这与证明方法有关。直到2013年张益唐取得的突破性进展，他在不依赖未经证明推论的前提下证明存在无穷多个之差小于7000万的素数对，这虽然与2相差甚远，但相比与正无穷的距离来说已经是微不足道的了。这是人类在证明孪生素数猜想上打开的第一扇窗户，随后在1个月内这个距离被不断刷新为6000万，4200万，1300万，500万，40万……到2014年2月该距离被缩短到了246。虽说距离2已是近在咫尺，可似乎却愈发觉得遥不可及。难道该方法如同筛法，也是双刃剑，在取得可喜进展的同时也埋下了不可跨越的鸿沟？为此作者通过研究孪生素数的规律，另辟蹊径，希望对该猜想的最终证明有所启示。

二、绕开陷阱，另辟蹊径

1.偶素的素数加和性质

为寻找良方证明孪生素数猜想，必须发现素数的一些未被发现或被人忽视的规律。为便于研究，绘制表1的素数表，每一行为一组质数，每列为连续偶数的素数加和式。为便于理解，该表引入了半数偏差概念（小的为负偏差，大的为正偏差），其偏差值N在数值上等于两个质数距离的一半。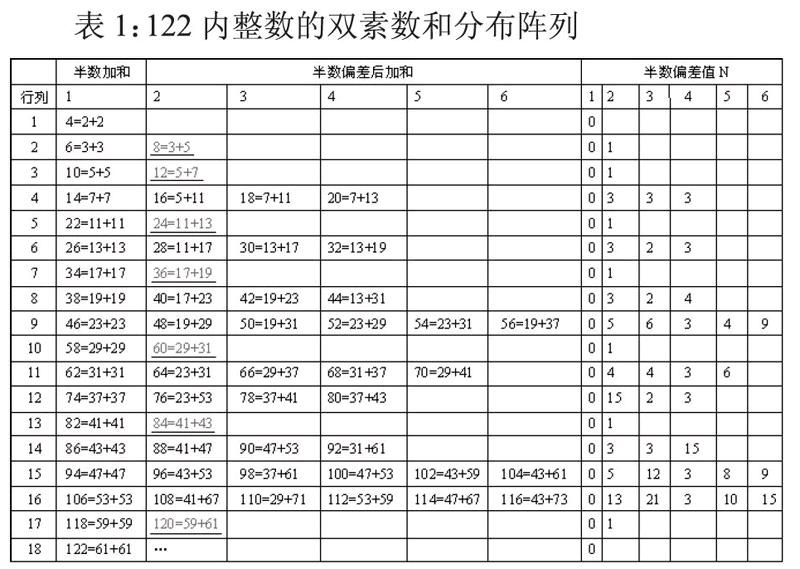

仔细观察，不难发现：（1）孪生素数出现的频率（即行距）逐渐变大；（2）半数偏差为1的即为孪生素数；（3）孪生素数都分布在第2列；（4）孪生素数出现后必换行（因为素数乘以2为偶数，这是分组的条件，所以自然必须换行）；（5）每一行的列数可以有很多但不是无穷的（因为素数的个数是无限的，就是说表中有无限行，也就是说每一行的列数可以很多很多，但不能是无穷多，如果存在一行有无穷多就无法换行了，及行数有限，这与素数无穷多矛盾）；（6）除了第一个素数2所在的列，其它所有行都至少有第2列（如果某一行没有第2列，则下一行首位素数与本行首位素数间的整数不能用两个素数之和表示，这与哥德巴赫定理矛盾-由于除了2任意两个素数加和是不等的，且都是偶数。所以当第x个素数N前的素数可以表示N内所有偶数时，第x+1个素数到第x个素数间的偶数必能被全部素数两两加和表示，不然第x个素数之前存在不能被全部表示的区间，一直往下推，可推出31以内、5以内素数不能全部表示其内部的偶数，这与事实矛盾。所以任何素数区间内的偶数可由区间内的素数两两加和表示，及哥德巴赫猜想得证）；由此可证明孪生素数猜想可以依据表而转化为证明“除了第一个整数所在的行，其它行必须有第2列，且有无穷多个整数在第2列换行”。

前一半很容易证明，因为只有2和3两个素数的距离为1，所以其它任一整数必须存在第二列；但无穷多如何证明呢？这需要借用素数的无规性。

素数的无穷多已被欧几里得证明，但素数的无规性如何证明呢？因为素数出现的条件只随素数自身改变，所以其天生具有不确定性，即无规性。因为素数的无规性，所以对于任一>4的整数X，必存在N（N

2.合数的素数因子性质

众所周知，整数可以由素数及素数因子乘积表示。参见表2：

由表2可见，从第一个素数2和最小的因子乘积开始，易得合数2=4，且这是唯一表述方法（因为2已经大于2），不难发现2到4之间还存在3，且3不能被唯一的素数2整除，所以此时必须要求3为素数（不然将出现不能被素数因子乘积表示的合数），这就是素数出现的规律。2和3最小的乘积为2=6，4到6之间还存在5，5也不能被所有素数因子乘积表示，由此可判定5为素数；再试试2=10，6到10之间存在7、8、9，7不能被所有素数因子乘积表示，由此可判定7为素数，而8=2，9=3，故为合数；注意，此时最小的素数因子乘积为2=12，10到12之间存在11，所以11为新素数；接下来最小的乘积（整数）自然轮到2=14，12到14之间存在13，所以13为素数；如此可以找出所有的素数，且可以轻易发现一个错误和一个规律，即在计算2时漏掉了更小的2和3；由此可知漏掉的8和9是必能被已知所有素数乘积表示的合数，即一个规律为“素数为不能用从最小素数因子逐级乘积表示的非连续整数”。（顺便提一下由于用的是因子的乘积，所以无论已知素数有多少，总不能使整数连续，非连续项即为新素数，即素数有无穷多得证），也正是因为合数的“因子逐级乘积性质”，必有无穷多个素数S，使得S+2也为素数。因为如果在第x个素数Sx后任一Sx+n+2都不是素数，Sx+n+2到2 （Sx+n+2）间将会出现无法被Sx+n前素数以因子乘积形式表示的情况，所以必须有无穷多个连续的奇素数出现，及孪生素数有无穷多个。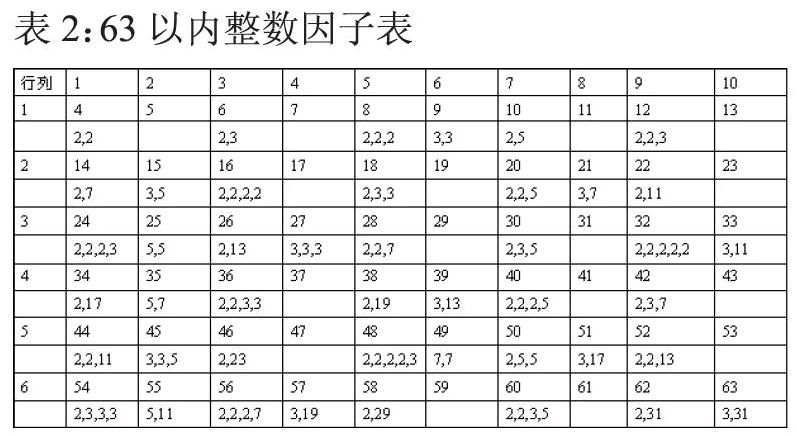

三、素数规律

上述证明的素数无规性是素数基本的规律之一，但其最基本的规律应该是定义，即“正因数只有1和其本身的自然数”。不过这不是我们所要的素数出现规律。关于素数的寻找，最著名的莫过于筛选法，即通过对整数Y逐级开根号和去除根号内素数的倍数来确定Y内的素数。但此法必须是能开根号的数，那么对于不是太大的数能否有一个可以找出任意整数前素数的方法呢？答案当然是有。

1.素数的对称性

整数可表示为“两个素数和的加和”的性质也可以看做是素数的一种对称性质，仔细观察表1即可发现：“从3到任何素数A范围内的素数中必存在至少一个素数与A到2A间的素数关于点A对称。”即通过2A逐一减去A以内的素数即可得到包含A到2A间所有剩余素数的集合，再逐一排除因子为3到A内的素数的数，剩下的即为A到2A内的全部剩余素数。如此从小到大即可找出所有素数。

2.整数的连续性

由此自然可以想到是否可以利用合数的素数因子性质发现分布规律呢？当然可以，这就是整数的连续性。从最小的唯一素数2开始，它作为因子最小可表示4，不连续，那么这个不连续的数必为素数，即有了3；2和3可表示的僅大于4的数为6，也是不连续的，这个缺失项5必为素数；这3个素数因子可表示大于6的最小数为8，缺失的7为素数；至此4个素数因子可表示大于8的最小数为9；连续，所以接下来是这4个素数因子表示大于9的最小数为10；连续，下一个最小数为12，缺失的11必为素数…再用这5个素数乘积逐级表示，凡是遇到不连续的整数就必为素数，如此也可找出所有素数。

以上两种方法均可逐一找出所有素数，若加之超级计算机将如虎添翼。另外如何验证所找出素数的完整性呢？可以将所有素数乘积再加1，如果该数为合数则表示素数间有缺失项。

全文通过一种全新的思路，利用非素数和与非素数因子乘积表示的整数即为素数的两种思路，将整数以双素数和与素数因子乘积的形式分别列入一个分布阵列表中，通过观察发现素数及孪生素数的某些规律，并结合这些规律将孪生素数猜想的形式转变为“除了第一个整数所在的行，其他行必须有第2列，且有无穷多个整数在第2列换行”与“已知小素数乘积不能表示的整数即为素数”两种新形式。再结合素数性质分步证明孪生素数猜想，最后结合该表提出了两种新的寻找已知素数后下一个素数的方法。

参考文献：

[1] Zhang， Yitang.Bounded gaps between primes：Annals of Mathematics （Princeton University and the Institute for Advanced Study），May 21，2013.

（责任编辑 曾 卉）