高弯度曲流河砂体规模定量表征研究
2017-04-14王海峰范廷恩宋来明胡光义梁旭王帅刘向南
王海峰,范廷恩,宋来明,胡光义,梁旭,王帅,刘向南
中海油研究总院,北京 100028
高弯度曲流河砂体规模定量表征研究
王海峰,范廷恩,宋来明,胡光义,梁旭,王帅,刘向南
中海油研究总院,北京 100028
曲流河砂体储层是重要的陆相碎屑岩储层类型,采用“将今论古”的思路,以一系列现代高弯度曲流河的基础数据分级构建定量知识库,实现对地下砂体规模的定量表征。从曲流河成因和形态方面对定量表征开展可行性分析,在相对平坦的地形条件下,当河流通过增加河道弯度和加长流路来减小河道坡降比以趋于输沙平衡且做功最少,同时堤岸主要由细粒物质组成时,河型向曲流河转化,河道平面几何形态呈正弦派生曲线,在演化过程中河道形态和砂体规模保持良好的规律性;结合储层构型理论的分级表征思路,基于砂体规模的不确定性,通过现代沉积数据选取恰当的置信水平,分级构建多组经验公式,形成高弯度曲流河定量知识库;压实减孔量是沉积物埋藏后体积减小的主要因素,通过去压实校正,建立现代沉积与地下砂体的定量联系,对地下曲流河砂体规模进行原始沉积状态下的定量表征。经实际资料验证,结果客观准确。
曲流河;高弯度;定量表征;可行性;不确定性;去压实校正
0 引言
曲流河砂体储层是重要的陆相碎屑岩储层类型,在中国东部中新生代含油气盆地中占有极高的比重[1],具有横向变化快、非均质性强、采收率低等特点。进入油田开发中后期,基于储层构型研究,正确认识曲流河砂体的形态和规模,对于分析储层非均质性和剩余油分布规律等有重要意义。但大部分砂体储层深埋于地下,依靠目前的测井和地震资料难以对其进行直观的表征,尤其是针对单砂体,而采用“将今论古”的方法,利用现代曲流河沉积建立定量知识库,然后将其应用于地下砂体规模的定量预测,不失为一个有效的思路。
研究表明,曲流河的形成和演化遵循一定的动力学和形态规律,国内外对曲流河的几何形态和砂体规模的定量研究给予了高度关注,由现代沉积和野外露头收集数据,总结了丰富的经验公式,并用于指导地下储层研究。Schumm[2]依据弯曲度(k)将北美大平原(Great Plains)上的50个单河道段划分为顺直、过渡、规则弯曲、不规则弯曲、扭曲五种类型,并建立了弯曲度(k)与河道宽深比(F)的定量关系;Leeder[3]在整合前人工作的基础上,指出高弯度曲流河(k>1.7)满岸宽度(w)与满岸深度(h)具有良好的相关性,且点坝厚度大致等于河道满岸深度;随后Lorenzetal.[4]通过对现代曲流河数据的统计分析,提出满岸宽度(w)与曲流带宽度(Wm)的定量关系。此外,还涉及丰富的河道宽深与河道横断面积、河水流量、流速、沉积物粉泥质含量等参数相关关系的研究成果[2,5-8]。
Google公司于2005年推出了以网络为平台的地图服务系统——Google Earth,该软件在地学领域的数据库建立和路径识别上具有较好的实用性,具体到河流研究,Google Earth具有宏观观察河流形态、定量测量河流规模的能力。国内学者基于此做了大量有益的工作,涉及曲流河参数定义及测算[9],国内外典型曲流河河道宽度与点坝跨度的定量关系及其对地下点坝砂体构型分析的指导[10-11],以及曲流河砂体定量知识库的初步构建等[12]。
曲流河的形成和演化受控于物源供给量、地形坡度、水动力条件、基准面旋回变化等多种因素,任何单一因素的改变都会影响其形态和规模,描述砂体规模的两个或多个参数间具有高相关性的同时也存在不确定性,而目前的定量研究成果集中体现在理论值的刻画,忽视了其可能的变化空间;同时,现有定量表征的经验公式多源于对现代曲流河沉积的研究和总结,将其用于地下砂体的定量预测时,往往忽视砂体埋藏过程中的体积变化,或简单采用常数1.1作为压实系数进行厚度校正,导致结果偏差。本文利用可直接观测的现代沉积进行曲流河砂体的定量表征研究,充分考虑其实际可能性,并建立现代沉积物与地下砂体间的定量联系,对地下砂体进行定量预测,其结果可为储层构型研究和地质统计学反演等工作提供定量依据。
1 定量表征的可行性分析
曲流河是自然界中重要的河流类型,其沉积环境、沉积物特征、水动力条件和几何形态等均具有特殊性,有别于辫状河等其他河型,这也正是其定量表征的可行性基础。
1.1 曲流河河型成因
在相对稳定的地形条件下,床沙质来量和河岸抗冲性是决定河型的主要因素[13-14]。相对于辫状河等,曲流河多形成于相对平坦的地形条件。
河流的形成是其自动调整的结果,在河水流量和泥沙含量一定的情况下,河流将调整其坡降比、形态、河床物质组成等,最终调整河型,使得上游的水和泥沙能够通过下游河段下泄,保持相对平衡,并使能量消耗在沿程分布遵循一定的统计规律[13]。
输沙平衡的要求决定河型之间的演变。对于河流的输沙能力,河水含沙量约与流量成正比。假设支流与干流的含沙量基本一致,当支流汇入干流后,则干流的含沙量基本不变,而水量增加。即相对于含沙量,从水量考虑的输沙能力是个调整的主要要素。也就是说,越到下游,随支流汇入和水量增加,含沙量相对水量来说越来越小,河流为趋于平衡,河道坡降比将不断减小,以降低河水流速,进而减小流量。这种坡降比的调整有一部分是通过河道弯曲、加长流路实现的,河型即向曲流河转化[14]。
河流自身调整以趋于输沙平衡为目的,以水流做功最小为约束。水流做功最小指单位重量的水在单位时间内所消耗的能量力求达到当地具体条件(如地形坡度、物源供给、水动力强度等)所允许范围内的最小值[15]。结合曼宁公式,以及流量与河道断面面积的关系,得到
Uj=n-0.6Q0.4j1.3B-0.4=最小
式中,n为曼宁糙率系数,Q为流量,j为水流能坡,可用地形坡度代替,B为河道横断面的水面宽度。其中,Q为外在条件,其余三者则为河流能够调整的自由变化因素,可通过三种方式或其组合来满足水流做功最小,即:加大河床和堤岸阻力,减小河道坡降比以及增加河宽。若最终调整的结果是以增加河道长度、减小河道坡降比为主,则河流发展为曲流河[13]。
此外,堤岸的抗侵蚀能力是决定河型形成的另一重要因素。尤联元等[16]曾统计了国内多条河流的河岸情况及其他因素对河型的影响,将河岸与河床的相对可动性定量为河床床砂粒度中值与河岸中粉泥质含量的相对关系,认为河岸为二元结构,粉泥质厚度大于砂砾质,粉泥质含量大的情况下,易形成曲流河。
输沙平衡、能量分配和河岸物质组成等影响河型的因素分析表明,在相对平坦的地形条件下,河流通过河道弯度和加长流路来实现河道坡降比减小,以趋于输沙平衡且做功最少,同时河岸主要由细粒物质组成,河型向曲流河转化且弯曲度不断增大。
1.2 曲流河平面几何形态
在成因条件约束下,曲流河的平面几何形态也具有独特性,河道由一系列河弯(即曲流段,也称蛇曲段)和与之相连的直段组成。
河流以坡降比形成的重力势能提供动力条件,从上游向下游搬运泥沙沉积物。沿河谷方向的两点之间,在保持相同坡降比时,河水可流经不同的流路,在所有可能的流路中间,必然有一条具有最大的可能性,且在该流路上河水做功最小。Langbeinetal.[17]研究认为,这条最可能出现的流路可以通过随机游移的模式确定,该模式决定了曲流河河道的几何形态。
假设河流沿流路前进Δx,相应地河道偏离原来方向的角度为Δφ(图1A),Δφ出现概率为p,同时假设该偏离角度具有正态分布,即该随机游移模式可确定多种不同的流路,其中出现概率最大的流路相当于:
满足上述条件的角度应是沿着流路的距离的正弦函数,即,
其中,φ为距离x处的方向角,L为河弯长度,Ω为流路与河谷方向所成的最大夹角(图1B)。图1C为Ω=40°、90°和110°时的流路,其本身不是正弦曲线,而是由正弦函数派生出来的曲线,将其称为正弦派生曲线,即在理想模式下或者受外界影响较小时,河道的平面形态呈正弦派生曲线。在此基础上,加入河道发展稳定性以及河道变化扰动周期分析,以模拟天然曲流河,其结果与实际河流具有良好的相似性[18-19]。
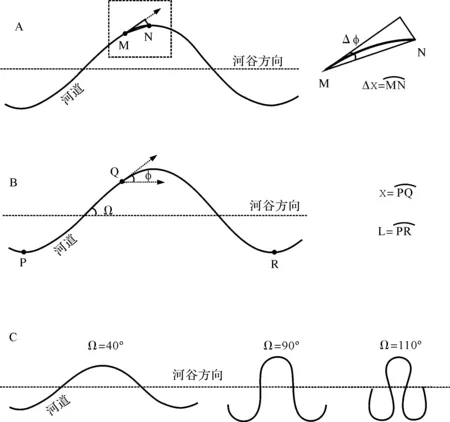
图1 曲流河河道平面几何形态(图C据文献[13])A,B.曲流河流路游移模式;C.不同夹角的曲流河流路Fig.1 Plane geometrical morphology of meandering river channel (Fig. C from reference[13])
曲流河的演化是一个蚀凹增凸、河道逐渐废弃的过程,其河道形态也随之演变。在洪水期的曲流段内,由于河道断面凹岸陡凸岸缓的不对称性以及科里奥利力的作用,河道内水流形成不对称流速场,即横向环流与沿程纵向水流构成的螺旋流,控制着河道迁移与点坝形成,成为曲流河侧向侵蚀与点坝沉积的根本原因[20]。
曲流河的螺旋流将凹岸侵蚀形成的沉积物不断搬运到凸岸堆积,蚀凹与增凸在数量上近似相等,故河道在河谷内做迁移摆动,其横断面几何形态变化不大(图2),因此曲流河河道在演化过程中保持良好的规律性。以加拿大比顿河为例,河道开始由直变弯时,曲率半径较大,在河道发展过程中曲率半径与河宽的比值就不断降低至最低值(约2.08),此后一直在该值附近变化(均值约2.19),该河流其他10个河段的演化也表明,曲率半径与河宽的比值最终稳定在2~3[21]。

图2 曲流河侧迁过程中的河道变化(下荆江来家铺,据[13])A.河道侧迁位移和断面形态;B.河岸垮塌与沉积累积曲线Fig.2 The channel variation during the lateral migration of meandering river (Laijiapu of lower Jingjiang river, from reference[13] )
实际河弯的平面几何形态可简化为对称的圆弧形,随河弯的发展,其形态随之发生改变,但基本都是正弦曲线的演变,单个河曲段仍是近似对称圆弧形,可归纳为以下几类:延伸、平移、旋转、扩大、侧向移动和复杂变化(图3)。河弯的发展过程是渐进的,当河道弯曲度较小时,发展较快,随弯曲度变大,河道接近河道带的边缘,河弯发展速度逐渐减慢,当河弯发展到极限时,则形成截弯取直,即形成废弃河道。
分析表明,曲流河的形成和演变是一个受动力学和形态因素控制的过程,具有较强的规律性,对其砂体规模的定量分析具有可行性。

图3 曲流河河道变化类型(据文献[22],有修改)Fig.3 Change type of meandering river channel (modified from reference[22])
2 高弯度曲流河定量知识库构建
在可行性分析的基础上,结合河流相储层构型理论的分级表征思路,实测和调研了大量典型的高弯度曲流河,如国外的亚马逊河、密西西比河、马兰比季河以及国内的荆江、松花江、拉林河、伊敏河、海拉尔河、额尔古纳河、嫩江等,厘定不同级次砂体规模的参数,选取合适的置信水平(confidence level),构建经验公式对参数间的相关性和不确定性进行描述。
2.1 定量表征参数
油田开发进入中后期,储层构型成为重要的研究内容。曲流河砂体储层构型研究具有层次性,包括复合曲流带、单一曲流带、点坝、侧积体等级次。其中复合曲流带规模较大,大于地震分辨率,以井震结合的方式可对其进行有效表征,本文主要定量分析单一曲流带、活动河道、点坝和侧积单元等级次的参数,涉及曲流带宽度Wm、河道满岸宽度w、河道满岸深度h、河弯曲率半径Rc、点坝跨度(或称长度)Lp、侧积层水平宽度wL、侧积层倾角β以及河道弯曲度k(图4)等,数据来源于Google Earth软件实测和已发表成果。
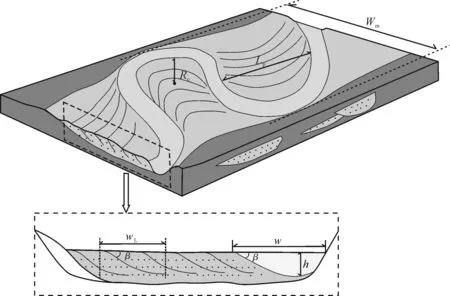
图4 曲流河砂体形态及相关参数Fig.4 Sandbody morphology and relevant parameter of meandering river
河道弯曲度k指河道长度与河谷长度的比值,是定义河流类型的重要参数之一,曲流河以单河道和k>1.5(也有人定为1.3)为特征。前人在实际测量中多利用某点坝弧长与点坝跨度的比值作为该段河道的弯曲度k[12],但是高弯度曲流河形态复杂,往往出现单个点坝内发育大量侧积体,点坝跨度(平行于河谷方向)远小于点坝宽度(垂直于河谷方向)的情况,或者出现在较短的河谷距离内多个曲流段嵌套的情况,该方法计算的k值偏小;而对于低弯度曲流河,相邻点坝间可能发育平行于河谷方向的较长直段河道,该方法计算的k值偏大。鉴于此,本次实测数据取至少包含3个相邻曲流段的河道长度与该段河谷的比值为弯曲度k,该方法更符合统计学意义。
在相对稳定的沉积背景下,曲流河河道不断侧向迁移,伴随弯曲度k变大,点坝砂体逐渐形成,河道最终废弃。Schumm[2]通过研究一系列混合负载型河流(即相当于曲流河)的弯曲度,发现k=1.7是这些河流弯曲度的中值。根据研究经验,以k=1.7为高弯度(k>1.7)与低弯度(k:1.5~1.7)曲流河的界限[3-4]。高弯度曲流河道侧向迁移能力强,沉积物侧向加积,粒度较细,多为砂泥质;而低弯度曲流河道侧向迁移弱,除侧向加积外,伴有顺流前积,水动力较强,沉积物粒度较粗,含砂砾质。随地形高差、河流演化阶段等变化,高、低弯度曲流河可相互转化。
研究表明,高弯度曲流河的宽度、深度、点坝跨度等参数间具有良好的相关性[3,11],且曲流河河道废弃后点坝砂体逐渐沉积于地下,形成油气储层,最终呈现的也多是高弯度形态,因此本文以高弯度曲流河为研究对象。
2.2 基于不确定性分析的经验公式构建
可行性分析表明,曲流河在形成和演化过程中,其几何形态和砂体规模保持良好的规律,高弯度曲流河参数之间具有高相关性。同时需要注意到,实际河流在形成过程中,除受到地形坡度、沉积物供给量、水动力条件、沉积旋回变化等因素影响外,还受气温、降水量、植被发育情况等多种地理条件制约,其中任何一个影响因素或外界条件的变化均可导致曲流河砂体规模的变化,其参数间具有高相关性的同时也存在一定的不确定性。此外,不确定性还源于以下两个方面:1)砂体测量中产生的误差,2)对于调研的数据,不同的学者对某参数的理解可能存在细微差异,从而导致数据结果的误差。
基于统计学置信水平的分析,本文根据大量实测和调研数据,采用最小二乘法拟合经验公式描述参数间的相关性,同时选取相对较低的75%置信水平拟合经验公式,获得可信度较高的砂体规模变化空间(即置信区间),以描述其不确定性。
2.2.1 单一曲流带
曲流河蚀凹增凸,河流演化的结果是河道侧向迁移,凸岸位置形成点坝,沿河谷方向,一系列点坝构成曲流砂带。
曲流带宽度Wm受河道规模和河道弯曲度k等影响,在k>1.7的情况下,曲流带宽度Wm与河道满岸宽度w呈现正相关关系,图5是全球多条k=1.7-2.7的曲流河Wm与w散点图,利用最小二乘法拟合两参数间的经验公式为:
Wm=7.00w1.06(R2=0.90)
同时考虑到砂体规模的不确定性,选取75%的置信水平,确定Wm相对于w的上限A与下限B:
A:Wm=8.69w1.11
B:Wm=5.64w1.01
以河道满岸宽度w=100 m为例,相应曲流带宽度Wm的理论值约920 m,其上限约1 440 m,下限约590 m。

图5 单一曲流带宽度Wm与河道满岸宽度w的相关性(部分数据据文献[6-8])Fig.5 The correlation between single meander belt width and bankfull width (partial data from references[6-8])
此前Lorenzetal.[4]也曾开展类似工作,得到曲流带宽度Wm与河道满岸宽度w的相关关系
Wm=7.44w1.01(R2=0.93)
随后该式得到广泛应用。显然,就绝大多数曲流河而言,以Lorenz的公式计算得到的曲流带宽度要小于本文理论值经验公式的结果,原因在于Lorenz用于拟合的部分数据收集于低弯度曲流河(k<1.7),其曲流带宽度略小[4]。
2.2.2 活动河道
活动河道涉及参数主要是河道满岸宽度w和满岸深度h。满岸宽度与深度广义上指洪水退去之前的河道宽度与深度的最大值,会随洪水过程的复杂程度而改变。在现代曲流河研究中,普遍认为满岸宽度是指点坝顶部到侵蚀岸的水平距离,满岸深度的测量方向与满岸宽度垂直,在河道深泓线(即沿河流方向最大水深处的连线)上,一般认为砂质沉积物的厚度(即点坝厚度)近似为满岸深度。
Leederetal.[3]收集和测量了104组现代河流的满岸宽度与深度数据,河流弯曲度k=1.0-2.5,即从顺直河到高弯度曲流河,整体而言两者相关性较差;而对于高弯度曲流河(k>1.7)而言,两者相关性较好。本次研究选取Leeder公式的57组原始数据(k>1.7),以最小二乘法拟合得到满岸宽度w与满岸深度h间的相关关系(图6):
w=8.94h1.40(R2=0.83)
同样选取75%的置信水平,确定w相对于h的上限A与下限B:
A:w=10.96h1.49
B:w=7.25h1.30

图6 满岸宽度w与满岸深度h的相关性(部分数据据文献[7,23-25])Fig.6 The correlation between bankfull width and bankfull depth (partial data from references[7, 23-25])
以满岸深度h=5 m为例,相应满岸深度w的理论值约为85 m,其上限约为120 m,下限约为60 m。
由于基于相同的基础数据,本次建立的理论值经验公式与Leeder公式w=6.8h1.54计算结果基本一致,公式表达形式略有差异。
2.2.3 点坝
受河流侵蚀下切的影响,点坝的空间形态以顶平底凸为特征,平面形态受河弯限制,在靠近凹岸处点坝呈圆弧形,在河流演化的最终阶段具有相对固定的原点和曲率半径Rc,同时点坝的跨度(或称长度)Lp受河弯起点与末端的两个直段河道控制,Rc与Lp均可度量。
典型高弯度曲流河的满岸宽度w与河弯曲率半径Rc的散点图(图7)显示,两个参数间具有良好的相关性,利用最小二乘法拟合其经验公式:
Rc=2.11w1.04(R2=0.92)
以75%的置信水平,确定Rc相对于w的上限A和下限B:
A:Rc=2.57w1.09
B:Rc=1.73w

图7 河弯曲率半径Rc与满岸宽度w的相关性(部分数据据文献[6-7,23,25])Fig.7 The correlation between curvature radius of river bend and bankfull width (partial data from references[6-7, 23, 25])
以满岸宽度w=100 m为例,相应河弯曲率半径Rc的理论值约为250 m,其上限约为390 m,下限约为170 m。
典型高弯度曲流河河道满岸宽度w与点坝跨度Lp的散点图(图8)显示,两者间也具有良好的相关性,利用最小二乘法拟合其经验公式:
Lp=7.02w0.92(R2=0.90)
以75%的置信水平,确定Lp相对于w的上限A和下限B:
A:Lp=8.13w0.95
B:Lp=6.06w0.89

图8 点坝跨度Lp与满岸宽度w的相关性(部分数据据文献[10-12,26])Fig.8 The correlation between length of point bar and bankfull width (partial data from references[10-12, 26])
以满岸宽度w=100 m为例,其点坝跨度Lp的理论值约为485 m,其上限约为645 m,下限约为365 m。
2.2.4 侧积单元
随储层构型理论的提出和应用,以及油田开发后期对剩余油研究的深入,点坝内部的非均质性逐渐引起人们的重视。点坝内存在多种成因的夹层,以洪水后河道内悬浮沉积的泥质侧积层为主。侧积层的形成与单次洪水事件有关,每一次洪水造成曲流河凹岸侵蚀、凸岸沉积,洪水末期能量衰减,洪水携带的细粒泥质在点坝砂体上披覆沉积,形成薄层的泥质沉积物,即侧积层,侧积层之间的砂体单元称侧积体,显然侧积层是点坝内部重要的构成单元。
相对于曲流带和点坝级次,侧积体规模要小得多,且易被后期洪水破坏,其数据的采集存在较大困难,如Allun[27]在采集的231个泥盆纪样品数据中,只有11个相关数据。数据的稀缺和测量的困难,导致对于侧积体规模的研究较薄弱。
目前普遍认为,侧积层在水平面的投影宽度wL大致等于河道满岸宽度w的2/3[28],即:
wL=2/3w
侧积层的倾向可通过点坝的侧积过程以及废弃河道的位置确定,侧积层总是向废弃河道方向倾斜,其倾角β大致与河道横断面中河床与水平面的夹角相等:
以上即为高弯度曲流河不同级次的砂体规模参数间的相关性及不确定性,据此构建定量知识库(表1)。

表1 高弯度曲流河砂体规模定量知识库
3 地下砂体规模定量表征方法
高弯度曲流河砂体规模定量知识库源于对现代沉积的研究,将今论古,可将其用于对地下曲流河砂体规模的定量认识。
3.1 砂体体积变化分析
松散沉积物沉积于地表后逐渐被埋藏,由于温度、压力和流体等因素影响,经历成岩作用形成坚硬的岩石,随埋藏时间增长和深度增加,沉积物(岩)体积逐渐减小。因此将现代沉积的结果用于地下砂岩研究,应首先还原地下砂岩的原始地表沉积状态,恢复其沉积时的体积,建立现代沉积与地下砂岩的定量联系,以获得合理的表征结果。
砂岩的体积减小包括孔隙减小和颗粒骨架压缩两部分,但颗粒骨架的压缩相对于孔隙体积的变化而言十分有限,即孔隙度变化是砂岩体积减小的主要影响因素[29]。
研究表明,压实作用是碎屑岩孔隙减小的主要成岩作用类型[29-31],压实作用过程中由于上覆地层、水层的重荷或构造应力作用,沉积物(岩)发生水分排出、孔隙度降低、体积缩小,在沉积物埋藏的早期阶段压实作用表现得尤为明显。以中国北方主要含油气盆地为例,砂岩的压实减孔量平均为11.1%~25.3%,占总减孔量的50.0%~94.0%,大致是其他成岩作用减孔量的2~10倍[29]。因此,可通过去压实校正,近似恢复地下砂体沉积时的原始体积。
假设沉积物(岩)埋藏过程中平面面积基本保持不变,只有垂向厚度发生变化,则可通过计算机械压实作用下的孔隙度减小,校正埋藏成岩过程中砂质沉积物的体积变化,即砂岩的去压实校正。
Magara[32]对页岩孔隙度变化与其埋深关系做了详细研究,并做出定量描述:
φ=φ0e-cz
式中,φ0、φ分别为地表和埋深z时的页岩孔隙度,c为压实系数(单位m-1)。后来Hegartyetal.[33]将该公式的应用范围推广到各种碎屑岩,如泥岩、砂岩等,并得到不同岩石类型的压实系数c。
根据骨架颗粒体积不变、孔隙度减小的假设,确定沉积岩(物)在埋深过程中厚度变化的定量分析:
式中,φ0为沉积物在地表沉积时的初始孔隙度,c为压实系数,H0为地表沉积时的沉积物初始厚度,z为埋藏深度,H为与埋深z对应的岩石厚度[34]。
设定砂岩(含粉砂岩、砂岩、砂砾岩等)初始沉积时孔隙度φ0=45%,压实系数c=0.000 25,计算得到了不同原始厚度(20 m,30 m,40 m,…,90 m,即沉积于地表时厚度)的砂质沉积物在不同埋深处的厚度变化(图9)。
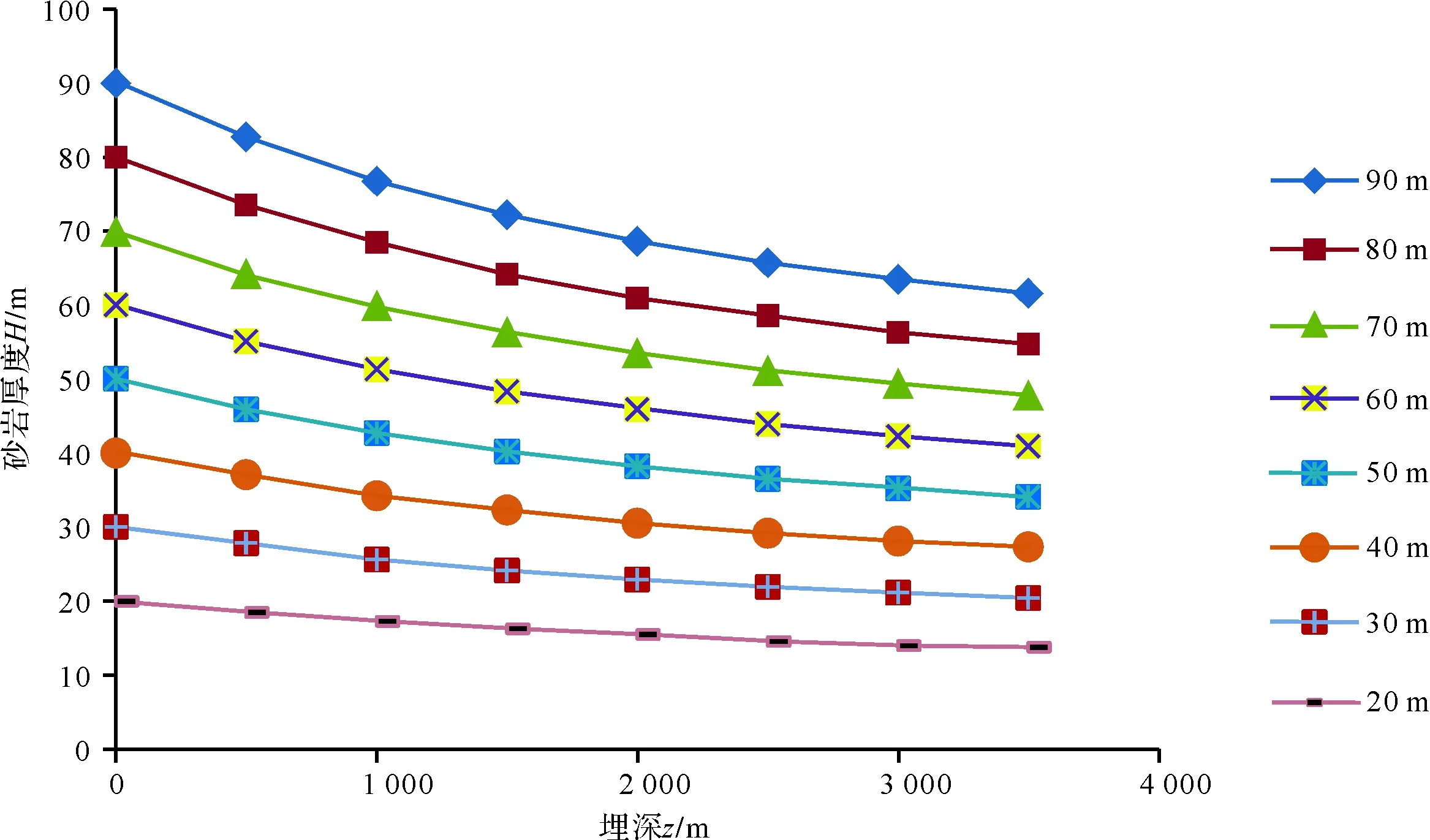
图9 砂岩在埋藏过程中的厚度变化(数据据文献[34])Fig.9 Thickness variation of sandstone in the process of burial (data from reference[34])
将上述H0与H之比定义为压实率n,即n=H0/H。分析表明,砂岩压实程度与其埋藏深度有关,而与其厚度无关,且表现出浅层压实快、深层压实慢的特点(表2)。因此,可拟合得到压实率n与埋深z的关系(图10):
n=-2×10-8z2+2×10-4z+0.9996 (R2=
0.99)
该公式的数据点源于理论推导,而非实际测量,因此两者相关系数接近1。
表2 不同埋深下的砂岩压实率
Table 2 Sandstone compaction rate in different burial depth

埋深z/m0500100015002000250030003500压实率n11.091.171.251.311.371.421.46

图10 不同埋深下的砂岩压实率Fig.10 Sandstone compaction rate in different burial depth
据此可近似建立现代砂质沉积物与地下砂体间的定量联系,恢复地下某深度处砂岩的原始沉积厚度。以地下2 000 m深度处的5 m厚砂岩为例,其沉积时的原始厚度约为6.55 m。
3.2 地下砂体规模定量表征
在建立高弯度曲流河砂体规模定量知识库以及砂岩去压实校正的基础上,可对地下曲流河砂体规模形成定量认识。
3.2.1 定量表征方法
利用测井资料对岩性的解释成果,得到地下单一完整点坝砂岩厚度H,经去压实校正恢复点坝沉积时的原始厚度H0,将其视为河道满岸深度h,利用经验公式求得相应满岸宽度w,进而利用相关经验公式获得不同级次单元的规模。即,可直接建立地下某深度z处点坝砂体厚度H与相应河道满岸宽度w、曲流带宽度Wm、点坝跨度Lp、曲率半径Rc、侧积层水平宽度wL等参数间的定量关系,实现对地下曲流河砂体规模的定量表征(图11)。
在计算某参数的上(下)限时,采用两个经验公式上(下)限的叠合,如获取河流满岸深度h后,用上限经验公式w=10.96h1.49计算得到相应满岸宽度的上限,再经上限经验公式Lp=8.13w0.95计算得到点坝跨度的上限。
需要注意的是,依据垂向韵律、测井曲线形态等准确确定单井上的单一完整点坝砂体是后续表征的基础,应排除多期点坝叠置砂体、河道间砂体、点坝砂体边部等情形。
3.2.2 合理性检验
基于定量知识库和去压实校正的高弯度曲流河砂体规模定量表征方法,可经实际开发油田资料验证其合理性。
大庆油田的萨尔图、葡萄花油层和胜利油田的馆陶组油层都是典型的高弯度曲流河储层,开发历史长,井网密度大,对地下砂体的形态和规模认识清晰。以此为例(表3),松辽盆地大庆杏南油田PI31b单元,埋深1 100 m,地下点坝厚度6.0 m,经去压实校正后,利用本次拟合的经验公式计算得到废弃河道宽度(即满岸宽度)理论值w=140 m(下限94 m,上限205 m),实际值120 m;计算得到曲流带宽度理论值Wm=1 350 m(下限550 m,上限3 250 m),实际值约1 500 m。胜利油田孤东七区中单元Ng5(2)小层,埋深1 300 m,地下点坝厚度约6.0 m,经去压实校正后,利用本次拟合的经验公式计算得到曲流带宽度理论值Wm=1 360 m(下限570 m,上限3 220 m),实际值1 100~1 400 m。对比显示,理论值与实际值接近,且实际值落在下限与上限之间。此外,大庆油田萨北、加拿大Fort McMurray等地区的资料也表明,本次建立的定量表征方法合理、可行。

图11 高弯度曲流河砂体规模定量表征流程Fig.11 Quantitative characterization flow chart of sand body scale in high sinuosity meandering river
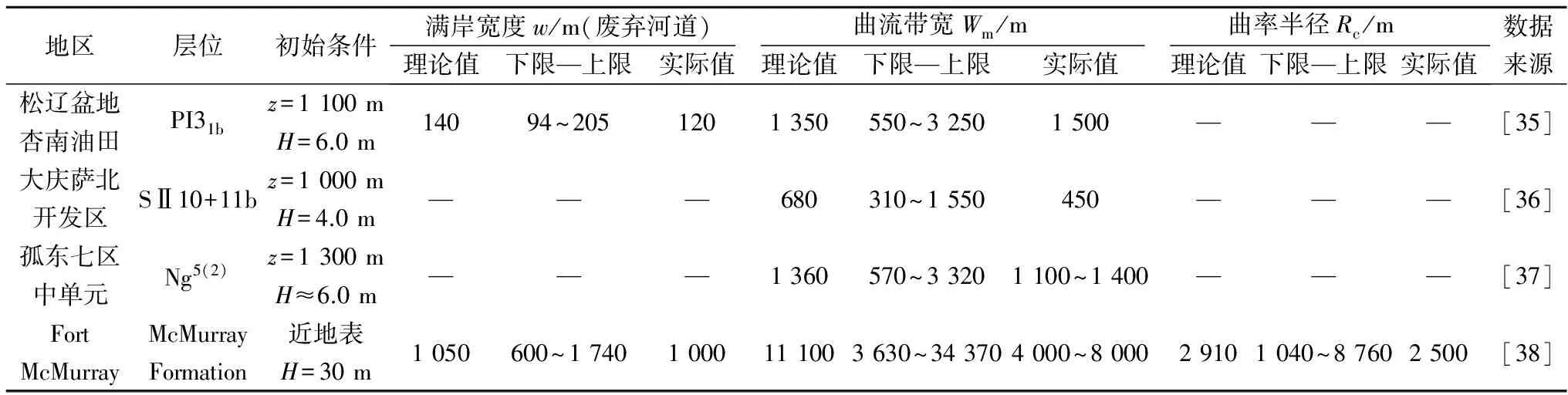
地区层位初始条件满岸宽度w/m(废弃河道)曲流带宽Wm/m曲率半径Rc/m理论值下限—上限实际值理论值下限—上限实际值理论值下限—上限实际值数据来源松辽盆地杏南油田PI31bz=1100mH=6.0m14094~2051201350550~32501500———[35]大庆萨北开发区SⅡ10+11bz=1000mH=4.0m———680310~1550450———[36]孤东七区中单元Ng5(2)z=1300mH≈6.0m———1360570~33201100~1400———[37]FortMcMurrayMcMurrayFormation近地表H=30m1050600~17401000111003630~343704000~800029101040~87602500[38]
目前,储层构型是油田开发的重要研究内容,与此对应,本次建立一套不同级次的曲流河砂体规模定量表征思路,以单一点坝砂体厚度为基础,可直接对曲流带、点坝、侧积单元等级次的砂体或界面规模形成定量认识,方法简单实用;结合砂体去压实校正,在计算砂体规模理论值的同时,计算实际砂体规模的上限和下限,使不确定性得到充分体现,结果客观合理。以此为基础,对砂体规模的定量认识可为储层构型研究、地质统计学反演等工作提供定量依据。
4 结论与讨论
河流的输沙能力、能量分配和堤岸物质组成等是决定河型的重要因素,当河流通过增加河道弯度和加长流路来减小坡降比,且堤岸主要由细粒物质组成时,形成曲流河。曲流河河道呈正弦派生曲线形态,在演化过程中河道形态和砂体规模具有较强的规律性,定量表征具有可行性基础。
结合储层构型理论的分级表征思路,厘定描述曲流河不同级次砂体规模的参数,建立参数间的相关性,同时选取合适的置信水平,表征砂体规模的不确定性,形成高弯度曲流河定量知识库。压实减孔量是沉积物埋藏后体积减小的主要因素,通过砂岩去压实校正,建立现代沉积与地下砂体间的定量联系,进而将定量表征方法应用于地下砂体储层。经实际资料验证,结果客观准确。
需要注意到,任何方法都有其应用局限性。受限于河道深度不便于直接测量等原因,难以直接建立河道深度与砂体规模的定量关系,本次研究以河道宽度为过渡,首先建立河道宽深关系以及河道宽度与砂体规模的关系,进而以河道深度推导砂体规模,不确定性的叠加,致使最终砂体规模不确定性的范围较大,因此地质知识库的建立尚有补充空间,例如通过收集数据直接建立河道深度与砂体规模的定量联系,或者是增加沉积物粒度分布、河道弯曲度、地形破降比等参数约束,以减小砂体规模的不确定性。同时,除压实作用外,其他成岩作用类型对砂岩体积变化也有少量影响,可采用加权平均的方式,定量完善地下砂岩体积校正。
References)
[1] 薛培华. 河流点坝相储层模式概论[M]. 北京:石油工业出版社,1991:1-20. [Xue Peihua. An Introduction to Reservoir Models of Point Bar[M]. Beijing: Petroleum Industry Press, 1991: 1-20.]
[2] Schumm S A. Sinuosity of alluvial rivers on the Great Plains[J]. Geological Society of America Bulletin, 1963, 74(9): 1089-1100.
[3] Leeder M R. Fluviatile fining-upwards cycles and the magnitude of palaeochannels[J]. Geological Magazine, 1973, 110(3): 265-276.
[4] Lorenz J C, Clark J A, Heinze D M, et al. Determination of widths of meander-belt sandstone reservoirs from vertical downhole data, Mesaverde Group, Piceance Creek Basin, Colorado[J]. AAPG Bulletin, 1985, 69(5): 710-721.
[5] Williams G P. Paleohydrological methods and some examples from Swedish fluvial environments Ⅱ. River meanders[J]. Geografiska Annaler Series A, Physical Geography, 1984, 66(1/2): 89-102.
[6] Williams G P. River meanders and channel size[J]. Journal of Hydrology, 1986, 88(1/2): 147-164.
[7] Leopold L B, Wolman M G. River meanders[J]. Geological Society of America Bulletin, 1960, 71(6): 769-793.
[8] Carlston C W. The relation of free meander geometry to stream discharge and its geomorphic implications[J]. American Journal of Science, 1965, 263(10): 864-885.
[9] 张斌,艾南山,黄正文,等. 中国嘉陵江河曲的形态与成因[J]. 科学通报,2007,52(22):2671-2682. [Zhang Bin, Ai Nanshan, Huang Zhengwen, et al. Meanders of the Jialing River in China: morphology and formation[J]. Chinese Science Bulletin, 2007, 52(22): 2671-2682.]
[10] 岳大力,吴胜和,刘建民. 曲流河点坝地下储层构型精细解剖方法[J]. 石油学报,2007,28(4):99-103. [Yue Dali, Wu Shenghe, Liu Jianmin. An accurate method for anatomizing architecture of subsurface reservoir in point bar of meandering river[J]. Acta Petrolei Sinica, 2007, 28(4): 99-103.]
[11] 李宇鹏,吴胜和,岳大力. 现代曲流河道宽度与点坝长度的定量关系[J]. 大庆石油地质与开发,2008,27(6):19-22. [Li Yupeng, Wu Shenghe, Yue Dali. Quantitative relation of the channel width and point-bar length of modern meandering river[J]. Petroleum Geology & Oilfield Development in Daqing, 2008, 27(6): 19-22.]
[12] 石书缘,胡素云,冯文杰,等. 基于Google Earth软件建立曲流河地质知识库[J]. 沉积学报,2012,30(5):869-878. [Shi Shuyuan, Hu Suyun, Feng Wenjie, et al. Building geological knowledge database of meandering river based on Google Earth software[J]. Acta Sedimentologica Sinica, 2012, 30(5): 869-878.]
[13] 钱宁,张仁,周志德. 河床演变学[M]. 北京:科学出版社,1987:1-415. [Qian Ning, Zhang Ren, Zhou Dezhi. Fluvial Processes[M]. Beijing: Science Press, 1987: 1-415.]
[14] 钱宁. 关于河流分类及成因问题的讨论[J]. 地理学报,1985,40(1):1-10. [Qian Ning. On the classification and causes of formation of different channel patterns[J]. Acta Geographica Sinica, 1985, 40(1): 1-10.]
[15] Yang C T. Potential energy and stream morphology[J]. Water Resources Research, 1971, 7(2): 311-322.
[16] 尤联元,洪笑天,陈志清. 影响河型发育几个主要因素的初步探讨[C]//第二届河流泥沙国际学术讨论会论文集. 北京:水利水电出版社,1983:662-672. [You Lianyuan, Hong Xiaotian, Chen Zhiqing. A preliminary research on impact of some factors on the developing river patterns[C]//Paper Compilation on the Second International Academic Symposium on River Sediment. Beijing: Water Conservancy and Electric Power Press, 1983: 662-672.]
[17] Langbein W B, Leopold L B. River meanders-theory of minimum variance[R]. United States Geological Survey Professional Paper 422-H. Washington, DC: United States Government Printing Office, 1996.
[18] Parker G, Diplas P, Akiyama J. Meander bends of high amplitude[J]. Journal of Hydraulic Engineering, 1983, 109(10): 1323-1337.
[19] Ferguson R I. Disturbed periodic model for river meanders[J]. Earth Surface Processes, 1976, 1(4): 337-347.
[20] 姜在兴. 沉积学[M]. 北京:石油工业出版社,2003:283-300. [Jiang Zaixing. Sedimentology[M]. Beijing: Petroleum Industry Press, 2003: 283-300.]
[21] Hickin E J. The development of meanders in natural river-channels[J]. American Journal of Science, 1974, 274(4): 414-442.
[22] Hooke J M. The distribution and nature of changes in river channel patterns[C]//Gregory K J. Channel Changes. Chichester: John Wiley, 1977: 265-280.
[23] Schumm S A. River adjustment to altered hydrologic regimen-Murrumbidgee River and paleochannels, Australia[R]. Geological Survey Professional Papers 598, 1968: 65.
[24] Fish H N. Geological investigation of the alluvial valley of the Lower Mississippi River[R]. Vicksburg: Mississippi River Commission, 1944: 78.
[25] Fish H N. Fine grained alluvial deposits and their effects on Mississippi River activity[R]. Vicksburg: Mississippi River Commission, 1947: 82.
[26] 唐金荣,何宇航. 河流相储层单砂体识别与应用[J]. 大庆石油地质与开发,2012,31(3):68-72. [Tang Jinrong, He Yuhang. Recognition of the individual sand body in fluvial facies reservoirs and its application[J]. Petroleum Geology & Oilfield Development in Daqing, 2012, 31(3): 68-72.]
[27] Allen J R L. Studies in fluviatile sedimentation: a comparison of fining-upwards cyclothems, with special reference to coarse-member composition and interpretation[J]. Journal of Sedimentary Research, 1970, 40(1): 298-323.
[28] Allen J R L. The sedimentation and palaeogeography of the old red sandstone of Anglesey, North Wales[J]. Proceedings of the Yorkshire Geological Society, 1965, 35(2): 139-185.
[29] 寿建峰. 中国北方油气盆地砂岩成岩压实作用的动力成因机制与模式[D]. 北京:中国石油勘探开发研究院,2004:1-118. [Shou Jianfeng. Dynamic diagenesis mechanism and mode of sandstone compaction in oil-bearing basins of North China[D]. Beijing: PetroChina Exploration and Development Research Institute, 2004: 1-118.]
[30] 李绍虎,吴冲龙,吴景富,等. 一种新的压实校正法[J]. 石油实验地质,2000,22(2):110-114. [Li Shaohu, Wu Chonglong, Wu Jingfu, et al. A new method for compaction correction[J]. Experimental Petroleum Geology, 2000, 22(2): 110-114.]
[31] 漆家福,杨桥. 关于碎屑岩层的去压实校正方法的讨论——兼讨论李绍虎等提出的压实校正法[J]. 石油实验地质,2001,23(3):351-356. [Qi Jiafu, Yang Qiao. A discussion about the method of decompaction correction[J]. Petroleum Geology & Experiment, 2001, 23(3): 351-356.]
[32] 真柄钦茨. 压实与流体运移[M]. 陈荷立,译. 北京:石油工业出版社,1981:8-9. [Magara K. Compaction and Fluid Migration[M]. Chen Heli, Trans. Beijing: Petroleum Industry Press, 1981: 8-9.]
[33] Hegarty K A, Weissel J K, Mutter J C. Subsidence history of Australia’s southern margin: constraints on basin models[J]. AAPG Bulletin, 1988, 72(5): 615-633.
[34] 方康祖,陈章明,庞雄奇,等. 地史过程中地层砂泥含量的变化及其恢复计算[J]. 大庆石油学院学报,1993,17(增刊1):11-17. [Fang Kangzu, Chen Zhangming, Pang Xiongqi, et al. The changes of strata sandstone percents during burial and their calculation[J]. Journal of Daqing Petroleum Institute, 1993, 17(Suppl.1): 11-17.]
[35] 马世忠,孙雨,范广娟,等. 地下曲流河道单砂体内部薄夹层建筑结构研究方法[J]. 沉积学报,2008,26(4):632-639. [Ma Shizhong, Sun Yu, Fan Guangjuan, et al. The method for studying thin interbed architecture of burial meandering channel sandbody[J]. Acta Sedimentologica Sinica, 2008, 26(4): 632-639.]
[36] 焦艳丽. 大庆油田萨北开发区二类油层储层沉积模式[J]. 大庆石油学院学报,2010,34(3):19-22. [Jiao Yanli. Depositional pattern of the classⅡoil reservoir in the north of Sa'ertu development area of Daqing oil field[J]. Journal of Daqing Petroleum Institute, 2010, 34(3): 19-22.]
[37] 周伟东,刘振坤,岳大力,等. 济阳坳陷孤东油田七区中单元新近系馆陶组点坝构型[J]. 石油与天然气地质,2010,31(1):126-134. [Zhou Weidong, Liu Zhenkun, Yue Dali, et al. An analysis of point bar configuration of the Neogene Guantao Formation in the middle unit of Block 7 in Gudong oilfield, the Jiyang depression[J]. Oil & Gas Geology, 2010, 31(1): 126-134.]
[38] Musial G, Reynaud J Y, Gingras M K, et al. Subsurface and outcrop characterization of large tidally influenced point bars of the Cretaceous McMurray Formation (Alberta, Canada)[J]. Sedimentary Geology, 2012, 279: 156-172.
Quantitative Characterization Study on Sand Body Scale in High Sinuosity Meandering River
WANG HaiFeng,FAN TingEn,SONG LaiMing,HU GuangYi,LIANG Xu,WANG Shuai,LIU XiangNan
CNOOC Research Institute, Beijing 100028, China
The meandering river sand body reservoir is important continental clastic reservoir type. Based on a series of basic data of modern high sinuosity meandering river, and the idea “past is the key to the present”, the hierarchical quantitative knowledge base was established, and underground sand body scale was characterized quantitatively. Feasibility analysis of the quantitative characterization was carried out. The study shows that the meandering river forms when the bank is mainly composed of fine material and the channel gradient ratio reduces by increasing the channel sinuosity and extending the flow path to achieve sediment transport equilibrium and the least energy consumption and. The plane geometry of meandering river channel is derivative sine curve, and the geometry and sand body scale maintain good regularity during the evolution process. Based on uncertainty of sand body scale, combining the hierarchical characterization idea of reservoir architecture theory, multiple sets of empirical formula were built hierarchically and quantitative knowledge base of high sinuosity meandering river was established by fitting the modern sedimentary data with proper confidential level. The compaction of sediment is the main factor of volume decrease of sediment after burial. Quantitative relation between modern sediment and underground sand body was built by decompaction correction. Based on these cognitions, the underground meandering river sand body scale with primary sedimentary state was characterized quantitatively. The results are objective and accurate to be proved by real data.
meandering river; high sinuosity; quantitative characterization; feasibility; uncertainty; decompaction correction
1000-0550(2017)02-0279-11
10.14027/j.cnki.cjxb.2017.02.007
2015-11-03; 收修改稿日期: 2016-03-23
中国海洋石油有限公司综合科研项目(YXKY-2014-ZY-02) [Foundation: Comprehensive Scientific Research Project of CNOOC Limited, No. YXKY-2014-ZY-02]
王海峰,男,1987年出生,硕士,工程师,沉积岩石学及岩相古地理,E-mail:whfupc@sina.cn
P512.2
A
