机电－电磁暂态混合仿真复合非对称故障计算方法

2017-04-14肖湘宁甄晓晨新能源电力系统国家重点实验室华北电力大学北京006国网石家庄供电公司河北石家庄050000

电力工程技术 2017年2期

杨洋，肖湘宁，甄晓晨（.新能源电力系统国家重点实验室（华北电力大学），北京006；.国网石家庄供电公司，河北石家庄050000）

杨洋1，肖湘宁1，甄晓晨2
（1.新能源电力系统国家重点实验室（华北电力大学），北京102206；2.国网石家庄供电公司，河北石家庄050000）

为了提高机电－电磁暂态混合仿真对机电侧非对称故障的处理能力，进一步提升混合仿真对各类工况的适应性，本文提出了一种同时考虑机电侧非对称故障和电磁侧非对称故障的计算方法。首先提出了一种机电侧发生非对称故障后的机电侧故障仿真方法，该方法根据非对称故障的类型获取故障电路导纳矩阵，继而通过修改与故障节点相关的导纳元素，将故障电路导纳矩阵的叠加到原导纳矩阵中获得故障后的导纳矩阵，并通过求解网络方程获得故障后的网络解。然后根据线性电路叠加定理，提出了接口节点戴维南等值电势的计算方法。为减少电磁侧的建模量，采用接口正序等值导纳进行戴维南电势向诺顿等值电流的转化。最后结合含有一回直流线路的IEEE39节点系统的基于PSCAD＋C架构的机电－电磁暂态混合仿真平台，验证了所提方法的精度和有效性。

机电－电磁；混合仿真；非对称故障；计算方法；精度

0 引言

近年来随着我国直流工程陆续投运，多直流、多落点、强耦合的交直流输电格局已经形成［1－4］。传统LCC⁃HVDC直流系统具有输送功率大、造价相对较低的特点，但是由于换流母线电压降低、电压不对称等因素造成的换相失败也为直流安全稳定运行埋下隐患［5，6］。非对称故障占电力系统故障的90%以上［7］，在引起直流换相失败的原因中，逆变侧交流系统非对称故障是其中的主要因素，近年来由其引起的直流换相失败和短时间内多次换相失败时有发生［8，9］。如何恰当地对这类交流系统故障引起的直流换相失败问题进行仿真，是电力系统混合仿真技术的客观需要。

机电－电磁暂态混合仿真综合了机电暂态仿真规模化建模以及电磁暂态仿真精细建模的传统优势，又避免了各自的准稳态模型不精确以及仿真资源需求过多的内在不足，较好地处理了仿真规模和仿真精度的矛盾，尤其适合大规模交直流电网的仿真分析［10］。传统的机电－电磁暂态混合仿真的研究往往重点关注于电磁侧的仿真，涉及等值形式［11，12］、接口电路宽频等值［13，14］、相量提取算法及精度［15］等，这类研究的关注点在于电磁侧故障之后直流系统或柔性交流输电系统（FACTS）装置的动态行为，而对机电侧故障以及机电侧和电磁侧同时发生的复合故障研究鲜见报道。文献［16］研究了混合仿真机电侧仿真方法，提出当机电侧故障节点与接口节点的电气距离小于1.6时，可以认为不用切换频率相关网络等值（frequency dependent network equivalent，FDNE）电路，但是没有给出机电侧故障仿真的实现形式，而且所研究的故障也不是非对称故障。

本文分析了机电侧非对称故障的计算方法，提出了机电侧非对称故障后的接口节点诺顿等值电流的计算流程，并通过含有一回直流的IEEE39节点系统机电－电磁暂态混合仿真验证了所提方法在处理机电侧和电磁侧复合非对称故障方面的精度和合理性。

1 机电侧非对称故障计算

设机电侧为一个含有N节点的系统，则存在下列节点导纳方程：

其中：Y为（3×N）×（3×N）阶方程；Yx为N×N维矩阵；Ux和Ix都为N×1维矩阵。式（1）中，电磁侧系统在机电侧等值为三序分立注入的电流源，各序电流分别考虑进I0，I1和I2中，接口节点的电压作为状态变量参与机电侧的计算。

设某时刻在p点发生非对称故障，则Y矩阵的变化如图1所示：

当机电侧系统没有发生非对称故障时，圆点位置的元素均为零，此时各序解耦可以分立求解，由于非对称故障发生，圆点位置出现了非零元素，各序之间不再解耦，Y矩阵元素的修改量为：

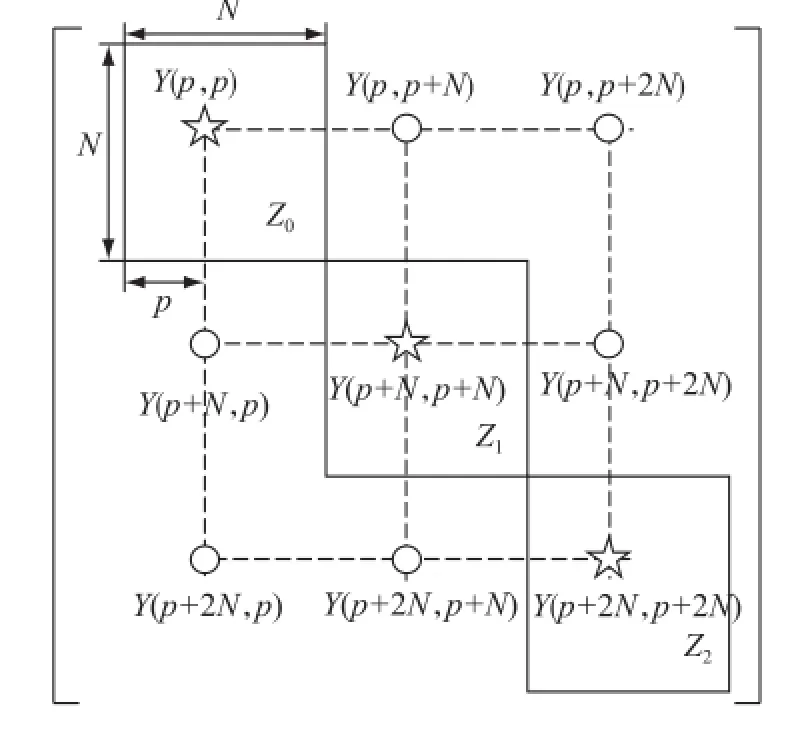
图1 Y矩阵的变化Fig.1 The change of Y matrix

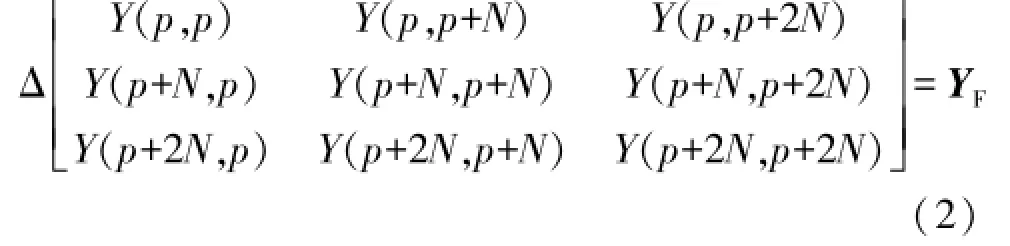
YF为非对称故障电路对应的序分量形式表示的故障导纳矩阵，不同的非对称故障对应不同的故障导纳形式，三类典型非对称故障的故障电路如图2所示。

图2 三种典型非对称故障的故障电路Fig.2 Diagrams of fault circuits of three typical asymmetrical faults

图2 中单相接地故障、两相接地故障和两相短路故障的故障导纳矩阵的序分量形式分别为：

单相断线故障和两相断线故障分别与ZF＝0时的两相金属性接地短路故障和单相金属性接地故障的故障导纳矩阵一致。

经过对故障前导纳矩阵的修改，可以求得故障后的网络节点电压为：

可知，机电侧进行正常情况和故障期间计算的主要差别在于所采用的导纳矩阵以及相应的阻抗矩阵不同。正常情况下，三序导纳矩阵以及等值阻抗矩阵解耦，因此各序的电压只与本序对应的电流激励相关，三序导纳阵的求逆可以转化为3个独立的序导纳矩阵的求逆。当系统发生非对称故障尤其考虑接地的非对称故障之后，故障导纳矩阵中三序导纳阵相互之间不再解耦，经过矩阵求逆之后的等值阻抗阵也不再是3个独立的矩阵，而一般是3N ×3N（N是节点数目，这里不考虑零序导纳阵的规模）的满阵。此时，某一序的节点电压不仅与本序的电流激励相关，还可能与其他两序的电流激励相关。在电力系统中，式（6）右侧电流相量的非零元素主要包括发电机注入电流、电动机注入电流、负荷的电流和功率部分等，后者主要以正序电流为主，因此故障后某个节点某一序的节点电压与对应的该节点和上述三类节点之间该序下的互阻抗以及注入的电流相关。从而，式（6）可以相应简化，当仅考虑发电机注入的正序电流时，式（6）可以表示为：

其中：Zxsf表示故障情况下某序下节点与发电机节点之间的互阻抗矩阵，其维数为N×Ns维，N是系统总的节点数目，Ns是系统内发电机节点数目。

2 接口诺顿等值电流形成和计算

对于接口节点戴维南等值电压，有计算公式如式（8）所示：

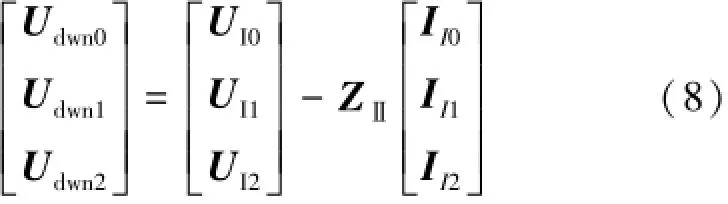
其中：ZⅡ为接口三序等值阻抗矩阵，在机电侧没有发生接地故障时，式（1）的三序独立，如果电磁侧发生非对称故障而向机电侧注入负序或零序电流，可知对于机电侧而言，接口的负序和零序电流是唯一的电源激励，因此UI0＝ZⅡ0II0，UI2＝ZⅡ2II2，Udwn0和Udwn2均为零，戴维南等值电势转化为Udwn1＝UI1－ZⅡ1II1，为正序等值。

当机电侧发生非对称故障后，式（8）中的ZⅡ也发生变化，理论上戴维南等值电势的计算方法为：

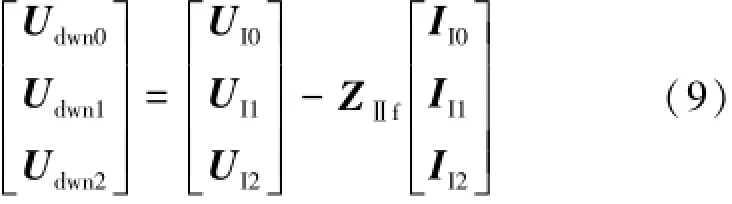
其中：ZⅡf为机电侧发生故障后接口的序等值阻抗矩阵。按此式计算戴维南等值电势，则在电磁侧的等值电路也要相应进行切换。

由式（7），并考虑接口注入电流，接口电压的表达式为：

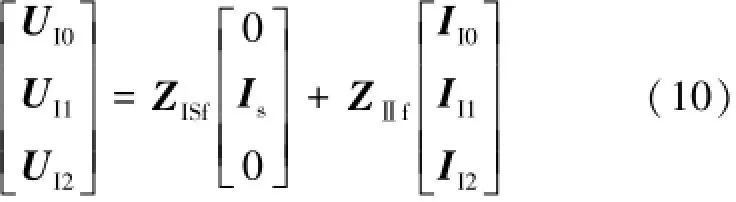
其中：ZISf是接口节点与发电机节点之间的三序互阻抗矩阵，带入式（9）可得：

也就是，故障后接口戴维南电势的大小只与发电机注入电流和发电机与接口节点之间的互阻抗矩阵相关，而与接口节点注入电流无关。此时将戴维南电势转化为诺顿等值电流可得：

定义为端口－发电机故障情况下的等效互导纳阵，其值为端口互阻抗矩阵的逆矩阵与端口－发电机阻抗矩阵的积。

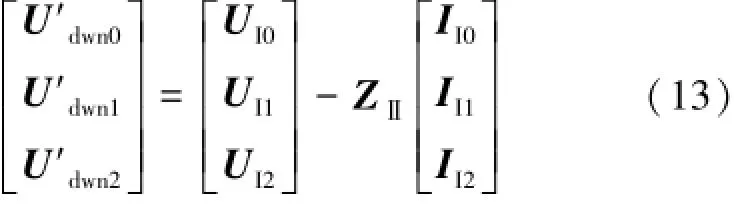
当接口数目较多时，电磁侧接口电路的切换将十分复杂。为减少电磁侧建模复杂度，无论机电侧是否发生非对称故障，式（9）均表示为：也就是无论机电侧是否发生节点故障或者其他接线方式的变化，戴维南电势的求取始终采用系统正常运行时的各序等值阻抗矩阵。将式（10）带入式（13）可得：

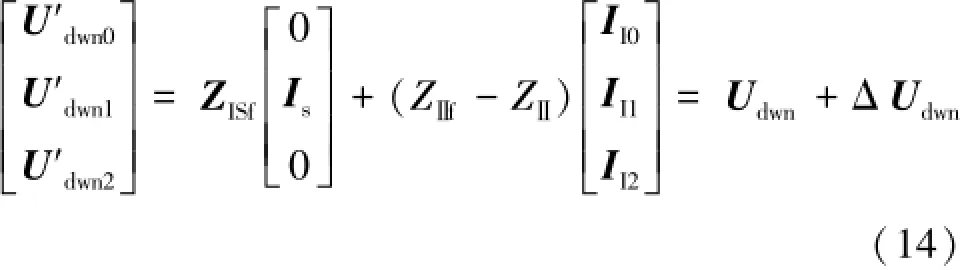
此时，诺顿等值电流为：

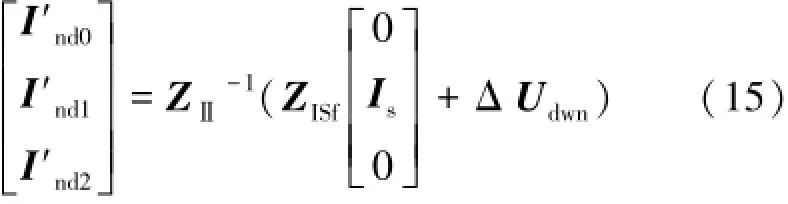
比较式（11）和式（14）可知，当考虑电磁侧电路切换时，接口节点的戴维南电势的表达式仅与发电机注入电流和端口阻抗矩阵以及端口－发电机互阻抗矩阵相关，此时仅仅需要向机电侧传递接口正序电流即可以完成交互步长的计算和戴维南电势的求取。当不考虑电磁侧电路切换时，戴维南电势同时取决于发电机注入电流、接口阻抗矩阵、接口－发电机互阻抗矩阵以及接口各序注入电流。因此如果采用式（11）进行戴维南等值电势的求取，可以不用考虑接口负序和零序注入电流；但如果采用式（14）进行戴维南电势求取，则需考虑接口注入负序和零序电流。前者传递的信息较少，但是电路建模复杂；后者传递的信息稍多，但接口电路建模稍简单，减少了电磁侧的建模复杂度，增加仿真方式的灵活性。另一方面，从第二部分仿真结果的比较可知，这种方式带来的误差较小，能够满足对精度的需求。

进一步将诺顿电流转化为ABC三相的形式有：

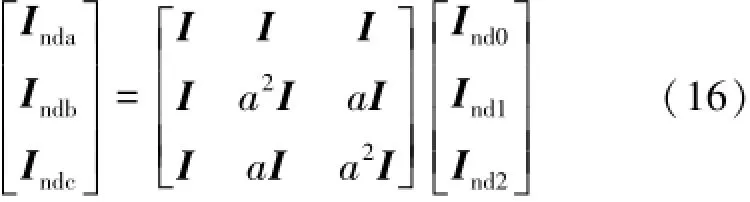
其中：I为N×N维单位矩阵，a＝ej2π／3。

在式（6）的机电暂态计算过程中同时考虑由于机电侧故障带来的节点侧节点导纳变化以及由于可能的电磁侧故障引起的接口注入电流变化，因此这种计算方式可以同时处理机电侧和电磁侧的各类故障，从而具备了对复合故障的处理能力。考虑机电侧故障后的机电侧计算流程如图3所示。

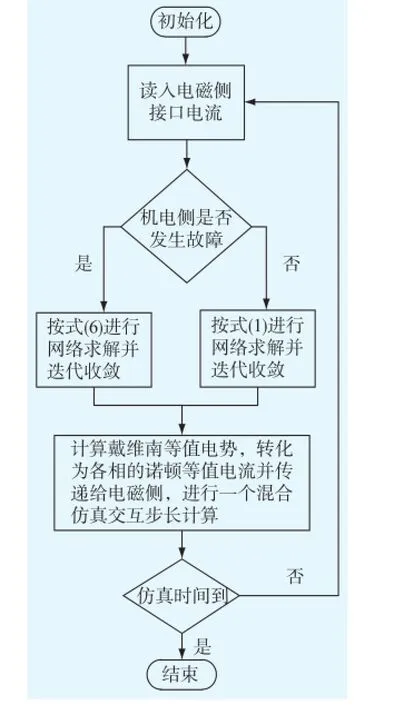
图3 考虑机电侧故障的机电侧计算流程Fig.3 Electromechanical side calculation procedure considering faults occurring in the electromechanical side

为了提高仿真效率，在正常和故障计算中用到的阻抗矩阵都在仿真初始化期间计算完成，仿真过程中根据需要直接调用即可。

3 仿真验证

在PSCAD／EMTDC中建立如图4所示基于PSCAD＋C架构的机电－电磁暂态仿真模型，将新英格兰39节点系统中的第39节点的发电机替换为直流输电线路，直流的逆变侧接入39节点，并选择39母线为接口母线。直流模型参数及控制方式参见CIGRE标准直流模型［17］，发电机采用六阶模型，负荷采用恒阻抗模型，直流系统在电磁暂态侧仿真，交流系统在机电侧系统仿真。机电侧仿真步长设定为10 ms，电磁侧仿真步长设定为50 μs，交互周期设定为10 ms。对本文提出的处理复合故障的计算方法进行验证。

3.1处理电磁侧非对称故障能力的验证

电磁侧发生非对称故障后，以零序、正序和负序等值电流的形式传递给机电侧进行机电暂态求解。电磁侧三序电流的作用对象主要针对式（1）右侧的电流列向量，由于此时机电侧没有发生故障，因此机电侧采用正常运行时的节点阻抗矩阵进行计算，各序的计算仍然解耦。设t＝5 s时在直流逆变侧发生A相金属性短路故障。直流逆变侧功率和36号发电机转速如图5所示。

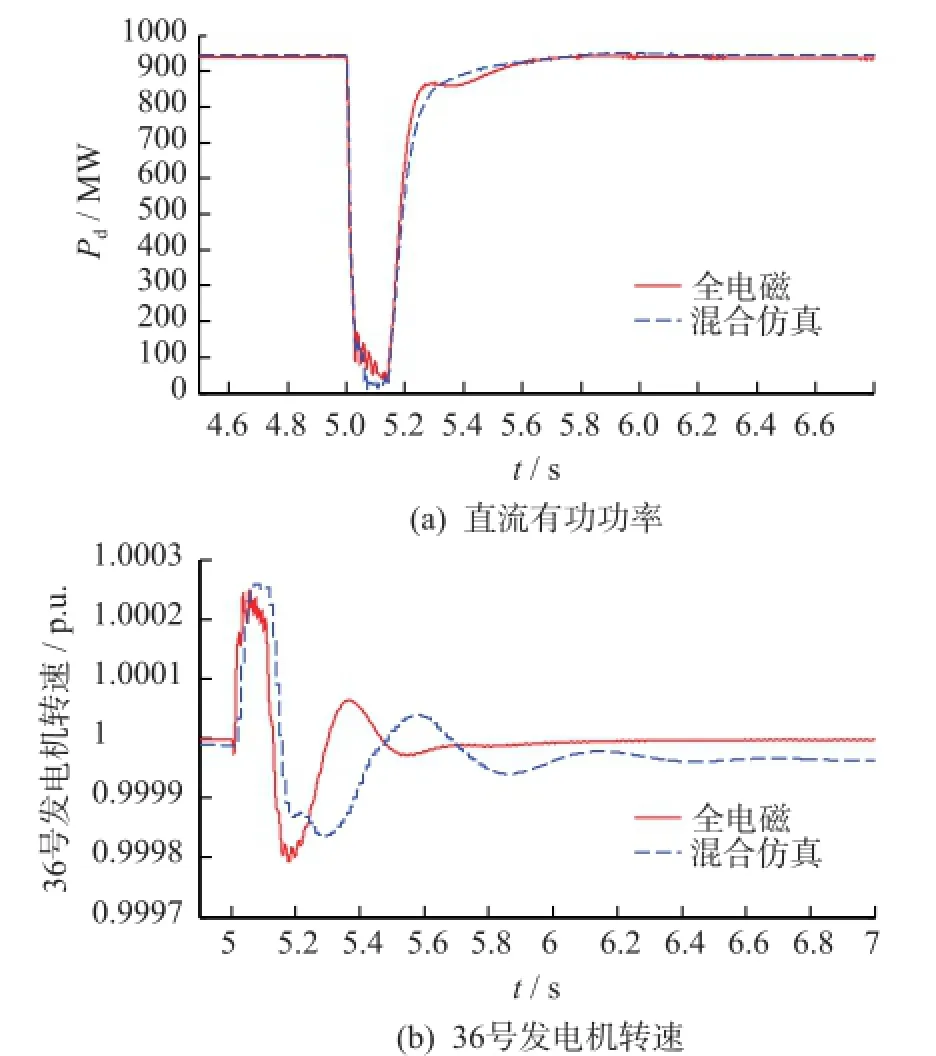
图5 只考虑电磁侧非对称故障的仿真结果Fig.5 Simulation results only considering electromagnetic side asymmetric fault

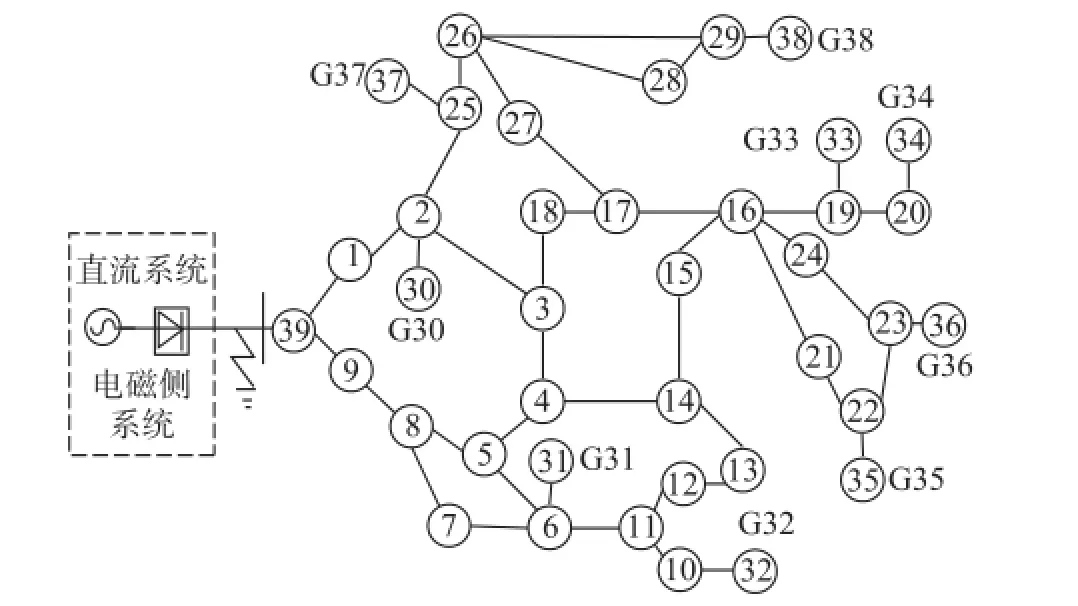
图4 含有一回直流的IEEE39节点系统Fig.4 IEEE 39 system with a DC link

如图5（a）所示，在故障期间和故障清除后混合仿真得到的直流功率变化与全电磁暂态仿真基本一致；5（b）中发电机转速在最大值与全电磁暂态仿真基本相同，故障清除后发电机转速的变化曲线的相位与全电磁有所差异，但转速偏差量的衰减速度与全电磁仿真基本相似，最终均达到稳态，整体上当电磁侧发生非对称故障后，混合仿真与全电磁暂态仿真均有较为相似的仿真结果，说明当电磁侧故障后，所提计算方法具有较好的仿真精度。

比较全电磁仿真与混合仿真计算时间。启动到稳态、稳态运行和故障的仿真时间分别为1 s，4 s，0.1 s，分别采用全电磁仿真和混合仿真所用的计算时间如表1所示（计算机配置为Intel（R）Core（TM）i3－2310M CPU＠2.10 GHz，内存2 GB（RAM））。

表1 全电磁与混合仿真计算时间对比Table 1 Comparison of calculation time between full electromagnetic and hybrid transient simulation

从表1可见，混合仿真比全电磁仿真从启动开始更快地进入稳态，在稳态期间具有较高的仿真速度，能更快地处理电磁侧的暂态故障，混合仿真相对于全电磁暂态仿真在计算效率方面具有显著的优势。

3.2处理机电侧非对称故障能力的验证

验证处理机电侧非对称故障的能力。设t＝5 s时在第8节点发生AB相经0.1 Ω电阻相间短路故障，直流逆变侧功率和36号发电机转速如图6所示。

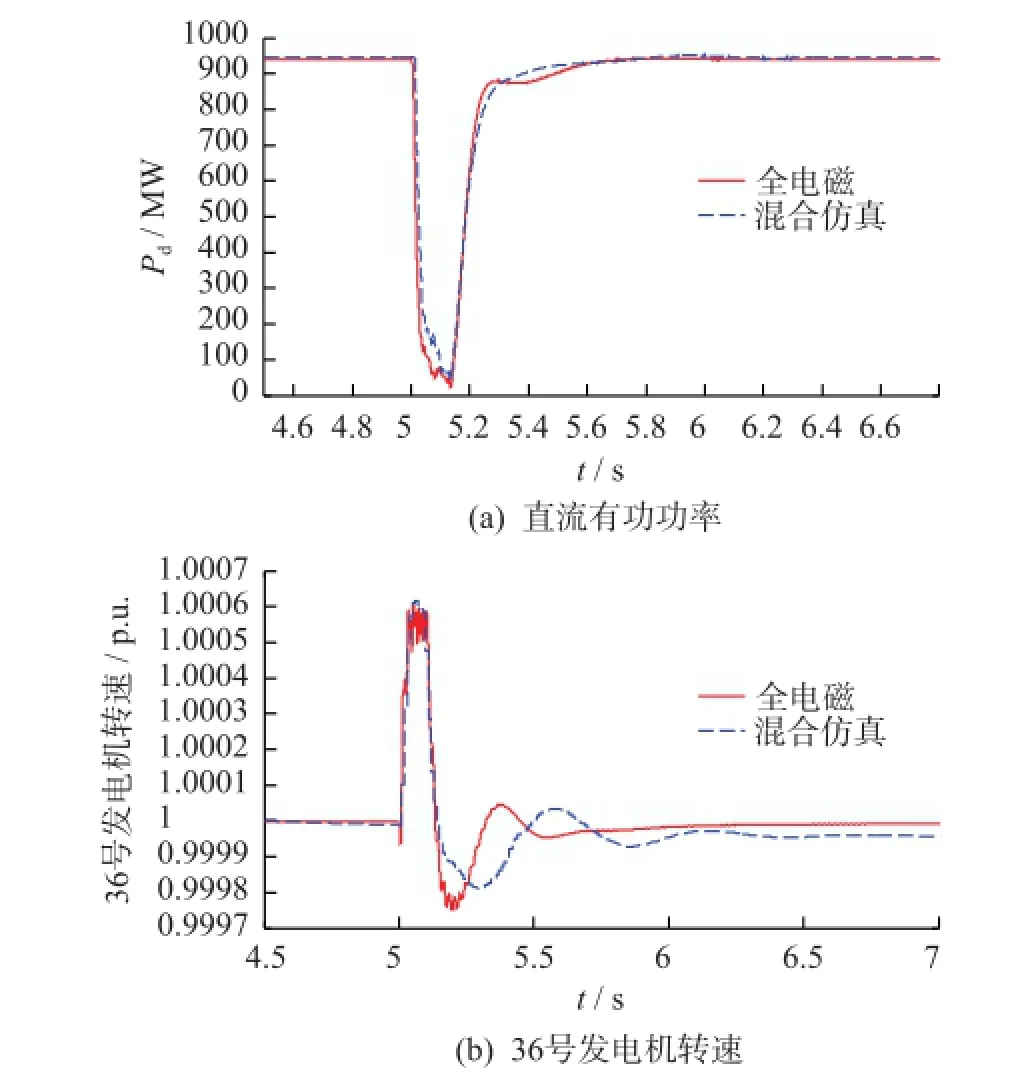
图6 只考虑机电侧故障的仿真结果Fig.6 Simulation results only considering electromechanical side asymmetric fault

从图6（a）可见，故障期间直流输送有功功率接近零，交流故障引起了直流换相失败，说明混合仿真对由机电侧故障引起的直流换相失败现象的仿真是有效的；从图6（b）可见，故障期间发电机转速的最大值与全电磁一致，尽管故障清除后发电机转速变化曲线摆动的相位存在一定差异，但故障后发电机转速与额定值差异量的衰减速度基本一致，并且最后均达到稳定。通过在机电侧设置AB相相间短路故障，验证了混合仿真对机电侧故障的处理能力。当故障发生在机电侧时，故障期间混合仿真的加速比为TM／TH＝5.04／0.38＝13.26，相比故障设置在电磁侧的情况（TM／TH＝3.49），混合仿真可以获得更大的加速比。

3.3同时处理机电侧和电磁侧同时发生非对称故障能力的验证

进一步验证混合仿真同时处理机电侧和电磁侧非对称故障的能力。设t＝5 s时电磁侧的直流逆变侧交流母线发生金属性三相接地故障，与此同时机电侧发生经0.1 Ω电阻AB相间短路故障，直流逆变侧功率和36号发电机转速如图7所示。为了进行比较，同时显示了考虑电磁侧等值电路切换的仿真效果。等值电路切换仿真方法见文献［16］。

图7 同时考虑机电侧和电磁侧非对称故障的仿真结果Fig.7 Simulation results only both considering electromagnetic and electromechanical side asymmetric faults

从图7（a）可见，故障期间，直流功率接近为零，混合仿真与全电磁仿真具有较好的契合度。故障期间混合仿真对应的发电机转速略高于全电磁仿真，故障清除后发电机转速变化曲线的相位与全电磁有所差异，但总体趋势与全电磁一致，最终二者均趋于稳定。考虑电路切换的仿真结果与未考虑电路切换的仿真结果基本一致，说明在进行机电侧故障仿真时可以不考虑机电侧故障给电磁侧等值电路带来的变化，而仅通过诺顿等值电流补偿电路变化带来的影响。机电侧和电磁侧故障的仿真验证了混合仿真对机电侧和电磁侧同时故障的复合故障的处理能力。故障同时发生在机电侧和电磁时，故障期间混合仿真的加速比为TM／TH＝7.72／1.58＝4.89，介于故障设置在电磁侧和机电侧之间。

需要指出，当接口数目不唯一，接口电路相对复杂时，采用式（13）和式（14）计算出的诺顿等值电流仍然可以保持相对较高的仿真精度。仍以图4所示的系统为例，接口位置选择在2－8节点，包含直流、1、9节点的系统在电磁侧仿真，剩余部分在机电侧仿真，此时接口数目为2个。设定在t＝5 s时在节点8位置发生AB相经0.1 Ω电阻短路故障，直流功率和36号发电机转速如图8所示。

图8 采用两个端口且不考虑非对称故障期间接口电路切换时的仿真结果Fig.8 Simulation results using two ports without interface circuit switching during asymmetric fault

比较图8和图4在故障期间的仿真结果可知，2个端口的情况下，故障位置与接口存在一定电气距离，如果不考虑故障期间的电路切换，相比于接口位置单一且近故障点的情况，其仿真精度略为下降，但整体上与全电磁暂态仿真仍然较为接近，从而进一步说明在故障期间采用式（13）、（14）计算诺顿等值电流的可行性。

4 结语

本文提出了一种处理机电－电磁暂态混合仿真机电侧和电磁侧非对称复合故障的计算流程和方法。首先分析了机电侧计算非对称故障的计算过程，然后结合接口节点的电压解和等值阻抗矩阵提出各序戴维南等值电势的计算方法，为了减小电磁侧接口电路的复杂程度并提高混合仿真对机电侧故障的适应性，提出采用稳态等值阻抗计算戴维南电势和诺顿等值电流的方法。结合含有一回直流的IEEE39节点系统，通过分别在电磁侧、机电侧以及机电侧和电磁侧同时设置非对称故障，验证了本文所提方法的精度和合理性。

对比了启动到稳态，稳态运行和故障期间全电磁仿真和混合仿真的计算时间。结果表明，混合仿真在计算效率上比全电磁仿真具有显著优势，并且故障设置在机电侧比故障设置在电磁侧在故障期间具有更大的加速比。

［1］覃琴，郭强，周勤勇，等.国网“十三·五”规划电网面临的安全稳定问题及对策［J］.中国电力，2015，48（1）：25－32.

QIN Qin，GUO Qiang，ZHOU Qinyong，et al.The security and stability of power grids in 13 th Five⁃Year planning and counter⁃measures［J］.Electric Power，2015，48（1）：25－32.

［2］国家电网公司.国家电网公司“十二·五”电网发展规划［R］.北京：国家电网公司，2012. State Grid Corporation.State grid corporation“Twelf⁃Five”power grid development plan［R］.Beijign：State Grid Corporation，2012.

［3］刘振亚，张启平.国家电网发展模式研究［J］.中国电机工程学报，2013，33（7）：1－10.

LIU Zhenya，ZHANG Qiping.Study on the development mode of national power grid of China［J］.Proceedings of the CSEE，2013，33（7）：1－10.

［4］刘振亚.特高压电网［M］.北京：中国经济出版社，2005：159－166.

LIU Zhenya.Ultra high voltage grid［M］.Beijing：China Eco⁃nomic Press，2005：159－166.

［5］朱鑫要，汪惟源，汪成根.江苏特高压交直流输电交互影响研究［J］.江苏电机工程，2016，35（2）：39－42.

ZHU Xinyao，WANG Weiyuan，WANG Chenggen.Analysis of interaction between UHVAC and UHVDC for Jiangsu Power Grid［J］.Jiangsu Electrical Engineering，2016，35（2）：39－42.

［6］欧开健，任震，荆勇.直流输电系统换相失败的研究（一）——换相失败的影响因素分析［J］.电力自动化设备，2003，23（5）：5－8. OU Kaijian，REN Zhen，JING Yong.Research on commutation failure in HVDC transmission system Part 1：Commutation failure factors analysis［J］.Electric Power Automation Equip⁃ment，2003，23（5）：5－8.

［7］VAAHEDI E，LI W，CHIA T，et al.Large scale probabilistic transient stability assessment using BC Hydro s on⁃line tool［J］. IEEE Transactions on Power Systems，2000，15（2）：661－667.

［8］李新年，易俊，李柏青，等.直流输电系统换相失败仿真分析及运行情况统计［J］.电网技术，2012，36（6）：266－271.

LI Xinnian，YI Jun，LI Baiqing，et al.Simulation analysis and operation statistics of commutation failure in HVDC transmission system［J］.Power System Technology，2012，36（6）：266－271.

［9］王晶，梁志峰，江木，等.多馈入直流同时换相失败案例分析及仿真计算［J］.电力系统自动化，2015，39（4）：141－146.

WANG Jing，LIANG Zhifeng，JIANG Mu，et al.Case analysis and simulation of commutation failure in multi⁃infeed HVDC transmission systems［J］.AutomationofElectricPower Systems，2015，39（4）：141－146.

［10］SU Hongtian.Real⁃time electromagnetic electromechanical hy⁃brid transient simulation for large power systems［D］.Hong Kong：Hong Kong Polytechnic University，2005.

［11］杨洋，肖湘宁，陶顺，等.混合仿真电磁侧功率源等效误差原理分析及改进［J］.电力系统自动化，2015，39（24）：104－109.

YANG Yang，XIAO Xiangning，TAO Shun，et al.Electromag⁃netic side power source equivalent error principle analysis and its improvement for hybrid simulation［J］.Automation of Elec⁃tric Power Systems，2015，39（24）：104－109.

［12］肖湘宁，杨洋，陶顺，等.混合仿真电流源等值误差机理分析及改进［J］.电力建设，2016，37（6）：38－42.

XIAO Xiangning，YANG Yang，TAO Shun，et al.Current sourceequivalenterrormechanismanalysisandits improvement for hybrid simulation［J］.Electric Power Con⁃struction，2016，37（6）：38－42.

［13］张怡，吴文传，张伯明，等.基于频率相关网络等值的电磁－机电暂态解耦混合仿真［J］.中国电机工程学报，2012，32（16）：107－114.

ZHANG Yi，WUWenchuan，ZHANGBoming，etal. Frequency dependent network equivalent based electromagnetic and electromechanical decoupled hybrid simulation［J］.Pro⁃ceedings of the CSEE，2012，32（16）：107－114.

［14］LIN Xi，GOLE A M，YU Ming.A wide⁃band multi⁃port system equivalent for real⁃time digital power system simulators［J］. IEEE Transactions on Power Systems，2009，24（1）：237－249

［15］杨洋，肖湘宁，陶顺，等.考虑衰减直流分量的dq⁃120改进算法及其在混合仿真中的应用［J］.电力建设，2016，37（6）：43－48.

YANG Yang，XIAO Xiangning，TAO Shun，et al.An improved dq⁃120 algorithm considering decaying DC component and Its application in hybrid simulation［J］.Electric Power Construc⁃tion，2016，37（6）：43－48.

［16］张怡，吴文传，张伯明，等.电磁－机电暂态混合仿真中机电侧故障的仿真方法［J］.中国电机工程学报，2012，32（19）：81－88.

ZHANG Yi，WU Wenchuan，ZHANG Boming，et al.Simula⁃tion method of faults on electromechanical side in electromag⁃netic and electromechanical hybrid simulation［J］.Proceedings of the CSEE，2012，32（19）：81－88.

［17］邓广静，周威.CIGRE直流输电标准模型的建模及控制策略仿真研究［J］.江苏电机工程，2009，28（1）：31－34.

DENG Guangjing，ZHOU Wei.Study on modeling and control strategy of CIGRE HVDC benchmark system［J］.Jiangsu Elec⁃trical Engineering，2009，28（1）：31－34.

Calculation Method of Complex Asymmetrical Fault
in Electromechanical and Electromagnetic Transient Hybrid Simulation

YANG Yang1，XIAO Xiangning1，ZHEN Xiaochen2
（1.State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources North China Electric Power University（NCEPU），Beijing 102206，China；2.State Grid Shijiazhuang Power Supply Company，Shijiazhuang 050000，China）

To improve the processing ability of asymmetrical eletromechanical side fault as well as the flexibility of electromechanical and electromagnetic transient hybrid simulation，a calculation method of complex asymmetrical fault in the electromechanical and electromagnetic side at the same time is proposed.This method obtains the fault circuit admittance matrix according to the type of asymmetric fault.By modifying the admittance element associated with the faulty node，the fault circuit admittance matrix is superimposed on the normal admittance matrix to obtain the admittance matrix after fault.The network solution is finally achieved by solving the network equation after fault.Based on the linear circuit superposition theorem，the Thevenin equivalent voltage of the interface node is calculated.To reduce the modeling scale of the electromagnetic side，positive sequence equivalent conductance of the interface is used for the conversion of the Thevenin equivalent voltage into Norton equivalent current.At last，through the electromechanical and electromagnetic transient hybrid simulation platform of a IEEE 39 system containing a HVDC line based on PSCAD＋C frame，the simulation accuracy and effectiveness of the method is validated.

Electromechanical and electromagnetic；hybrid simulation；asymmetrical Fault；accuracy

TM73

：A

：2096－3203（2017）02－0014－07