模块化多电平换流器电容电压均衡排序算法综述
2017-04-14赵成勇许建中
熊 岩,赵成勇,许建中
(新能源电力系统国家重点实验室(华北电力大学),北京102206)
·专论与综述·
模块化多电平换流器电容电压均衡排序算法综述
熊 岩,赵成勇,许建中
(新能源电力系统国家重点实验室(华北电力大学),北京102206)
高压大容量模块化多电平换流器(modular multilevel converter,MMC)在世界的柔性直流输电工程得到了广泛的应用,有关MMC的电容电压均衡排序算法已成为研究热点与难点。论文针对适合高电平的MMC电容电压均衡排序算法,对国内外已有的涉及排序算法的主要文献进行整理和归纳,从而探索该领域的研究前沿和关注的重点。将不同的均压排序算法根据降低计算复杂度、降低器件开关频率等优化目的进行了分类,并研究了其核心思想;探讨了MMC电容电压均衡排序算法评价指标;对其中降低复杂度的3种均压排序方法的排序复杂度进行比较,且通过仿真对比了它们的电容电压均衡效果;对其中采用保持因子降低开关频率的排序方法进行了比较。最后,针对MMC实时仿真,讨论了均衡排序算法的发展方向。
模块化多电平换流器;均压排序算法;分组排序;时间复杂度;器件开关频率;实时仿真
0 引言
模块化多电平换流器(modular multilevel con⁃verter,MMC)因其在有功功率和无功功率独立控制,新能源接入、异步联网及城市供电等方面的独特优势,已成为柔性直流输电系统的首选换流器拓扑[1-3],在世界范围内取得了广泛的应用[4,5]。我国正在建设的张北四端柔直工程、渝鄂异步联网工程、广东电网东西异步联网工程[1]也将采用MMC结构。MMC已由最初的低电压、小容量示范工程向高电压、大容量和多端系统的方向快速发展,展现出良好的发展前景。
在MMC控制系统中,子模块电容电压均衡控制策略是关键技术与难点之一,目前有关的研究也较为广泛。现有文献中采取的方法可分为实时采集子模块电容电压排序与应用载波移相调制技术两大类传统均压算法[6],但载波移相调制技术不适用于高电平MMC系统。高压大容量的柔性直流输电系统中,每个换流器中的子模块数目成百上千,传统的子模块电容电压均衡排序算法[7,8]的时间复杂度高,计算量巨大,给硬件实现带来严重的挑战,并且采用传统均压算法子模块投切频繁,换流器损耗高,影响器件的使用寿命。目前诸多优化的子模块电容电压排序算法降低了传统排序算法的时间计算复杂度和子模块的投切频率(器件开关频率)。本文根据优化算法的目的和效果将现有的子模块电容电压均衡排序算法分为3种类型:A型、B型和AB型。A型排序算法只降低排序算法的排序复杂度,该类排序算法的核心思想是尽可能将子模块进行分组排序;B型排序算法只降低绝缘栅双极型晶体管(IGBT)等器件的开关频率从而降低损耗,本质是避免子模块的频繁投切;AB型排序算法能够同时降低排序算法的计算复杂度和IGBT等器件的开关频率。柔性直流输电系统在工程投运之前,保护控制策略等往往需要经过实时仿真验证后才能投入使用。实时仿真相比离线仿真对硬件要求更高,故对均压排序算法时间复杂度要求越低越好。
本文主要研究适用于高电平MMC的排序均压算法,将优化的均压算法进行分类归纳,对比几种典型的均压排序算法的均压效果,探讨了评价均压排序算法的指标,讨论实时仿真硬件对排序算法的要求和未来的排序算法的发展方向。
1 MMC基本结构与传统均压策略
1.1 MMC基本结构
MMC是由德国慕尼黑联邦国防大学的教授Rainer Marquardt在2002年提出[9]。图1所示为三相MMC的通用结构,共包含6个桥臂,每个桥臂包含N个子模块和1个桥臂电感L。桥臂电感作为连接电感的一部分,可以抑制因子模块电容电压波动而造成的相间环流,同时还可有效抑制直流母线发生短路故障时的冲击电流[10]。文献[10,11]介绍了MMC的基本运行原理及MMC-HVDC的控制策略。
每个子模块由2个IGBT开关器件,2个反并联二极管和1个直流存储电容构成,并且存在投入、旁路和闭锁3种开关状态。通过2个开关器件T1和T2工作状态的切换,子模块输出电压USM可以在UC和0之间切换。通过触发导通上下桥臂不同的子模块数量,使得交流侧输出多电平波形。

图1 三相MMC结构图Fig.1 Schematic of a three⁃phase MMC
1.2基于NLM的传统均压策略
目前较为常用的MMC调制策略分为脉宽调制(PWM)方式和阶梯波调制方式[12]。PWM调制策略主要包括载波移相脉宽调制(carrier phase shifted⁃SPWM,CPS-SPWM)、载波层叠脉宽调制和空间矢量脉宽调制[13-16]。而阶梯波调制具体实现方式分为特定次谐波消去阶梯波调制和最近电平逼近调制(nearest level modulation,NLM)[17,18]。NLM因开关频率小,实现方式简单应用最为广泛,且适用于高电平MMC换流器。
具体实现过程为:假设每相上下桥臂均含有n个子模块,正常运行时要求每相投入的子模块总数保持为n不变。上桥臂投入子模块个数nup和下桥臂投入子模块个数ndown可以分别表示如下:
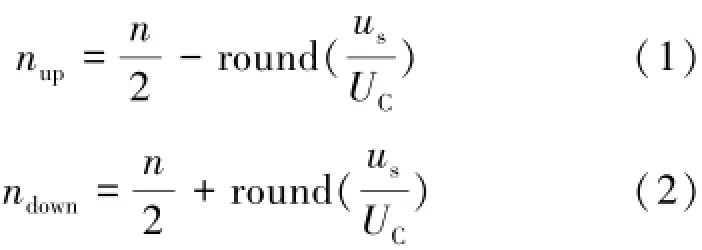
式中:us表示调制波电压;UC表示单个子模块电容电压;round表示按四舍五入取整。
在传统电容电压平衡方法中[10,11],首先监测每个子模块电容电压值,采用冒泡法进行排序。当桥臂电流大于零时,桥臂电流对子模块电容进行充电,根据所需投入的子模块个数按从小到大的顺序投入子模块;当桥臂电流小于零时,桥臂电流对子模块进行放电,根据所需投入的子模块个数按从大到小的顺序投入子模块。当采用传统冒泡排序方法时,对含有n个子模块的桥臂进行一次排序所需排序次数如下所示:

式中:T0为最大时间复杂度下的排序次数。
传统的排序算法(冒泡法)具有很好的均压效果,子模块间电容电压值偏差小,但时间复杂度高,子模块投切频繁,故国内外学者对其从不同角度进行了优化改进。
2 高电平MMC均压排序算法
本文将高电平MMC均压排序算法根据其优化的目的分为3种类型:文献[19-23]中的算法属于上文中的A型均压排序算法,与传统均压排序算法相比只降低排序算法的复杂度,其核心思想为将子模块进行分组处理[19-23]。文献[24-31]中的算法属于B型均压排序算法,与传统均压排序算法相比只降低器件的开关频率,通过乘以保持因子或设置电容电压上下限来保持子模块的原有状态从而避免子模块频繁投切。文献[32-38]中的算法属于AB型均压排序算法,与传统均压排序算法相比既降低了时间复杂度,又降低了器件的开关频率。
2.1 A型(降复杂度)均压排序算法
将采集的MMC子模块电容电压进行排序的过程中,若将若干子模块分为多组进行排序,能够降低排序算法的时间复杂度。通过质因子分解法对子模块进行分组是最优的分组方法,组内仍然采用冒泡法排序,组间平衡采取改进的方法[19]。以质因子分组后排序的时间复杂度为:
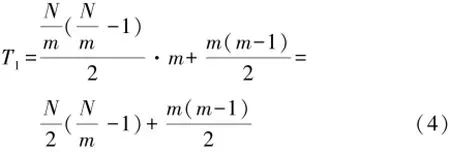
式中:N为每个桥臂子模块个数;m为分组的数量。将式(4)与式(3)进行比较可以看出,文献[19]中的算法比冒泡法复杂度降低很多。文献[20]在质因子分组的基础上在组内和组间平衡时都引入希尔排序算法,称为混合排序法,相比冒泡法可以有效减少排序次数。在质因子分同样组数的情况下,随着分组层数增加,质因子系数减小,混合排序相较于质因子排序法的优化效率将会随之降低[20]。从文献[20]仿真的排序次数拟合结果为N1.28,又因为希尔排序算法的排序复杂度不超过N log2N,可以得知混合排序法时间复杂度为:

式中:N表示子模块个数。当N≥3时,式(5)中小于号恒成立,故T2<N log2N。混合排序算法比质因子分解法排序时间复杂度更低,排序复杂度为O(N log2N),相对冒泡排序法O(N2)大大降低。其中符号“O”是一种算法复杂度(操作的数量)的相对表示方式。这2种算法的优点是:只降低排序运算量且对MMC系统特性没有影响,均压效果与冒泡法基本无差。
文献[21]中的“分组排序”与上述文献中的分组排序不同,该文直接将子模块分为导通组和关断组2组进行交换排序[21]。该算法每次排序过程最多比较N-1次,其应用条件是MMC模型采用戴维南简化并且积分方法采用后退欧拉法,否则无法达到排序效果[21],原因是该排序算法在排序前要求开通组和关断组内的子模块电容电压序列均为严格升序排列。该算法排序复杂度超低,但是无法扩展至常规的MMC模型。文献[22]采用分布式均压,将子模块分为多组,根据桥臂电容电压平均值和各自子模块分组电容电压平均值,采用PI环节动态分配每组所需的导通个数。该方法与质因子分解法的组间平衡方法异曲同工,能有效降低运算量,但是均压效果还有待进一步验证。文献[23]成功地将桶排序理论应用于MMC排序均压。该文将N个子模块按照实际电压范围从小到大分成若干组,每组的电压上下限根据均压要求设定;然后将所有子模块遍历一次,计算每一组的子模块个数;最后根据当前控制周期的投入子模块个数,确定每个子模块是否投入。该算法在FPGA(field program gate ar⁃ray)中实现只需2N个寄存器,非常适宜硬件实现,具有很好的应用前景。
A型排序算法能够降低排序复杂度,子模块电容电压的一致性很好,排序效果与传统的排序算法基本无差,不影响MMC系统特性。
2.2 B型(降频)均压排序算法
IGBT等器件的开关损耗是MMC换流器的主要损耗之一,降低开关器件的损耗一直是研究热点。目前减少子模块投切频率的主要方法有保持因子法[25]、设置子模块电容电压的最大偏差保持法[27]和避免多余动作。
文献[24]通过对子模块电容电压平衡过程的结构分析,基于调整子模块排序时间或子模块投切时间的思想提出3种降低触发脉冲频率的电容电压平衡算法。文献[25,26]是通过设置电容电压上下限来区分子模块的状态,然后乘以一个1附近的保持因子来让子模块保持原有状态。这种方法思路简单,易于实现,目前已较为常用。文献[27]在此基础上,通过引入双保持因子,然后PI反馈控制,能将子模块的开关频率精确地控制在120 Hz附近。文献[28]通过设置子模块电容电压允许偏差值,只在子模块导通个数发生变化时,改变投入的子模块脉冲。但是电压偏差值难以确定,且对开关频率影响较大。文献[29,30]分别提出了一种电网基频排序方法,但实现过程较为繁琐。
B型排序方法面临的共同问题是:该类算法虽然降低了器件开关频率,但是相比传统的排序方法,子模块电容电压的一致性变差[25-28]。降频效果越好,电容电压的一致性越差。如何选取最合适的保持因子、偏差值成为一个需要继续研究的问题。B型算法的优劣程度不能只看降频效果,还应该综合考虑其均压效果。
文献[32]定义了电容电压总体波动系数δ和电容不平衡度ε 2个指标来评价电容电压的均衡效果,δ是子模块电容电压相对额定值的最大偏差,ε为子模块电容电压最大值与最小值之差比它们的和的一半[33]:
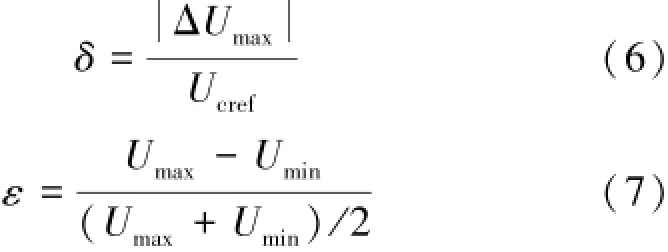
采用传统均压算法的优点是子模块电容电压的均压效果好,子模块间的最大电压偏差一般不会超过每个控制周期的电容电压的变化量,但此方法会额外增加许多附加的开关动作[33]。子模块电容电压波动的实质是能量的交换,在一个周期内,能量交换越频繁,则各子模块的一致性越好,电容的波动小且电容电压一致性越好;反之则可能引起电容电压波动幅值超过每个控制周期的变化量,电容一致性变得很差。文献[39]通过推导MMC平均开关频率的解析表达式,总结开关频率与电压偏差之间的关系,给出了最大电压偏差的取值范围,对B型排序算法的取值有一定的指导和借鉴意义。
2.3 AB型(双降)均压排序算法
部分AB型算法由A型或B型算法改进而得[31,34-36],故AB型算法集A型和B型排序算法的优点于一体,但是AB型算法存在与B型算法同样的缺点,均压效果不如传统的冒泡排序均压。最简单且普遍的一种方法是:在NLM调制下,只在导通的子模块数目发生变化时,才启动排序,改变子模块脉冲。这可以减少平均排序工作量,降低器件的开关频率[5]。
文献[31]在分组排序的基础上引入双保持因子,使其排序算法达到了降排序复杂度与降频的双重效果。将N个子模块分为m组,时间复杂度为:

文献[32]先应用与文献[23]类似的桶排序理论将子模块进行分组,然后借鉴设置子模块最大偏差的思想[28]所提出的电容电压分层控制法。分层控制法最多能降低一半的复杂度和降低接近一半频率,但是电容电压波动量也增大了近50%。文献[33]提出了一种禁忌搜索优化算法,通过桥臂电流方向、投入个数、子模块电压大小、子模块状态、器件开关频率等信息作为关键参数建立目标函数和约束条件,以禁忌搜索优化算法建立了状态决策优化模型。该算法另辟蹊径,与常规的排序算法的出发点不同,通过建立目标函数进行搜索达到均压目的,运算量大大降低。但是该算法的实现效果较难,且降频效果不明显,推广应用有一定难度。
文献[34]将用于载波移相技术的降频方法[14]改进后应用于NLM,适用于高电平MMC,最多可将开关频率降至2倍基频之下(82 Hz),大大降低开关损耗;但是算法的过程较为繁琐,均压效果很差。文献[35]提出一种适用于全桥MMC的无需排序的均压策略。该策略通过检测导通子模块数的变化以及判断各子模块的电容电压是否越界,来决定是否重新计算触发脉冲。该方法最多可以将开关频率降至72 Hz,排序效果优于文献[34]。文献[36]与文献[35]思想相似,其在导通子模块数变化时,找到电容电压最值子模块,然后交换脉冲信号。这种方法以较少的排序运算总量达到均压的目的,并且可以同时降低开关频率,最低可以降至68 Hz。文献[34-36]的方法都以不排序或少排序为优势来减少总的运算量,但是时间复杂度没有发生变化,这在硬件实现时仍不具有优势。此外,这3种方法实现过程繁琐,过于复杂,应用前景一般。
文献[37]提出了一种适用于FPGA的均压排序算法,根据导通的子模块数动态分组排序,尽量避免不必要的附加开关动作,能将时间复杂度降至传统排序算法的三分之一,开关频率降至300 Hz。值得尝试推广。文献[38]提出取整修正量移位算法,先将子模块进行分组,引入偏差量然后分组调制,不同的子模块组采用不同的取整修正量。均压效果能达到基本要求,但是具体的时间复杂度和开关频率有待进一步获取。
AB型算法从复杂度方面大多优于B型算法,AB型算法因其低复杂度和低开关频率的双重优势使其运用范围更为广泛,但阻碍AB型算法推广的原因之一是电容电压的一致性差于传统均压算法。

表1 3种类型均压算法评价Table 1 Evaluation for three types of voltage balancing ranking algorithms
评价均压排序算法主要指标应包括时间复杂度、开关频率、实现难度、电容电压总体波动系数和电容不平衡度等[32,39]。综上,不同类型的均压排序算法有其不同的特点,如表1所示,可以看出A型算法和AB型算法因优势更多而推广价值更大,但选择采用哪种排序均压算法应针对不同应用场景的需求具体分析。
3 几种典型算法均压效果对比
为了更好地说明均压效果的差异,本节取2种典型的A型算法[19,20]、典型的B型算法、典型的AB型算法与传统冒泡排序算法对比,对比它们的均压效果。在PSCAD中搭建401电平MMC双端系统[40],系统参数与文献[20]中3.1节表1一致。提取稳态时A相上桥臂部分子模块电容电压,如图2所示。质因子分解排序法、混合排序法和传统冒泡排序法的子模块电容电压波动幅值上下限都分别为1.8 kV,1.4 kV,幅值一致;三者的每个子模块的电容电压的一致性基本一样。这3种算法的时间复杂度分别为式T1,T2,T0,综合考虑这3种排序算法中混合排序法T2为最优[20]。
本节复现了文献[27]的仿真,测量子模块电容电压,如图3所示。各个子模块电容电压值分布分散,与图2相比,一致性差很多。经计算δ,ε[33]分别为15.38%,23.82%,都超过了极限波动系数15%,给系统可靠性带来威胁。
在PSCAD中搭建模型,测量双保持因子法[31]和传统排序法的子模块电容电压进行对比。
由图4看出,传统排序法电容电压幅值上下限为1.015 kV,0.99 kV,δ,ε[33]分别为2.5%和2.49%;双保持因子法电容电压幅值上下限为1.028 kV,0.98 kV,δ,ε分别为4.8%,4.78%;波动幅值大于传统排序法;该AB型算法的2项电容电压均衡指标接近传统方法上的2倍,每个子模块电容电压值分布较分散,一致性差于传统排序法。
综上,本节所复现的排序算法中,对比时间复杂度混合排序法为最低,均压效果最好;文献[27]算法开关频率最低,但子模块波动超过了极限;双保持因子法既降低时间复杂度又降低了开关频率,电容电压波动差于冒泡排序但符合要求。

图2 A型排序算法电容电压Fig.2 Capacitors voltage for sorting algorithms of type A

图3 B型排序算法电容电压Fig.3 Capacitors voltage for sorting algorithm of type B

图4 AB型排序算法电容电压Fig.4 Capacitors voltage for sorting algorithms of type AB
4 实时仿真均压排序算法
实时仿真是MMC工程投运之前的必经环节[41],实时仿真对MMC排序算法的要求更高[42],尤其是时间复杂度和算法实现难度(可靠性)。MMC实时仿真中的排序算法除了对算法本身改进外,还可以在硬件实现的过程进行优化改进,如并行处理[43]和分布式处理[44]等。因FPGA具有并行处理的特点,现有的高压大容量MMC电容电压排序算法大都采用FPGA来实现,主要的排序算法有归并排序、堆排序、快速排序和高速巴切奇偶排序等[23]。
文献[20]提出的混合排序算法时间复杂度尽管已经相对传统算法大为降低(为N log2N),但要应用于FPGA实现,复杂度仍然较高。文献[23]提出的基于桶排序分组的均压算法,每个FPGA时钟的排序复杂度仅为2N,很适合应用于高压大容量MMC系统的均压。文献[37]通过改进载波移相调制,将子模块动态分组,结合FPGA并行的特点,提出了一种适用于FPGA的均压算法。文献[43]在此基础上,引入并行全比较排序算法和设置子模块最大偏差,将算法进一步优化。排序运算可在4个FPGA时钟实现,且运算时间不会随子模块增加而增加。文献[44]将子模块均压控制分至多个控制器进行控制,这种分布式处理方式适合实时仿真。另外一种可应用于实时仿真的是排序预测算法或MMC预测控制,通过建立预测模型减少排序计算量,该类算法对多端MMC系统[45]和未来直流电网[46]的实时仿真的深入研究有一定借鉴意义。
综上,FPGA对排序算法的要求为:低时间复杂度,算法实现简单,以及算法能够利用FPGA并行处理。
5 结语
MMC的电容电压均衡控制策略是柔性直流输电应用的关键技术与难点。本文通过研究国内外主要的MMC排序均压算法,对其进行整理分类,对MMC均压排序算法评价指标进行了探讨,对部分算法进行了比较,得到以下结论:
(1)A型(降复杂度)均压算法其中的部分低复杂度算法可应用于实时仿真进而推广,可以进一步研究;B型(降频)算法在换流器要求特定的开关频率时可以应用,研究已较为充分;AB型算法用途较广,将成为未来的研究热点。
(2)MMC均压算法的评价指标应主要包括:时间复杂度、电容总体波动系数、电容不平衡度、器件开关频率和算法实现难度等。
(3)实时仿真排序算法在(2)中评价指标更注重时间复杂度和算法实现难度,以及结合FPGA的并行处理特点来改进,是未来MMC均压排序算法的研究方向。
[1]汤广福,庞 辉,贺之渊.先进交直流输电技术在中国的发展与应用[J].中国电机工程学报,2016,36(7):1760-1771.
TANGGuangfu,PANGHui,HEZhiyuan.R&Dand application of advanced power transmission technology in China[J].Proceedings of the CSEE,2016,36(7):1760-1771.
[2]XU J,ZHAO C,XIONG Y,et al.Optimal design of MMC levels for electromagnetic transient studies of MMC-HVDC[J]. IEEE Transactions on Power Delivery,2016,31(4):1663-1672.
[3]许建中,李承昱,熊 岩,等.模块化多电平换流器高效建模方法研究综述[J].中国电机工程学报,2015,35(13):3381-3392.
XU Jianzhong,LI Chengyu,XIONG Yan,et al.A review of effi⁃cient modeling methods for modular multilevel converters[J]. Proceedings of the CSEE,2015,35(13):3381-3392.
[4]刘钟淇,宋 强,刘文华.基于模块化多电平变流器的轻型直流输电系统[J].电力系统自动化,2010,34(2):53-58.
LIU Zhongqi,SONG Qiang,LIU Wenhua.VSC-HVDC system based on modular multilevel converters[J].Automation of Elec⁃tric Power System,2010,34(2):53-58.
[5]熊 岩,许建中,赵成勇,等.考虑相对误差和计算复杂度的MMC最佳等效仿真电平数的确定方法[J].中国电机工程学报,2016,36(7):1859-1867.
XIONG Yan,XU Jianzhong,ZHAO Chengyong,et al.Optimal selection of the equivalent MMC simulation scale considering the relative error and the computation complexity[J].Proceedings of the CSEE,2016,36(7):1859-1867.
[6]辛业春,王朝斌,李国庆,等.模块化多电平换流器子模块电容电压平衡改进控制方法[J].电网技术,2014,38(5):1291-1296.
XIN Yechun,WANG Chaobin,LI Guoqing,et al.An improved balance control for sub⁃module capacitor voltage of modular multilevel converter[J].Power System Technology,2014,38(5):1291-1296.
[7]SAEEDIFARD M,IRAVANI R.Dynamic performance of a mod⁃ular multilevel back⁃to⁃back HVDC system[J].IEEE Transac⁃tions on Power Delivery,2010,25(4):2903-2912.
[8]丁冠军,丁 明,汤广福,等.新型多电平VSC子模块电容参数与均压策略[J].中国电机工程学报,2009,29(30):1-6.
DING Guanjun,TANG Guangfu,DING Ming,et al.Sub⁃module capacitance parameter and voltage balancing scheme of a new multilevel VSC modular[J].Proceedings of the CSEE,2009,29(36):1-6.
[9]LESNICAR A,MARQUARDT R.An innovative modular multi⁃level converter topology suitable for a wide power range[C]∥Power Tech Conference Proceedings,2003 IEEE,Bologna,2003:3-6.
[10]赵成勇.柔性直流输电建模和仿真技术[M].北京:中国电力出版社,2014:78-87.
ZHAO Chengyong.Modeling and simulation technology on VSC-HVDC[M].Beijing:China Electric Power Press,2014:78-87.
[11]胡兆庆,董云龙,田 杰,等.基于模块化多电平换流器结构的柔性直流控制策略[J].江苏电机工程,2013,32(1):5-12.
HU Zhaoqing,DONG Yunlong,TIAN Jie,et al.Control strategy research of VSC-HVDC based on modular multilevel converter[J].Jiangsu Electrical Engineering,2013,32(1):5-12.
[12]FRANQUELO L G,RODRIGUSZ J,LEON J,et al.The age of multilevel converters arrives[J].Industrial Electronics Maga⁃zine,IEEE,2008,2(2):28-39.
[13]HAGIWARA M,AKAGI H.Control and Experiment of Pulse⁃width⁃Modulated Modular Multilevel Converters[J].IEEE Transactions on Power Electronics,2009,24(7):1737-1746.
[14]TU QR,XUZ,XUL.Reducedswitching⁃frequency modulation and circulating current suppression for modular multilevel converters[J].IEEETransactionsonPower Delivery,2011,36(3):2009-2017.
[15]赵 昕,赵成勇,李广凯,等.采用载波移相技术的模块化多电平换流器电容电压平衡控制[J].中国电机工程学报,2011,31(21):48-55.
ZHAO Xin,ZHAO Chengyong,LI Guangkai,et al.Sub⁃module capacitance voltage balancing of modular multilevel converter based oncarrierphaseshiftedSPWMtechnique[J]. Proceedings of the CSEE,2011,31(21):48-55.
[16]DENG Fujin,CHEN Zhe.A control method for voltage balan⁃cing in modular multilevel converters[J].IEEE Transactions on Power Electronics,2013,29(1):66-76.
[17]管敏渊,徐 政,潘伟勇,等.最近电平逼近调制的基波谐波特性解析计算[J].高电压技术,2010,36(5):1127-1132.
GUAN Minyuan,XU Zheng,PAN Weiyong,et al.Analytical calculation of fundamental wave and harmonic characteristics for nearest level modulation[J].High Voltage Engineering,2010,36(5):1127-1132.
[18]TU Qingrui,XU Zheng.Impact of sampling frequency on har⁃monic distortion for modular multilevel converter[J].IEEE Transactions on Power Delivery,2011,26(1):298-306.
[19]彭茂兰,赵成勇,刘兴华,等.采用质因子分解法的模块化多电平换流器电容电压平衡优化算法[J].中国电机工程学报,2014,34(33):5846-5853.
PENG Maolan,ZHAO Chengyong,LIU Xinghua,et al.An opti⁃mized capacitor voltage balancing control algorithm for modular multilevel converter employing prime factorization method[J]. Proceedings of the CSEE,2014,34(33):5846-5853.
[20]何智鹏,许建中,苑 宾,等.采用质因子分解法与希尔排序算法的MMC电容均压策略[J].中国电机工程学报,2015,35(12):2980-2988.
HE Zhipeng,XU Jianzhong,YUAN bin,et al.A capacitor voltage balancing strategy adopting prime factorization method and shell sorting algorithm for modular multilevel converter[J].Proceedings of the CSEE,2015,35(12):2980-2988.
[21]XU J,ZHAO C,et al.Enhanced high⁃speed electromagnetic transient simulation of MMC-MTDC grid[J].Electrical Power and Energy Systems,2016,3:7-14.
[22]罗永捷,李子欣,李耀华,等.一种模块化多电平换流器分布式均压控制策略[J].电源学报,2015(6):77-83.
LUO Yongjie,LI Zixin,LI Yaohua,et al.A distributed control method for voltage balancing in modular multilevel con⁃verters[J].Journal of Power Supply,2015(6):77-83.
[23]俎立峰,胡四全,吉攀攀,等.一种适用于高电压等级的MMC子模块均压算法[J].中国电力,2016(2):118-121.
ZU Lifeng,HU Siquan,JI Panpan,et al.A high voltage level MMC sub module equalization algorithm[J].Electric Power,2016(2):118-121.
[24]QINJ,SAEEDIFARDM.Reducedswitching⁃frequency voltage⁃balancing strategies for modular multilevel HVDC con⁃verters[J].IEEE Transactions on Power Delivery,2013,28(4):2403-2410.
[25]管敏渊,徐 政.MMC型VSC-HVDC系统电容电压的优化平衡控制[J].中国电机工程学报,2011,31(12):9-14.
GUANMinyuan,XUZheng.Optimizedcapacitorvoltage balancing control for modular multilevel converter based VSCHVDC system[J].Proceedings of the CSEE,2011,31(12):9-14.
[26]DARUS R,POU J,KONSTANTINOU G,et al.A modified voltage balancing sorting algorithm for the modular multilevel converter:Evaluation for staircase and phase⁃disposition PWM[C]∥Applied Power Electronics Conference and Exposition(APEC),IEEE 2014 Twenty⁃Ninth Annual,2014:255-260.
[27]郭裕群,赵成勇,许建中,等.模块化多电平换流器子模块平均开关频率的精确控制方法[J].电力系统自动化,2016,40(19):94-100.
GUO Yuqun,ZHAOChengyong,XUJianzhong,etal. Precision control method of average sub⁃module switching fre⁃quency for modular multilevel converters[J].Automation of Electric Power System,2016,40(19):94-100.
[28]屠卿瑞,徐 政,郑 翔,等.一种优化的模块化多电平换流器电压均衡控制方法[J].电工技术学报.2011,26(5):15-20.
TU Qingrui,XU Zheng,ZHENG Xiang,et al.An optimized voltage balancing method for modular multilevel converter[J]. Transactions of China Electro technical Society,2011,26(5):15-20.
[29]DENG F,CHEN Z.Voltage⁃balancing method for modular multilevel converters switched at grid frequency[J].IEEE Transactions on Industrial Electronics,2015,62(5):2835-2847.
[30]ILVES K,ANTONOPOULOS A,NORRGA S,et al.A new modulation methodforthemodularmultilevelconverter allowing fundamental switching frequency[J].IEEE Transac⁃tions on Power Electronics,2012,27(8):3482-3494.
[31]陆 翌,王朝亮,彭茂兰,等.一种模块化多电平换流器的子模块优化均压方法[J].电力系统自动化,2014,38(3):52-58.
LU Yi,WANG Chaoliang,PENG Maolan,et al.An optimized methodforbalancingsub⁃modulevoltagesinmodular multilevel converters[J].Automation of ElectricPower System,2014,38(3):52-58.
[32]林周宏,刘崇茹,李海峰,等.模块化多电平换流器的子模块电容电压分层均压控制法[J].电力系统自动化,2015,39(7):175-181.
LIN Zhouhong,LIU Chongru,LI Haifeng,et al.A stratified voltage balancing control method of sun⁃module capacitor voltage for modular multilevel converter[J].Automation of Electric Power System,2015,39(7):175-181.
[33]姜喜瑞,贺之渊,汤广福,等.基于禁忌搜索优化算法的高压大容量柔性直流输电子模块电容电压平衡算法[J].中国电机工程学报,2013,33(21):71-80,195.
JIANG Xirui,HE Zhiyuan,TANG Guangfu,et al.A capacitor voltage balancingcontrolstrategyforhigh⁃voltagelarge⁃capacity VSC-HVDC systems based on tabu search hard opti⁃mization algorithm[J].Proceedings of the CSEE,2013,33(21):71-80,195.
[34]许 烽,徐 政,张哲任,等.基于降损调制技术的全桥MMC电容电压无需排序均衡控制[J].电网技术,2013,37(2):3347-3355.
XU Feng,XU Zheng,ZHANG Zheren,et al.Reduced loss modulation basedcapacitorvoltagenon⁃sortingbalancing control for full⁃bridge MMC[J].Power System Technology,2013,37(2):3347-3355.
[35]喻 锋,王西田,林卫星,等.一种快速的模块化多电平换流器电压均衡控制策略[J].中国电机工程学报,2015,35(4):929-934.
YU Feng,WANG Xitian,LIN Weixing,et al.A fast voltage balancing control method for modular multilevel converter[J]. Proceedings of the CSEE,2015,35(4):929-934.
[36]喻 锋,王西田.基于冒泡原理的模块化多电平换流器快速电压均衡控制策略[J].电力自动化设备,2015,35(9):81-86.
YU Feng,WANG Xitian.Fast voltage balancing control based on bubbling principle for modular multilevel converter[J]. Electric Power Automation Equipment,2015,35(9):81-86.
[37]常 非,杨晓峰,贾海林,等.适用于现场可编程门阵列的MMC电容电压平衡控制方法[J].电网技术,2015,39(5):1246-1253.
CHANG Fei,YANG Xiaofeng,JIA Hailin,et al.A capacitor voltage balance control algorithm for modular multilevel con⁃verter suitable to field programmable gate array[J].Power System Technology,2015,39(5):1246-1253.
[38]郭高朋,姚良忠,温家良.模块化多电平变流器的子模块分组调制及均压控制[J].中国电机工程学报,2016,36(1):145-153.
GUO Gaopeng,YAO Liangzhong,WEN Jialiang.The grouping modulation and voltage balance control of the sub⁃modules in modular multilevel converter[J].Proceedings of the CSEE,2016,36(1):145-153.
[39]黄守道,廖 武,高 剑,等.基于改进均压算法的模块化多电平变流器开关频率分析[J].电工技术学报,2016,31(13):36-45.
HUANG Shoudao,LIAO Wu,GAO Jian,et al.Switching fre⁃quency analysis of modular multilevel converter based on the improvedcapacitorvoltagebalancingalgorithm[J]. Transactions of China electro⁃technical Society.2016,31(13):36-45.
[40]GNANARATHNA U N,GOLE A M,JAYASINGHE R P.Effi⁃cient modeling of modular multilevel HVDC converters(MMC)on electromagnetic transient simulation programs[J].IEEE Transactions on Power Delivery,2011,26(1):316-324.
[41]熊 岩,赵成勇,刘启建,等.模块化多电平换流器实时仿真建模与硬件在环实验[J].电力系统自动化,2016,40(21):84-89.
XIONG Yan,ZHAO Chengyong,LIU Qijian,et al.Modeling of MMC real time simulation and hardware in the loop experi⁃ment[J].Automation of Electric Power System,2016,40(21):84-89.
[42]KORN A J,WINKELNKEMPER M,STEIMER P,et al.Ca⁃pacitor voltage balancing in modular multilevel converters[C]. IET Power Electronics Machines and Drives International Con⁃ference,Bristol,2012:1-5.
[43]常 非,杨中平,陈 俊,等.模块化多电平换流器电容电压平衡并行排序方法[J].高电压技术,2016,42(10):3166-3171.
CHANG Fei,YANG Zhongping,CHEN Jun,et al.Parallel sorting method for capacitor voltage balancing of MMC[J]. High Voltage Engineering,2016,42(10):3166-3171.
[44]李建国,杨文博,宋 强,等.模块化多电平换流器电容电压的分布式均衡控制方法[J].电力系统自动化,2016,40(17):197-203.
LI Jianguo,YANG Wenbo,SONG Qiang,et al.Distributed balancing control strategy of capacitor voltage for modular mul⁃tilevel converter[J].Automation of Electric Power System,2016,40(17):197-203.
[45]李 岩,龚雁峰,姜 斌.一种基于方向行波的多端VSCHVDC系统保护策略[J].电力工程技术,2017,36(1):71-74.
LI Yan,GONG Yanfeng,JIANG Bin.A protection scheme for multiterminal VSC-HVDC system based on direction traveling waves[J].Electric Power Engineering Technology,2017,36(1):71-74.
[46]徐 政,张哲任,刘高任.柔性直流输电网的电压控制原理研究[J].电力工程技术,2017,36(1):54-59.
XU Zheng,ZHANG Zheren,LIU Gaoren.Research on voltage control principle of flexible DC transmission power grid[J]. Electric Power Engineering Technology,2017,36(1):54-59.
A Review of Ranking Algorithms for MMC Capacitor Voltages Balancing
XIONG Yan,ZHAO Chengyong,XU Jianzhong
(State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources
(North China Electric Power University),Beijing 102206,China)
Modular multilevel converter(MMC)system with high voltage and capacity has been widely applied among the VSC-HVDC projects in the world.In MMC application,capacitor voltage balancing ranking algorithms became a hot topic.This paper respectively focused on voltage balancing ranking algorithms suited for high⁃level MMC to summarize the state of the art literatures of this field methodically,and then to explore the cutting⁃edge research to show the core issues and concerns in the area.The sorting methods are clarified according to the purposes of reducing time complexity or switching frequency and the collective main ideas of them are extracted.This paper also explored the evaluating indicators for MMC ranking algorithms.By simulations,the capacitor voltage balancing effects of three algorithms with different complexities are compared.The switching frequencies of algorithms with maintaining factor are measured.In the end of this paper,the development direction of ranking algorithms in FPGA(field program gate array)for MMC real⁃time simulation is discussed.
modular multilevel converter;ranking algorithm;group sorting;time complexity;switching frequency;real⁃time simulation
TM73
:A
:2096-3203(2017)02-0001-08

熊 岩
熊 岩(1991—),男,江西宜春人,硕士研究生,研究方向为柔性直流输电仿真建模与实时化;
赵成勇(1964—),男,浙江丽水人,教授,博士生导师,研究方向为高压直流输电;
许建中(1987—),男,山西临汾人,博士,讲师,研究方向为直流输电与FACTS技术。
(编辑 刘晓燕)
2016-11-21;
2017-01-05
中央高校基本科研业务费专项资金资助(2016MS07),国家自然科学基金项目(51607065)。
