地震应急物资需求预测的模糊案例推理技术*

郭继东，杨月巧

(防灾科技学院 经济管理系， 河北 廊坊 065201)

0　引言

在当前生产力发展水平条件下，地震仍难以预测，其发生常常具有高度的不确定性，也是难以避免的。地震造成巨大的人员伤亡、财产损失和长久的生态破坏。按照危机管理的4R模式[1]开展防震减灾工作，已为各国政府、非政府组织及研究者们所接受。其中，地震的应急响应工作尤为重要，而对于应急响应，数量充足、结构合理、运转及时的应急物资储备及供应，更是灾后开展救灾响应工作的重中之重，这对于提升地震应急管理工作的效率和效果具有十分重大的意义，是后续应急救援、安置等工作得以顺利进展的基础和保障[2-3]，也是体现政府应急管理水平的重要方面。

地震应急物流的前提和基础，正是灾后对于地震应急物资的需求预测[4-5]。因为地震发生的小概率性和不确定性，导致震后物资需求也表现出极大的突发性、不确定性、高度时效性和弱经济性等特点[6]。地震的应急物资需求可从3个方面度量，分别是：应急物资的种类数量、时间成本及结构组合[7]。

需求预测的方法有很多，基本上可分为定性和定量2大类[8]。前者的代表诸如专家预测法，这也是目前我国在震后物资需求预测方面采用最多的1种方法，它以专家的经验判断为主；而后者的代表就包括时间序列预测法、预测模型法等，一些智能的决策支持系统中的智能化预测方法得到学者们的关注和应用[9]。专家预测法对专家的经验和判断力有较高要求，且不能轻易实现知识转移；定量化的方法对数据较为依赖，而对于震后信息通道中断、统计困难的情况，决策人只能根据寡信息进行迅速决策，在这样的背景下，基于案例推理法找到了用武之地[10]。利用案例数据库中不多的案例特性信息，将新生案例的特性与之进行相似性分析，利用已有案例的物资需求信息，辅以专家判断或关键因素模型，最后得到新生案例的应急物资需求预测，这显然是1种定性和定量结合的预测方法。

首先，介绍模糊集和隶属度的一些概念及公式；其次，探讨基于模糊案例推理技术的步骤和关键；最后，在实际案例中，基于震后信息稀缺的特征，利用模糊集合的概念来表征地震发生时的关键特征属性，并用模糊集合的测度贴近度度量新旧案例之间的相似性，得到已有案例库中与当前新发生案例最为相似的旧案例。

1　模糊集

模糊技术几乎渗透到了所有科学领域[11]。Kaufmann首先提出模糊变量[12]的概念，之后被Zadeh引用并发展[13]；Zadeh首先提出模糊集合的概念和可能性理论[14]，逐步建立模糊集的公理化体系[11]。

隶属函数的几何形态一般有三角形、梯形、S形等。在地震的特征表达方面，我们一般采用S形的隶属度函数，有时也采用梯形隶属度函数，形态如图1所示。

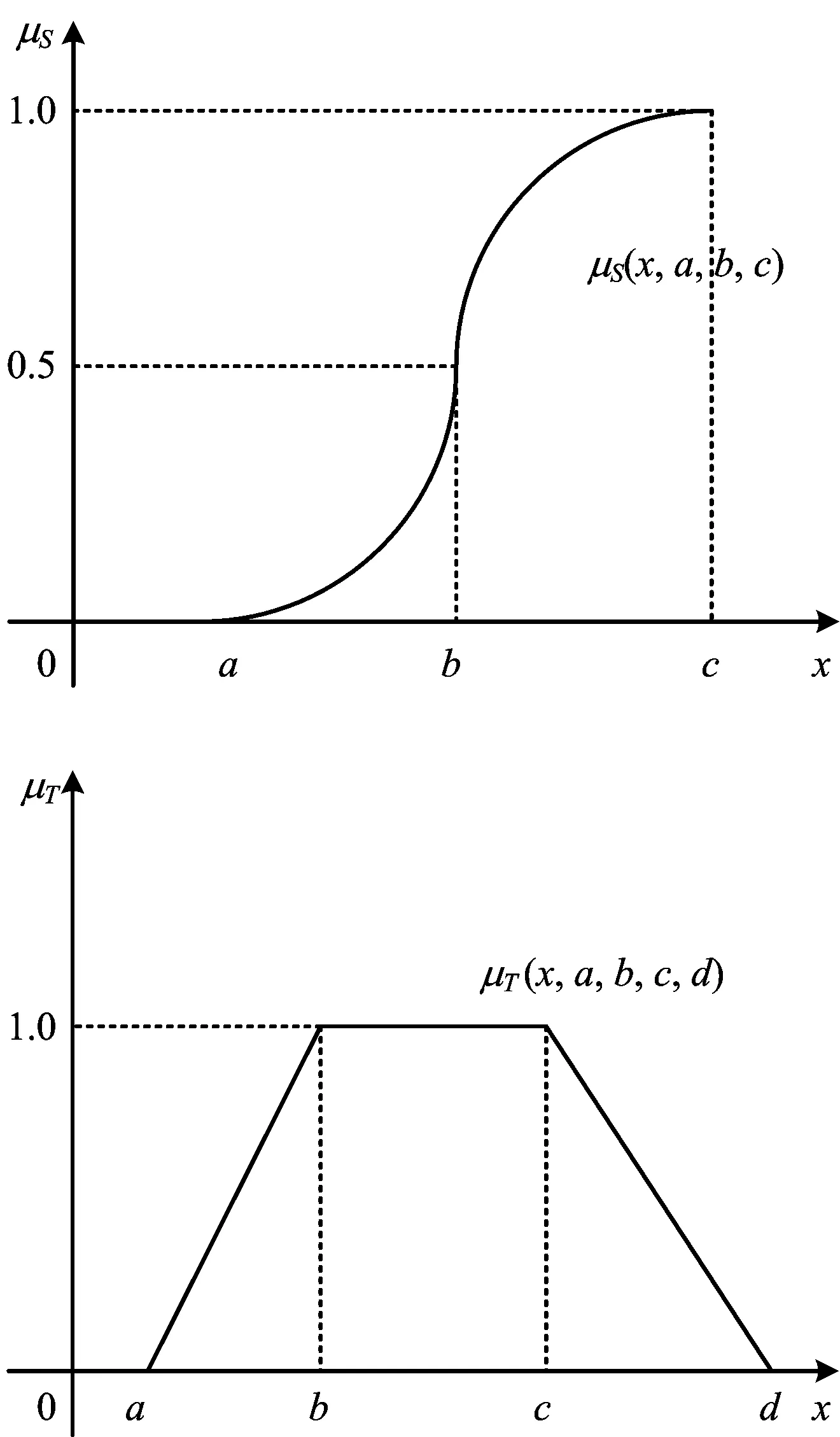
图1　S与梯形隶属度函数Fig.1　S-shaped and trapezoid membership functions

根据新发生地震的初步特征分析，就可以根据隶属度函数确定其对于该模糊集合的隶属度。在得到所有新生地震特征属性后，仍需要将其与案例库中所有已有的案例进行相似形判断。这里，引入1个衡量特征向量，即隶属度向量之间相似性判断计算方法—测度贴近度。为了介绍测度贴近度的计算，先介绍贴近度的定义。

2　基于模糊案例推理的地震应急物资需求估计

案例推理技术原理简单易懂，对应于现实中解决新问题的直觉思考模式，即对于新案例来讲，在可利用信息较少的情况下，只有求助于案例库中与之相似的旧案例。通过新旧案例之间问题特征的分析，选择与当前新案例较为相似的旧案例作为参考，之后再借鉴专家对新案例的理解和分析，帮助决策者作出最后决策。而模糊案例推理技术则是把模糊集合的概念引入到新旧案例特征属性的表达上，利用模糊算子计算案例之间的相似性。在实际应用中，模糊案例推理技术一般分为以下4步。

2.1　案例特征属性表达

假设案例库中有N个案例，每个案例有M个特征属性(依靠经验，在数据可获得性基础上提取)。第i个案例用Ci表示，第i个案例的第j个属性用fij表示，则可构造如下数据结构矩阵或称为特征属性矩阵。其中，行向量表示案例，列向量表示特征属性。

2.2　计算特征属性隶属度

根据经验，设置以上M个特征属性的模糊集合，并根据各个案例的特征属性值，计算案例属性对于模糊集合的隶属程度。得到特征属性隶属度矩阵F:

将新的案例用G表示，则其特征属性的隶属度向量为FG=[fG1，fG2，…，fGM]。

2.3　案例相似性分析

将新案例的特征属性隶属度向量，即FG，逐个与矩阵F中第1到第N个行向量，按照测度贴近度公式计算其相似度，并对计算得到的N个测度贴近度进行排序。与新案例的测度贴近度最大的旧案例提取出来，即为最佳参照案例。

2.4　确定应急物资需求量

应急专家根据新旧2个案例之间，在特征属性上存在的不同，以及新案例所体现出的一些新的特征或情况，并根据新案例救援中采用的方法体系和救援条件、救援标准的不同，最终确定应急物资的需求。

3　应用算例

新生地震案例以2014年8月3日发生在云南省昭通市鲁甸县的地震(简称鲁甸地震)为例。在已有的地震案例数据库中，储存邢台地震、唐山地震、丽江地震、汶川地震、芦山地震、玉树地震、定西地震以及普洱地震等8个以往地震案例的详细信息。

从案例库中，按照专家意见，同时参考已有研究中对地震破坏性关键因素的选用结果[8,17]，共计抽取8个方面的主要特征因素，包括：震级、震源深度、持续时间、破坏面积、发生时间、经济水平、人口密度、城镇化率。考虑各个因素的重要性及统计数据的完整性，在案例中设置如下特征属性集合：

从案例中提取每个案例的特征属性信息。发生时间采用梯形模糊函数，原因在于发生时间决定人员的在室率，而后者决定地震所造成的人员伤亡，进而决定物资需求多寡，采用梯形模糊函数可以很好地描述该特征。其他4个特征属性均采用标准S形隶属度函数，该函数是经过正弦函数改变频率和坐标系内平移得到的。以震级为例，4.5级以下的地震一般不会造成破坏；在4.5级到8级之间，破坏程度急速上升；8级及以上级别地震我国还没有相关案例，一般认为破坏达到最大。正弦函数可以描述地震破坏力随震级快速上升的情形，根据上述隶属函数和案例中特征属性信息，可以计算得到所有新旧案例对于模糊集合的隶属度，参数a，b，c，d根据经验确定，如表1所示。

表1　地震特征属性的隶属函数中参数设定

其中地震发生时间点的模糊数形式为非对称的梯形，为了简化该梯形模糊数，以中午12点为计时0点，并以24 h为1个周期。所有新旧案例的特征属性信息如表2所示。

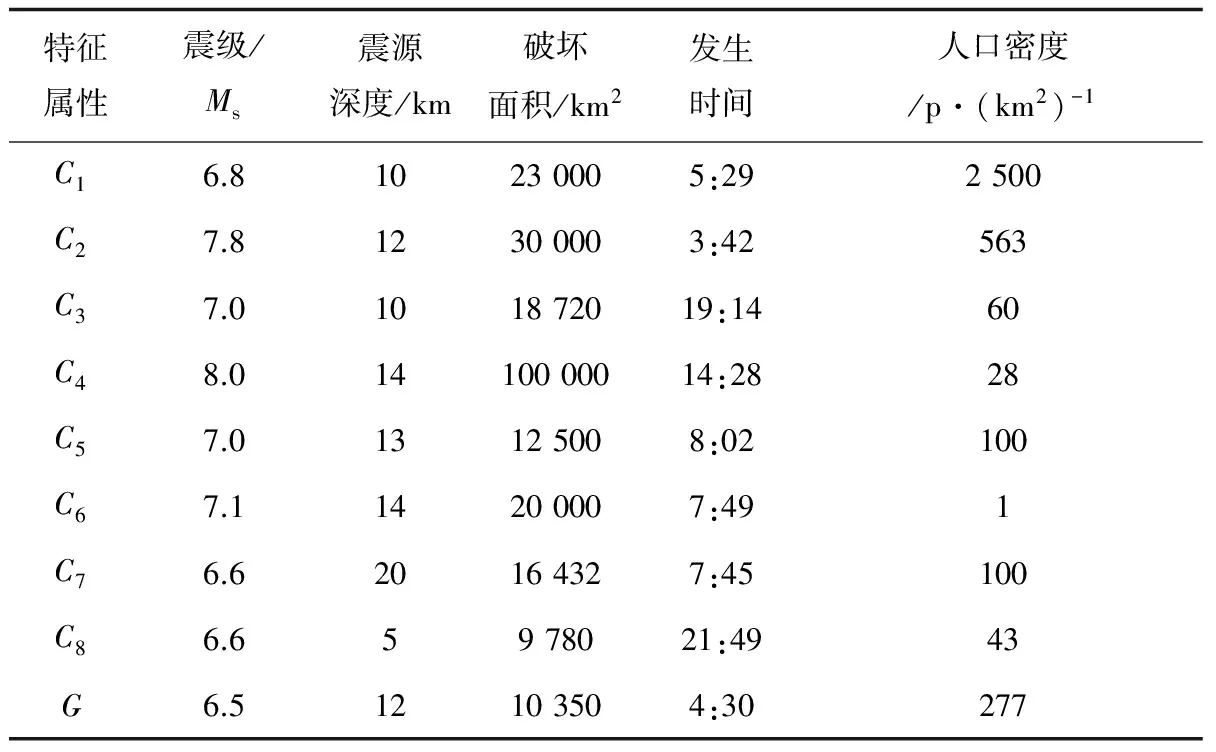
表2　新旧案例的地震特征属性值

将表2中的各个案例的特征属性带入到S形和梯形隶属度函数中，得到所有案例的特征属性隶属度矩阵，如表3所示。

表3　标准化后新旧案例的模糊特征属性值

利用层次分析法的判断矩阵方法来计算特征属性的相对重要性和权重，具体过程限于篇幅省略，直接给出权重向量，并根据模糊集贴近度公式，依次计算新旧案例之间的相似程度，如下：

w=[w1,w2,…,w5]=[0.610 5,0.071 2,0.203 2,0.041 2,0.073 9]；N(G，C)=[0.86,0.80,0.81,0.69,0.83,0.73,0.88,0.80]

可见，新案例(鲁甸地震)，与案例库中的第7个案例(定西地震)相似程度最高，如果在保障水平、救援技术水平等因素不变的情况下，可以参照定西地震救援物资的数量、质量及结构需求作出应急物资后勤运送配给安排。

4　结论

1)在地震发生后，根据能够获取的有限信息，需要决策者迅速做出物资采购、运送、配给等系列应急救援计划，而震后初步物资需求预测是后续这些关键决策的基础，模糊案例推理技术可以在有限信息下提供辅助决策。

2)采取模糊集合与基于案例分析相结合的技术，把地震的一些关键特征属性进行模糊化处理；把最新案例与案例库中已有案例，对于模糊集合的隶属程度进行估算，并在得到特征属性权重的基础上，计算新旧案例之间基于测度贴近度的相似性。以鲁甸地震为例进行物资需求分析比对，证明技术可行。

3)由于没有完全相同的地震个案，故可在相似案例物资需求信息的基础上，邀请专家对新案例中的一些新特点进行总结，进而对新个案中的物资需求信息进行修正。

[1]罗伯特·希斯.危机管理[M]. 北京:中信出版社, 2001:89-94.

[2]王成敏, 孔昭君, 杨晓珂. 基于需求分析的应急资源结构框架研究[J]. 中国人口·资源与环境, 2010, 20(1):44-49.

WANG Chengmin，KONG Zhaojun，YANG Xiaoke.Structural framework of emergency resources based on demands analysis[J]. China Population Resources and Environment, 2010,20(1):44-49.

[3]周进军, 李洪泉, 邓云峰,等. 地震灾害综合应急能力评估研究[J]. 中国安全生产科学技术, 2009, 5(3):56-60.

ZHOU Jinjun，LI Hongquan，DENG Yunfeng，et. al. Research on assessment of comprehensive emergency capacity for earthquake disaster[J]. Journal of Safety Science and Technology, 2009, 5(3):56-60.

[4]郑斌, 马祖军, 李双琳. 基于双层规划的震后初期应急物流系统优化[J]. 系统工程学报, 2014, 29(1):113-125.

ZHENG Bin，MA Zujun，LI Shuanglin. Integrated optimization of emergency logistics systems for post-earthquake initial stage based on bi-level programming[J].Journal of Systems Engineering, 2014,29(1):113-125.

[5]姜云昭, 朱万红, 邱国庆,等. 地震次生灾害影响条件下人员疏散问题的研究[J]. 中国安全生产科学技术, 2008, 4(1):38-41.

JIANG Yunzhao，ZHU Wanhong，QIU Guoqing，et. al.Study of evacuation under the condition of the seismic secondary disasters[J].Journal of Safety Science and Technology,2008,(1):38-41.

[6]Tufekci S, Wallace W A. The emerging area of emergency management and engineering[J]. IEEE Transactions on Engineering Management, 1998, 45(2):103-105.

[7]张永领. 基于模糊聚类的应急物资分类储备研究[J]. 灾害学, 2012, 27(1):130-134.

ZHANG Yongling. Research on classified reserve of emergency materials based on fuzzy clustering analysis[J]. Journal of Catastrophology, 2012,27(1):130-134.

[8]傅志妍, 陈坚. 灾害应急物资需求预测模型研究[J]. 物流科技, 2009, 32(10):11-13.

FU Zhiyan，CHEN Jian.Research on emergency material demand forecast model in disaster[J]. Logistics Science and Technology, 2009,32(10):11-13.

[9]王丰,姜玉宏,王进.应急物流[M]. 北京: 中国物资出版社, 2007:23-27.

[10]Derere M L. Case-based reasoning: Diagnosis of faults in complex systems through reuse of experience[A]//International Test Conference 2000[C], Proceedings, 2000: 27-34.

[11]刘宝碇，彭锦．不确定理论教程[M]．北京：清华大学出版社，2005：1-2．

[12]Kaufmann A. Introduction to the theory of fuzzy subsets[M]// Introduction to the theory of games. Физматгиз, 1977:1734-1734.

[13]Zadeh L A. The concept of a linguistic variable and its aplication to approximate reasoning[J]. Information Sciences, 1975, 8(3):199-249.

[14]Zadeh L A. Fuzzy sets[J]. Information & Control, 1965, 8(3):338-353.

[15]吴望名，等. 应用模糊集方法[M]. 北京师范大学出版社, 1985.

[16]顾凤岐, 赵连盛. 测度贴近度及其集值统计估值[A]// 中国系统工程学会96模糊理论与应用国际会议年会[C]. 1996:153-157.

[17]晁颖, 王庆荣. 基于模糊粗糙集案例推理的应急物资需求预测[J]. 交通科技与经济, 2015(5):1-4.

CHAO Ying，WANG Qingrong.Forecast of emergency material demand based on fuzzy rough sets and CBR[J].Technology & Economy in Areas of Communications,2015(5):1-4.