基于STSNN聚类算法的用沙坝矿微震事件活动特征研究*
2017-04-14李夕兵刘志祥董陇军周勇勇陈光辉
刘 栋,李夕兵,刘志祥,董陇军,周勇勇,陈光辉
(中南大学 资源与安全工程学院,湖南 长沙 410083)
0 引言
采矿活动向深部发展,破坏了深部的原岩应力,由此引起的地质灾害状况频发,微震监测技术是目前监测灾害的有效手段[1-2]。近几年,微震监测技术已经在台站布网优化[3-4]、P波[5-6]、S波拾取[7]、微震定位[8-9]及微震爆破事件识别[10]等方面有了较大的进展,并取得了一系列重要的研究成果。为了掌握岩体破坏的规律,对微震事件的聚集特征及活动规律研究显得尤为重要。在此方面,国内外学者做了许多创新性的研究,例如吴爱祥[11]等利用最短距离聚类法对某矿山微地震活动的时空分布进行了分析,识别了井下微震活动聚集区域;谢和平[12]等采用分形理论研究微震活动的时空分布,发现分形维数在一定程度上反映了微震活动的变化状态;Martin[13]利用空间聚类方法对微震事件进行聚类分析并解释了微震活动规律。纵观这些研究仍存在一定的不足:在划定微震活动的聚集区域时只考虑微震事件的空间分布特征,没有将时间特征考虑在内。对此,本文采用时空共享近邻聚类(STSNN)算法,将微震事件的时间空间特征相结合并展开聚类研究。2012年Liu等[14]将共享近邻概念引入时空聚类,提出STSNN聚类算法,该算法采用实体的有效近邻数目来定义其时空密度,更适于发现不同密度的时空簇,是时空聚类算法中较先进的聚类算法。
开磷用沙坝矿存在严重的潜在地压问题,于2013年安装使用IMS微震监测系统来监测井下灾害。本文以用沙坝矿为工程背景,以用沙坝矿IMS微震监测系统2014年收集到微震数据作为研究对象,通过P波、S波拾取后得到5 425个有效微震作为本文的数据集。采用STSNN算法并选择合适的参数对其进行聚类分析,计算其聚类有效性,并对最大类簇的微震事件活动规律进行探究,根据其变化规律发现产生较大事件的预警点。通过对微震事件活动规律的研究可为大事件的产生提供有效的预判信息,为保证矿山安全生产发挥重要的作用。
1 时空共享近邻聚类(STSNN算法)
1.1 基本定义
为了阐述时空近邻共享聚类算法,首先介绍几个重要的概念:
定义1时空事件:一个时空事件STi是具有空间坐标和确定的时间标志,表示为STi(Li,ti)。
定义2时空近邻:时空事件STi的时空近邻定义为以ΔD作为底面半径、2ΔT作为高的圆柱体,ΔT为时间窗口。
定义3时空密度:时空事件STi的时空密度定义为STi时空直接可达的事件数量。
定义4时空可达:假如时空事件数据集ST1,ST2,…STi,…STn,STn是一个时空核心,如果STi-1是从STi时空直接可达,那么ST1也可视为从STn时空可达,表示为STn→ST1。
定义5噪声:假设时空事件STi不是一个时空核心,在精确时空近邻内不存在时空核心,那么可将STi视为噪声。
定义6时空类簇:对于一个时空数据集STD,时空类簇STC是满足下列2个条件的非空集。
条件1:∀STi∈STD,STj∈STD:STi→STj
条件2:∀STi∈STD,STj∈STD:STi~STj
1.2 STSNN算法及参数选择
STSNN算法需要用户设置4个参数:k,kT,MinPts和ΔT,k是时空近邻的事件数量,kT是判别两个事件是否时空直接可达的阈值,MinPts用来识别时空核心,ΔT是定义时空近邻的时间窗口。基于上述定义,STSNN算法的执行可分为以下5个步骤:
Step1:对每个时空事件确定时空近邻k。
Step2:对每个时空事件搜索其时空共享近邻。
Step3:计算每个时空事件的时空密度以及进一步探测时空核心。
Step4:扩大时空类簇。选择一个时空核心并使用递归算法将所有时空可达和时空相连的事件增加到时空类簇。
Step5:识别噪声事件。
STSNN参数kT和MinPts通常设置为0.5k。另外2个参数,k和ΔT在本次研究中,ΔT初选值设定为[5,6],k的初选值[5,6,7…17,18,19],共有30种组合,为了方便后面表达,每一种组合的类别符合的如表1所示。
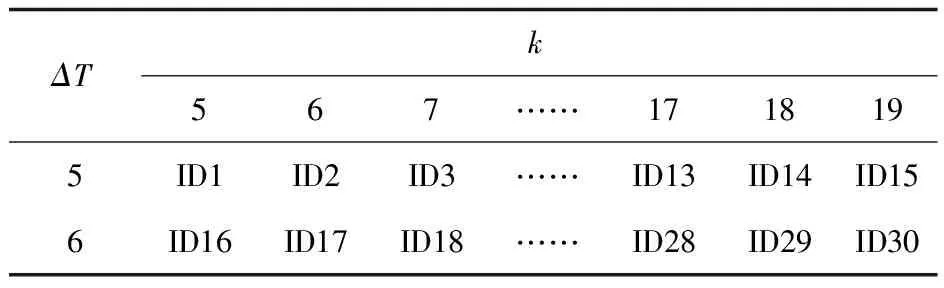
表1 30种组合的类别符号
2 聚类结果及有效性评价
分别利用STSNN算法对上述k和ΔT的30种组合进行聚类运算。当k和ΔT分别选择不同的值时,可以得到不同的聚类类簇,如图1所示,当ΔT一定k增大时,得到的类簇数量越来越少,而最大类簇事件数没有呈现规律性变化。图2表示不同类别的噪声率,除ID1(k=5,ΔT=5)和ID16(k=5,ΔT=6)外,其他类别的噪声率相对较低。
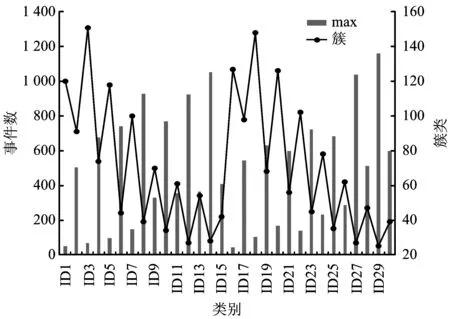
图1 不同类别的簇数及最大类簇事件数Fig.1 The number of clusters of different classes and the maximum number of cluster events

图2 不同类别的噪声率Fig.2 Noise rates of different classes
聚类有效性评价是为了确定对数据划分多少个类簇是最合适的。一个理想的聚类结果应该满足2方面要求[15]:(1)紧密性,即簇内实体应尽可能相似;(2)分离性,即不同簇间实体差异尽可能大。一个好的聚类结果应该同时满足紧密性与分离性。本文选择RMSSDT指数[16]和PBM指数[17]作为有效性评价指标。RMSSDT指数旨在度量实体间的离散程度,其值越小,则表示簇的均质性越好;PBM指数采用融合多个度量指标的策略来进行聚类结果的有效性度量,其值越大,表示聚类结果越可靠,如图3所示。
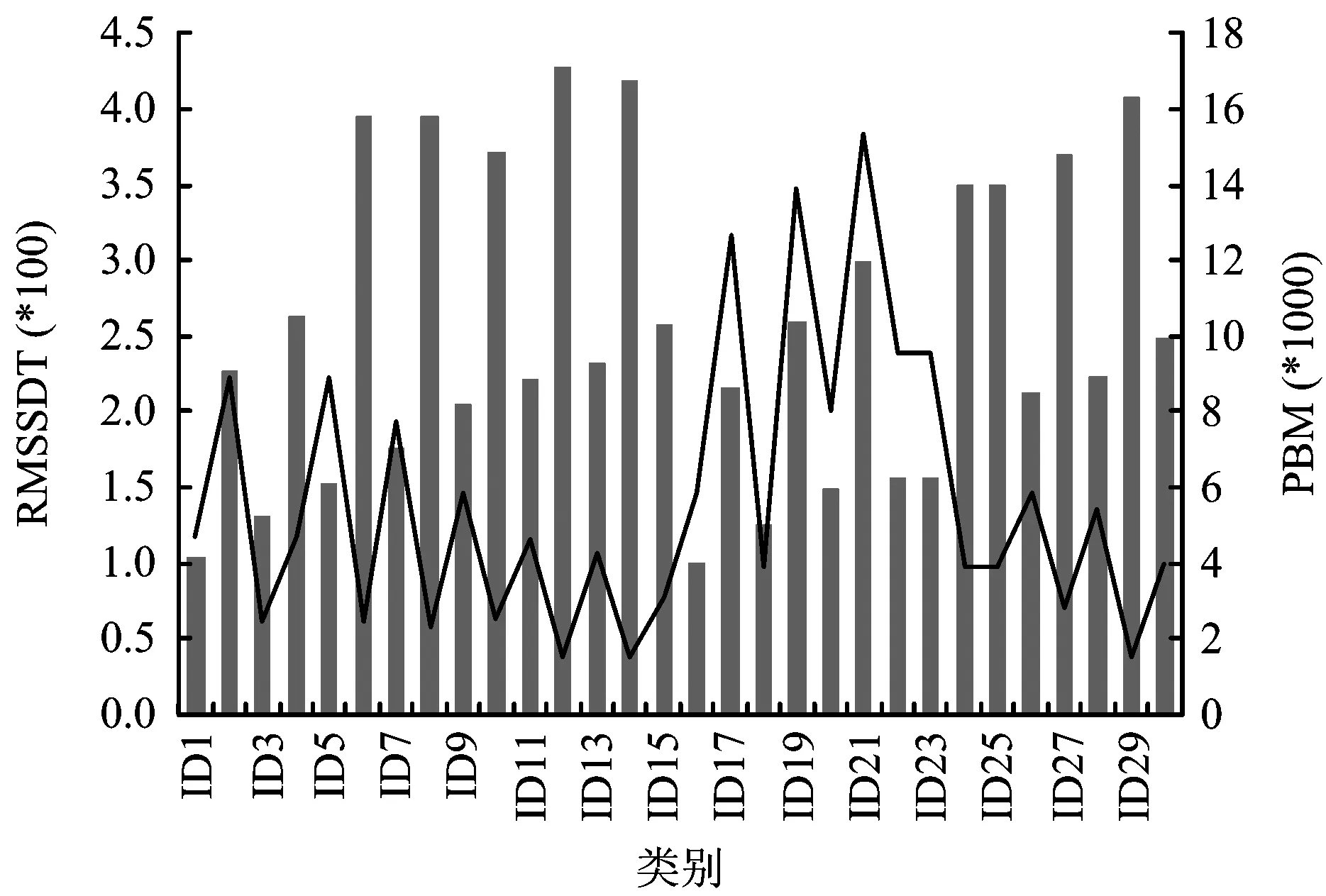
注:折线代表PBM;柱状图代表RMSSDT图3 聚类有效性评价结果Fig.3 Clustering effectiveness evaluation results
利用RMSSDT指数和PBM指数对每一类别的有效性进行评价,如图3所示单纯从PBM评价指标(折线)来看,ID17(k=6,ΔT=6)、ID19(k=8,ΔT=6)和ID21(k=10,ΔT=6)聚类效果较好,优势较明显,进而从RMSSDT指数(柱状图)来比较,ID17(k=6,ΔT=6)聚类结果最好,并且其噪声率不高,因此本文后续研究将利用ID17(k=6,ΔT=6)的聚类结果。该聚类共得到98个类簇,最大类簇的事件数为544,噪声率为24.8%。最大的5个类簇事件数分别为544,246,234,161和100。图4表示最大类簇在矿山中的主要聚集区域,从图中可以发现,该类簇主要集中在用沙坝矿的断层附近。
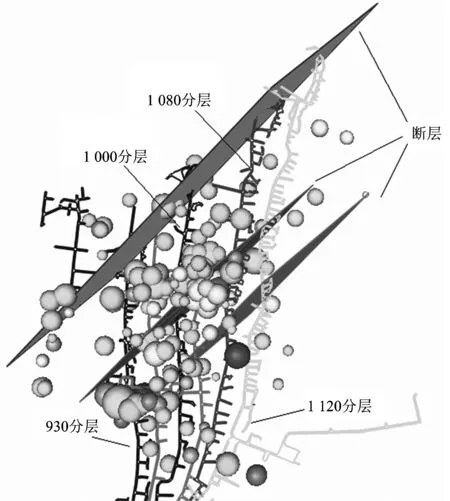
图4 最大类簇微震事件的主要聚集区域Fig.4 The events aggregation area of the biggest cluster group
3 微震事件活动特征
3.1 微震事件24 h分布

图5 微震事件24 h分布(m表示震级)Fig.5 The distribution of micro-seismic in 24 hours
图5表示该区域聚类事件的24 h分布图,微震事件主要发生在每天的11时到15时,大于0级的事件也主要发生在此时间段。用沙坝矿爆破时间主要集中在每天11时到14时。因此该区域的微震事件大部分分布在断层区域,受采矿活动诱发而产生。在非爆破时间,该区域的微震事件在时间分布上较为均匀,但偶尔也有震级大于-0.5级事件发生。
3.2 微震事件活动率与视体积
微震事件活动率反映了岩体内部微裂纹的扩展变化趋势,表现了微裂纹的产生和发展速度,微震事件的突变特征体现了岩体开挖导致围岩破坏的前兆信息。微震事件的视体积表征地震非弹性变形的体积与它释放的能量和体变势相关,累计视体积随时间变化曲线的斜率通常被认为是表示岩体应变速率的重要指标,曲线的斜率变化反映应变率的微小变化,岩体失稳变形的前兆是经历一段时间的加速变形过程。通过观察图6,可以按微震活动率分为3个阶段,AB阶段微震事件活动率降低,说明此阶段可能有大事件发生,能量得到释放;BC段微震活动率变化缓慢,说明此阶段岩体处于稳定状态,开始生成新的裂隙并呈稳定发展阶段;CD阶段为岩体内裂隙发展迅速,微震活动率增加,因此可能发生较大事件。累积视体积曲线在B点(5月3日附近)和C(5月10日附近)点明显上升,表明B,C点附近可能有破坏发生,导致岩体失稳。在CD段开始急剧上升,表明此阶段大量的微裂隙张开占据岩石空间导致岩石体积膨胀,视体积曲线突然增大的点可以作为发生大事件的前兆信息,因此在D(5月16日)点之后,很可能产生较大的破坏性事件。实际上在5月19日现场有一次震级为0.7级的微震事件发生。因此可以认为微震事件率急剧下降并且累积视体积曲线忽然上升是岩石发生破坏的预兆现象。
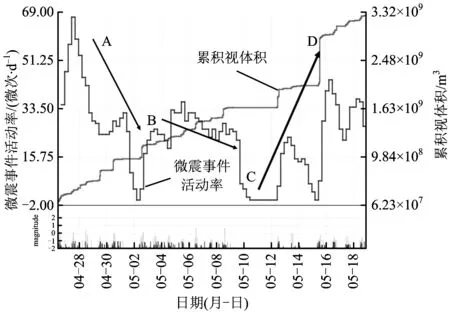
图6 微震活动率与累积视体积事件序列曲线Fig.6 Time series curve of cumulative apparent volume and event activity
3.3 施密特数与劲度系数
施密特数(Schmidt Number)是运动学黏度与扩散率之比,能测量震动岩石流变的时空复杂程度,也是反映岩石不稳定的参数,施密特数越低,稳定性越差。劲度系数(Stiffness Modulus)表征系统阻止地震变形和应力增加的能力。如图7所示施密特数曲线与劲度系数曲线保持相同的变化趋势,分别在5月2日、5月9和5月16日附近急剧上升然后迅速下降,降低程度几乎相同,施密特数处于较低水平时该区域的岩体稳定性较差,产生破坏的可能性比较大。在这3个时间,从劲度系数曲线可以看出,岩体阻止系统变形的能力也瞬间下降,进而也表明该区域在这3个时间较容易发生危险事故。而实际现场监测中,5月10日期间,发生了2次震级超过0.5级的微震事件,与5月9日附近施密特数劲度系数先升后降的预测基本对应。因此可以把施密特数和劲度系数先升后降的点作为大事件将要发生的预警信息。

图7 施密特数与劲度系数事件序列曲线Fig.7 Time series curve of Schmidt Number and Stiffness Modulus
4 结论
1)利用时空共享近邻(STSNN)聚类算法对用沙坝矿微震事件进行聚类分析,可以发现微震事件的时空聚集类簇,并对其聚类有效性进行分析,确定聚类参数选择的合理性。对微震事件聚类分析来确定所研究的区域,比人为划定的事件聚集区域更客观有效。
2)对聚类最大类簇的微震事件活动特征进行分析,通过24 h分布图可以发现用沙坝矿微震事件主要发生在每天的11时到15时,大于0级的时间也主要发生在此时间段,微震活动率急剧下降并且累积视体积曲线忽然上升、施密特数和劲度系数先升后降的点作为岩体失稳发生破坏性事件的预警点。
[1]李夕兵. 岩石动力学基础及应用[M]. 北京,科学出版社,2014.
[2]王春来,吴爱祥,刘晓晖.深井开采岩爆灾害微震监测预警及控制技术[M].北京,冶金工业出版社,2013.
[3]周勇勇,李夕兵,刘志祥,等. 高精度三维地下微震台网模糊优选方法[J]. 中国安全生产科学技术,2016, 12(7):82-86.
ZHOU Yongyong, LI Xibing, LIU Zhixiang, et al.A fuzzy optimum approach for high precision three-dimensional underground micro-seismic Network [J]. Journal of Safety Science and Technology, 2016, 12(7):82-86.
[4]张楚旋,李夕兵,董陇军,等. 微震监测传感器布设方案评价模型及应用[J]. 东北大学学报(自然科学版),2016(4):594-598,608.
ZHANG Chuxuan, LI Xibing, DONG Longjun, et al. Evaluation model of micro-seismic monitoring sensor layout scheme and its application[J].Journal of Northeastern University (Natural Science), 2016(4):594-598,608.
[5]LI X, SHANG X, WANG Z, et al. Identifying P-phase arrivals with noise: An improved Kurtosis method based on DWT and STA/LTA[J]. Journal of Applied Geophysics, 2016, 133: 50-61.
[6]LI X, SHANG X, Morales-Esteban A, et al. Identifying P phase arrival of weak events: the Akaike Information Criterion picking application based on the Empirical Mode Decomposition [J]. Computers & Geosciences, 2016.
[7]张楚旋,李夕兵,董陇军,等. 三函数四指标矿震信号S波到时拾取方法及应用[J]. 岩石力学与工程学报,2015(8):1650-1659.
ZHANG Chuxuan, LI Xibing, DONG Longjun, et al. A S-wave phase picking method with four indicators of three functions for micro-seismic signal in mines [J]. Chinese Journal of Rock Mechanics and Engineering, 2015(8):1650-1659.
[8]Linqi HUANG, Xibing LI, Longjun DONG, et al. Relocation method of micro-seismic source in deep mines [J]. Transactions of Nonferrous Metals Society of China, 2016(11):2988-2996.
[9]张飞, 刘德峰, 张衡,等. 基于IMS微震监测系统的微震事件定位精度分析[J]. 中国安全生产科学技术, 2013, 9(6):21-26.
ZHANG Fei, LIU Defeng, ZHANG Heng, et al. Location accuracy analysis of the seismic events based on the IMS micro-seismic monitoring system [J]. Journal of Safety Science and Technology, 2013, 9(6):21-26.
[10]GUOyan ZHAO, Ju MA, Long-jun DONG, et al. Classification of mine blasts and micro-seismic events using starting-up features in seismograms[J]. Transactions of Nonferrous Metals Society of China, 2015(10): 3410-3420.
[11]吴爱祥,武力聪,刘晓辉,等. 矿山微地震活动时空分布[J]. 北京科技大学学报,2012,34(6):609-613.
WU Aixiang,WU Licong,LIU Xiaohui,et al. Space-time distribution of micro-seismic activities in mines[J].Journal of University of Science and Technology Beijing,2012,34(6):609-613.
[12]谢和平,W. G. Pariseau. 岩爆的分形特征和机理 [J]. 岩石力学与工程学报,1993,12(1):28-37.
XIE Heping,Pariseau W G. Fractal character and mechanism of rockbursts [J]. Chinese Journal of Rock Mechanics and Engineering,1993,12(1): 28-37.
[13]Hudyma MR. Analysis and interpretation of clusters of seismic events [D]. University of Western Australia, Perth, Australia, 2008.
[14]Liu Q., Deng M., Bi J., Yang, W. A Novel Method for Discovering Spatio-temporal Clusters of Different Sizes, Shapes and Densities in the Presence of Noise [J].International Journal of Digital Earth,2012, 7(2): 138-257.
[15]Berry M, Linoff G. Data Mining Techniques: For Marking, Sales and Customer Support[M]. New York: Wiley, 1997.
[16]Halkidi M, Batistakis Y, Vazirgiannis M. Clustering algorithm and validity measures[A]. Proceedings of 13th International Conference on Scientific and Statistics Database Management[C]. 2001, 3-22.
[17]Pakhira M K, Bandyopadbyay A, Maulik U. Validity index for crisp and fuzzy clustering[J]. Pattern Recognition, 2004, 37(3):487-501.
