基于演化博弈的危化品安全监管情景推演研究*

王循庆,李勇建,孙晓羽

(1.山东工商学院 公共管理学院，山东 烟台 264005; 2.南开大学 商学院，天津 300071)

0　引言

随着国家经济快速发展和社会需求增长，各种危险化学品的使用量也越来越大，被广泛应用于各行各业。在危险化学品数量增长迅猛的同时，由于安全监管和生产过程存在漏洞，导致危险化学品事故灾害频发。如天津港“8.12”特别重大火灾爆炸事故造成165人遇难，8人失踪，798人受伤，截止2015年12月10日，已核定的直接损失高达68.66亿元，对社会生活和公共安全造成严重影响。这些事故灾害暴露出危险化学品管理存在安全意识淡薄、安全监管疏忽等问题，对危险化学品安全监管问题的研究具有重大现实意义。

危险化学品安全事故的发生与监管的漏洞、企业安全投入的不足有着直接或间接的关系[1-3]。从生产安全监管层面，MAKIN A M和WINDER C[4]讨论外部环境对企业安全生产的影响，提出加大外部政府监管力度能提高安全生产管制效果。从企业安全投入层面，SMITH P M[5]等指出企业要加强对从事危险工作人员监管和监测的安全投入，对易造成伤害风险的人员信息进行识别和预防；WACHTER J K和YORIO P L[6]进一步探讨企业安全管理制度对员工行为的影响，并提出生产安全管理信息系统的开发和实施能有效降低事故发生率。从危险化学品风险评估层面，HAN Lu[7]等采用模糊综合评价法对不同危险化学品的风险进行分类评估，进而有效控制和管理危险化学品；ZHONG Yi-hua[8]等基于贝叶斯网络提出1种关于危险化学品风险预测和预警的新方法。危险化学品的安全生产监管涉及到危化品企业与政府监管部门这2个特定的博弈主体，其2者之间的利益博弈问题也是危化品安全监管的重点研究问题[9-10]。针对危化品企业与政府部门的博弈关系，沈斌等[11]运用信号模型理论研究政府主管部门与企业的相关博弈行为，提出改进政府安全生产管制效率的途径和方法；张艳楠和孙绍荣[12]以化工企业的经营效益和政府部门的社会效益为支付目标，基于“Stackelberg”博弈模型分析化工企业与政府部门之间的动态博弈过程，研究得出化工企业的生产安全投入取决于内部来自安全事故带来的平均损失和外部受到政府部门的罚款损失。但上述研究缺乏考虑博弈主体的有限理性及博弈双方间的交互影响。此外，现有研究没有深入分析危化品事故发生率及上级政府惩罚对博弈模型的影响。基于上述研究不足，将在危化品企业与政府监管部门有限理性假设下，通过引入危化品事故发生率，运用演化博弈理论对比分析危化品企业与政府监管部门行为策略的演化稳定均衡问题。

1　问题描述

在现实生活中，由于受到信息不确定性和环境复杂性等因素的影响，危化品企业和政府监管部门这2个博弈主体都具备有限理性特征。其中，危化品企业可以采取重视安全投入C或者不重视安全投入N2种策略，策略集合即STH={C,N}；政府监管部门可以采取监管严格K或监管不严格F2种策略，策略集合即STG={K,F}。主体博弈过程中，假设危化品企业采取重视安全投入策略C的比例为p，则采取不重视安全投入策略N的比例为1-p，p∈[0,1]，即P={p,1-p}；政府监管部门采取监管严格策略K的比例为q，采取监管不严格策略F的比例为1-q，q∈[0,1]，即Q={q,1-q}。

假定危化品企业安全投入成本为cH,危化品企业获得收益为V；当政府监管部门严格监督执法时，政府从危化品安全生产中获得收益为U，监管成本为cG；若危化品企业不重视安全生产，政府监管部门在监督检查过程中发现危化品和易燃易爆物品违法生产，存在重大安全事故隐患时，则对其进行停产、停业等整顿并处以罚款S；如果政府未加强严格监察，疏于安全检查时，危化品企业发生重大安全事故的机率为γ，若发生事故对危化品企业造成的经济损失为W，并会对其公司信誉等造成损失为θ，同时地方政府也会因危化品安全隐患排查不到位发生的重大安全事故承受经济损失为T，由此事件对政府信誉和社会形象造成损失为φ。

根据以上分析，可以得到政府监管部门与危化品企业2者之间的博弈收益矩阵，如表1所示。

表1　博弈收益矩阵

2　模型建立

由于危化品企业与政府监管部门多表现为有限理性，因此采用演化博弈中的复制动态方程[13-14]来描述其演化过程。

2.1　危化品企业复制动态方程与均衡分析

危化品企业的收益矩阵用矩阵ΠH表示为：

(1)

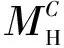
(2)

(3)

(4)

危化品企业的演化博弈复制动态方程为：

(5)

2.2　地方政府监管部门复制动态方程与均衡分析

政府监管部门的收益矩阵用矩阵ΠG表示为：

(6)

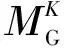
(7)

(8)

(9)

政府监管部门的演化博弈复制动态方程为

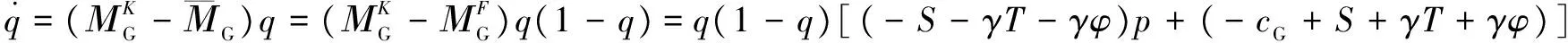
(10)

2.3　混合策略稳定性分析

由式 (5)和式(10)可以得到1个危化品企业与政府监管部门构成的2维动力系统(I)为：

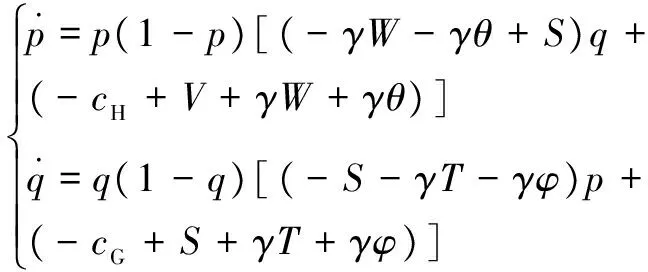
(11)

依据FRIEDMAN D[15]提出的方法，其2维动力系统平衡点的稳定性是由2个群体组成的2维动力系统的雅克比矩阵局部稳定性分析得到，系统(I)的雅克比矩阵为：

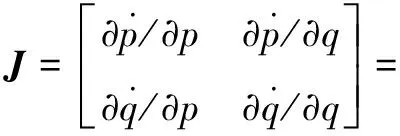
(12)

计算矩阵J在(0,0)，(0,1)，(1,0)，(1,1)，(p*,q*)这5个平衡点的行列式和迹的值及符号，由此判断出系统的局部稳定性。

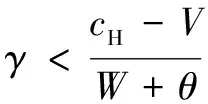
首先，计算出各点处的行列式和迹，如表2所示。

表2　系统(I)平衡点及其行列式和迹

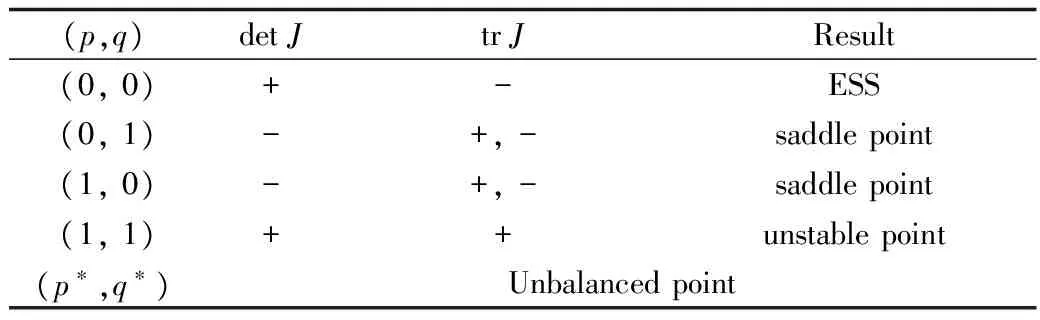
表3　条件(1)时，系统(I)平衡点及局部稳定性

命题1表明：危化品企业与政府监管机构是否采取安全投入和严格监管策略，与危化品事故发生率有直接关系，当危化品事故发生概率低于一定临界值时，危化品企业就会忽视安全生产投入，地方政府监管机构也会松懈安全监管。

3　上级政府惩罚机制下演化博弈模型

为促使危化品企业与地方政府监管部门采取安全投入和严格监管策略，避免发生重大危化品安全事故，上级政府可通过引入惩罚机制进行控制。假设上级政府对采取不重视安全投入策略N的危化品企业和采取监管不严格策略F的地方监管部门均给予惩罚Ψ。在重复博弈中，危化品企业和地方监管部门博弈的2维收益矩阵如表4所示。

表4　上级政府惩罚机制下博弈收益矩阵

同理，式(5)和(10)可以得到危化品企业与政府监管部门的演化博弈复制动态方程分别为式(13)和式(14)：

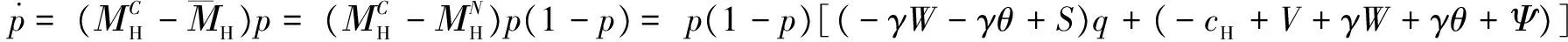
(13)

(14)

由式 (13)和式(14)可以得到1个危化品企业与地方监管部门构成的2维动力系统(II)为：

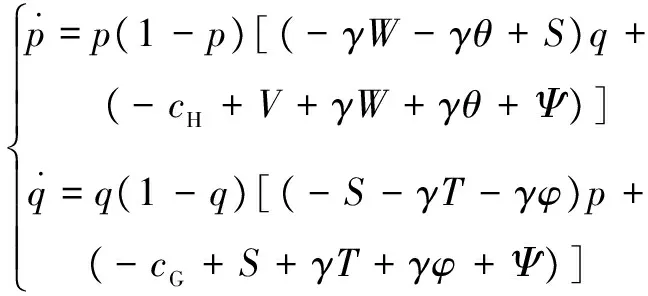
(15)

系统(II)的雅克比矩阵为：

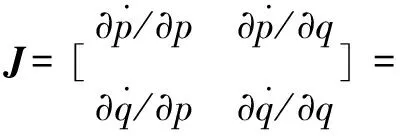
(16)

依据式(16)得到该2维动力系统(II)的行列式和迹分别为：

det(J)=(1-2p)[(-γW-γθ+S)q+(-cH+V+γW+

γθ+Ψ)]·(1-2q)[(-S-γT-γφ)p+(-cG+S+

γT+γφ+Ψ)]-q(1-q)(-S-γT-γφ)·p(1-

p)(-γW-γθ+S)

(17)

tr(J)=(1-2p)[(-γW-γθ+S)q+(-cH+V+

γW+γθ+Ψ)]+(1-2q)[(-S-γT-γφ)p+(-cG+

S+γT+γφ+Ψ)]

(18)

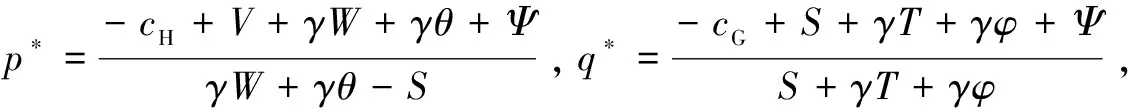
命题2当 满足条件(2)Ψ>-cH+S+V且Ψ>cG时，系统(II)存在唯一的演化稳定策略ESS为(1,1)。

证明首先,计算出各点处的行列式和迹如表5所示。

其次，针对表5，当满足条件(2) 时，对均衡点进行稳定性分析，结果如表6所示。

表5　上级政府惩罚机制下系统(II)平衡点及其行列式和迹

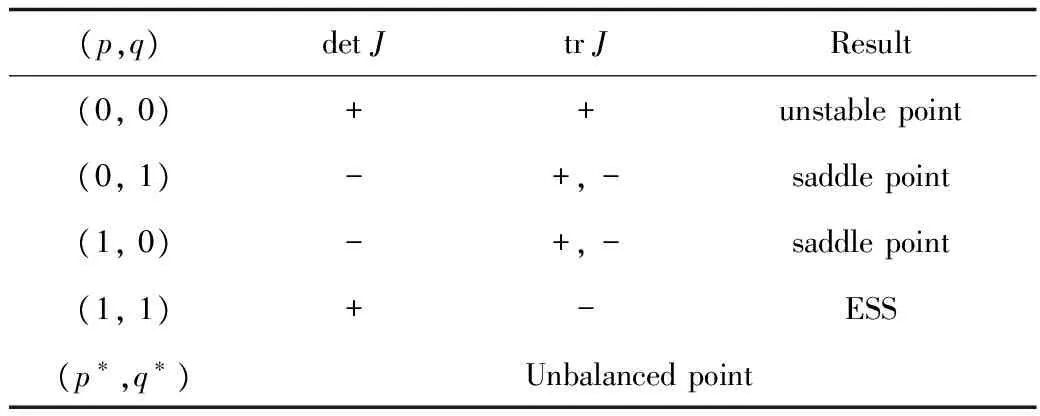
表6　条件(2)时,系统(II)平衡点及局部稳定性

从表6可以看出，当Ψ>-cH+S+V且Ψ>cG时，系统(II)存在唯一演化稳定点(1,1)、1个不稳定点(0,0)以及2个鞍点(0,1)、(1,0)。即系统(II)初始不管处于何种状态，最终都会演化至稳定点(1,1)，其表示危化品企业和地方政府监管部门最终的演化均衡策略是：重视安全投入，监管严格。

命题2表明：当上级政府惩罚力度，高于危化品企业未投入安全生产受到的处罚和安全投入获得收益与安全投入成本之差值，且同时高于地方政府监管部门安全监管成本时，能够有效地促使危化品企业和地方政府监管部门最终选择重视安全投入和严格监管策略。这为上级政府引导危化品企业与地方政府监管部门通过加大安全投入和严格监管预防危化品安全事故发生提供了理论指导依据。

4　情景推演仿真分析

下面对演化模型进行数值实验分析，通过时间T的变化进行情景推演模拟，观察随着时间变动对危化品企业和政府监管部门策略演化结果的影响。

4.1　情景1

危化品事故发生率γ=0.1情景下的危化品企业与政府监管部门策略演化。

对模型参数取值分别为：γ=0.1，V=5，W=3，θ=4，cH=10，T=4，φ=3，S=6,cG=9。对危化品企业初始比例p0分别取值为：0.3，0.5，0.8;时间段T取值[0,200]。政府监管部门初始比例q0分别取值为：0.3，0.5，0.8；时间段T取值[0,50]。仿真过程如图1和图2所示，其中横坐标Time表示时间段，纵坐标p、q分别表示危化品企业和地方监管部门策略比例变化。

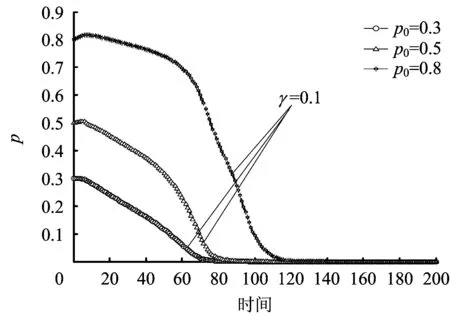
图1　危化品企业采取无安全投入策略演化过程Fig. 1　Without safety investment strategy evolutionary process of hazardous chemical enterprises

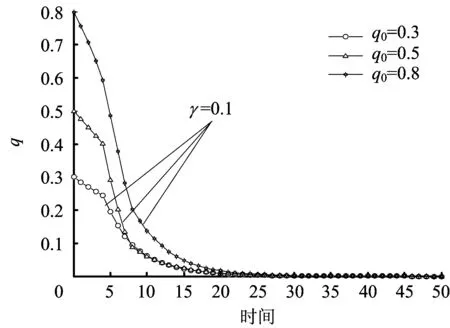
图2　地方监管部门采取监管不严格策略演化过程Fig.2　Lax regulation strategy evolutionary process of local government

4.2　情景2

地方政府承受危化品事故经济损失T和信誉损失φ增大情景下的策略演化。

对地方政府承受危化品事故经济损失T和信誉损失φ取值分别为：T=22，φ=18，其他参数同情景1取值。图3和4中横坐标Time表示时间段，纵坐标Fraction表示危化品企业与地方监管部门采取重视安全投入和监管严格策略的比例。初始状态策略的比例取值分别为：p0=q0=0.3，p0=q0=0.5，仿真过程如图3、图4所示。

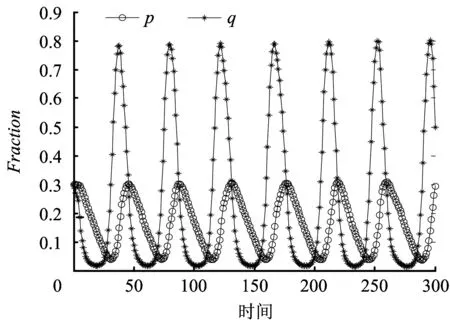
图3　p0=q0=0.3下危化品企业与地方监管部门策略选择演化过程Fig.3　Strategy selection evolutionary process of hazardouschemical enterprises and local government when p0=q0=0.3

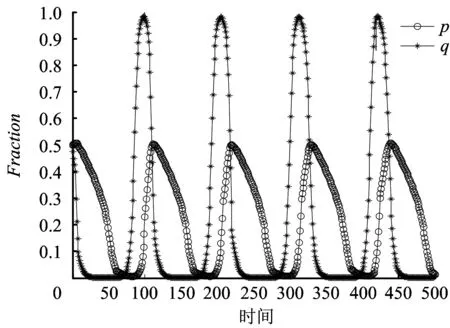
图4　p0=q0=0.5下危化品企业与地方监管部门策略选择演化过程Fig.4　Strategy selection evolutionary process of hazardous chemical enterprises and local government when p0=q0=0.5

从图3和图4，可以发现随着地方政府承受危化品事故经济损失T和声誉损失φ增大时，危化品安全监管管理过程中出现监管严格和监管过松的周期性波动，而危化品企业在地方政府周期性监管下也出现增加安全投入和未增加安全投入的周期性波动现象。对比图3和图4，可以看出周期性波动的振幅与系统演化的初始状态策略比例有直接关系，当初始状态地方监管部门选择严格监管的比例越大，周期性波动的振幅越大。这表明尽管随着危化品事故造成的经济和信誉损失增大，迫使地方政府监管部门改变长期监管过松的策略，但还是会出现监管严格和监管松懈的周期性波动情景。为避免地方政府监管出现周期性波动现象，可通过引入上级政府惩罚机制进行控制。

4.3　情景3

上级政府惩罚下的危化品企业与地方政府监管部门策略演化。

对上级政府惩罚力度Ψ分别取值为：0.2，10，15，初始状态策略的比例分别取值为：p0=0.3，q0=0.3，其他参数同情景2，仿真过程如图5所示。

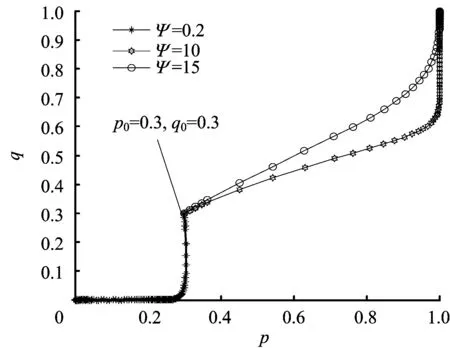
图5　在惩罚Ψ不同取值下危化品企业与政府部门策略选择演化过程Fig.5　Strategy selection evolutionary process of hazardous chemical enterprises and local government when Ψ=0.2,10,15

从图5中可以看出，当惩罚Ψ=10时，其满足条件Ψ>-cH+S+V且Ψ>cG，即Ψ>1且Ψ>9，此时地方政府监管部门将选择严格监管策略，同时危化品企业也会选择重视安全投入策略，加大安全生产投入，避免发生政府安全生产监管过松和监管过严的周期性交替现象。

5　结论

1)当危化品事故发生率低于临界值，即事故发生率较低时，危化品企业与政府监管部门都会忽视安全投入和严格监管。

2) 危化品安全监管管理过程中会交替出现监管严格和监管过松的周期性波动情景，表明需要政府部门始终加强安全监管，提高安全生产监督防范意识。

3)引入上级政府的惩罚机制能有效促使地方政府部门和危化品企业选择严格监管和安全投入策略，这说明上级政府应当制定合理的惩罚机制，包括加大对地方政府监管事故问责力度、政府公信度形象考察力度、危化品企业违规处罚力度等，避免重大危化品安全事故的发生。

4)危化品安全监管演化博弈模型适用于危化品安全生产监管问题的分析和研究，可为政府监管危化品安全生产提供新的思路和对策建议。

[1]冯领香，李书全，陈向上．企业生产安全投入与监管的演化博弈[J]．数学的实践与认识，2012，42(8)：76-84．

FENG Lingxiang, LI Shuquan, CHEN Xiangshang. Evolution game upon enterprise work safety investment & regulation[J]. Mathematics in Practice and Theory, 2012, 42(8):76-84.

[2]邹晓川，王存，张雪，等．基于“三圆环事故致因理论”的危险化学品安全管理分析[J]．西南师范大学学报(自然科学版)，2015，40(8)：134-139．

ZOU Xiaochuan, WANG Cun, ZHANG Xue, et al. On safety management of dangerous chemicals by “Three ring accident causing theory”[J].Journal of Southwest China Normal University(Natural Science Edition), 2015, 40(8): 134-139.

[3]RENIERS G L L, Ale B J M, Dullaert W, et al. Designing continuous safety improvement within chemical industrial areas[J]. Safety Science, 2009, 47(5): 578-590.

[4]MAKIN A M, WINDER C. A new conceptual framework to improve the application of occupational health and safety management systems[J]. Safety Science, 2008, 46(6): 935-948.

[5]SMITH P M, SAUNDERS R, LIFSHEN M, et al. The development of a conceptual model and self-reported measure of occupational health and safety vulnerability[J]. Accident; Analysis and Prevention, 2015, 82(8): 234-243.

[6]WACHTER J K, YORIO P L. A system of safety management practices and worker engagement for reducing and preventing accidents: An empirical and theoretical investigation[J]. Accident; Analysis and Prevention, 2014, 68(SI): 117-130．

[7]HAN Lu, SONG Yong-hui, DUAN Liang, et al. Risk assessment methodology for Shenyang Chemical Industrial Park based on fuzzy comprehensive evaluation[J]. Environmental Earth Sciences, 2015, 73(9): 5185-5192.

[8]ZHONG Yi-hua, LIU Yu-xin, LIN Xu-xu, et al. The method of oilfield development risk forecasting and early warning using revised bayesian network[J]. Mathematical Problems in Engineering, 2016,2016(4): 1-10.

[9]Reniers G, Pavlova Y. Introduction: Why a Book on Game Theory for Safety Within the Chemical Industry?[M]. Using Game Theory to Improve Safety within Chemical Industrial Parks. Springer London, 2013: 1-11.

[10]RUSSELL D, SIMPSON J. Emergency planning and preparedness for the deliberate release of toxic industrial chemicals[J]. Clinical Toxicology, 2010, 48(3): 171-176.

[11]沈斌，梅强，刘素霞，等．基于信号模型理论的企业安全生产管制研究[J]．系统管理学报，2011，20(3)：276-286．

SHEN Bin, MEI Qiang, LIU Suxia , et al. A study on regulating enterprise safety production based on signaling model[J]. Journal of Systems & Management, 2011, 20(3): 276-286.

[12]张艳楠，孙绍荣．基于Stackelberg博弈模型的化工企业安全生产管理机制治理研究[J]．中国管理科学，2016，24(3)：159-168．

ZHANG Yannan, SUN Shaorong. Research on safety production management mechanism in enterprise based on stackelberg game model[J]. China Journal of Management Science, 2016, 24(3): 159-168.

[13]WU Dan, ZHOU Liang, CAI Yueming, et al. Energy-Aware dynamic cooperative strategy selection for Relay-Assisted cellular networks: an evolutionary game approach[J]. IEEE Transactions on Vehicular Technology, 2014, 63(9): 4659-4669.

[14]LIU Dehai, XIAO Xingzhi, LI Hongyi, et al. Historical evolution and benefit-cost explanation of periodical fluctuation in coal mine safety supervision: An evolutionary game analysis framework[J]. European Journal of Operational Research, 2015, 243(3): 974-984.

[15]FRIEDMAN D. Evolutionary games in economics[J]. Econometrica : Journal of the Econometric Society, 1991, 59(3): 637-666.