能量高效超密集网络的最优部署
2017-04-13
(南京邮电大学通信与信息工程学院,江苏 南京 210003)
能量高效超密集网络的最优部署
葛亮,王志旭
(南京邮电大学通信与信息工程学院,江苏 南京 210003)
为使能量效率最大化,采用随机几何方法对多小区多用户MIMO蜂窝网络的上行链路进行建模,改进系统功耗模型,得到一个关于基站密度、发送信号功率、基站天线数、小区用户数以及导频复用因子的能量效率最大化问题。求解该问题,可得到最优的网络部署方案以及各最优参数与硬件特性、传播环境之间的关系。仿真与数值计算结果显示,超密集网络部署可以显著提高能量效率,但是随着基站密度的进一步增加,能量效率的提升很快饱和。更有趣的是,能量效率最优化所确定的部署方案恰为大规模MIMO情形。
能量效率;超密集网络;大规模MIMO;多用户MIMO;上行链路
1 引言
随着移动通信的发展和新应用的产生,网络流量空前增长[1],与此同时,通信能耗以及相关的污染问题已成为主要的社会经济问题[2],5G系统一方面需要更高的网络吞吐量,一方面又要求更低的功耗[3],二者相互矛盾,但目前普遍认为,充分的网络密集化可以解决该矛盾。因此更高的频谱效率(spectralefficiency,SE)和能量效率(energy efficiency,EE)将会是下一代5G网络的核心目标之一。
网络密集化主要包括两个方面:小蜂窝[4,5]和大规模MIMO[6,7],前者可以理解为超密集网络,可简单地通过在热点地区高密度地部署小蜂窝来实现;与此不同,大规模MIMO技术通过使用成百上千根偶极天线组成天线阵列来改变传统基站。总的来说,为了提高网络整体的能量效率,收益和开销必须进行适当的权衡。能量效率定义为效益成本比[8],即区域频谱效率(area spectral efficiency,ASE)和区域功率消耗(area power consumption,APC)的比值。

已有的文献主要针对单小区[9,10],或针对多小区小蜂窝网络的下行链路(downlink,DL)[11,12],而本文针对密集网络多用户MIMO上行链路(uplink,UL)进行分析;同时,密集网络不同于传统蜂窝网规则的六边形镶嵌,基站通常随机且密集地分布,因此本文采用随机几何(stochastic geometry)[13]的方法对蜂窝网络进行建模;此外,大多数现有文献中的功耗模型仅考虑电路功耗和基站侧的收发机功耗,而本文对参考文献[8]做出改进,提出了一种更详细且更切合实际的功耗模型。利用上述模型和方法,得出关于基站密度、基站天线数、小区用户数、发射功率以及导频复用因子的最优化问题,通过求解该问题最终得出最优网络部署策略。
本文使用的符号记法:E{·}表示随机变量的期望;||·||和|·|分别表示 2-范数和绝对值;IM表示M×M的单位阵;CN(·,·)表示多维旋转对称复高斯分布;C、Z+和R分别表示复数集、正整数集和实数集。
2 系统模型
2.1 随机几何建模
本文采用随机几何的方法对蜂窝网络的上行链路进行建模:基站(base station,BS)在二维平面(R2)内随机分布,服从密度为 λ的平稳泊松点过程 Φλ(homogeneous PPP)[14],λ表示基站的密度。设任意一个面积为 A的区域(单位为km2)内的基站数目为N(A),则N(A)~Poisson(λA),即:
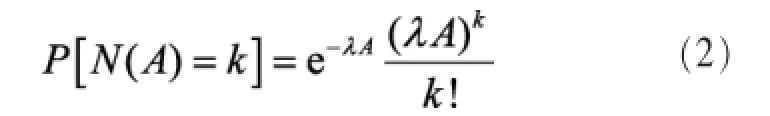
每个BS配置有M根天线,并可同时服务K个单天线用户设备(user equipment,UE)。假设每个UE都连接到离它最近的基站,则基站的覆盖区域呈现出不规则的沃罗诺伊图(Voronoi diagram),如图1所示。
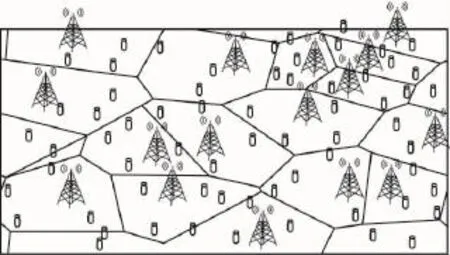
图1 BS与UE的分布
依据泊松点过程的平移不变性,可以以一个典型UE的位置为坐标原点进行性能分析。假设这个典型UE在本小区内的K个UE中的标号为k,即UEk,设UEk连接到的基站为典型基站,表示为BS0∈Φλ,那么易得引理如下。
引理1典型用户UEk与其服务基站BS0之间的距离d00k服从瑞利分布:
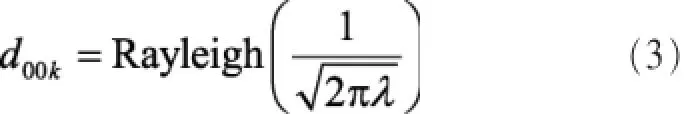
2.2 信道模型
假设信道响应建模为块衰落(block-fading),即在一个相干带宽 WC、相干时间 TC的数据块内,信道传输特性保持不变,该数据块可承载的符号数共S=TCWC,这S个符号一部分用于发送导频信号,另一部分用于发送数据信号。
用户UEk与基站 BSl之间的信道响应如图 2所示,小区j中的用户UEk与基站 BSl之间的信道响应为hijk∈CM,由于块衰落,在同一个资源块中hijk可以看作一个随机常量,而不同资源块之间hijk相互独立。由于瑞利衰落信道能很好地匹配M较小或较大情况下的非视距传输,因此可设瑞利衰落信道,其中 dljk表示UEk和BSl之间的传播距离(单位为km);α>2表示大尺度衰落的路径损耗指数;而参数ω表示参考距离1 km处的路径损耗(距离不相关,如穿墙损耗)。
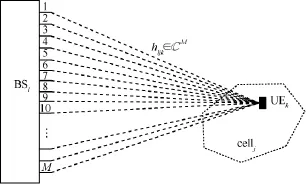
图2 用户UEk与基站BSl之间的信道响应
2.3 功率控制策略
由于远近效应,功率控制是多用户MIMO上行链路必须要考虑的问题。本文采用参考文献[15]中的统计信道反演功率控制:其设置小区j中UEi的发送功率(单位为J/符号),其中ρ≥0为功率控制系数。那么,UEi的平均发送功率可以表示为,结合引理1得平均发送功率为:
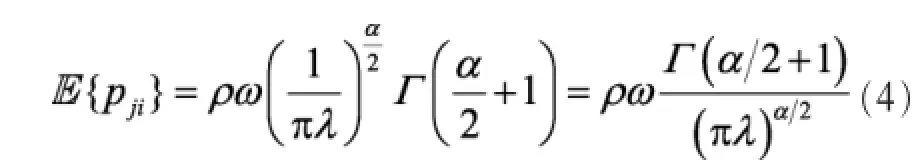
经过信道衰减,BSj接收到的 UEi信号的总平均功率为,不难发现,基站中的任一UE的发送信号在本基站侧的平均接收功率都是相等的,从而达到了功率控制的目的,克服了远近效应。
2.4 收发机硬件失真
任何实际的无线收发机都不可能是完全理想的,或多或少都会受到硬件失真的影响。之前的系统分析都很少考虑硬件失真[16],本文主要关注用户设备的发送失真,而忽略基站侧的硬件失真,因为BS通常可以使用高规格、高精度的硬件,而UE一般为廉价的硬件,易受硬件失真的影响。
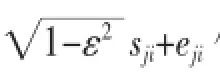
基于上述假设,典型基站BS0的接收信号y0∈CM中包括本基站内K个用户的信号、其他基站的众多用户的干扰信号以及高斯白噪声,为:
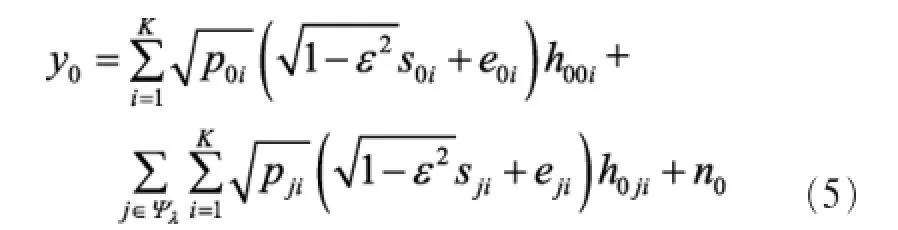
其中,n0~CN(0,σ2IM),表示接收噪声,噪声方差为σ2。ψλ表示基站的PPP点集Φλ中除典型基站BS0之外其他基站点构成的集合,即
2.5 导频污染
众所周知,接收信号y0的相干处理需要知道上行链路的信道信息h00i,i=1,…,K。假设一个相干资源块S个符号中有B个符号用于发送导频,可定义β=B/K≥1为导频复用因子,则有βK=B≤S。
由典型用户UEk发送、典型基站BS0接收的导频符号会受到其他小区中某个复用该导频符号的用户的干扰。当小区j中有用户UEk使用与典型用户相同的导频序列时,将会导致导频污染问题,发生的概率为K/B。类似地,若小区j中没有用户使用与典型用户相同的导频序列,则不会产生导频污染问题,概率为1-K/B=1-1/β。另外,为简单起见,本文采用MMSE信道估计,容易得信道估计值
3 平均频谱效率计算
3.1 用户遍历容量
基站采用最大比合并 (maximal-ratio combining,MRC)相干处理。对于典型用户 UE发送的符号,基站利用信道估计值进行相干检测,也就是说,对式(5)的 y0进行MRC处理其中υ00k∈C表示比例因子。本文采用许多大规模MIMO经典文献中常用的遍历容量的下界公式来表示频谱效率。
引理2采用MRC,对任意给定的ψλ和UE位置,典型用户的遍历容量的一个下界为[17]:
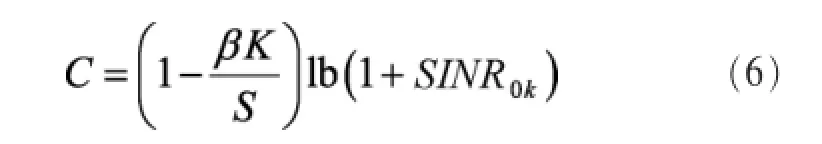
其中,(1-βK/S)因子表示导频开销,而有效SINR0k的表达式如式(7)所示。
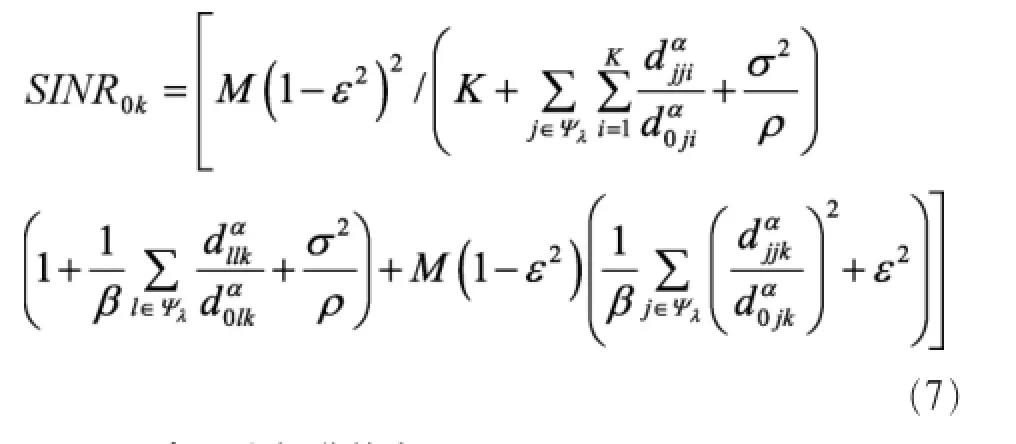
3.2 用户平均频谱效率
对式(6)关于 PPPψλ和UE位置求期望,就可得到用户的平均频谱效率。
引理3如果接收端采用MRC接收处理技术,则上行链路平均频谱效率SE(单位bit/(符号·用户))的下界为:
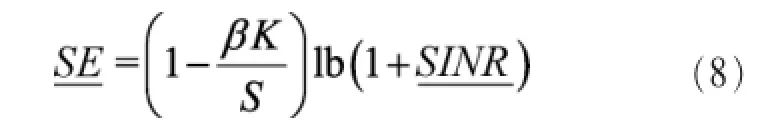
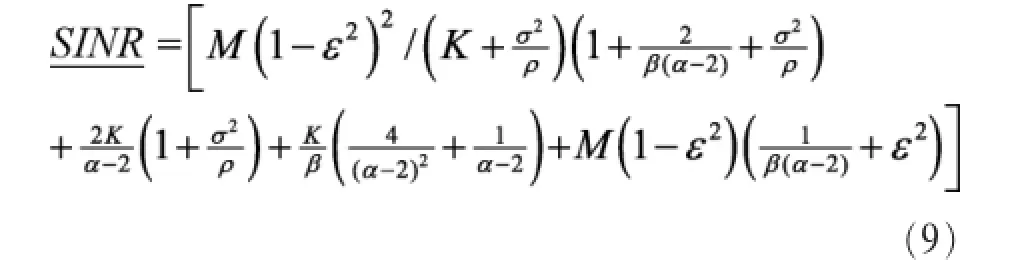
值得注意的是,式(8)的平均频谱效率是 SE的紧下界,后面将通过仿真来证明(如图 3所示)。观察式(9),易发现随着基站天线数M增多,接收平均信噪比也随之增大,这得益于多天线相干处理的阵列增益;而当K增大时,减小,因为更多的UE意味着更多的干扰;随ε增大而减小,即硬件失真在一定程度上影响着,从而影响频谱效率;另外,与基站密度λ无关,这是因为功率控制的存在,保证了每个UE的信号到达本基站的接收功率是一定的。
4 能量效率最大化
4.1 系统功耗模型
网络的整体功耗不仅包括发射信号功耗,还包含电路功耗:模拟器件、数字信号处理、回程信令以及其他(如制冷和供电损耗)的功率消耗。大多数现有的文献中仅简单地把电路功耗建模为固定值[18],或者仅考虑基站侧的收发机功耗[11],本文提出了一种更详细且更切合实际的功耗模型,结合式(4)可得APC为:

其中,η∈(0,1]表示线性功率放大器的效率;C0表示单个基站的静态功耗;D0M表示基站收发机组件的功耗,与基站天线数成正比。
除此之外,该模型还额外考虑了用户设备收发机功耗、基站信号处理功耗和编解码的功耗:C1K表示用户设备收发机的功耗,与用户数成正比;D1MK表示基站侧信号处理的功耗;A·ASE表示编解码的功耗,与比特数成正比。参照参考文献[8],选取参数见表1。
4.2 能量效率最大化问题
本文的目标是能量效率的最大化,根据定义并结合式(8),可得ASE为:

至此,根据能量效率的定义,可以得到本文的关键问题:对于任意给定的资源块S、传播参数(α,ω)以及硬件特性(η,ε,A,C0,C1,D0,D1),如何确定参量θ=(β,ρ,λ,K,M)来解决下面的有约束EE最大化问题:
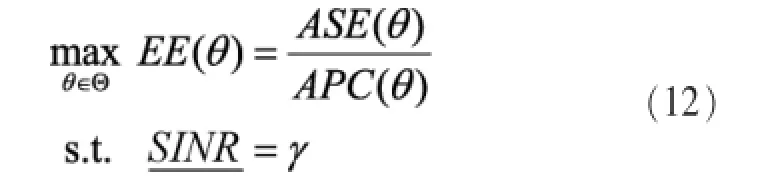
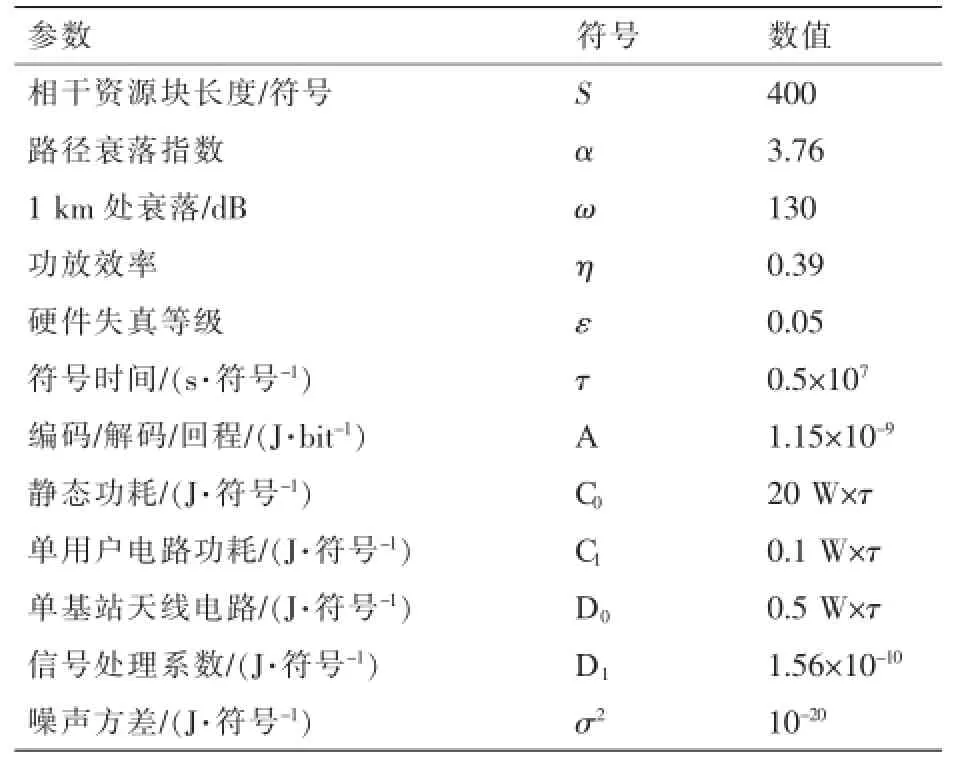
表1 仿真参数
可行域为Θ={θ∶ρ≥0,λ≥0,β≥1,(M,K)∈Z+,Kβ≤S}
下面各节将对上述最优化问题进行详细分析。
4.3 最优导频复用因子
定理1对于式(12)的任意可行集{ρ,λ,K,M},其约束条件可转化成关于β的条件。
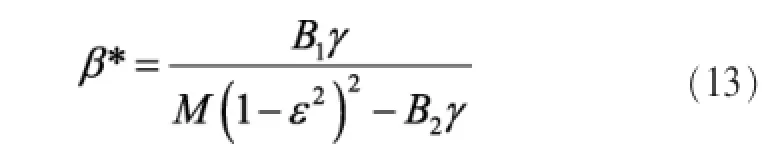
证明:利用式(9)将β表示成关于{K,M,ρ,λ}的函数,即得式(13)。
其中:

较大的β意味着更准确的信道估计,而由式(13)可以发现:β*关于K单调递增,因为增大K意味着更多的小区间干扰,为保证信噪比不变,只有通过增大β,抑制导频污染,提高信道估计的准确性;而β*关于ρ单调递减,这是因为若增大ρ,则UE发送功率增大,信噪比提高,不需要很大的β就能保证可靠。
4.4 最优基站密度和发射功率
基于定理1,将β*代入式(12)的目标函数EE(θ),约去 β参数可得新的目标函数EE(β*),易得基站密度 λ和功率控制系数ρ的最优值。
定理 2EE(β*)是关于λ的单调增函数,当λ→∞时,能量效率达到最大化。同时,在λ→∞的条件下,EE(β*)是关于ρ的增函数,故ρ→∞时能量效率达到最大化。
定理2说明,为使能量效率最大化,应使基站密度λ尽可能大。这一结果看似不太切合实际,因为更密集的网络意味着更多的用户间干扰,但这个问题已通过功率控制策略得以解决。另外,随着λ变大,基站变密,APC中的信号发送功率部分变得微乎其微,可以忽略不计,这种情况下APC中的电路功耗成为主要功耗。实际情况下,基站密度λ不可能无限大,后面的数值仿真结果也表明,当λ增大到102以上时,EE会趋于饱和,而在超密集网络中,基站密度远大于此,因此后面以λ→∞为条件的最优化分析是合理的。
4.5 最优基站天线数和单小区用户数
利用定理1(β*)和定理2(λ→∞,ρ→∞),式(12)可简化为:
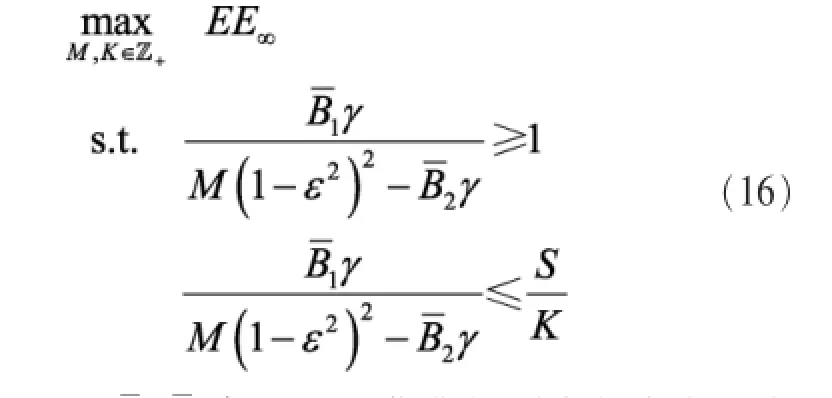
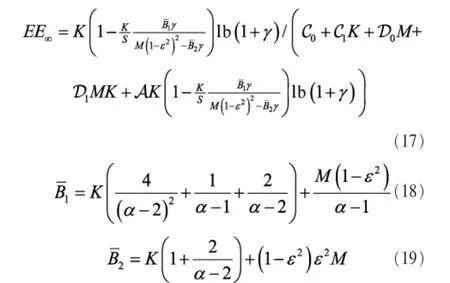
至此,式(16)只包含2个最优化变量M和K,根据定义,M和K必须为正整数,现为了便于对该最优化问题求解,将该限制条件放宽为实数,先求实数最优解,再寻找整数最优解。为便于表示,用M和K的比值来代替M,即对和K这两个自变量求解最优化问题。
定理3将式(16)放宽到实数域,则对于任一给定可行的,在可行域内所有K的取值中,存在K*使能量效率(EE)最大化。
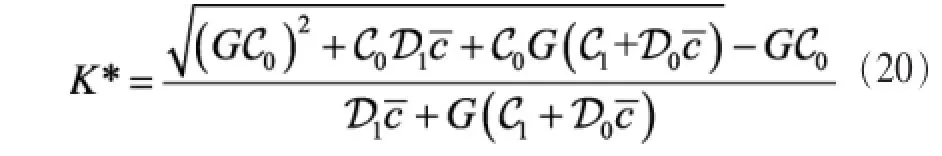
其中:
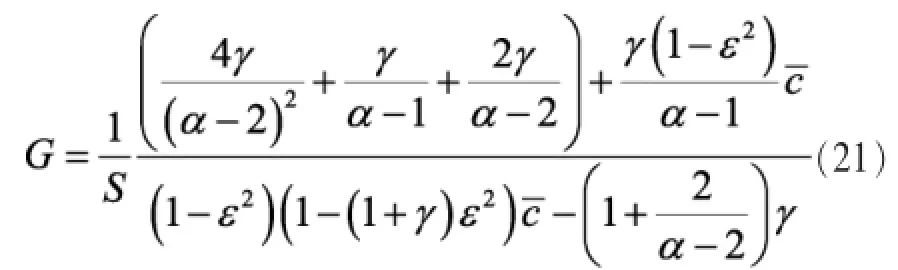
证明: 若c为定值,将M=cK、R=1b(1+γ)和G=β/S代入式(17),可得目标函数EE为关于K的凸函数,求其驻点即可得K*。
定理4将式(16)放宽到实数域,则对于任一给定的K>0,在可行域内所有c的取值中,存在c*使EE最大化。
若满足式(16)中第1个约束条件,则:
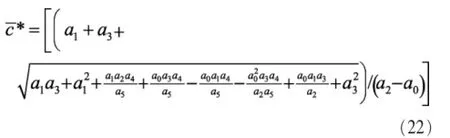
否则:
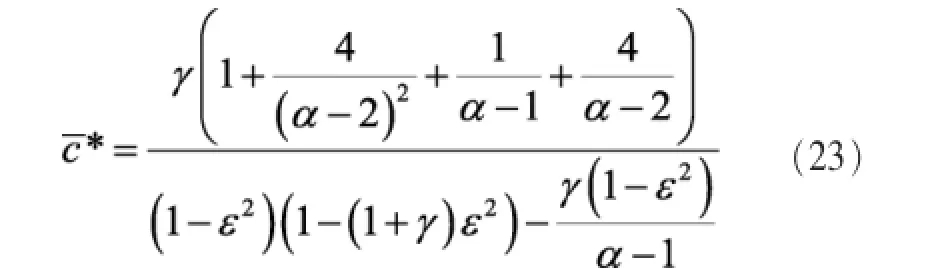
式(22)和式(23)中使用的各参数如下:
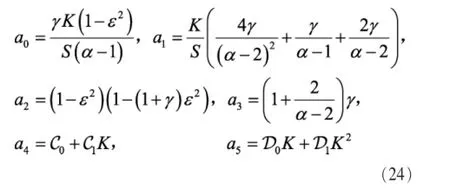
证明与定理3的证明类似。
另外,定理 3和定理 4同样揭示了功耗系数 C0、C1、D0、D1和A是怎样影响最优点K*和M*的。从式(20)可以看出,K*随静态功耗C0递增,而随C1、D0和D1递减。同样地,M*随C0、C1递增,而随D0、D1递减。
利用定理3和定理4,可以设计出一个迭代优化算法以解决上述最优化问题(实数域),具体步骤如下。
步骤 1确定式(16)的一个可行起始点(M,K),即
步骤2利用定理3,固定c值,求得最优K*;
步骤3利用定理4,固定步骤2中所确定的K*,求得最优
步骤4重复步骤2、步骤3直到收敛。
因为EE有有限个上界,且在每次迭代中,EE单调递增,所以该算法必定收敛。容易证明 EE是关于(M,K)的凸曲面,因此迭代算法必定收敛到全局最优解(K**,M**)∈R2。
迭代优化算法得到的实值解(K**,M**)是寻找整数最优解的起点,整数最优解必然在(K**,M**)附近的凸面上,因此可在实值解附近搜寻所有的整点,比较 EE以找到最优整数解。
5 仿真与数值分析
本节将通过仿真来证明引理3的平均频谱效率(SE)下界表达式的准确性,并证实第 4节中的一些基本结论。本节中的仿真与数值计算所使用的参数见表1,其中假设相干资源块长度S=400(TC=4 ms,WC=100 kHz),总带宽为20 MHz。
5.1 最大化能量效率
为了说明在实际情况下,λ需要多大就可以应用定理2的渐进结果,本节通过仿真和数值计算,画出最优EE关于λ的图像,如图3所示。图3中考虑了3种不同的SINR约束:γ∈{1,3,7},对于这 3种情况,分别画出了两条曲线,一条是引理3的理论值曲线,另一条则是蒙特卡洛仿真曲线。
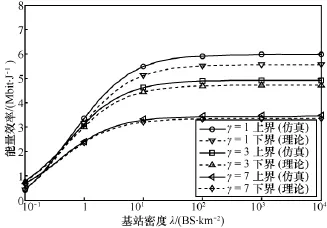
图3 最优能量效率与基站密度的关系
对于同一γ值,两曲线整体走向近似,之间的差距不大,且随着γ增大,两曲线差距缩小,这就验证了引理3的SE表达式的准确性。还发现增大λ可提高EE,这意味着超密集网络部署是最大化EE的一个好方法,但是,当λ大到一定程度之后,EE趋于饱和,此时增大λ不再能显著提高EE。观察图3还可以发现,饱和范围λ在10~100内,而当代都市密集网络部署的λ一般在 103以上,也就是说,定理2的结论在大多数实际的密集网络部署中都是合理的。
图4表示γ=3时,EE关于M和K的函数图像,得到的最优值点为 (M*,K*)=(100,11),导频复用因子 β*= 7.096,而EE最大值为4.725 6 Mbit/J。有趣的是,基站使用 100根天线服务 11个单天线用户,正属于大规模MIMO。因此,基站配置了大规模的天线阵列可有效抑制密集网络中严重的小区间干扰,最大化能量效率。
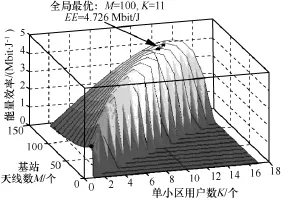
图4 γ=3时,能量效率关于M和K的全局最优化
迭代优化算法的结果也在图4中用黑点标记出来。迭代的起始点设置为(M,K)=(10,1),正如所看到的,算法经过3次迭代就收敛到实数最优解(M**,K**)=(95.23,10.54),此时EE=4.727 6 Mbit/J。该实数最优解对应的EE仅比整数最优解的EE高0.04%,这说明EE在最优解附近是很平坦的。
图5是全局最优时各功耗占比情况,其将式(10)中各分项分布情况清晰地表示出来(由于功率控制策略,密集网络中信号发送功率很小,可忽略)。可以看出,静态功耗C0和基站收发机功耗D0M为最主要的功耗,所以如果想要从硬件角度提高能量效率,应优先从这两方面考虑。
5.2 收发机硬件失真的影响
下面以λ→∞的EE饱和状态分析收发机硬件失真对能量效率的影响。如图6所示,正如所预想的那样,EE随着ε的增大而减小,这是因为式(9)中有用信号功率随(1-ε2)2衰落。另外当信噪比较小时,比如γ=1,即便硬件失真等级ε增大,能量效率的损失也比较小;而当信噪比较大时,比如γ=7,ε增大将造成能量效率明显降低。所以可以得到如下结论:适度的硬件失真等级对于能量效率的最优化设计的影响是可以忽略的。
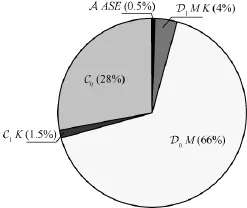
图5 APC中各项功耗占比分布
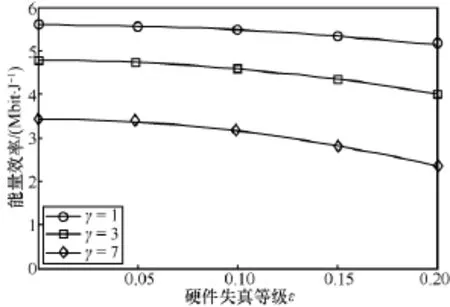
图6 硬件失真等级ε对能量效率EE的影响
5.3 固定用户密度的能量效率最优化
之前还未考虑用户密度的问题,根据之前的假设,每个基站服务K个用户,而基站密度为λ,那么相应的用户密度应为Kλ,因此,随着基站密度增大,平均用户密度也随之增大。为验证该模型的合理性,假设平均用户密度固定为μ,基站密度则为λ=μ/K,也就是在求解式(12)时,需再加上一个约束条件:

下面分析这一额外的约束条件会怎样影响前面的分析结果。这里将考虑从μ=100(农村)到μ=105(商场)的各种可能情境。
图7是平均SINR等级γ=3的条件下,最优EE关于用户密度μ的函数图像。图7中提供了两个参考情境进行比较:SIMO(M,K)=(10,1)和大规模MIMO(M,K)=(100,11),即第4.1节中得到的最优解。很显然,在这两种参考情境下,M和K为定值,仅对β、λ和ρ求最优化。
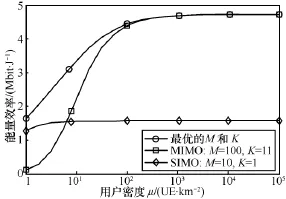
图7 最优能量效率EE与用户密度的关系
首先,可以发现当μ足够大时,最优EE将和用户密度无关。对于最优化情境和MIMO情境,这种饱和特性将在μ≥100时产生,而对于SIMO情境,μ≥2时就逐渐饱和。前面提到,未来平均用户密度的范围 μ∈[102,105],恰好处在饱和范围内,因此对于实际密集网络部署,用户密度的高低基本不影响EE的最优。
其次,观察图7中MIMO和SIMO两条曲线,可以发现当用户密度较低(比如 μ≤8)时,大规模MIMO情境下的能量效率EE反而要低于SIMO情境,也就是说,SIMO在低用户密度时效果更好。但是SIMO在用户密度稍微高一些时就饱和,且饱和时的能量效率明显低于另外两种情况,比最优的能量效率低约3.01倍。另外,对于同一用户密度的实际环境,SIMO需要10倍的基站密度,这会大大增加基站部署的开销。综上所述,相比于SIMO,大规模MIMO是更优的选择。
6 结束语
蜂窝网络中,网络致密化是获得高能量效率的关键,其既可以通过部署更密集的基站实现,也可以通过给每个基站配置更多的天线来实现。为了寻求最优的密集网络配置,本文基于随机几何方法建模,公式化上行链路EE最大化问题。利用平均频谱效率的下界计算式,并在已有基础上改进了功耗模型,得到一个关于基站密度、发射信号功率等级、基站天线数、单小区用户数和导频复用因子5个参量的最优化问题。然后通过求解该最优化问题,得到最优变量的闭式表达式,从中可以看出各系统参数与功耗模型各成分之间的相互关系,并给实际的网络部署和设计提供有价值的参考。本文虽针对上行链路,但下行链路也能得到相似的结论。
分析结果显示,减小各小区的尺寸(即小蜂窝)毫无疑问可以提高能量效率,但是随着基站密度的进一步增大,能量效率的提高呈现饱和状态,此时基站密度的增大不再能显著提高能量效率。值得注意的是,此时电路功耗为主要功耗,发射信号的功耗可忽略不计。另外,为基站增加额外的天线也可以带来 EE的显著提升,第4.1节的数值计算结果显示,基站天线数为 100、小区用户数为 11时,可获得最大的能量效率,这正属于大规模MIMO。此外,本文还考虑了系统的硬件失真,结果显示,少量的硬件失真对于能量效率的最优化设计的影响不大。
[1]AGIWAL M,ROY A,SAXENA N.Next generation 5G wireless networks:a comprehensive survey[J].IEEE Communications Surveys&Tutorials,2016,18(3):1617-1655.
[2]FEHSKE A,FETTWEIS G,MALMODIN J,et al.The global footprint of mobile communications:the ecological and economic perspective[J].IEEE Communications Magazine,2011,49(8): 55-62.
[3]ANDREWS JG.,BUZZI S,CHOI W,et al.What will 5G be[J]. IEEE Journal on Selected Areas in Communications,2014,32(6): 1065-1082.
[4]HOYDIS J,KOBAYASHI M,DEBBAH M.Green small-cell networks[J].IEEE Vehicular Technology Magazine,2011,6(1): 37-43.
[5]KAMEL M,HAMOUDA W,YOUSSEF A.Ultra-dense networks: a survey[J].IEEE Communications Surveys&Tutorials,2016, 18(4):2522-2545.
[6]LARSSON E G,TUFVESSON F,EDFORS O,et al.Massive MIMO fornextgeneration wirelesssystems[J].IEEE Communications Magazine,2014,52(2):186-195.
[7]NGO H Q,LARSSON E G,MARZETTA T L.Energy and spectral efficiency of very large multiuser MIMO systems[J].IEEE Transactions on Communications,2013,61(4):1436-1449.
[9]MUKHERJEE S,MOHAMMED S K.Energy-spectral efficiency trade-off for a massive SU-MIMO system with transceiver power consumption [C]//2015 IEEE International Conference on Communications (ICC),June 8-12,2015,London,UK.New Jersey:IEEE Press,2015:1938-1944.
[10]MOHAMMED S.Impact of transceiver power consumption on the energy efficiency of zero-forcing detector in massive MIMO systems[J].IEEE Transactions on Communications,2014,62(11): 3874-3890.
[11]LIC,ZHANG J,LETAIEF K B.Throughput and energy efficiency analysis ofsmall cellnetworks with multi-antenna base stations[J]. IEEE Transactions on Wireless Communications,2014,13(5): 2505-2517.
[12]REN Q,FAN J,LUO X,et al.Analysis of spectral and energy efficiency in ultra-dense network[C]//2015 IEEE International Conference on Communication Workshop (ICCW),June 8-12, 2015,London,UK.New Jersey:IEEE Press,2015:2812-2817.
[13]BACCELLI F,B L ASZCZYSZYN B.Stochastic geometry and wireless networks:volume I theory[J].Foundations and Trends in Networking,2009,3(3-4):249-449.
[14]HAENGGI M,ANDREWS J G,BACCELLI F,et al.Stochastic geometry and random graphs for the analysis and design of[J].IEEE Journal on Selected Areas in Communications,2009,27(7): 1029-1046.
[17]YANG H,MARZETTA T L.Capacity performance of multicell large-scale antenna systems[C]//51st Annual Allerton Conference on Communication,Control,and Computing,October 2-4,2013, Monticello,Illinois,USA.New Jersey:IEEE Press,2013: 668-675.
[18]XU J,QIU L.Energy efficiency optimization for MIMO broadcast channels[J].IEEE Transactions on Wireless Communications, 2013,12(2):690-701.
Optimal deploym ent of energy-efficient ultra-dense network
GE Liang,WANG Zhixu
College of Telecommunications&Information Engineering,Nanjing University of Posts and Telecommunications,Nanjing 210003,China
In order to maximize energy efficiency,the stochastic geometry method was used to model the uplink of a multi-cellmulti-user MIMO cellularnetwork.Then the system powerconsumption modelwas ameliorated.Based on this,an energy efficiency maximization problem with respect to base station density,transmit power,the number of base station antennas,users percelland pilotreuse factorwas obtained.Solving the problem,the optimalnetwork deployment,as wellas the relationship between the optimalvariables,hardware characteristics and propagation environmentwas obtained.Finally, simulation and numerical results show that the ultra-dense network deployment can significantly improve the energy efficiency.However,with the further increase of the density of the base station,the improvementof the energy efficiency was quick ly saturated.More interestingly,the dep loyment scenario determined by the energy efficiency optim ization was just massive MIMOscenarios.
energy efficiency,ultra-dense network,massive MIMO,multi-user MIMO,uplink
TN929.5
:A
10.11959/j.issn.1000-0801.2017068

葛亮(1993-),男,南京邮电大学通信与信息工程学院硕士生,主要研究方向为无线通信、超密集网络的能量效率分析与设计。

王志旭(1993-),男,南京邮电大学通信与信息工程学院硕士生,主要研究方向为无线通信、大规模MIMO中的导频设计与估计。
2017-01-13;
2017-03-06
