圆易错题剖析

甘肃省礼县第四中学(742200) 裴雪莲 ●

圆易错题剖析

甘肃省礼县第四中学(742200) 裴雪莲 ●

圆是初中数学教学的重点之一，也是中考的热点，因这一部分知识概念杂，公式多，在学习中易出现错误，下面从同学们平时学习中易出现错误的知识点进行举例分析，希望对同学们学习圆的相关知识有所帮助．

例1 下列命题中正确的有( )．

①经过三点可以作一个圆，②半径相等的两个半圆是等弧，③直径是弦，④三角形的内心到各边的距离相等

A．1个 B．2个 C．3个 D．4个

易错点 对圆中的基本概念(如弦、弧、圆心角、内心等)没有正确掌握．

解析 过不在同一直线上的三点才可以作一个圆，①错;半径相等的两个半圆所对的圆心角都为180°，所以所对的弧(半圆)相等，②正确;直径也是弦，③正确;三角形的内心指三角形的三个内角的角平分线的交点，该点到三边的距离相等，④正确．故选C．

例2 如图1，AB是⊙O的弦，OE⊥AB于E，交⊙O于点D，则以下说法不正确的是( )．

C．OE=DE D．∠ACB=∠AOD

易错点 不能正确运用垂径定理解决有关圆的问题．

解析 根据垂径定理知选项 A、B是正确的．又△AOB为等腰△，则．由同弧所对的圆周角等于圆心角的一半，选项D正确;垂径定理中平分的是弦，而不是半径，故C错．

易错点 对圆心角定理运用不熟练．

解析 ∵CD⊥AB，AB是直径，

例4 在平面直角坐标系中，以点(3，4)为圆心，4为半径的圆一定( )．

A．与x轴相交，与y轴相切

B．与x轴相交，与y轴相交

C．与x轴相切，与y轴相切

D．与x轴相切，与y轴相交

易错点 不能准确判断直线与圆的位置关系

解析 圆心到x轴的距离为4，所以圆与x轴相切;圆心到y轴的距离为3＜4，所以圆与y轴相交．故选D．

例5 若⊙O1的半径为6，⊙O2与⊙O1外切，圆心距O1O2=10，则⊙O2的半径为( )．

A．16 B．8个 C．4 D．4或16

易错点 对圆与圆的位置关系，以及圆心距与圆的半径的关系理解不到位．

解析 设两圆的半径分别为R和r，且R≥r，∵两圆外切，可知两圆的半径之和等于圆心距，即R+r=O1O2，∴R=O1O2－r=10－6=4．故选C．

例6 如图3在梯形ABCD中，AB∥CD，⊙O为内切圆，E为切点，求∠AOD的度数．

易错点 对与内切圆有关的概念理解不到位

解析 ∵AB∥CD，∴∠ADC+∠BAD=180°．又⊙O内切于梯形ABCD，∴OA，OD分别是∠BAD与∠ADC的角平分线

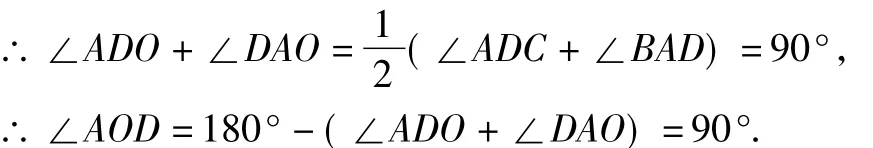
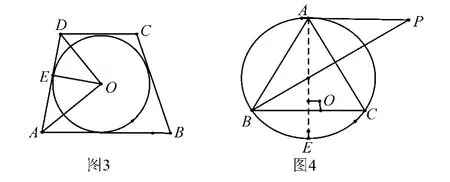
例7 如图4，⊙O是△ABC的外接圆，AB=AC，过A点作AP∥BC，交BO的延长线于点P，求证:AP是⊙O的切线．

易错点 不能运用相关知识证明一条直线是否为圆的切线．

解析 证明:过A作AE⊥BC，交BC于点E，∵AB= AC，∴BE=CE，∴点O在AE上．又AP∥BC，∴AE⊥AP，∴AP是⊙O的切线．

例8 已知两圆的圆心距为4，两圆的半径分别为方程x2－8x+15=0的两个根，则两圆的位置关系是( )．

A．外切 B．外离 C．内含 D．相交

易错点 已知圆心距与两圆的半径，不能正确探索两圆的位置关系．

解析 由x2－8x+15=0解得x1=3，x2=5．又5－3＜4＜5+3，∴两圆相交．故选D．

例9 如图5，已知⊙O的半径为R，AB是⊙O的直径，D是AB的延长线上一点，DC是⊙O的切线，C是切点，连接AC，若∠CAB=15°，求BD的长．

易错点 对切线的性质及解直角三角形的知识运用不当．

解析 连接OC，∵DC是⊙○的切线，

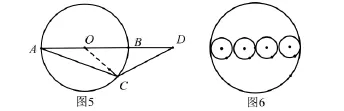
例10 已知两圆内含，且小圆的圆心在原点，半径为2，大圆的圆心为(m，0)，半径为4，求a的取值范围．

易错点 对两圆内含的性质理解不透彻．

例11 如果定义“等边扇形”为一个扇形的弧长等于它的半径长，则半径为4的等边扇形的面积是多少?

易错点 不能正确运用扇形的面积公式．

解析 设扇形的圆心角度数为 n°，则依题意有

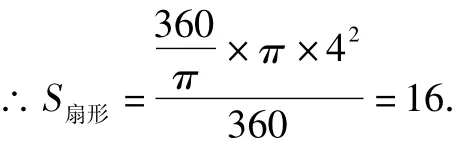
例12 已知如图6，5个圆的圆心在同一条直线上，且互相相切，若大圆的直径是20，4个小圆的大小相等，则这5个圆的周长的和为多少?

易错点 对圆的周长公式运用不熟练．

G632

B

1008－0333(2017)02－0034－02