引探教学，探究“全等”奥秘

江苏省南通市通州区四安中学(226352) 赵小锋 ●

引探教学，探究“全等”奥秘

江苏省南通市通州区四安中学(226352) 赵小锋 ●

全等三角形的知识是在线段、角、相交线、平行线以及有关三角形的知识之后出现的．教师可以通过“实物模型，形成概念”、“翻转平移，找寻规律”和“交流归纳，升华素养”等方式让学生在学习新知识的每一个环节都能够通过切身体验，动脑思考，合作探究完成，从而达到发展学生的思维能力，提升学生的学习能力的目的．

初中数学;引探教学法;教学策略

一、实物模型，形成概念

现实生活中存在许许多多形状大小相同的图形，教师可以通过贴近学生们生活的图案来激发他们探究的兴趣．通过生活元素的运用，给学生们带来亲切感，教师在引导教学的时候，效果会大为显著．

在初识全等三角形的时候，为了能让学生们在脑中形成一个新的数学概念．我通过展示实物模型的方式，让学生们认识全等的概念．在上课的时候，我拿出了三个等腰直角三角形的尺子，其中两个的型号相同，另一个偏小．我让学生们观察这三个尺子有什么相同点，有什么不同点．教师将问题抛给学生，这样他们就能多思考，在课堂上就会提高听课的注意力．在学生们思考过后，我拿着两个不同型号的等腰直角三角形的尺子进行比较，两个尺子的三个角度是对应相等的，但是尺子对应边的长度是不等的，而两个相同型号的尺子叠放在一起正好重合．通过这一点，我告诉学生们，能够完全重合的两个三角形就叫做全等三角形，小的尺子和大的尺子只能说是相似，不能说是全等．我通过实物的演示，让学生们通过观察和思考，能够理解全等三角形的概念．

教师通过几分钟借助实物的讲解，比单纯的让学生们空想的方式更加真实有效，学生们在这种教学方式下，会增加对新知识的兴趣，这对之后更进一步的学习有很大的帮助．

二、翻转平移，找寻规律

有时候题目中的全等三角形经过平移、翻折或者旋转的变化，学生们不容易观察出对应的条件，所以教师应该加强这方面的教学．学生们经过基本的学习，可以巩固对新知识的掌握情况，对学生们在一些情况下确定全等三角形的对应元素有很大的帮助．

我通过多媒体来演示平移、翻折、旋转这三种变换．在观看的同时，我让学生们思考图形的位置发生了变化，前后两个三角形是否全等．平移的情况对于学生们没有难度，在进行翻折和旋转演示的时候，我让学生们在图中找出对应顶点、对应角和对应边．我让学生们先找到对应的顶点，然后通过将顶点联系起来找到连接两个顶点的边，这样就可以不被位置变化的三角形迷惑了．为了能让学生们更好地理解，我让他们自己制作两个全等的三角形，通过自己亲手尝试图形全等变换的过程，进而让学生们理解图形变换的本质．在学生们学习了简单的变换之后，我给学生们两个有重叠部分的三角形，它是经过翻折和旋转得到的，如上图．此时我让学生们大胆地去进行标记相应的元素，首先△ACD和△BDC，共用一个边CD，这时通过对比角A和角B相等，边AC和边BD相等，边AD和BC是相等的，通过将条件对比，可以得到△ACD和△BDC是全等的三角形．在多媒体的辅助下，学生们可以一步一步地观察到图形的变化．学生从根本上了解了图形是如何变化的，在以后遇到复杂的证明题的时候，他们就有基本的思路去找对应的条件．

三、交流归纳，升华素养

在学生们基本掌握了全等三角形的概念后，教师可以通过让学生们相互交流然后去归纳出来证明全等三角形的定理．学生们通过观察全等三角形对应边和对应角的关系，在教师的引导下，对所学的知识进行总结．

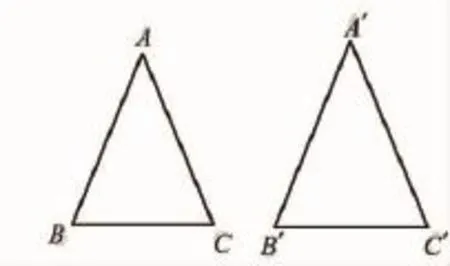
在学习证明全等三角形的定理时，我在黑板上画出两个全等三角形，让学生们去总结出怎么用角和边的关系来证明这两个三角形是全等的．同学们指出三个角对应相等，三个边对应相等．此时我说三个边对应相等就可以去证明，如果三个边对应相等后，它们组合成的三角形的角度肯定是一样的，因为用相同长度的线段组成三角形只有一种情况．然后我让学生们在纸上画两个全等三角形，确定角B的度数，然后让学生们一起讨论，增加两个什么条件就可以去证明全等三角形．学生们讨论得非常激烈，通过在纸上尝试，慢慢的学生们找到了相应的条件．有学生说，确定了角A的度数和AB的长度，有学生说，确定了AB和BC的长度，有学生说，确定角A的度数和BC的长度．这三个情况都可以证明全等，学生们通过相互之间的讨论合作，归纳出来了判定两个三角形是全等三角形的定理，即SSS、SAS、ASA、AAS．学生们在老师的引导下可以去探索数学知识，这是对他们在课堂的主体地位的体现，学生们通过自己的努力去理解新知识，这样的教学模式对于提高学生们学习兴趣有很大的帮助．

理想的课堂是教师作为引路人，学生通过自己的努力探索找寻新知识．学生们在进行小组讨论的过程中，各异的思维进行碰撞，这样的方式能加深学生对新知识的理解．在归纳的时候，也是学生们自我获取知识的提升．

教师通过对教学设计进行优化，提高学生的参与度．在学习新知识的每一个环节都能够让学生通过切身体验，动脑思考，合作探究完成，从而达到发展学生的思维能力，提升学生的学习能力的目的．

［1］梅少琳，杨雪莲．介绍全等三角形的判定定理的探究式教学［J］．中小学数学(初中版)，2010(4)．

［2］王修燕．探究中引领，研讨中发展［J］．初中数学教与学，2011(2)．

G632

B

1008－0333(2017)02－0048－01