源自课本 有效改编——2015年泰州市中考数学第25题的思考

江苏省兴化市昌荣中心校(225734) 丁 冬 ●

源自课本 有效改编
——2015年泰州市中考数学第25题的思考

江苏省兴化市昌荣中心校(225734) 丁 冬 ●

近年来，各地一些中考数学命题的素材来源于课本例题、习题的改编，对于考查数学知识、方法、能力有其合理性、创新性．2015年泰州市中考数学第25题源自苏科版数学八年级教材的例题改编，体现了根在书中的特色，同时也有清新之感．研读这道题，笔者对此题有一些思考和见解．

课本例题;改编;中考试题;方法多元化;正方形;定点;最小值

纵观近年来，全国许多地区中考数学试卷中的部分试题命制源自课本例题、习题的改编，既让考生有似曾相识的感觉，又有一种清新之感．俗话说“为有源头活水来”，取材于课本的同时，对题目的条件或结论进行别具匠心的重构打磨、引申挖掘，既让考题绽放华彩，又能有效考查不同层次学生的数学知识和能力．2015年泰州市中考数学第25题，这道题便是源自苏科版数学八年级教材．以下是笔者对于2015年泰州市中考数学第25题的一些思考和见解．

一、原题呈现

(源于苏科版数学八年级下册第82页的例5)

已知:如图1，在正方形 ABCD中，点A'、B'、C'、D'分别在AB、BC、CD、DA上，且AA'=BB'=CC'=DD'．求证:四边形A'B'C'D'是正方形．

分析 要证明一个四边形是正方形，通常有两种思路，即先证菱形，进而再得正方形;或先证矩形，进而再得正方形，具体问题解决时，须根据题目条件，选用合适的方法予以证明．

证法1 ∵四边形ABCD是正方形，

∴四边形A'B'C'D'是菱形(四边相等的四边形是菱形)．

由△AA'D'≌△BB'A'，可得∠2=∠3．

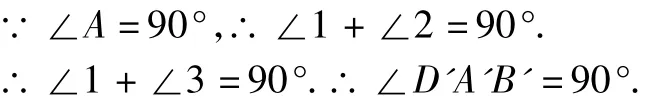
∴菱形A'B'C'D'是正方形(有一个角是直角的菱形是正方形)．

证法2 易证△AA'D'≌△BB'A'，∴∠2=∠3，D'A' =A'B'．

同理可证∠A'B'C'=∠B'C'D'=90°，

∴四边形A'B'C'D'是矩形(三个角是直角的四边形是矩形)．

又∵D'A'=A'B'，∴矩形A'B'C'D'是正方形(有一组邻边相等的矩形是正方形)．

二、改编创新

(2015年泰州市中考数学第25题)如图2，正方形 ABCD的边长为8cm，E、F、G、H分别是AB、BC、CD、DA上的动点，且AE=BF=CG=DH．

(1)求证:四边形 EFGH是正方形;

(2)判断直线EG是否经过一个定点，并说明理由;

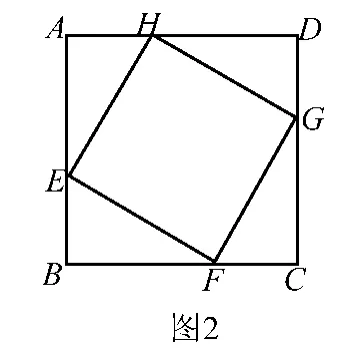
(3)求四边形EFGH面积的最小值．

仔细看这道中考题，题目条件及第(1)问与课本原题基本一致，只稍作添加了正方形的边长为8cm这一数据;第(2)、(3)两问则是有效地改编与创新，其中动直线经过定点、最值问题对于考查不同层次学生的数学思维和能力，有较好的区分度．

分析 第(1)问可先证△AEH≌△BFE≌△CGF≌△DHG，得出四边形EFGH是菱形(或矩形)，再根据“有一个角是直角的菱形是正方形”(或“有一组邻边相等的矩形是正方形”)证得四边形EFGH是正方形．

第(2)问的解法不唯一，既可采用几何证法，证明出四边形AECG是平行四边形，再根据点O是对角线的交点，同时也是它们两条对角线的中点即可得证;也可通过建立直角坐标系，运用解析法来解决．

第(3)问通过建立二次函数的模型，将几何问题代数化来解决．

三、解法探究

解 (1)证法同上面“原题呈现”中的两种证法．

(2)解法1 如图3，连接AC、EG相交于点O．

∵AE=CG，AE∥CG，∴四边形AECG是平行四边形．

∴点O为对角线AC的中点．

即直线EG经过定点，且定点为对角线AC的中点O．

解法2 如图4，以点B为坐标原点，线段BC、BA所在直线分别为x轴、y轴建立直角坐标系．

设BE=acm(0≤a≤8)，则DG=acm．

设直线EG的表达式为y=kx+b．

将E(0，a)，G(8，8－a)代入，

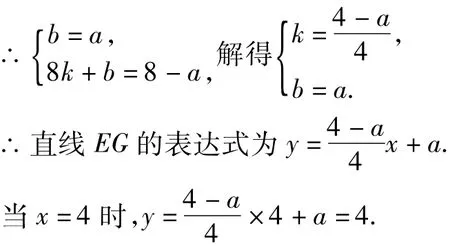
∴直线EG经过定点(4，4)．

又∵A(0，8)，C(8，0)．

∴AC的中点坐标为(4，4)．

∴直线EG经过定点，且定点为AC的中点．

(3)解法1 设AE=xcm，则AH=(8－x)cm．

∴当x=4时，四边形EFGH面积的最小值为32．

解法2 设AE=xcm，则AH=(8－x)cm．

在Rt△AEH中，由勾股定理，知AE2+AH2=EH2，

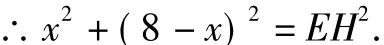
即EH2=2x2－16x+64．

又∵四边形EFGH为正方形，

∴S正方形EFGH=EH2=2x2－16x+64=2(x－4)2+32．

∴当x=4时，四边形EFGH面积的最小值为32．

解法3 ∵△AEH≌△BFE≌△CGF≌△DHG，且正方形ABCD的面积始终为64，

∴要使四边形EFGH面积的最小，只要△AEH的面积最大即可．

∴当x=4时，△AEH的面积最大值为8．

∴ S正方形EFGH=S正方形ABCD－4S△AEH=64－4×8=32．

∴四边形EFGH面积的最小值为32．

四、几点思考

1．注重课本例题、习题的教学，切忌舍本逐末，抛弃课本教材，一味求深求难．同时依据课标、考纲要求，对课本例题、习题适当改编、挖掘一些变式题、拓展题，逐步训练学生的数学思维，渗透数学思想和解题技巧．

2．注重通性通法，同时提倡解题方法的优化．几何问题有时并不拘泥于只用几何方法来解决．思维的发散、方法的多元化，为积累解题经验、提高解题能力，有着积极意义．

3．中考数学的复习，注重回归课本，梳理知识，把握知识的前后关联．同时，研究本地区近年来中考数学试题的特色，对长效考点、考题做到心中有数，有的放矢．

G632

B

1008－0333(2017)02－0033－02