最小二乘叠前深度偏移成像理论与方法

王华忠,胡江涛,2,郭 颂

(1.波现象与反演成像研究组(WPI),同济大学海洋与地球科学学院,上海200092;2.油气藏地质及开发工程国家重点实验室,成都理工大学,四川成都610059)



最小二乘叠前深度偏移成像理论与方法

王华忠1,胡江涛1,2,郭 颂1

(1.波现象与反演成像研究组(WPI),同济大学海洋与地球科学学院,上海200092;2.油气藏地质及开发工程国家重点实验室,成都理工大学,四川成都610059)

地震波成像的目的首先是定位反射界面或散射点的空间位置,描述地下地质体的几何结构;然后是估计地下介质的物性参数,主要是与速度和密度相关的参数;最终是与岩石物理结合描述含油气储层。以地震波传播的散射场表达以及逆散射成像为切入点,首先给出散射波的表达形式,讨论了逆散射成像的本质与逆散射成像所需要的叠前地震观测数据及对应的观测方式;然后给出一般的线性化最小二乘叠前深度偏移(Least-squares Prestack Depth Migration,LS_PSDM)基本理论框架,只要能给出用Green函数计算的波传播算子,就可以实现线性化的LS_PSDM;接着讨论了当前广受关注的最小二乘逆时深度偏移(Least-squares Reverse Time Migration,LS_RTM)方法,给出了最小二乘偏移成像的迭代实现方法和保反射界面结构的总变差正则化方法以及数值结果;最后分析了基于反射波估计反射系数的成像方法和基于散射波估计散射强度的成像方法的差异,指出针对勘探地震介质特征和波场特征的成像方法是最具实用性的方法,逆散射成像应该在此基础上进行。基于散射波的成像方法能否满足储层描述的要求,有待进一步研究工作的检验。

散射场表达;逆散射成像;反射波成像;最小二乘叠前深度偏移;全波形反演

油气勘探地震学的最终目标是储层描述。实现储层描述与刻画的途径有两条，一是常规的、基于反射波场的保幅或保真角度反射系数的成像。该方法基于保真的角度成像道集,利用1D波阻抗反演和/或AVA叠前反演得到弹性参数,与岩石物理、测井结合,进行储层识别和描述,是目前常用的从地震成像走向储层刻画的方法技术体系[1]。该技术体系的核心包括三方面的关键因素:①满足速度估计和保真成像要求的数据体;②较准确的背景速度模型建立技术和保真角度反射系数成像技术;③基于保真成像道集的储层参数估计及储层描述方法。实现储层描述与刻画的另一条途径是当前石油工业界十分关注的全波形反演(Full Waveform Inversion,FWI)成像——基于散射和逆散射的反演成像技术,它的本质目标是估计宽(全)波数带的弹性参数场,基于此反演结果直接进行储层描述。但该方法仅仅利用地表观测的有限带宽、有限孔径和无假频数据,其实用化并不成功,仅仅在低频和长偏移距地表观测数据情况下能得到背景速度的估计,弹性参数跃变(高波数)成分的估计仍然采用最小二乘RTM。然而,依赖散(反)射波振幅的LS_RTM也很难有效地收敛并给出满足储层描述要求的反演成像结果。

在一些数学家看来,石油地震勘探问题很简单,就是用波动方程作为实测数据预测器,若基于一个假设的参数模型求解波动方程得到的合成数据与实测叠前地震数据的总误差最小,则该假设模型就是所求的地下岩石弹性参数估计结果。事实上,这完全低估了勘探地震中弹性参数反演问题的复杂性[2-3]。从勘探地震学出现伊始,勘探地震学家走的就是一条实际问题驱动的路线:针对成像问题,先由CMP道集估计背景初始速度,进行叠后偏移成像;然后进入叠前偏移成像,由成像道集进行偏移速度分析,或进行层析成像建立速度模型。迭代进行叠前偏移成像和速度模型的更新是石油工业界发展出的实用化地震波成像路线,经实践检验是行之有效的。更细致的能用于储层描述的参数估计是基于1D波阻抗反演和/或AVA角度道集反演[4]。事实上,一直有很多学者在探讨是否能从更数学化的角度来解决成像问题,并且分成两条路线,一条是以BLEISTEIN为代表的基于反射波的线性反演路线[5-6];另一条是以TARANTOLA为代表的基于散射波的全波形拟合非线性反演路线[7]。前者是当前勘探地震反射波成像的完整理论框架,一直在指导反射波成像的具体实践,取得了很好的应用效果；后者是最近几年勘探地震中的热点研究问题,利用低频透射波估计背景速度在合适的探区获得了比较显著的应用效果,但以LS_RTM为代表的弹性参数高波数扰动量的估计还没有看到具体的实用效果。

基于此,本文以地震波传播的散射场表达与逆散射成像的本质为切入点,讨论了一般意义下叠前偏移成像与逆散射成像之间的区别与联系,重点分析了最小二乘叠前深度偏移成像方法存在的问题,认为勘探地震中的地震波成像要充分考虑地下介质以分层沉积为主的特点以及波在这样的介质中传播以反射波为主的特点构建合适的成像方法技术,而不是完全基于地下介质是背景+散射的模式构建逆散射成像技术。在方位角度反射系数估计结果比较准确的基础上再进行逆散射成像应该是LS_RTM方法走向实用化的合理路线。

1 地震波传播的散射场表达

FWI和波动理论地震波层析成像本质上是针对地下介质为背景+散射体情形的,因此,散射体引起的散射场的表达是其中最基本的问题。

1.1 基本的声波方程和声散射势的引入

1.1.1 基本的声波方程

一般地,我们假设波在地下介质中的传播可以由如下声波方程控制:

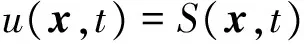
(1)

式中:u(x,t)为声场势,它是时间t∈R和空间坐标x∈Ω⊆R的函数;v(x)代表速度场;ρ(x)代表密度场;S(x,t)代表体积场源。

在频率-空间域,上式变为:

(2a)

其中,

(2b)

为声波传播算子。

定义背景介质中的声波传播满足如下方程:

(3a)

其中,

(3b)

为背景介质中的声波传播算子。

1.1.2 声散射势的引入

根据(2)式和(3)式,定义声散射势为:

Va(x,ω)=La(x,ω)-La0(x,ω)

(4)

其中,

(5a)

(5b)

1.2 标量波方程和标量波散射势的引入

勘探地震学很多情况下关注标量波方程(或密度不变情况下的声波方程)。频率-空间域标量波方程形式为:

(6a)

其中,

(6b)

为标量波传播算子。

定义背景介质中的声波传播满足如下方程:

(7a)

其中,

(7b)

为背景介质中的标量波传播算子。

根据(6)式和(7)式,定义标量波散射势为:

(8a)

其中,

(8b)

称为散射强度。(8a)式定义的散射势在速度扰动不大时还可以写为如下形式:

(9)

上述形式引入δv(x)=v(x)-v0(x),更清楚地反映出速度的局部变化是散射势的本质。从散射势的定义也可以看出,估计散射强度的绕(散)射波动理论层析成像与估计(或定位)反射系数的叠前偏移成像是有严格区别的。根据(9)式定义的散射势,可以写出散射势引起的场的传播控制方程:

(10)

求解该方程可以得到散射势引起的场us(x,ω),进而进行波动理论的层析成像。这就是在一定的反演理论下的线性化散射波FWI(LS_RTM)的正问题基础。

1.3Lippmann-Schwinger方程的导出及散射场的具体表达

L=L0+L0VL

(11)

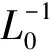
假如波传播算子L用Green函数G表示,(11)式可以重写为:

G=G0+G0VG

(12)

(12)式是非线性的,它能被进一步重写为:

(13)

对(13)式右端项进行如下的级数展开,得:

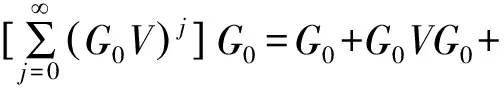
G0VG0VG0+G0VG0VG0VG0+…

(14)

(12)式和(14)式被称为Lippmann-Schwinger方程[8-9]。

很显然,假如j≤2,(14)式就仅描述一个忽略了二阶以上散射波的波传播过程。即线性化的波传播算子仅仅描述波传播过程中的一阶散射，也就是:

G≈G0+G0VG0

(15)

(15)式就是Born近似下的波传播算子。其中方程右端的第一项描述了背景场中的波传播现象,第二项描述了一阶散射波的传播现象。(12)至(15)式清楚地说明了Born近似的物理含义,只有当散射势比较弱时,(14)式中高于二阶的项才可以被忽略不计。从(14)式可以清楚地看出,高阶散射场能否被忽略,除了散射势比较弱的条件外,散射体的体积也很重要,因为散射场是散射势的体积积分结果。小散射体和弱散射势是Born近似成立的条件。

从(15)式可以看出,Born近似线性化算子模拟出的总波场包括两部分:第一部分是由背景Green函数所描述的背景波场;第二部分是由散射势引起的、方程(14)中的第二项所描述的散射场。很显然,这里存在一个背景速度场如何获取才能得到符合Born近似要求的背景场的问题，原则上的要求是入射场中不能存在散射场成分。事实上,在特别复杂、变化特别剧烈的速度场中,一阶Born近似的应用效果是很值得考虑的。这也是人们逐步在考虑引入更高阶的Born近似、降低一阶Born近似弱散射要求的原因。但这样做也会引入高阶散射场计算上的复杂性。

假定Born近似假设成立,根据(15)式,线性化的总波场可以写成

(16)

其中,Born近似后的散射波场记为:

(17)

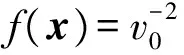
Born近似的物理实质是:在背景场u0(ξ,η,ω)中没有散射场;在扰动场中,只存在一次散射场。尽管用这种方式描述的波传播与实际的波传播不同,但当二阶及二阶以上的散射场能量比较弱时,用Born近似散射场进行最小二乘叠前深度偏移、估计散射强度还是比较有效的。这是当前最小二乘叠前深度偏移成像的基础,也预示着未来的最小二乘叠前深度偏移成像需要考虑更高阶次的散射波才能得到更好的结果[10]。

关于子波问题,可以认为已经包含在背景场u0(x,η,ω)中,也可以用G0(x,η,ω)S(ω)来表示,其中S(ω)代表子波的谱。但是,在最小二乘叠前深度偏移成像中,假设子波已知,仅需估计散射强度。事实上,子波的振幅谱和相位谱不正确都会影响散射强度估计的精度。因此,子波研究是决定最小二乘叠前深度偏移反演成像结果好坏的重要因素。

2 逆散射问题分析

2.1 常速背景介质与平面波入射情形下散射场与散射势间的关系

首先给出常速介质中自由空间Green函数:

(18)

式中:x代表场点位置，x′代表散射源点位置，|x-x′|代表源点与场点之间的距离;k代表场的波数。将(18)式代入(17)式定义的散射场中,得:

(19)

一般地,在远场近似假设下,入射场在常速介质中传播可以用平面波近似:

(20)

式中:s0是平面波入射方向的单位矢量。将(20)式代入(19)式得:

(21)

(21)式描述的波的传播关系如图1所示。由(16)式知,此时总场可表示为:

(22)

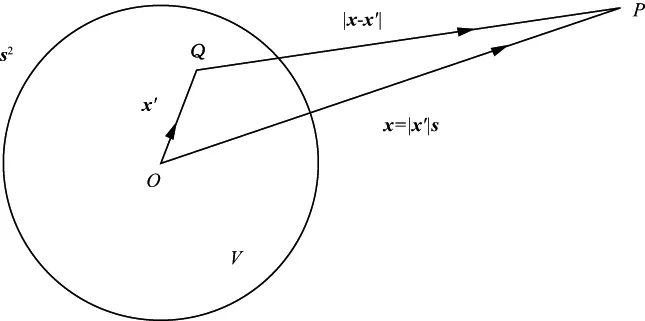
图1 空间局部散射体引起的散射波传播关系

由图1可知,当场点P距离散射体比较远,散射体积源分布空间V有限时,用Q代表散射体积源内的点,O代表坐标原点,则可以做如下近似推导:

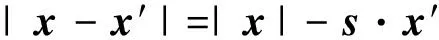
(23)

(24)

式中:s是散射波传播的局部平面波方向的单位矢量。将(24)式代入(22)式,得:

(25)

其中,

(26)

称为散射波方向谱。定义散射势的Fourier变换为:

(27)

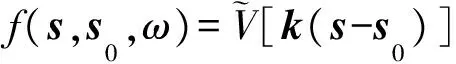
据此,可以总结出如下定理:在Born近似下,相对于散射体的远场区域,散射势的Fourier变换等于散射波方向谱,且有关系式

(28)

成立[11]。

由此可知,在常速介质情况下,所谓逆散射问题就是根据散射波方向谱确定散射势的Fourier分量。散射势的所有Fourier分量都确定后,通过Fourier逆变换就可以完全精确地恢复散射势。

上述定理尽管是在平面波入射和常速背景情况下得到的,但其理论指导意义十分明显。从k′的表达式中可以看出,确定k′的低波数部分需要大角度散射波和低频数据;确定k′的高波数部分需要小角度散射波和高频数据。总之,震源子波的频带范围、观测系统和背景速度场的分布决定了散射强度估计结果的分辨率。因此,宽带、宽方位观测数据是高精度反演成像所必需的。尽管(28)式中没有明确体现,无假频的高密度观测也是必要的。

2.2 高频近似下的Born近似的物理含义

Born近似下的散射场(17)式也可以表示为:

(29)

用渐进Green函数(即Green函数的WKBJ近似解)代入上式,得:

us(ξ,η,ω)=ω2∫dxf(x)A(x,η)A(ξ,x)·

exp{-iω[T(x,η)+T(ξ,x)]}

(30)

在散射点周围,对旅行时进行线性化,即围绕中心射线进行Taylor展开:

(31)

式中:p(x0,x′)表示旅行时场T(x,x′)在点x0处的一阶导数,其方向为中心射线的切线方向。因此,(30)式中的指数部分可以化为:

(32)

其中,

(33)

代表波场的一种波数关系[12]。其几何意义如图2所示。

图2 地震波传播过程中波矢量在反射点处的几何关系

图2中p=ω[p(x0,η)+p(x0,ξ)]=2ncosθ/v0(x0)。其中n为界面的外法线方向单位向量;θ为射线的入射角;v0(x0)为x0处的背景速度。根据图2 所示几何关系有:

(34)

注意(34)式与(28)式的一致性,但这是从反射的角度来解释。从k的表达式中可以看出,确定k的低波数部分需要大角度散射波和低频数据,确定k的高波数部分要小角度散射波和高频数据。同样地,此处希望满足k规定的谱的完整性。这进一步证明了高精度的逆散射反演成像需要宽频带和宽方位的地震数据观测。

3 Bayes框架下基于Born近似散射场的散射势估计方法

(17)式定义了一个Fredholm第一类积分方程,它描述的是一个线性问题。此处,我们将该Fredholm第一类积分方程的求解转化为一个Bayes估计问题,就是将线性问题的求解转化为利用泛函变分求极值的问题。基本内容表述如下。

假设(17)式定义的积分方程写成算子表达形式:

Km=d

(35)

式中:K是Fredholm第一类积分方程的积分核。由(17)式知,积分核的定义为:

K[v0(x),x,ω]=ω2G0(ξ,x,ω)u0(x,η,ω)

(36)

式中:m代表由f(x)作为元素形成的矢量;d代表每个炮检点对应的地震道的频谱值。K:H1→H2被认为是一个有界的线性算子,定义如下Tikhonov泛函:

(37)

对(37)式求解的首要问题是计算泛函关于参数变化的导数,即泛函的梯度。为此,利用如下的变分方法。

对于任意的介质扰动δm∈H1和扰动步长τ∈R,总存在如下的泛函变分:

(38)

对(38)式定义的变分求偏导数,即:

=[(〈Km-d,Kδm〉H2+α〈m,δm〉H1)+

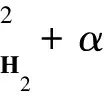
=(〈Km-d,Kδm〉H2+α〈m,δm〉H1)

=[〈K*(Km-d),δm〉H1+α〈m,δm〉H1]

=〈K*(Km-d)+αm,δm〉H1

=〈(K*K+αI)m-K*d,δm〉H1

=〈GradI(m),δm〉H1

(39)

其中,

(40)

是误差泛函相对于参数模型的梯度。K*是波场正传播算子的共轭算子,代表波场的反传播。经典地,我们利用该梯度构造最速下降迭代方法求解Born近似后的线性问题的解。迭代格式为:

(41)

其中,μk为第k个迭代步长。当然,更一般性的解法是令(40)式定义的梯度等于0,得到如下线性系统的法方程:

(42)

法方程的求解一般用共轭梯度方法。但是,由于勘探地震中模型参数描述采用网格化方式,而模型参数个数非常多,(42)式右端的Hessian矩阵异常庞大。若用NX×NY×NZ表示要估计的模型参数的个数,那么Hessian矩阵的规模为(NX×NY×NZ)×(NX×NY×NZ),当前的计算机技术还不能满足如此巨大规模的线性方程组的求解。再者,形成Hessian矩阵本身也是一个巨大的挑战。所以,当前解法方程、进行最小二乘偏移成像的基本做法是先进行常规的叠前深度偏移成像,然后用对角矩阵元素(地震波照明能量)对成像叠加后的结果进行照明补偿,就是用Hessian矩阵的对角元素去除成像结果。也可以用角度Hessian矩阵的对角元素去除每个共角度成像剖面,然后进行叠加,生成最终剖面。当然,也可以不叠加,产生照明补偿后的角度成像道集。(42)式代表的问题可以认为是图像反褶积问题。右端项是常规偏移成像得到的结果,它是模糊的图像。用共轭梯度法解(42)式相当于图像去模糊运算,可以显著地提高最终图像的质量。求解(42)式最关键的问题是难以形成Hessian矩阵,根据Hessian矩阵元素的物理含义(相邻空间点Green函数的互相关),学者们提出了很多简化的Hessian矩阵生成方法。

实质上,(40)式计算的梯度不会等于0,因为正演数据和实测数据的残差永远不会等于0。这是最小二乘偏移成像中迭代解法占主要地位的根本原因。迭代法涉及残差计算rk+1=Kmk-dobs,这需要一步反偏移;(41)式中的K*rk+1=K*(Kmk-dobs)代表一迭代步中残差的反向传播,需要一步残差的反向传播。同时,迭代法要考虑步长的计算并用Hessian矩阵的逆对梯度项进行预条件处理。以上只是一步迭代需要的计算量,最小二乘偏移成像一般需要n步迭代计算,因此,迭代法的计算量也很大。

迭代的线性最小二乘反演方法中并不更新核函数,因为我们假定核函数K[v0(x),x,ω]仅仅与背景速度v0(x)有关。但这仅仅是从计算效率方面考虑的结果,本质上还是应该更新核函数,因为背景速度与扰动速度是相互耦合的。存在较强多次散射波(反射波)时,要么事先消除多次波,要么构建非线性的最小二乘反演成像方法。

(41)式或(42)式中计算出的m(x)代表速度的一种相对变化,只有在速度跃变的界面或绕射点处才会出现,因此,它反映了速度场中的高频变化部分。这部分高波数速度扰动可以用来代表界面位置和绕射位置的图像,与一般的叠前深度偏移类似。也可以精确估计这部分高波数速度扰动,用来刻画储层的性质。但是,我们认为,只有提供满足(28)式或(34)式要求的叠前数据体时,反演成像的结果才比较可靠,才可以用来进行有效的储层解释。目前,仅仅利用地表观测的反射(散射)波场,加上噪声的存在,m(x)的估计结果很难满足精确描述储层的要求。线性的最小二乘反演成像可以认为是背景速度正确时的反(散)射波FWI。因此,目前的FWI要得到适用于储层解释的反演结果也是不现实的。速度(更应该是波阻抗)跃变的精确估计是一个比背景速度估计更难的问题。

需要指出的是,本节讨论的内容适用于利用各种波传播算子(包括Kirchhoff积分算子、Gauss-Beam算子、单向波传播算子以及双向波传播算子)计算Green函数,进行线性化的最小二乘叠前深度偏移成像。

4 线性与非线性最小二乘逆时深度偏移(LS_RTM)

FWI的本质目的是估计宽或全波数带的速度(最好是波阻抗)。但是当前勘探地震数据采集并没有按(28)式或(34)式的要求进行,而是仅仅在地表进行有限带宽和有限孔径的观测。这是当前FWI分成估计低波数背景速度和高波数速度扰动两部分的主要原因。FWI背景速度估计主要是利用低频长偏移距的透射波;FWI速度扰动的估计是在假设背景速度正确的基础上利用反(散)射波进行的。速度(或波阻抗)扰动的估计必须利用反(散)射波的振幅信息,基于目前的数据采集,它们的估计精度更难以保障。基于振幅的高波数弹性参数的估计是更困难的问题。目前进行速度(或波阻抗)扰动估计的主要技术是线性或非线性的最小二乘逆时深度偏移方法。

4.1 非线性的LS_RTM

我们首先列出非线性的最小二乘逆时深度偏移成像(LS_RTM)公式。正向波场外推方程为:

(43a)

式中:fb(Ω,t)代表边界条件,一般用PML边界条件,Ω代表计算波场在空间上的边界。

反向波场外推方程为:

(43b)

式中:η代表观测点坐标值,uobs(η,t)代表观测点处的实测波场,ucal(η,t)代表观测点处的正演合成波场。FWI进行波场残差外推时,仅有观测点处有波场残差,因此有(43b)这样的边界条件的定义。实际上,波场逆时外推并不限于这样的边界条件。

由此可见,(43a)式是一个初值问题,沿时间正向外推计算;(43b)式是一个边值问题,逆时间反向外推计算。

误差泛函梯度公式为:

(44)

式中:ξ代表不同的炮点位置;η代表不同的检波点位置。假定初始背景速度mB是已知的，δm代表要估计的高波数速度扰动量;δmB代表要估计的背景速度的扰动量。对应的迭代公式为:

(45a)

(45b)

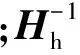
与前述基于一阶Born近似公式导出的LS_PSDM相比，非线性LS_RTM(或散/反射波FWI)的梯度项中包含了对所有波现象的预测。当背景速度不准时,不能预测的波现象会干扰梯度的计算,导致收敛慢,甚至不收敛的情况发生。比较而言,一阶Born近似仅仅考虑一次散射波的预测,梯度计算相对要更准确,因此LS_PSDM的收敛性更好。但LS_PSDM要求ucal(η,t)中仅仅包含一次散射(反射)波场,必须对实测数据uobs(η,t)做很好的预处理,尽可能使其仅保留一次散射波场。

非线性LS_RTM的计算步骤如下:

1) 给定较准确的背景偏移速度mB;

2) 计算波场ucal(η,t)和波场残差r(η,t),并产生照明矩阵(即Hessian矩阵的对角阵);

3) 计算梯度g[δm(x),δmB(x),mB(x)],并给出RTM成像结果,当成像道集拉平或数据拟合差达到要求时,迭代停止;

4) 分离梯度g[δm(x),δmB(x),mB(x)]为gh[δm(x),δmB(x),mB(x)]和gl[δm(x),δmB(x),mB(x)];

5) 考虑梯度预条件和步长,利用(45)式得到δm和δmB当前步的修正量;

6) 修改模型m(x)=mB(x)+δmB(x)+δm(x);

7) 当修正量的范数‖δm‖和‖δmB‖小于预设值时计算结束,或返回步骤2)。

从上述步骤可以看出,非线性LS_RTM包含了速度扰动量的反演和背景扰动量的反演两种成分,这两种成分的联合反演是目前地震波反演的导向性思想。

4.2 基于Born线性近似的LS_RTM

4.2.1 基于Born线性近似的LS_RTM方法

目前关于LS_RTM的讨论主要基于(16)式,我们称之为线性化的LS_RTM。为估计散射强度,定义如下误差泛函:

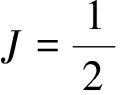
(46)

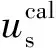
目标泛函的梯度是构造最速下降法的核心,其定义为:

(47)

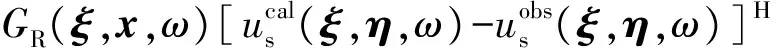
利用(47)式定义的梯度,可以进行最速下降法的最小二乘偏移成像计算:

(48)

为了加速收敛,可以用Hessian矩阵的逆对梯度方向进行预条件处理。Hessian矩阵定义为:

(49)

该Hessian矩阵是由背景介质中的Green函数规定的,其中并不包括高阶反射/绕射效应,即不包括非线性部分。双向波计算Green函数时可以包含这部分的作用。由Hessian矩阵的逆对梯度方向进行预条件处理后,最速下降法的迭代公式变为:

(50)

迭代步长μ(k)可以采用试探的方式确定,一般采用试探加抛物拟合的方法来选取最优下降步长,保证误差的下降。

迭代的每一步需要在更新后对模型进行一次反偏移,然后将反偏移得到的正演数据从原始数据中减去,判断误差是否达到要求,迭代是否终止。实质上,用反偏移来产生与实测波场逼近的波场这个过程存在太多的问题。

具体的计算步骤为:

1) 给定偏移速度场vmig(x);

4) 用残差波场进行RTM,同时产生照明矩阵;

5) 用(50)式计算迭代成像结果;

6) 进行RTM;

7) 转步骤3)。

步骤3)也可以是解法方程。但是,形成法方程本身就需要巨大的计算量,解法方程也需要大量的内存空间和计算量。解法方程的优点是正则化和预条件的方法比较多。可以看出,此处的梯度计算和波场残差计算在理论上是不够严谨的。

4.2.2 数值结果

图3展示了用公式(50)计算的声介质最小二乘反射波叠前偏移成像结果。可以看出,最小二乘偏移补偿了照明不足,提高了成像的分辨率,使成像结果的横向一致性更好,更有利于后续的储层解释。

图4对比了声介质和粘声介质下最小二乘叠前深度偏移结果,以及Tikhonov正则化和加权正则化情形下迭代最小二乘叠前深度偏移结果。可以看出,最后的粘声介质迭代20次的加权正则化叠前深度偏移结果与真实模型的反射系数很接近[13]。理论上讲,如此高分辨率和高保真的叠前深度成像结果完全满足岩性油气藏的精细刻画要求。但我们称上述数值试验及结果是一个反演骗局。对实际数据而言,成像结果远不会如此理想,具体原因包括:①地震波正演不能很好地模拟实际观测数据;②预测误差不是高斯分布的;③子波是未知的;④背景速度没有满足线性反演的要求;⑤观测数据不完整(有限孔径、不规则等);⑥影响振幅的因素复杂等。本质上,线性化的LS_RTM是Born近似条件成立时的FWI。在当前实际地震数据状况下,用这样的方式估计高波数参数扰动量的真实值,其估计精度很难评价。

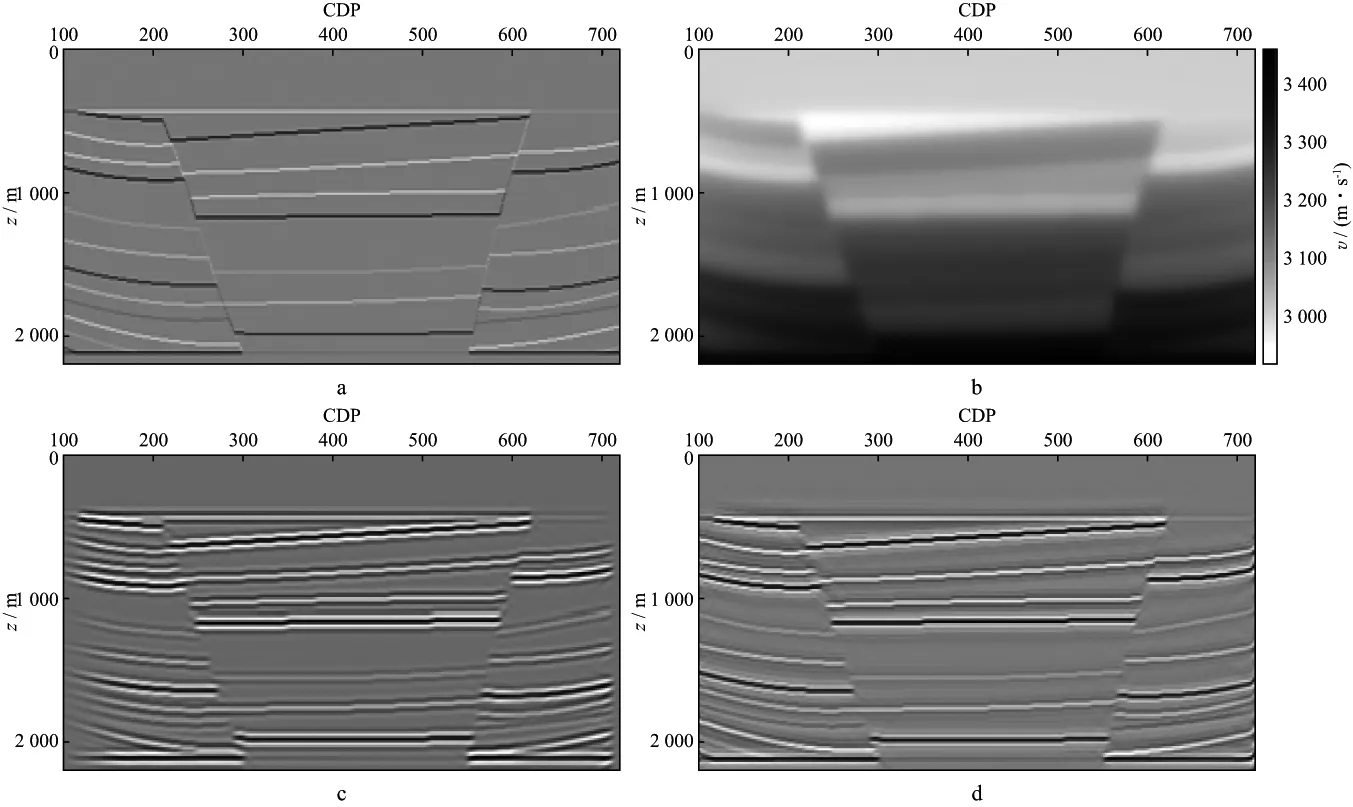
图3 声介质迭代法最小二乘叠前深度偏移结果对比a 理论反射系数; b 背景速度模型; c 常规叠前深度偏移结果; d 最小二乘叠前深度偏移结果

图4 粘声介质最小二乘叠前深度偏移结果对比a 背景速度模型; b 品质因子模型; c 声介质中模拟的单炮道集; d 粘声介质中模拟的单炮道集; e 粘声介质数据进行声介质最小二乘叠前深度偏移的结果; f 粘声介质数据进行粘声介质最小二乘叠前深度偏移的结果; g 一般Tikhonov正则化情况下的粘声介质最小二乘叠前深度偏移结果; h 加权正则化最小二乘叠前深度偏移结果

4.2.3 总变差(TV)正则化约束下的LS_RTM

对于实际数据而言,多重因素的制约使得最小二乘反演成像成为一个不适定的反问题。譬如:输入的叠前数据中包含噪声(非一次反射波)、不准确的背景速度、正演(偏移)算子不能很好地模拟波现象、子波未知等因素会影响最小二乘反演成像迭代过程中的数据匹配,使不准确的数据残差反投影并混叠在梯度中,进而影响最小二乘反演成像的收敛率。正则化是使不适定(非线性较强或凸性差)的地球物理反问题的解更稳定、更有地质意义的一类方法。常用的Tikhonov正则化可以提升反问题解的稳定性,但这种正则化方法基于L2模,得到的是一光滑解,而我们所期望得到的是“棱角”更为分明的成像剖面,能突出地刻画地下反射结构。所以,具备保留图像边界性质的总变差(TV)正则化是更为合适的选择。

TV正则化形式如下:

R(m)=‖m‖TV

(51)

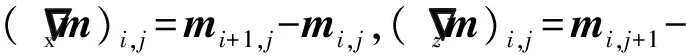
可利用如下迭代流程将TV正则化加入LSM迭代步骤中[14]。

初始化:u0=m0,k=0

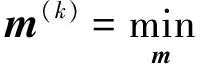
k=k+1

上述迭代流程中,对每一步迭代中的像进行TV去噪,并将去噪结果作为下一步迭代的先验信息,可以有效地去除像中的偏移假象和随机噪声,提高成像质量。

图5为实际数据常规LS-PSDM结果与TV正则化LS-PSDM结果对比,可以看出,TV正则化去除了成像结果中的随机噪声干扰,提高了同相轴的连续性,从而提高了成像质量。

图5 实际数据LS-PSDM结果对比a 常规LS-PSDM结果; b TV正则化LS-PSDM结果

5 针对反射系数的成像与针对散射强度的成像差异分析

到目前为止,本文讨论的内容都建立在地下介质分布是背景+散射的基础上。实质上,勘探地震所面对的介质可以描述为在空间上广泛分布的层状沉积层,加上火山活动、构造运动等引起的大、小尺度速度异常体(或波阻抗变化的异常体)。针对这样的介质情况,用背景+反射界面的方式来描述更为合适,体现了地下介质的特征和在其中传播的波场的特征。我们认为,基于地下介质特征和波场特征构建的成像方法和技术才是最实用的。

前已述及,针对散射的成像需要满足(28)式和(34)式规定的野外采集方式得到的数据。当前,仅仅在地表进行有限带宽和有限孔径的观测显然无法满足逆散射成像的要求。事实上,到目前为止，勘探地震成像技术都是基于反射波的,成像的目标是定位和估计反射界面的反射系数。勘探地震中,当前反射波成像理论可以总结为:在最小二乘成像理论框架下,假设地下介质是层状的(每层都终结于无穷远边界上)、观测系统是无穷宽方位和长偏移距及无假频采样的、背景速度正确(满足Born近似)且子波已知,则方位角度反射系数可以准确地估计出来并有一个半解析的表达形式[15]。COHEN等[16]和BLEISTEIN[17]等给出了上述成像方法完整的理论描述,这是勘探地震学家给出的反射波地震成像的最完整表达。

FWI(包括上述LS_RTM)都是针对散射体的成像,试图估计散射强度f(x)。仅有地表观测数据,根据当前FWI(LS_RTM)反演理论,很难给出反演解的精度评价。这是当前基于散射和逆散射成像理论的主要困境。

研究人员已经意识到了勘探地震的介质特点和波传播特点,提出了改进的LS_RTM方法:在LS_RTM的初始迭代中先进行反射系数的估计,即进行反射波最小二乘叠前深度偏移成像,然后再进行散射强度的估计。这一改进可以有效地改善LS_RTM的收敛效率,提高最终成像质量。

6 总结与讨论

油气地震勘探的目标是含油气储层的识别与描述。最核心的技术是地震波成像,得到地下介质的几何特征图像和弹性参数(主要是反射系数和波阻抗)。叠前深度偏移给出介质的几何特征图像,FWI(LS_RTM)试图给出弹性参数的估计。

基于散射波理论的FWI根本目标是给出宽(全)波数带的弹性参数估计。但是,它需要的数据是目前地表观测得到的有限带宽和有限孔径的无假频数据所无法满足的。依据这样不完整的数据得到的反演结果精度也很难评价。目前的FWI仅仅可以在低频长偏移距数据存在的情况下给出背景速度的估计;LS_RTM是在假设背景速度正确情况下的散(反)射波FWI。数据观测的不完整、叠前数据中的噪声、不准确的背景速度、正演(偏移)算子不能很好地模拟波现象、子波未知等因素导致LS_RTM很难收敛,解的精度难以评价。这是LS_RTM的困境,估计会一直伴随LS_RTM方法技术的发展过程,无法得到根本解决。

方位角度反射系数的估计是勘探地震学所独有的、针对勘探地震所面对的层状沉积地质特点以及波在层状介质中传播的特点而发展起来的成像方法,勘探地震学发展到现在主要是基于这样的反射波成像理论。

基于散射及逆散射成像的方法理论,到目前为止还没有得到实用性的有效证明。但是,首先进行基于反射系数的成像,在此基础上进行散射强度的成像无疑是可行的方法,可以有效地提高成像精度。针对散射波成像的正则化方法也有待进一步深入研究。

总之,尽管FWI方法具有看起来完美的反演理论,但基于散(反)射波振幅的高波数参数扰动量的估计目前缺乏有效的技术甚至缺乏明确的技术发展方向。这正是地震波成像方法理论研究需要着力的地方。

[1] WAPENAAR C P A.Inversion versus migration:a new perspective to an old discussion[J].Geophysics,1996,61(3):804-814

[2] CLAYTON R,STOLT R.A Born-WKBJ inversion method for acoustic reflection data[J].Geophysics,1981,46(11):1559-1567

[3] DEVANEY A J.Mathematical foundations of imaging,tomography and wavefield inversion[M].Cambridge:Cambridge University Press,2012:229-429

[4] SHUEY R.A simplification of the Zoeppritz equation[J].Geophysics,1985,50(4):609-614

[5] BLEISTEIN N.On the imaging of reflectors in the earth[J].Geophysics,1987,52(7):931-942

[6] BLEISTEIN N,COHEN J K,STOCKWELL J W.Mathematics of multidimensional seismic imaging,migration,and inversion[J].Applied Mechanics Reviews,2001,54(5):B94

[7] TARANTOLA A.Inversion of seismic reflection data in the acoustic approximation[J].Geophysics,1984,49(8):1259-1266

[8] STOLT R H,WEGLEIN A B.Migration and inversion of seismic data[J].Geophysics,1985,50(12):2458-2472

[9] STOLT R H,WEGLEIN A B.Seismic imaging and inversion[M].Cambridge:Cambridge University Press,2012:122-134

[10] WEGLEIN A B,VIOLETTE P B,KEHO T H.Using multiparameter Born theory to obtain certain exact multiparameter inversion goals[J].Geophysics,1986,51(5):1069-1074

[11] BORN M,WOLF E.Principles of optics[M].7th ed.Cambridge:Cambridge University Press,1999:695-732

[12] VAN LEEUWEN T,MULDER W A.A correlation-based misfit criterion for wave-equation traveltime tomography[J].Geophysical Journal International,2010,182(3):1383-1394

[13] 胡江涛.最小二乘逆时偏移及角度道集提取方法研究[D].上海:同济大学,2015 HU J T.Research on least-squares reverse time migration and angle gathers generation method[D].Shanghai:Tongji Universtiy,2015

[14] LIN Y,HUANG L.Least-squares reverse-time migration with modified total-variation regularization[J].Expanded Abstracts of 85thAnnual Internat SEG Mtg,2015:4264-4269

[15] LAMBARE G,OPERTO S,PODVIN P,et al.3D ray+Born migration/inversion,part I:theory[J].Geophysics,2003,68(4):1348-1356

[16] COHEN J K,HAGIN F,BLEISTEIN N.Three dimensional Born inversion with an arbitrary reference[J].Geophysics,1986,51(8):1552-1558

[17] BLEISTEIN N,COHEN J K,HAGIN F.Two and one-half dimensional Born inversion with an arbitrary reference[J].Geophysics,1987,52(1):26-36

(编辑：戴春秋)

Theory and method of least square prestack depth migration and imaging

WANG Huazhong1,HU Jiangtao1,2,GUO Song1

(1.Wavephenomenaandinversionimaginggroup(WPI),TongjiUniversity,Shanghai200092,China;2.StateKeyLaboratoryofOilandGasReservoirGeologyandExploitation,ChengduUniversityofTechnology,Chengdu610059,China)

The purpose of seismic imaging is firstly to determine the spatial location of the reflectivity or diffraction targets.After the structure of the reflection is settled,the rock parameters,related to velocity and density,can be estimated.Combined with the estimated elastic parameters and rock physics,the oil and gas reservoir can be delineated.We start from the seismic wave propagation representation of the scattered wave field and inverse scattering imaging.the formula of the scattered wave field is firstly given.The essence of the inverse scattering imaging is discussed,including the prestack seismic observed data and the corresponding observation mode required by inverse scattering imaging.Then,the theoretical framework of general linearized least-squares prestack depth migration (LS-PSDM) is given.The linearized LS-PSDM can be realized as long as the wave propagation operator calculated by Green functions can be reached.The least-squares reverse time migration (LS-RTM) is also discussed and the iterative realization method and the structure preserved total variation regularization method are given with numerical results.Finally,the differences between imaging methods based on reflectivity and scattering intensity estimation are analyzed.The most practical imaging methods aiming at the characteristics of medium and wave fields are stated.The inverse scattering imaging should be based on the methods.Further studies are required to testify whether the imaging methods based on scattered wave can satisfy the requirement of reservoir description.

scattered wave field representation,inverse scattering imaging,reflected wave imaging,least-squares prestack depth migration (LS_PSDM),full waveform inversion(FWI)

2016-10-09;改回日期：2016-12-06。

王华忠(1964—),男,教授,主要从事地震波传播、地震数据分析和地震波反演成像方面的研究工作。

胡江涛(1987—),男,博士,主要从事地震信号分析、地震波成像和反演方面的研究工作。

国家重点基础研究发展计划(973计划)(2011CB201002)、国家自然科学基金项目(41374117,41604100)和国家科技重大专项(2011ZX05005-005-008HZ,2011ZX05006-002,2011ZX05023)共同资助。

P631

A

1000-1441(2017)02-0159-12

10.3969/j.issn.1000-1441.2017.02.001

This research is financially supported by the National Key Basic Research and Development Program of China (973 Program) (Grant No.2011CB201002),the National Natural Science Foundation of China (Grant Nos.41374117,41604100),the National Science and Technology Major Project (Grant Nos.2011ZX05005-005-008HZ,2011ZX05006-002,2011ZX05023).

王华忠,胡江涛,郭颂.最小二乘叠前深度偏移成像理论与方法[J].石油物探,2017,56(2):-170

WANG Huazhong,HU Jiangtao,GUO Song.Theory and method of least square prestack depth migration and imaging[J].Geophysical Prospecting for Petroleum,2017,56(2):-170