基于孔隙分类理论的自相容模型横波速度预测方法

熊晓军,李 翔,刘 阳,简世凯

(油气藏地质及开发工程国家重点实验室,四川成都610059)



基于孔隙分类理论的自相容模型横波速度预测方法

熊晓军,李 翔,刘 阳,简世凯

(油气藏地质及开发工程国家重点实验室,四川成都610059)

岩石物理建模是求取横波速度的重要手段之一,针对勘探开发过程中缺少横波速度资料的情况,研发了一种基于等效自相容近似(SCA)模型的碎屑岩地区横波速度计算方法。首先基于孔隙分类理论计算碎屑岩中含束缚水的无效孔隙大小;然后将无效孔隙作为岩石基质成分进行建模;再利用有效孔隙建立岩石骨架并进行流体饱和计算;最后在实测纵波速度约束下,通过调整岩石基质各组分大小迭代计算横波速度。试验结果证明,该方法预测四川盆地碎屑岩地区横波速度的精度较高,有一定的推广意义。

孔隙分类;等效自相容近似模型;横波速度预测;岩石物理建模;平均相对误差

横波速度是叠前反演及属性提取中的必要信息,在缺少横波数据时,可以利用一些经验公式估算横波速度,通常可以利用孔隙度信息预测横波速度。一些学者给出部分常用的经验公式:HAN等[1]通过超声试验发现纯砂岩纵、横波速度与孔隙度之间的经验关系准确性较高,并在不同压力条件下拟合出相应的经验公式;基于HAN的思路,EBERHART-PHILLIPS[2]进一步拟合出了饱和水砂岩的纵横波速度与孔隙度之间的经验关系;CASTAGNA等[3]探索了纵、横波速度之间的经验关系以及与孔隙度和泥质含量的关系等。

利用经验关系估算横波速度可行但准确度不高[4],尤其当地层岩性、物性变化较大时,通常基于岩石物理模型进行横波速度预测[5-19]。岩石物理建模方法是根据岩石物性对其进行等效建模计算的方法,通过计算得到岩石的等效弹性参数从而进一步计算岩石的纵横波速度。在岩石物理建模过程中,需要充分考虑岩石所含的基质矿物种类、岩石孔隙度、孔隙形状及岩石的含流体性等因素[15]。XU等[16]将碎屑岩孔隙空间分为具有较小孔隙扁率的泥岩孔隙和具有较大孔隙扁率的砂岩孔隙,并对碎屑岩进行简化建模;张广智等[17]改进了Xu-White模型并用于碳酸盐岩储层的横波速度预测,并将相应的孔隙类型分为粒间孔隙、溶洞及裂缝;熊晓军等[18-19]基于Xu-White模型采用基质矿物等效弹性模量进行反演,提高了横波速度预测的精度。以上方法核心思想均基于Xu-White模型,其孔隙分类方法主要是将碎屑岩中的孔隙分为泥岩孔隙和砂岩孔隙,并根据相应孔隙的扁率差异进行建模计算。

随着研究深入,常规的Xu-White模型孔隙分类方法已经不能很好地满足建模精度,其本质原因是碎屑岩中泥质成分包含束缚水的孔隙,并不能储集其它流体,其对于油气勘探相当于无效孔隙,不应作为储集空间进行建模。一些学者基于该观点开展了一些研究工作,印兴耀教授基于有效孔隙分类方法进行了横波速度预测,采用了微分等效介质模型(DEM)进行岩石物理建模计算横波速度[15]。由于DEM建模过程中需充分考虑各组分的添加顺序,最终计算得到的等效模量依赖于建模过程中主相和包含物的添加顺序。也就是说,材料一作为主相向其中添加包含物材料二所得的计算结果,不同于材料二作为主相向其中添加包含物材料一的计算结果。碎屑岩地层可能含大量泥质成分,计算时不能认定主相恒定为石英、长石等矿物组合,也不能给定包含物为粘土矿物。因此需要给出一种计算结果不受限于各矿物组分添加顺序的计算方法。本文基于孔隙分类理论,将泥质中的含束缚水孔隙判断为无效孔隙并作为岩石基质组成成分,对有效孔隙进行流体替换,其物理意义更加鲜明,并基于等效自相容近似(SCA)模型进行建模计算,建模过程无需考虑各矿物组分添加顺序,该方法对碎屑岩地区横波速度预测较准确。

1 方法原理

1.1 孔隙分类方法

1.1.1 常规Xu-White模型孔隙分类方法

Xu-White将碎屑岩孔隙空间分为具有较小孔隙扁率的泥岩孔隙和具有较大孔隙扁率的砂岩孔隙。若将φtotal定义为岩石孔隙度,则:

(1)

式中:φclay为较柔软的泥岩孔隙度;φsand为刚性较大的砂岩孔隙度。泥岩岩石骨架体积分数υc和砂岩岩石骨架体积分数υs可以用来估计φclay和φsand,当υc+υs=1时,假设φclay和φsand与υc和υs各自成比例,则:

(2)

(3)

1.1.2 基于有效性的孔隙分类方法

DVORKIN等[20]发现岩石中所含束缚水的泥岩孔隙对岩石速度影响较为明显,基于Xu-White模型的孔隙分类方法,进一步将岩石孔隙分为有效孔隙和无效孔隙。

φtotal=φsand+φclay=[φsand+(1-q)φclay]+qφclay

=φeff+φueff

(4)

式中:φtotal表示总孔隙度大小(孔隙度测井结果);φeff表示有效孔隙度;φueff表示无效孔隙度;比例系数q表示泥岩孔隙中的无效部分和有效部分的比值。通常认为泥岩中连通的孔隙为有效孔隙,含束缚水的孔隙为无效孔隙。

1.2 岩石物理建模方法

本文针对碎屑岩储层进行横波反演,首先采用Voight-Reuss-Hill平均模型计算岩石背景等效模量[4],公式如下:

(5)

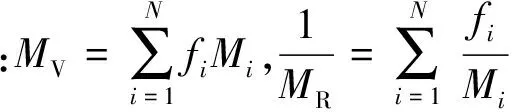
计算得到岩石背景等效弹性模量后,基于等效自相容近似(SCA)模型向岩石基质背景中加入粘土及泥质中含束缚水的无效孔隙。采用BERRYMAN[21]提出的N相成分混合的等效自相容近似模型进行计算,形式如下:

(6)

(7)

在上述过程中,泥质中所含束缚水的无效孔隙度可以用总孔隙度减去有效孔隙度得到,而有效孔隙度可基于密度测井求取,含流体纯岩石孔隙度公式如下:

(8)

式中:ρmatrix表示岩石骨架密度;ρsat表示饱和流体岩石密度;ρfluid表示孔隙流体密度。现代测井解释中,无论地层是何种岩性,当给定ρmatrix=2.71g/cm3时,计算结果为纯岩石的视石灰岩孔隙度。(8)式中的岩石骨架密度ρmatrix通过Voight-Reuss-Hill平均模型建模计算得到,建模过程中不添加粘土,即不引入泥质所含的束缚水孔隙,所求得的孔隙度大小认为是碎屑岩不含束缚水的有效孔隙度。

在此基础上,应用简化的Xu-White模型(Key-Xu)进行有效孔隙添加,计算公式如下:

(9)

(10)

式中:K(φ)和μ(φ)为由简化的Xu-White模型计算的与有效孔隙度φ有关的体积模量与剪切模量;K0和μ0为岩石等效基质弹性模量。系数p和q定义为:

(11)

(12)

式中:Tiijj(αl)和Fiijj(αl)为Eshellby张量;l为当前矿物成分;αl为不同类型孔隙扁率;υl为岩石组分体积分量。应用简化的Xu-White模型求解干岩石骨架模量参数,可以简化基于微分等效介质理论的Kuster-Toksöz方程的非线性常微分方程求解问题。当逐渐增加岩石有效孔隙度并变化孔隙扁率时,利用简化的Xu-White模型可以有效解决耦合方程组求解问题。

至此得到含空孔隙的干岩石骨架等效弹性模量,在此基础上基于Gassmann方程进行流体替换得到饱和流体岩石等效体积模量,计算公式如下:

(13)

式中:Kdry为简化Xu-White模型计算结果;φ为计算得到的有效孔隙度大小;Kfl为相应流体的体积模量;Ksat为最终计算得到的饱和流体岩石等效体积模量。

上述计算过程中所使用的各种矿物及流体的岩石物理参数如表1所示。

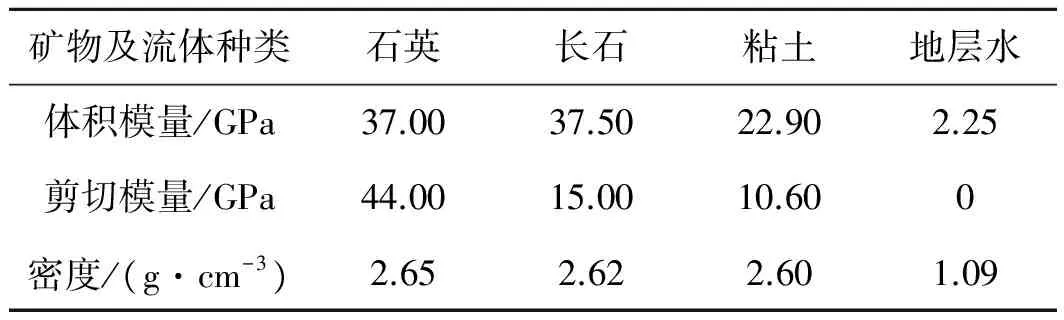
表1 建模过程中的岩石物理参数

在建模计算过程中将孔隙分为两类:一类是具有较大孔隙扁率的砂岩孔隙;另一类是具有较小孔隙扁率的泥岩孔隙。等效自相容建模过程中,将所添加的无效孔隙扁率设为泥岩扁率(文中给值0.035);应用简化Xu-White模型添加有效孔隙时,孔隙形状为砂岩孔隙,由于需要变化孔隙扁率计算,故将其迭代变化的上限设为0.8。

充分利用上述各种岩石物理模型及参数进行建模,其建模过程可分为如下几步:

1) 分析碎屑岩工区背景矿物成分,基于Voight-Reuss-Hill平均模型计算岩石背景体积模量;

2) 基于SCA模型将粘土和无效孔隙添加进岩石背景组分中,从而得到含无效孔隙的岩石基质弹性模量;

3) 利用改进的Xu-White模型,向岩石基质中添加有效孔隙组分,计算得到干岩石弹性模量;

4) 基于测井资料中流体饱和度信息,通过Gassmann方程在含流体井段对干岩石进行流体添加,得到最终饱和流体岩石弹性模量。

上述岩石物理建模流程见图1。

图1 基于孔隙分类的岩石物理建模流程

1.3 横波反演方法

依据测井数据和1.2节所述步骤建立岩石物理模型,分别计算岩石背景弹性模量、岩石基质弹性模量、干岩石骨架弹性模量和饱和流体岩石弹性模量。用求得的饱和流体体积模量Ksat和剪切模量μsat结合密度测井资料计算纵、横波速度,公式如下:

(14)

算法受实测纵波速度约束,在基质弹性模量SCA模型建模过程中,通过不断调整岩石背景组分含量和粘土(泥质)组分含量计算得到岩石基质弹性模量,并据此计算饱和岩石体积模量,根据(14)式计算纵、横波速度。当反演计算的纵波速度与实测纵波速度差值满足精度要求时,输出此时的纵、横波速度作为反演速度。

2 实际计算应用

本文提出的横波速度反演算法在迭代过程中需不断调整岩石背景组分和粘土(泥质)组分,将反演纵波速度与实测纵波速度差值很小作为该反演算法的收敛条件。图2a为工区L3井测井解释的泥质含量曲线;图2b为本文反演算法满足收敛条件下输出的反演泥质含量曲线。对比图2a和图2b发现,本文方法所反演的泥质含量与真实测井解释泥质含量趋势十分相似,值域分布一致,4980m以下泥质含量明显增大,反演结果与测井解释结果相似。

经统计,真实测井解释的平均泥质含量为26.0%,反演得到的平均泥质含量为24.6%,充分说明本文通过矿物组分迭代的横波速度预测方法对碎屑岩地区较为有效。与此同时,相较于常规Xu-White模型横波速度预测方法需要输入泥质含量作为计算参数,本文方法可以不用输入泥质含量,适用性更强。

图2 L3井泥质含量曲线a 测井解释泥质含量曲线; b 本文算法反演泥质含量曲线

将本文反演方法应用于四川盆地碎屑岩地区的横波速度预测,研究区内L3井和L4井具有真实横波测井资料。将预测结果与真实横波测井结果进行对比并统计反演结果的相对误差,如图3和图4所示。图3a 和图4a分别是L3井和L4井的真实测井纵波速度和基于本文方法得到的纵波速度曲线对比图,由于横波反演算法基于实测纵波数据约束,所以反演的纵波与实测纵波速度曲线几乎完全重合。图3b 和图3c分别为L3井采用本文方法和常规Xu-White模型反演方法得到的横波速度与真实横波速度对比图;图4b和图4c分别为L4井采用本文方法和常规Xu-White模型反演方法得到的横波速度与真实横波速度对比图。其中,黑线代表实测横波速度,红线代表反演横波速度。由图3b,图3c,图4b和图4c可见,本文预测横波速度与真实横波速度趋势完全一致,差异较小;常规Xu-White模型预测横波速度曲线跳动较大,效果一般。

图3 L3井预测结果与真实横波测井结果对比a 预测纵波速度与真实纵波速度; b 本文方法预测横波速度与真实横波速度; c 常规Xu-White模型预测横波速度与真实横波速度; d 本文方法与常规Xu-White方法预测结果与真实速度的相对误差曲线

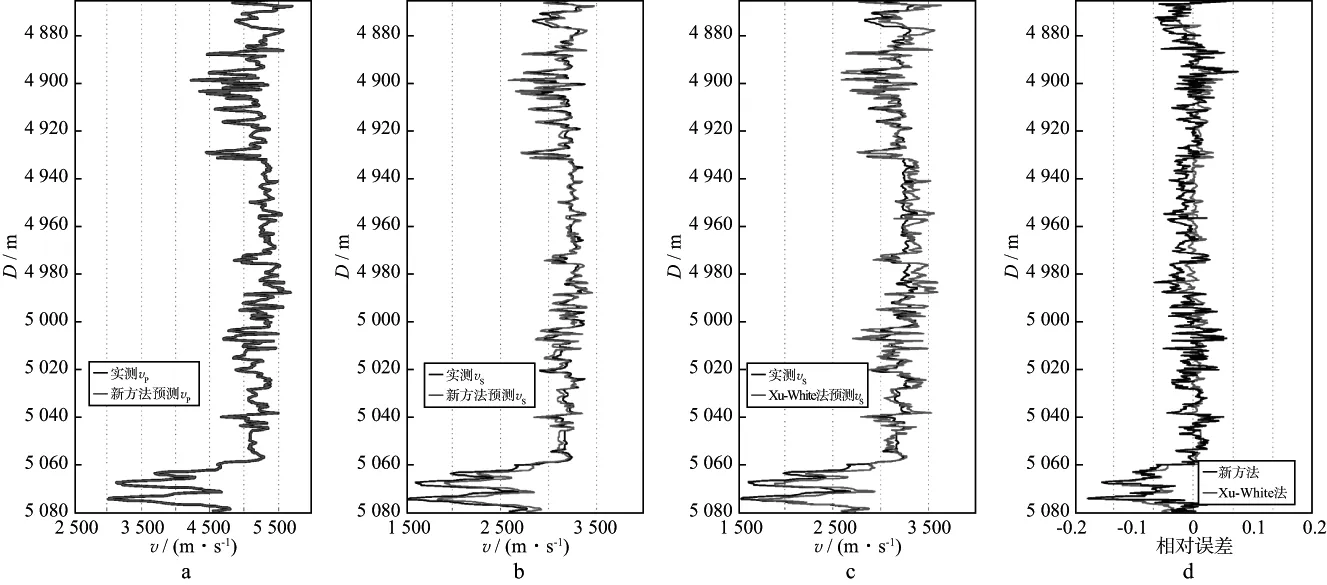
图4 L4井预测结果与真实横波测井结果对比a 预测纵波速度与真实纵波速度; b 本文方法预测横波速度与真实横波速度; c 常规Xu-White模型预测横波速度与真实横波速度; d 本文方法与常规Xu-White方法预测结果与真实速度的相对误差曲线

图3d和图4d分别为L3井和L4井采用两种横波速度预测方法计算得到的相对误差曲线。经统计,本文方法在L3井预测的平均相对误差为1.6%,常规Xu-White模型横波速度预测平均误差为2.8%;本文方法应用到L4井的平均相对误差为2.4%,常规Xu-White模型横波速度预测平均误差为3.3%。实例证明了本文方法在碎屑岩地区对横波速度预测的精度较高,具有一定的有效性。

3 结论

本文基于岩石物理建模方法建立了一种碎屑岩地区横波速度预测方法,并将此方法应用于四川盆地两口含横波资料井的横波速度预测,得到如下结论:

1) 基于孔隙分类的观点能进一步区分泥质中的连通孔隙和含束缚水孔隙,在岩石物理建模过程中,将无效的含束缚水孔隙当做干岩石骨架组分,将有效孔隙作为能够储存流体的孔隙空间,并进行流体替换,其物理意义更加鲜明,建模方法更加准确。

2) 与基于微分等效模型(DEM)的建模方法不同,基于等效自相容近似(SCA)模型的建模方法无需考虑各组分及包含物的添加顺序,在高粘土含量的碎屑岩中无需考虑矿物添加顺序。等效自相容近似(SCA)模型中变量耦合,通过迭代计算至收敛时输出结果,准确性更高。

3) 反演横波速度时,不断调整背景及泥质组分大小,将反演纵波速度与真实纵波速度差值达到预测精度作为收敛条件，此时输出反演结果。实际应用证明反演得到的泥质含量与测井解释的泥质含量基本一致。整个反演过程无需输入泥质含量作为计算参数,适用于碎屑岩地区横波速度预测。

4) 本文所述的方法应用于四川盆地碎屑岩地区横波速度预测,预测结果与实际测井结果差异小,预测效果较常规Xu-White模型计算结果更为准确,平均相对误差在2%左右,满足生产中的横波速度预测精度要求,具有一定的推广意义。

[1] HAN D H,NUR A,MORGAN D.Effects of porosity and clay content on wave velocities in sandstones[J].Geophysics,1986,51(11):2093-2107

[2] EBERHART-PHILLIPS D M.Investigation of crustal structure and active tectonic processes in the coast ranges[D].USA:Stanford University,1989

[3] CASTAGNA J P,BATZLE M L,EASTWOOD R L.Relationships between compressional wave and shear-wave velocities in clastic silicate rocks[J].Geophysics,1985,50(4):571-581

[4] MAVKO G,MUKERJI T,DVORKIN J.The rock physics handbook,second edition:tools for seismic analysis of porous media[M].New York：Cambridge University Press,2009:1-511

[5] 郭栋,印兴耀,吴国忱.横波速度计算方法与应用[J].石油地球物理勘探,2007,42(5):535-538 GUO D,YIN X Y,WU G C.Computational approach of S-wave velocity and application[J].Oil Geophysical Prospecting,2007,42(5):535-538

[6] 谢月芳,张纪.岩石物理模型在横波速度估算中的应用[J].石油物探,2012,51(1)：65-70 XIE Y F,ZHANG J.Application of rock physical model in S-wave velocity estimation[J].Geophysical Prospecting for Petroleum,2012,51(1)：65-70

[7] 张元中,周开金,赵建斌,等.砂泥岩地层横波测井曲线预测方法研究[J].石油物探,2012,51(5):508-514 ZHANG Y Z,ZHOU K J,ZHAO J B,et al.Shear-wave logging curve prediction method for shaly sand formation[J].Geophysical Prospecting for Petroleum,2012,51(5):508-514

[8] 胡起,陈小宏,李景叶.基于各向异性岩石物理模型的页岩气储层横波速度预测[J].石油物探,2014,53(3):254-261 HU Q,CHEN X H,LI J Y.Shear wave velocity prediction for shale gas resevoirs based on anisotropic rock physics model[J].Geophysical Prospecting for Petroleum,2014,53(3):254-261

[9] 武文来,印兴耀.岩石物理参数与地球物理特征关系研究——以QHD326油田为例[J].石油物探,2008,47(3):235-243 WU W L,YIN X Y.Study of relationship between petrophysical parameters and geophysical characteristics:case study of QHD326 oilfield[J].Geophysical Prospecting for Petroleum,2008,47(3):235-243

[10] 白俊雨,宋志翔,苏凌,等.基于Xu-White模型横波速度预测的误差分析[J].地球物理学报,2012,55(2):589-595 BAI J Y,SONG Z X,SU L,et al.Error analysis of shear-velocity prediction by the Xu-White model[J].Chinese Journal of Geophysics,2012,55(2):589-595

[11] 云美厚,管志宁.储层条件下砂岩纵波和横波速度的理论计算[J].石油物探,2002,41(3):289-292 YUN M H,GUAN Z N.The estimation of P and S-wave velocities in sandstone under in-situ conditions[J].Geophysical Prospecting for Petroleum,2002,41(3):289-292

[12] 熊晓军,吕龑,林凯,等.一种碳酸盐岩流体替换新方法[J].中国石油大学学报:自然科学版,2012,36(6):57-61 XIONG X J,LV Y,LIN K,et al.A novel method of fluid substitution in carbonates[J].Journal of China University of Petroleum,2012,36(6):57-61

[13] 孙福利,杨长春,麻三怀,等.横波速度预测方法[J].地球物理学进展,2008,23(2):470-474 SUN F L,YANG C C,MA S H,et al.An S-wave velocity predicted method[J].Progress in Geophysics,2008,23(2):470-474

[14] 董宁,霍志周,孙赞东,等.泥页岩岩石物理建模研究[J].地球物理学报,2014,57(6):1990-1998 DONG N,HUO Z Z,SUN Z D,et al.An investigation of a new rock physics model for shale[J].Chinese Jounal of Geophysics,2014,57(6):1990-1998

[15] 印兴耀,李龙．基于岩石物理模型的纵、横波速度反演方法[J].石油物探,2015,54(3):249-253 YIN X Y,LI L.P-wave and S-wave velocities inversion based on rock physics model[J].Geophysical Prospecting for Petroleum,2015,54(3):249-253

[16] XU S,WHITE R E.A physical model for shear-wave velocity prediction[J].Geophysical Prospecting,1996,44(4):687-717

[17] 张广智,李呈呈,印兴耀,等．基于修正Xu-White模型的碳酸盐岩横波速度估算方法[J].石油地球物理勘探,2012,47(5):717-722 ZHANG G Z,LI C C,YIN X Y,et al.A shear velocity estimation method for carbonate rocks based on the improved Xu-White model[J].Oil Geophysical Prospecting,2012,47(5):717-722

[18] 熊晓军,林凯,贺振华．基于等效弹性模量反演的横波速度预测方法[J].石油地球物理勘探,2012,47(5):723-727 XIONG X J,LIN K,HE Z H.A method for S-wave velocity estimation based on equivalent elastic modulus inversion[J].Oil Geophysical Prospecting,2012,47(5):723-727

[19] 林凯,贺振华,熊晓军,等．基于基质矿物模量自适应提取横波速度反演方法[J].石油地球物理勘探,2013,48(2):262-267 LIN K,HE Z H,XIONG X J,et al.S-wave velocity inversion based on adaptive extraction of matrix mineral modulus[J].Oil Geophysical Prospecting,2013,48(2):262-267

[20] DVORKIN J,MAVKO G,GUREVICH B.Fluid substitution in shaley sediment using effective porosity[J].Geophysics,2007,72(3):1-8

[21] BERRYMAN J G.Mixture theories for rock properties[C]//Rock physics and phase relations:a handbook of physical constants.Washington,DC:American Geophysical Union,1995:205-228

(编辑：陈 杰)

Shear wave velocity estimation method by the porosity classificationbased on the self-consistent model

XIONG Xiaojun,LI Xiang,LIU Yang,JIAN Shikai

(StateKeyLabofOilandGasReservoirGeologyandExploitation,ChengduUniversityofTechnology,Chengdu610059,China)

The rock physics modeling is an important means for obtaining the shear wave velocity data in exploration and development.We have developed a shear wave velocity estimation method based on the self-consistent approximations (SCA) model.Firstly,based on the theory of porosity classification we calculate the inactive porosity with bound water in clastic rocks and get it as the rock matrix components.Then we make use of effective porosity as the rock frame and conduct the fluid saturated calculation.Finally,we take the measured P-wave velocity as the constraint and calculate the shear wave velocity by adjusting the size of the components in the rock matrix iteratively.The method has higher precision for shear wave velocity estimation in clastic rocks in Sichuan Basin and is worth to promote.

porosity classification,self-consistent approximations (SCA) model,shear-wave velocity estimation,rock physics modeling,the average relative error

2016-04-18;改回日期：2016-05-31。

熊晓军(1980—),男,博士,教授,现主要从事岩石物理分析及油气地震勘探新方法研究。

国家自然科学基金项目(41274130)资助。

P631

A

1000-1441(2017)02-0179-06

10.3969/j.issn.1000-1441.2017.02.003

This research is financially supported by the National Natural Science Foundation of China (Grant No.41274130).

熊晓军,李翔,刘阳,等.基于孔隙分类理论的自相容模型横波速度预测方法[J].石油物探,2017,56(2):-184

XIONG Xiaojun,LI Xiang,LIU Yang,et al.Shear wave velocity estimation method by the porosity classification based on the self-consistent model[J].Geophysical Prospecting for Petroleum,2017,56(2):-184