用于自复位结构的新型钢板剪力墙的抗震性能分析

李 乾，李启才

（苏州科技大学 江苏省结构工程重点实验室，江苏 苏州 215011）

用于自复位结构的新型钢板剪力墙的抗震性能分析

李 乾，李启才

（苏州科技大学 江苏省结构工程重点实验室，江苏 苏州 215011）

为了研究薄钢板在自复位钢结构中的耗能以及复位能力，提出了一种新型钢板剪力墙。对其构造和工作原理进行了详细说明。通过有限元软件ANSYS对不同厚度的5个试件模型进行模拟，得出滞回曲线、骨架曲线、耗能曲线、承载力退化曲线及刚度退化曲线。随后，围绕着结构的强度、刚度、延性和复位性能，展开参数分析。分析结果表明：两侧加劲方管能有效约束试件的面外变形，使结构具有良好的复位效果；随着钢板厚度t的增加，整体结构的耗能能力和承载能力也会增强，但是复位性能会变差。

自复位钢框架；新型钢板剪力墙；滞回曲线；环线刚度；累积耗能；能量耗散系数

传统的钢结构体系通过自身材料特性和结构变形来抵抗地震动，耗散地震能量，可能震后没有倒塌但却往往有很大的残余变形，或者在结构的某些薄弱部位发生脆性破坏[1]。这些变形及破坏，增加了震后结构加固及修复的难度。而自复位结构与传统框架结构相比，在地震作用下残余变形会小得多。其核心理念在于能使框架结构在地震力作用下主体结构始终处于弹性状态，并通过预应力钢绞线等元件的设置为主体结构提供足够的恢复力，使主体结构在震后及时恢复，而结构的耗能能力和塑性变形集中在易拆换的耗能构件上。

2001年，J．Ricles等[2]率先实现了钢框架结构的自复位性能，如图1所示。通过在梁高度范围内布置预应力钢绞线来提供自复位能力，利用梁上下翼缘处的连接角钢传递竖向剪力和进行地震荷载作用下的能量耗散。2005年，M.Maria等[3]研究了初始预应力大小、预应力束的数量以及加强板的长度对自复位节点转动变形性能的影响。

由于连接角钢耗能有限，Dowden[4]用抗侧及耗能能力更突出的无加劲薄钢板剪力墙作为自复位框架的耗能构件，提出了自复位钢板剪力墙结构体系（SC-SPSWs）。根据Ma Xiang[5]对蝴蝶形短柱的理论研究，将其改进并应用到自复位钢板剪力墙结构中，从而形成新型的自复位钢板剪力墙结构，如图2所示。

利用有限元软件ANSYS对结构进行三维模拟分析，探索钢板厚度对结构的耗能能力、承载力、刚度、延性和复位能力的影响。

图1 具有自复位功能的钢节点

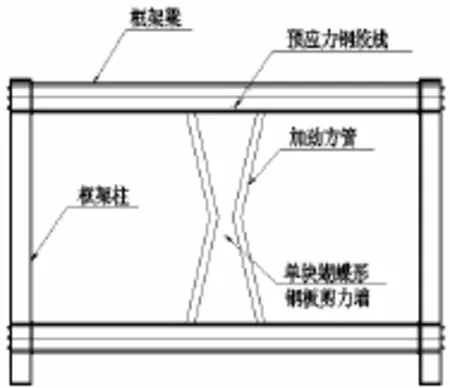
图 2 新型钢板剪力墙-自复位钢框架结构

1 有限元分析方法及验证

对试件编号为JD4的自复位节点进行模拟验证[6]。框架梁柱均采用Q345B做成的 H形钢，梁柱连接处用角钢相连，梁柱钢绞线的应力-应变本构关系均采用试验实测值。对于Q345钢：σy=440 MPa，σu=575 MPa，E=200 000 MPa，强化模量取为0.02E，泊松比v=0.3；钢绞线σy=1 586 MPa，弹性模量E=195 000 MPa，强化模量为0.01E。梁截面尺寸为500×300×28×14，梁的长度取3.8 m，框架柱的截面尺寸为500×500×20×20，柱的长度取上下层反弯点之间距离为3 m。自复位梁柱节点通过角钢和钢绞线连接，角钢尺寸L200×14，长度取300 mm，在梁的上下翼缘处均应布置，钢绞线采用15-7Φ5，抗拉强度为1 860 MPa，共有4根，沿梁腹板两侧各对称分布两根，并沿着梁长方向穿过柱的内翼缘在外翼缘处锚固，初始预拉力为60 kN。

梁柱采用SHELL181单元，钢绞线采用LINK10单元，采用映射划分单元，打开大变形和线性搜索开关，采用稀疏矩阵求解器进行计算。加载方式与试验相同，先加载预应力再加载水平位移到层间位移角为5%为止。

其中有限元模型及加载耦合方式见图3（a）所示，图3（b）、3（c）所示为试验和模拟所得的滞回曲线。从模拟曲线图中可以看出典型的“双旗帜状”，滞回环较饱满，而且荷载卸载到零时结构位移也变为零，说明模拟的复位能力满足要求。而且模拟时得到极限承载力为82.5 kN，较试验84.7 kN的承载力减小2.6﹪，在误差容许范围内，说明承载力也满足要求。但模拟中采用的耦合加载方式以及对梁柱连接区域角钢的简化，导致结构的初始刚度和耗能能力较试验的有所下降，但均满足模拟验证精度要求。

图 3 自复位节点验证

2 有限元分析试件模型参数

图4为BASE试件的有限元模型图。通过改变钢板厚度，设计出XG系列模型试件。此模型结构的跨度为5 350 mm，层高为3 780 mm。框架梁柱截面尺寸分别为HN350×220×12×16和HW250×250×12×16，梁柱钢材均采用Q345B。钢板剪力墙宽度、高度的取值分别为980、2 630 mm，钢材采用Q235B。

为了防止钢板剪力墙结构在竖向荷载作用下发生提前屈曲，采用在墙板上增加竖向加劲矩形钢管的方法。钢管截面为□140 mm×100 mm×3 mm。梁柱之间通过沿梁长分布的6根钢绞线连接，每根钢绞线的截面面积为540 mm2，初始预拉力为175 kN[7]。

建模时，结构中选用的钢材和钢绞线，均采用双折线弹塑性材料模型，取名义屈服强度。钢绞线的弹性模量E=1.95×105MPa，强化模量为0.01E；钢材的弹性模量E=2.0×105MPa，强化模量为0.02E。

梁柱和钢板截面均采用shell181单元；钢绞线选取受拉Link10单元，用PRETS179单元定义预张紧区域，施加初始预应力；梁柱节点间设置接触对，接触面积为350×220，采用TARGE 170目标单元和CONTA 174接触单元模拟结构摆动过程中梁柱的脱开和闭合，把梁柱接触部分的柱内翼缘作为目标单元，与之相对应的梁端板作为接触单元。

为了模拟柱脚铰接，选取左右两柱底板中心线上Z方向所有节点，约束其UX、UY、UZ三个方向的自由度，再选取两柱柱顶盖板X方向中心线上所有节点，约束其UZ方向自由度，防止框架柱发生过大的扭转变形。选取框架梁腹板中线X方向的节点，约束其Z方向的平动自由度以及ROTZ方向的转动自由度，这样可以约束框架梁的扭转变形及面外变形。为了避免加载点的应力集中，选取框架右柱顶端盖板的所有节点，对其进行X方向的耦合，把耦合的主节点作为模型的加载点。加载制度如图5所示，每个循环加载3圈。分析过程打开大变形选项和非线性搜索选项。XG系列模型试件具体参数如表1所示。

图4 BASE试件有限元模型

图5 加载制度

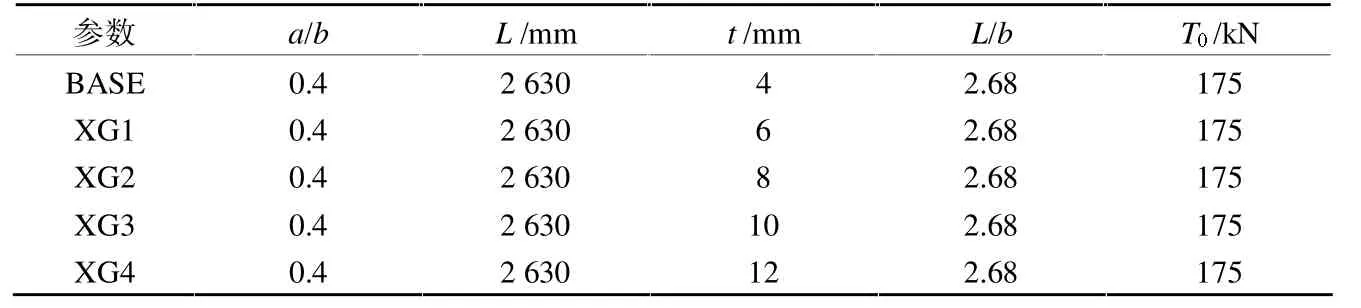
表1 XG系列试件参数

3 模型性能参数分析

3.1 滞回曲线及骨架曲线

XG系列模型试件在循环往复荷载作用下所得到的滞回曲线如图6所示。观察图形可以发现，采用较薄钢板剪力墙的试件，滞回曲线呈现出自复位耗能结构典型的“双旗帜”特点，这是由于预应力钢绞线为结构提供一定的恢复力，使结构出现了明显的复位现象。同时值得注意的是，在层间位移增大的过程中，曲线没有出现荷载下降段，说明了该类型结构良好的延性性能。

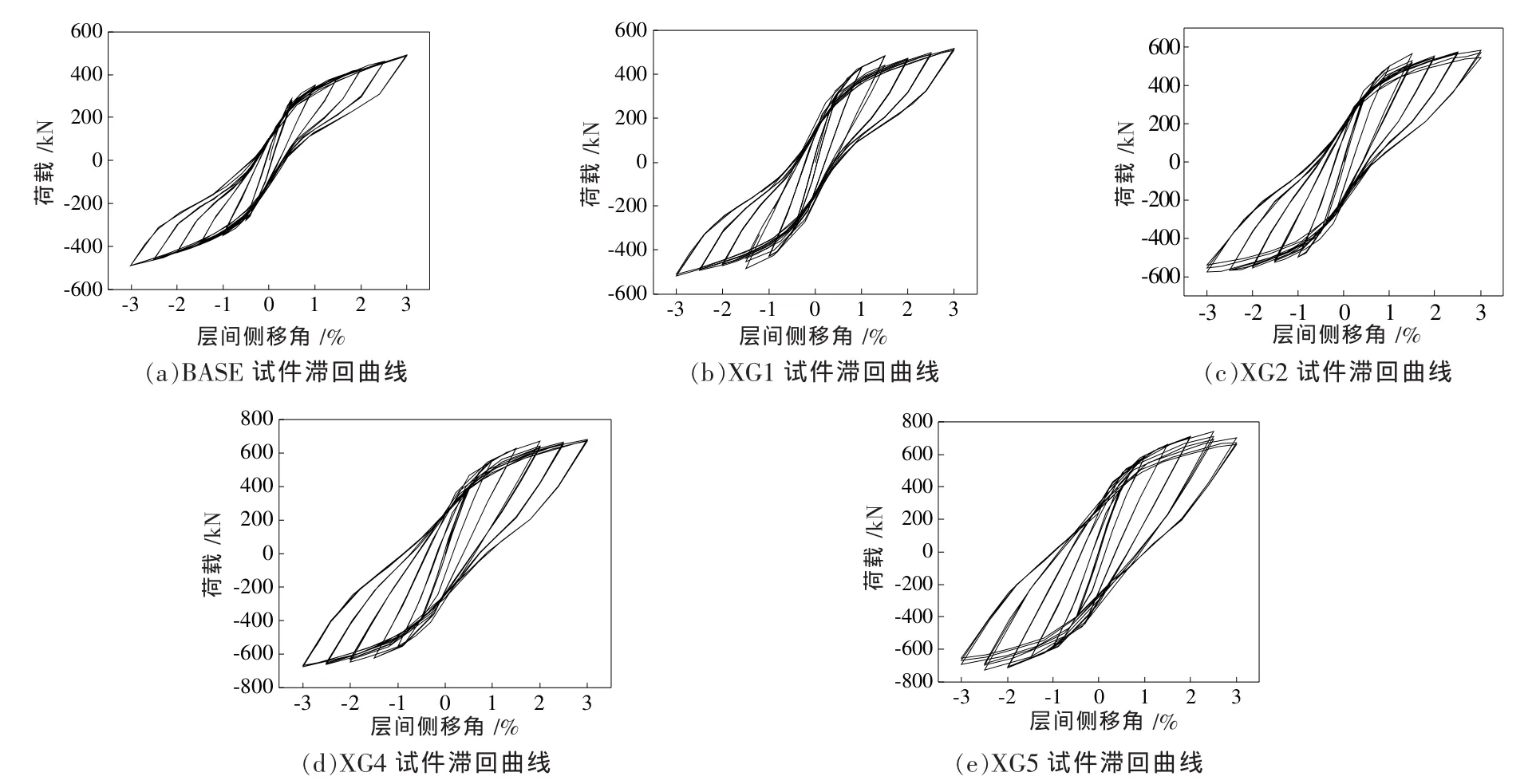
图6 XG系列试件滞回曲线

3.2 复位能力

自复位结构复位能力的衡量指标是残余层间位移角，即完全撤去外力时，结构相比初始状态所偏移的位移。其本质主要是结构耗能部件进入塑性耗能。我国抗震规范[8]规定：多高层钢结构弹塑性层间位移角限值为1/50，因此取层间侧移角为2%所对应的残余层间侧移角进行复位能力的比较。

XG系列试件中BASE、XG1、XG2、XG3、XG4模型试件在2%层间侧移时所对应的残余层间位移角 分别为[-0.28%，0.28%]、[-0.36%，0.39%]、[-0.48%，0.49%]、[-0.53%，0.56%]、[-0.65%，0.68%]。从图6试件的滞回曲线中可以看出，随着厚度的增加，结构的承载能力以及耗能能力虽然得到增强，但结构的复位能力却降低。Baldvins[9]提出将残余层间位移角限值控制在0.5%以内，仅需要替换耗能器就能快速恢复结构的使用功能。可见BASE试件和XG1、XG2试件满足自复位结构震后快速复位要求，而XG3、XG4试件需震后修复后才能投入使用。

3.3 耗能能力

钢板剪力墙-自复位钢框架结构的耗能主要集中于相对较薄的钢板，利用钢板进入塑性耗能。钢板耗能越多，则钢框架主体结构所耗散的能量就将变少，从而达到有效保护自复位钢框架主体结构不破坏的目的。

通常用荷载-位移滞回曲线所包围的面积来衡量试件的耗能能力，滞回曲线所围成的面积越大，试件的耗能能力越出色。图7为试件的耗能E0循环次数n曲线，图8为试件的累积耗能ΣE0循环次数n曲线。

在反复荷载作用下，滞回环面积受到强度和刚度退化的影响。为了表达这一特性，引入能量耗散系数E，如图9所示。能量耗散系数E即每个往复加载周期内滞回环所围成的面积S（BCD+DAB）与卸载端至横坐标之间形成的三角形面积S（OCF+OAE）的比值[10]，即

根据图8以及公式（1）计算得出的XG系列试件所对应的能量耗散系数如图9所示。由图9可知，加载初期，模型试件处于弹性阶段，能量耗散系数较小；随着位移增大，耗能钢板进入弹塑性工作阶段，耗能能力提升，能量耗散系数也随之增大。BASE、XG1、XG2试件在层间位移角为2%附近达到极值，XG3、XG4试件在层间位移角为2.5%附近达到极值；再增大位移时，由于耗能钢板的面外变形增大，影响到钢板耗能能力的发挥，因此能量耗散系数会出现一个下降的趋势。总的来看，随着厚度的增加，能量耗散系数越大，耗能能力越突出，复位能力越差。

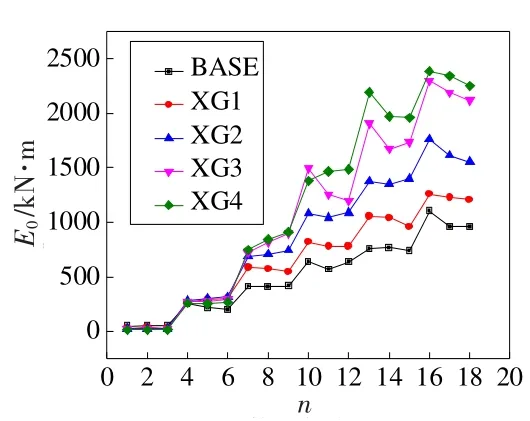
图7 XG系列试件耗能

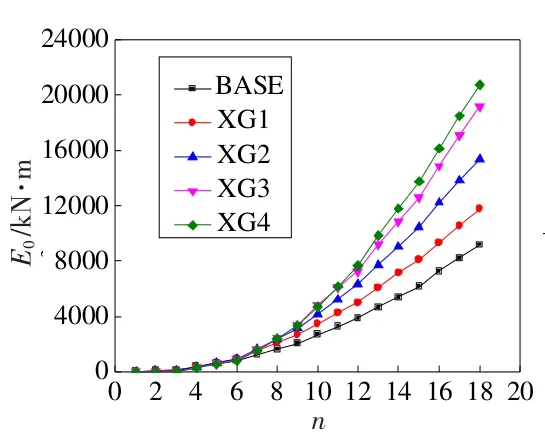
图8 XG系列试件累积耗能

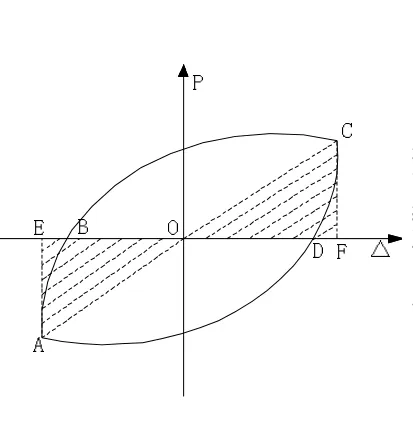
图9 能量耗散系数示意

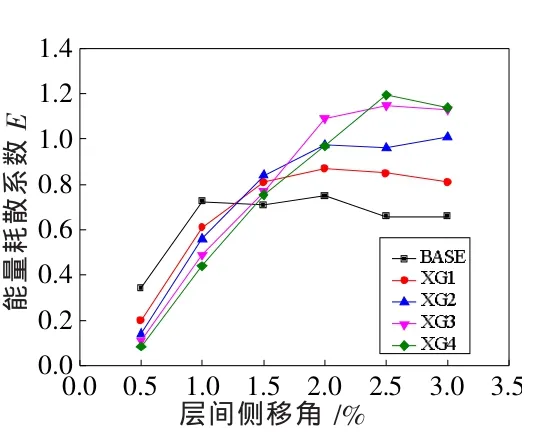
图10 试件能量耗散系数

3.4 骨架曲线

为直观比较结构的强度和延性的变化规律，给出XG系列试件的骨架曲线，如图11所示。骨架曲线是将滞回曲线中每一个循环所对应的峰值点数据依次连接绘制出的位移-荷载曲线。从图中可以看出，XG系列试件均在层间位移0.5%左右处达到了屈服强度，较早地进入塑性耗能，为结构提供可观的耗能能力。试件BASE、XG1、XG2随着层间位移角的增加，荷载呈现出不断增长的趋势，在极限位移3%处，荷载并未出现显著下降，说明试件在加载过程中保持着良好的延性，有利于结构吸收和耗散地震能量。试件XG3、XG4在位移达到2.5%处，荷载出现下降，这是由于钢板厚度增大时，两侧的加劲方管在加载后期不能有效地限制住钢板的面外变形。观察此骨架曲线还可以发现，随着钢板厚度的增加，相对应的屈服荷载和极限荷载都会随之增加，同时结构依然可以保持良好的延性性能。

3.5 承载力退化

在位移幅值不变的条件下，结构或构件的承载力随反复加载次数的增加而降低的特性称为承载力退化，承载力退化系数的定义见《混凝土结构试验方法标准》[11]（GB 50152-1992）。试验结构构件的承载力退化可用承载力降低系数表示，承载力降低系数应按下式计算

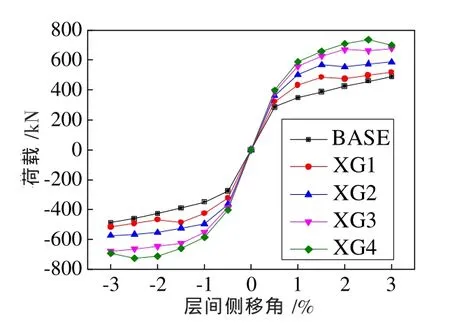
图11 XG系列试件骨架曲线

式中，Qij，min为位移延性系数为j时，第i次加载循环的峰点荷载值；Q1j，max为位移延性系数为j时，第1次加载循环的峰点荷载值。

图12给出了XG系列模型试件的承载力退化情况，观察可知在正向、负向加载过程中，XG试件的承载力退化曲线波动都相对较小，在0.9以上。

3.6 刚度退化

在位移幅值不变的条件下，结构或构件的刚度随反复加载次数的增加而降低的特性称为刚度退化，可取同级变形下的环线刚度K1表示。试验结构构件的刚度退化可用环线刚度[11]表示，环线刚度应按下式计算

式中，Qij为位移延性系数为j时，第i次循环的峰点荷载值；uij为位移延性系数为j时，第i次循环的峰点变形值；n为循环次数。

试件的刚度退化情况如图13所示。由图可知，模型试件在正负向加载过程中的刚度变换基本一致。在加载初期，刚度退化的幅度较大，随着位移的增大，刚度变化渐渐趋于平缓。

加载初期，蝴蝶形钢板剪力墙-自复位钢框架结构的刚度主要由蝴蝶形钢板剪力墙的刚度以及自复位框架的刚度组成；随着加载位移增大，钢板进入塑性，对整体结构的刚度贡献逐渐降低，最终结构的刚度完全取决于自复位钢框架。由图可以看出，在加载初期刚度中，外围自复位框架刚度仅仅占了20%左右，而剩下的80%由钢板提供，可见內填钢板剪力墙不仅起到了耗能作用，还可以为结构提供相当可观的抗侧刚度。

从图中也可看出，随着钢板厚度越厚，初始刚度越大，但是随着加载位移的增大，不同厚度试件的刚度差值越来越小，此时的刚度均来自于外围自复位钢框架。

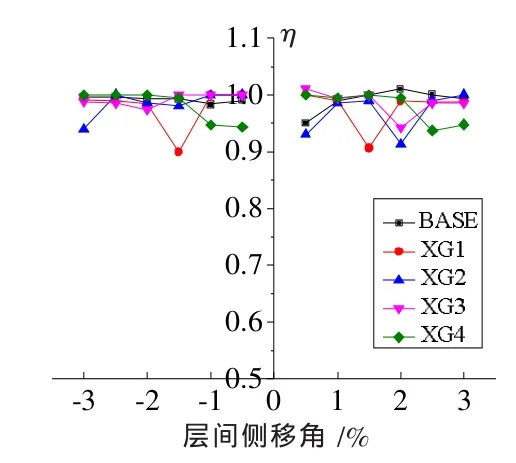
图12 XG系列试件承载力退化情况

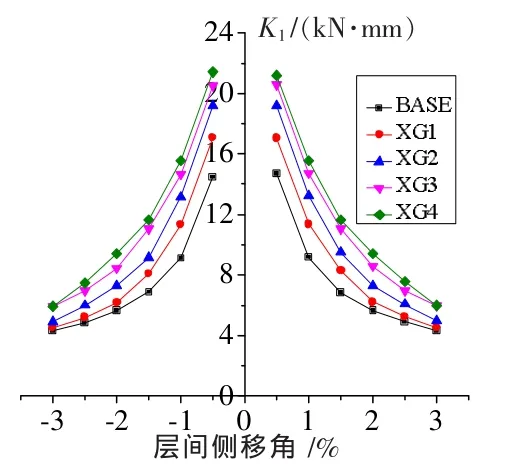
图 13 刚度退化曲线

4 结论

基于有限元软件ANSYS的验证模拟结果，分析了钢板剪力墙-自复位钢框架结构的强度、刚度、延性和复位性能，得出以下结论：

（1）相同循环荷载条件下，随着钢板厚度t的增加，极限承载力、初始刚度、能量耗散系数和残余层间位移角均随之增大，说明增加厚度改善了结构的承载力和耗能能力，但是削弱了结构的复位性能；

（2）在钢板两侧布置竖向加劲方管减小面外变形，对试件的刚度和稳定承载力的补强效果显著；

（3）经过合理设计和加工，选取合适的钢板厚度，在耗能理想的同时能达到预期的复位效果；

（4）钢板剪力墙-自复位钢框架结构综合了自复位结构及钢板剪力墙的优点，构造合理，以普通钢材及钢绞线为原材料，耗能性能好，抗震性能优越，具有良好的应用前景。

[1]潘振华.自复位钢框架节点有限元模拟及参数分析[J].建筑结构学报，2011，32（3）：35-42.

[2]RICLES J,SAUES R,GARlOCK M,et al.Posttensioned seismic-resistant connections for steel frames[J].J Struct Eng,2001,127（2）：113-121.

[3]GARLOCK M M，RICLES J M．Experimental studies of full scale posttensioned steel connections[J]．J Struct Eng，2005，131（3）：438-448.

[4]DOWDEN D M,PURBA R,BRUNEAU M.Behavior of self-centering steel plate shear walls and design considerations[J].J Struct Eng,2012, 38（1）：11-21.

[5]MA XIANG，ERIC BORCHERS，ALEX PENA，et al.Design and behavior of steel shear plates with openings as energy dissipating fuses[R].Stanford University,USA,2011.

[6]潘振华.具有自复位能力的钢框架体系研究[D].北京：清华大学，2010.

[7]徐基磊.利用开缝钢板剪力墙作为耗能元件的自复位结构体系研究[D].苏州：苏州科技学院，2014.

[8]中国建筑科学研究院.GB 50011-2010建筑抗震设计规范[S].北京：中国建筑工业出版社，2010.

[9]BALDVINS N,BERMAN J W,LOWES L N,et al.Development of damage prediction models for steel plate shear walls[J].Earthquake Spectra, 2012，28（2）：389-399.

[10]兰涛，郭彦林，郝际平，等.焊接应力对开洞钢板剪力墙极限承载力的影响[J].施工技术，2011（11）：62-65.

[11]中国建筑科学研究院.JGJ101-96建筑抗震试验方法规程[S].北京：中国建筑工业出版社，1997.

Seismic performance study of new shaped plate applied in self-centering steel frame

LI Qian,LI Qicai

（Jiangsu Key Laboratory of Structure Engineering,SUST,Suzhou 215011,China）

A new shaped steel plate wall is put forward to study the energy dissipation and self-centering capacity in self-centering steel frames.The configuration and mechanism of this new system are explained in detail. With the ANSYS software,five specimens in different thickness are simulated,and the hysteretic curve,the skeleton curve,the energy dissipation coefficient curve,the stiffness degradation curve and the bearing capacity degradation curve can be obtained.The parameter analysis of the strength,stiffness,ductility and recentering performance of the structure are carried out.The results show that stiffened square tubes on both sides can effectively restrain the out-to-plane deformation of specimens,ensuring that the frame has good recentering capacity. With the increase of plate thickness,the energy dissipation capacity and the loading capacity of the structure will be enhanced,but the recentering performance will be poor.

self-centering steel frame;infilled butterfly-shaped walls;ductility;hysteresis loop;coefficient of energy dissipation

TU391

A

2096-3270（2017）01-0001-06

（责任编辑：秦中悦）

2016－07-13

国家自然科学基金项目（51378326）；江苏省结构工程重点实验室开放课题（ZD1204）

李 乾（1991-），男，江苏盐城人，硕士研究生。

李启才（1969-），男，副教授，博士，从事钢结构的新型结构体系和抗震设计研究，Email：ustsgjg@163.com。