从电容器充、放电实验所想到的

杨 君

(北京教育考试院,北京 100083)

从电容器充、放电实验所想到的

杨 君

(北京教育考试院,北京 100083)

本文从教材中的实验“用传感器观察电容器的充电和放电”出发,通过定量计算,分析了电容和电感的充、放电过程,描绘了电容和电感在充放电过程中各物理量随时间的变化曲线,纠正了教材中不严谨的表述．

电容； 电感； 充电； 放电

1 问题的提出

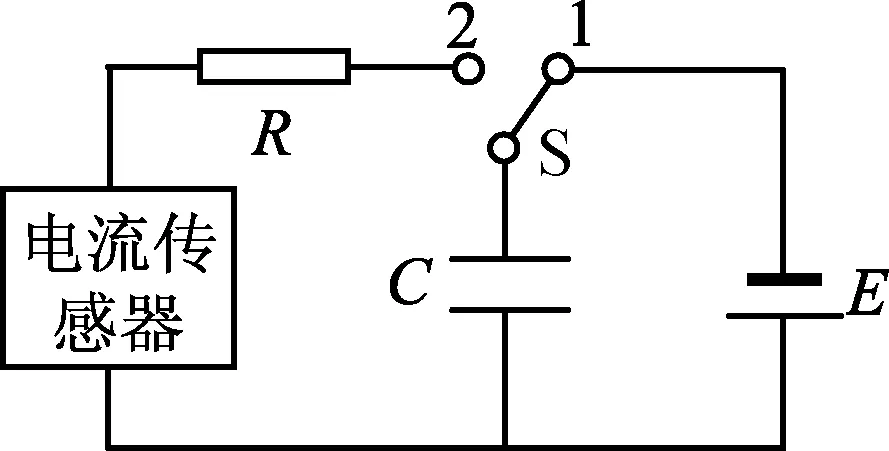
图1 观察电容器放电的电路图

人教版普通高中课程标准实验教科书物理选修3-1模块第1章“静电场”第8节“电容器的电容”节末有“做一做”实验“用传感器观察电容器的充电和放电”．具体细节如下:按照图1连接电路,电源用直流8V左右．电容器可选几十μF的电解电容器．先是开关S与1端相连,电源向电容器充电,这个过程可在瞬间完成； 然后把开关掷向2端,电容器通过电阻R放电,传感器将电流信号传入计算机,屏幕上显示电流随时间变化的I-t图像如图2所示．

图2 一个电容器放电的I-t图像

从教材原文可知,按照图示电路进行实验,电源向电容器充电过程可在瞬间完成;从图2所示的电容器放电过程可知,电容器放电过程持续时间长达4～5s,已不能算是瞬间完成了．而高中阶段普遍认为电容器的充、放电均在瞬间完成，这是怎么回事呢?本文拟对电容器、电感器的充放电过程进行定量计算,弄清楚电容、电感的充放电过程与哪些因素有关,充、放电过程所需时间的数量级为多少．

2 电容器的充、放电

如图1所示,取电源电动势为E,内阻为r．外接电阻阻值为R,电容器电容为C．设电容器的电压为UC,极板上的电荷量为q．下面分别讨论电容器的充、放电过程．

2.1 电容器充电(开关掷在1处)

由闭合电路欧姆定律有

ir+uC=E,

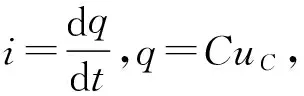
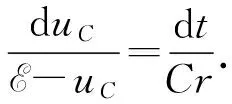
初始条件t=0时，uC=0，两端积分有

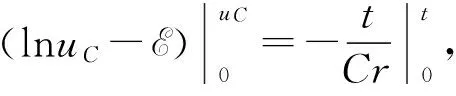
可得

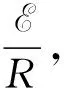
为直观地展现电容器充电过程中各物理量随时间的变化趋势,设电源内阻r=1Ω,电容C=400μF(与教材中的实验参数统一,具体计算见下文电容器的放电过程)．可分别画出电容器两端的电压,极板所带电荷量以及电路中的电流随时间变化趋势,如图3所示．图中纵轴中电压、电荷量和电流的最大值均统一为一个单位．可以看出,在上述参数下,如教材所言,电容器充电所需时间约为毫秒量级,可认为此过程在瞬间完成．

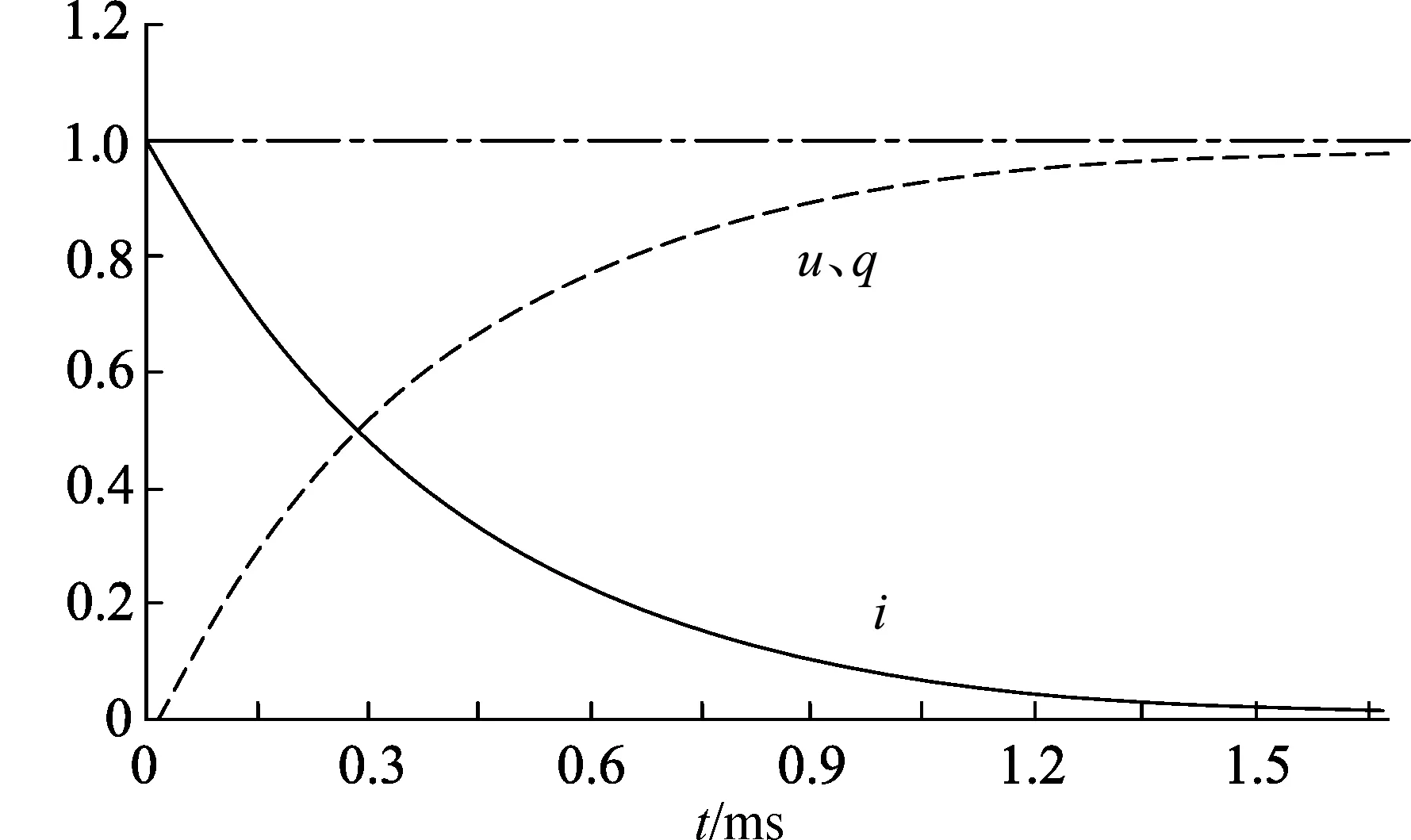
图3 电容器的充电过程

2.2 电容器放电(开关掷在2处)

由闭合电路欧姆定律得

iR+uC=0,

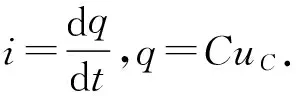
由上述表达式可知,与充电过程不同,放电过程中,电流、电压和电荷量的变化趋势相同,均随时间按指数函数递减,由初始时刻的最大值减小为放电完成时的0．从表达式也可看出,若C、R越大,各物理量随时间减小越缓慢,放电时间越长．

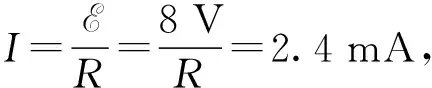
图4 电容器的放电过程

3 电感器的充、放电

类比电容器充、放电过程的计算,下面对电感器的充、放电过程进行讨论．

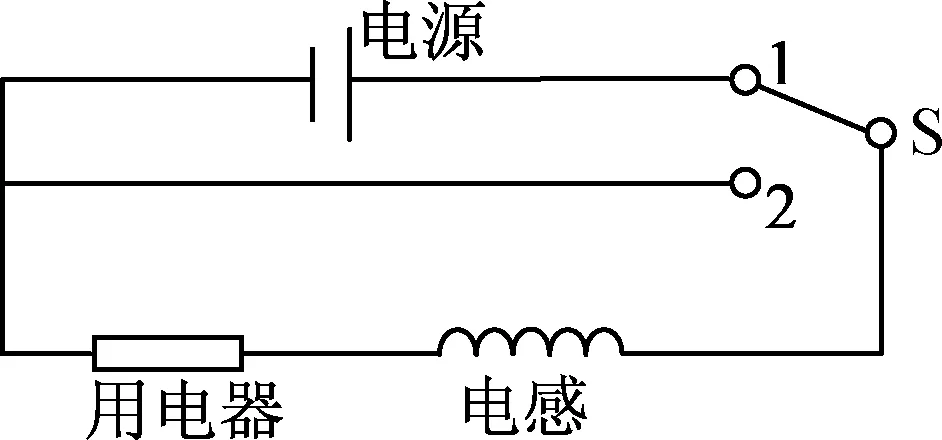
图5 观察电感器充、放电的电路图

如图5所示,取电源电动势为E,内阻为r．外接电阻阻值为R,理想电感器的自感系数为L．设流过电感的电流为i．下面分别讨论电感器的充、放电过程．

3.1 电感器充电(开关掷在1处)

由闭合电路欧姆定律得

简化并积分

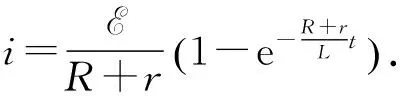
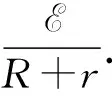
为直观地展现电感器充电过程中各物理量随时间的变化趋势,设电源内阻r=1 Ω(可忽略),R=1 kΩ,L=10-2H,可画出电感充电过程中的电流随时间变化曲线,如图6所示．图中纵轴中电流的最大值统一为一个单位．可以看出,在上述参数下,电感充电所需时间的数量级为10-5s,持续时间很短,可认为是在瞬间完成．

图6 电感器充电的I-t图像

3.2 电感器放电(开关掷在2处)

由闭合电路欧姆定律得

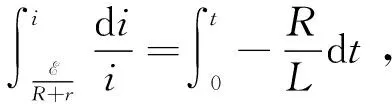
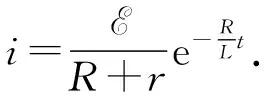
按照充电过程中设定的参数,并画出电感放电过程中的电流随时间变化曲线,如图7所示．与充电过程相同,放电所需的时间约为10-5s量级．可见,电感线圈的充、放电过程都是瞬时完成．在实验过程中,为延长充、放电时间,可适当减小R或增大L．

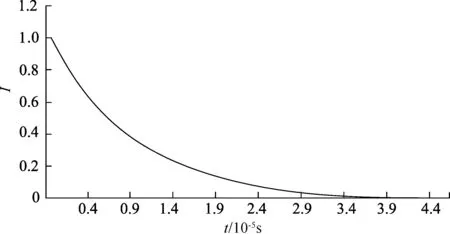
图7 电感器放电的I-t图像

4 总结

需要说明的是,上述分析是在理想情况下的推导,电容、电感均为理想电容器和电感线圈,与实际实验情境略有差异,但计算结果仍足以描述电容、电感充、放电过程．由分析可知,电容、电感在充放电过程中,所涉及到的电学量(电流、电压、电荷量)均随时间按指数函数变化,变化趋势的快慢与实验器材有关,取决于电容C,自感系数L和电阻R的大小．如电容器充电过程,若在充电电路中接入一阻值为几千欧的电阻,则充电过程持续时间达到几秒,并不是瞬间完成．

1 钟晓青.电容器充、放电演示实验的改进[J].物理教师，2012(3)：69.

2 邬夏波.电容器放电现象与C=Q/U关系实验的定量研究[J].物理教师，2010(5)：39，42.

2016-11-10)