基于武陵山片区产业结构的优化研究——以湘西州为例

陈望学，张琼枝，周慧婷，钱文舒

(吉首大学数学与统计学院，湖南吉首416000)

基于武陵山片区产业结构的优化研究
——以湘西州为例

陈望学，张琼枝，周慧婷，钱文舒

(吉首大学数学与统计学院，湖南吉首416000)

以湘西州为例通过灰色关联度分析说明了三大产业对经济增长的重要意义.接着建立回归方程，准确计量了各产业变动对经济增长的影响，并进一步从产业结构合理化、高级化和高效化三方面入手，构建产业结构优化评价指标体系，运用因子分析计算出了湘西州产业结构优化值.最后根据对湘西州的实证分析结果，提出了相应的政策建议，这对于武陵山片区内其他县市具有一定的现实意义和应用价值.

产业结构优化；灰色关联度分析；评价指标体系

1 实证分析

1.1 灰色关联度分析

经济增长与产业结构变动关系密切，产业结构随着经济增长和发展而变化，并且反过来作用经济增长.但不知道经济增长与产业结构之间的确切关系，因此用灰色关联理论对湘西州产业结构变动与经济增长的关联性进行分析[2].

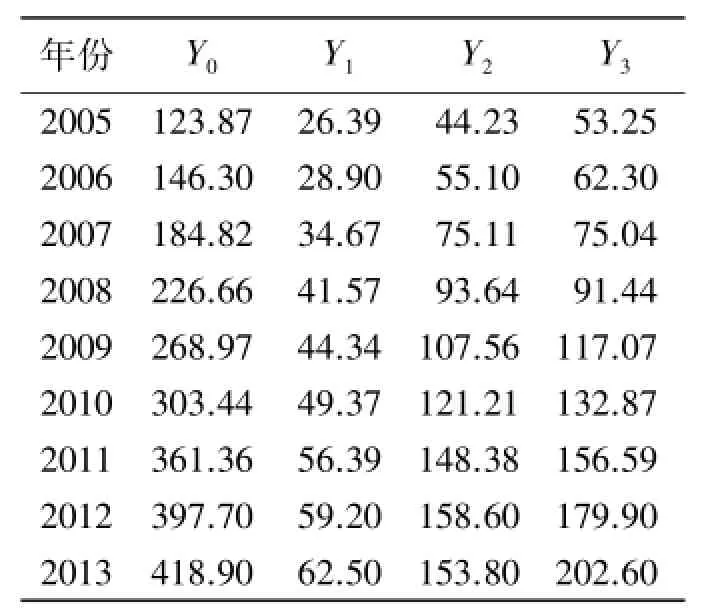
表1 序列数据表Tab.1 Sequential data

本文选取2005－2013年湘西州生产总值Y0(亿元)为参考序列，第一、二、三产业的增加值Y1、Y2和Y3(亿元)为比较序列进行灰色关联度分析，具体数据见表1.

首先将4个序列初始化，去量纲(每一列除以这一列的第一个数)，得到下列值:

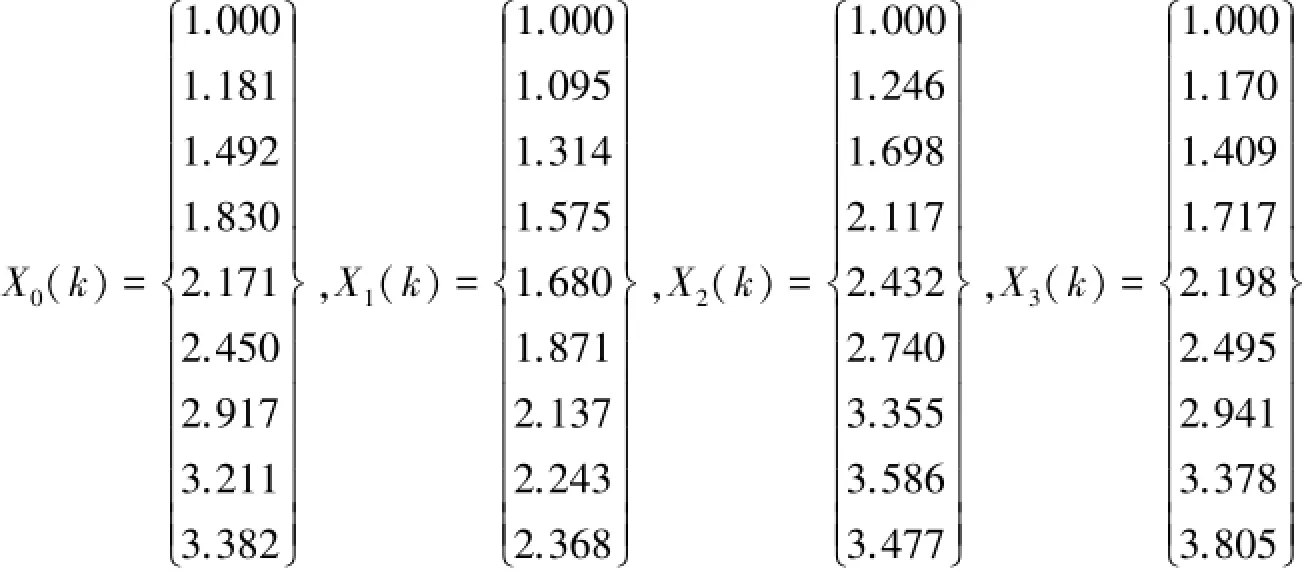
其中Xi(k)(i＝0，1，2，3)表示第i组序列第k年初始化后的值.接着计

算比较序列和参考序列差的绝对值作为绝对差序列，求得两级最小差和两级最大差分别为:

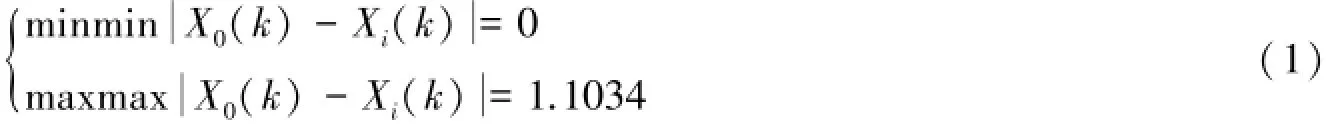
再根据式(2)计算第i组比较序列与参考序列的关联系数ηik():

该模块采用通用模块，对远程数据库进行动态监视，并根据预警管理模块中设定的预警规则，自动扫描并筛选出符合预警条件的数据。防旱监测预警系统中，所有对数据库的操作都是通过调用数据管理模块提供的公共方法，或是对公共方法的组合来完成的。该模块的特性是封装性强、安全性高、灵活性好。通过封装的数据库操作方法，只提供对外接口，使得结构统一，方便管理。通过对配置文件的修改与处理，可以灵活运用到不同数据库环境下的各种系统中。

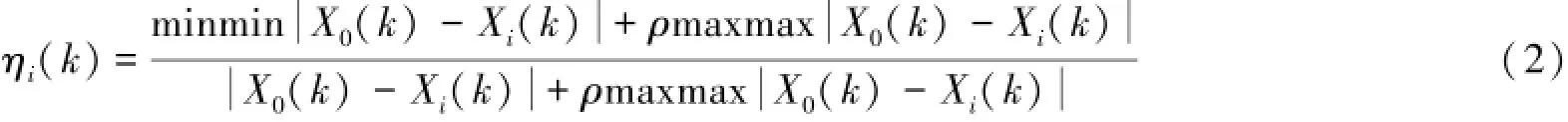
用Matlab求得关联系数如表2所示.

1.2 回归分析

灰色关联度分析只初步找出了经济增长与产业结构变动的密切程度，为了准确计量各产业变动对经济增长的影响，本文引入以下回归模型[3－6]:

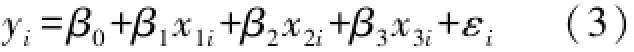
其中:yi表示第i年湘西州总产值增长率，x1i，x2i，x3i分别为第一、二、三产业增长率，β1，β2，β3分别表示当第一、二、三产业增长率变化一个单位时引起湘西州总产值增长率发生的变化，εi是随机干扰项，β0为常量.

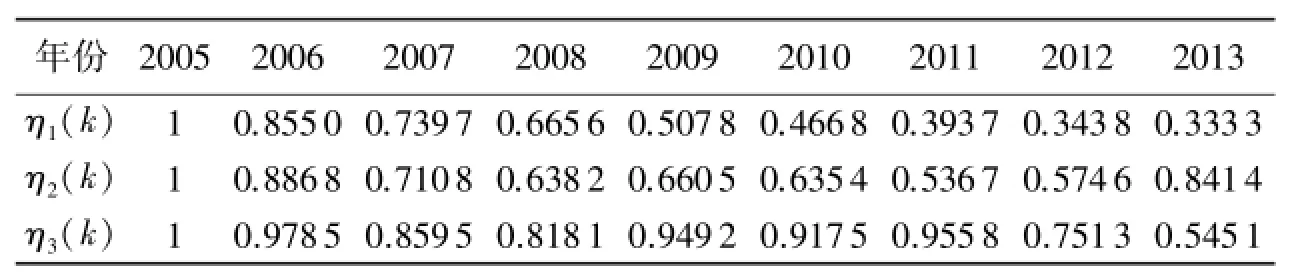
表2 关联系数Tab.2 Correlation coefficients

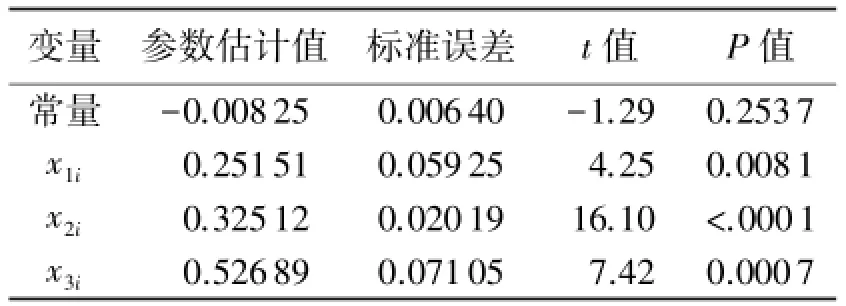
表3 参数估计Tab.3 Parameter estimator

表4 方差分析Tab.4 Variance analysis

用SAS软件对2005－2013年湘西州生产总产值增长率和第一、二、三产业增长率的数据做回归分析，输出参数估计表和模型检验结果如表3和表4所示.

根据表3的结果得到回归方程为:

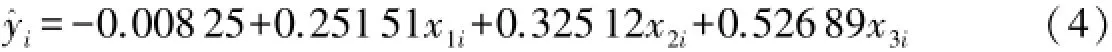
从表3也可知，当置信水平α＝0.05时，自变量的P值均小于0.05，表明三个产业对湘西州生产总值都有显著影响.表4显示F检验通过，且算得的复相关系数R2＝0.9977，这说明模型整体拟合的很好.

从式(4)可以看出，当第一、二、三产业的增长率分别增长1个单位，湘西州总产值增长率分别变化0.25151，0.32512，0.52689个单位，这表明湘西州第三产业对其经济的影响作用最为明显，第二产业次之，农业最小.近几年，湘西州经济快速发展，工业不再是主导产业，农业产值增长速度也较慢，这会阻碍湘西州经济持续快速增长.因此产业结构的调整迫在眉睫，而且应在农业上加大投入.

表5 特征值、贡献率、累计贡献率Tab.5 Eigenvalue，contribution rate，accumulation contribution rate

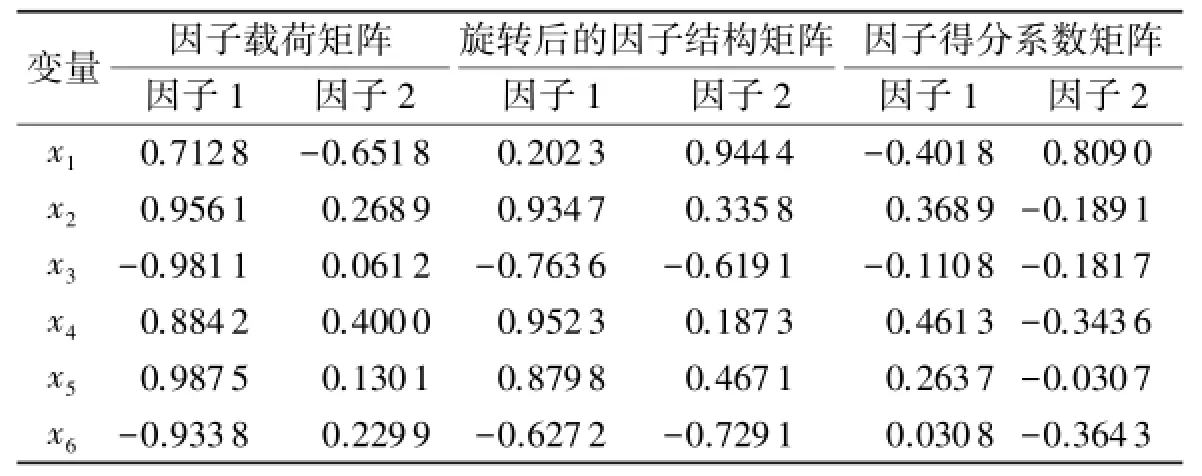
表6 因子载荷矩阵、旋转后的因子结构矩阵及因子得分系数矩阵Tab.6 Component matrix，rotated component matrix and component score coefficient matrix

2 产业结构优化测度

为了客观地反映湘西州产业结构优化的真实情况，本文依据产业结构优化内涵及评判标准，选取了衡量产业结构合理化的人均产值密度比x1和产业结构偏离度x2，衡量产业结构高级化的第三产业增加值占比x3和第三产业就业人数占比x4，以及衡量产业结构高效化的全社会劳动生产率x5和万元生产总值能耗x6六个指标[7]的2005－2013年的数据进行综合因子分析[8－12]评估，得到特征值、贡献率和累计贡献率如表5所示.从表5可以看到第一个因子的特征值为5.0137，累计贡献率83.56%.第二个因子的特征值小于1，贡献率也不大.但考虑到一个因子可能不好描述实际意义，因此提取前两个因子，使得累计方差贡献率达到95.74%.接着计算出因子载荷矩阵[13－14]、旋转后的因子结构矩阵和因子得分系数矩阵[15－16]如表6所示.

从因子载荷矩阵可以看出:第一主因子在x2、x3、x5和x6上均具有很大的载荷和解释能力，但是第二主因子没有起太大的解释作用，所以用方差最大旋转法得到旋转后的因子结构矩阵，相比旋转前的而言能更好地解释经济意义.从旋转后的因子载荷矩阵可以看出:第一主因子在x2和x4上具有很大的载荷和解释能力，这些变量包含了产业结构优化评价体系中高级化和高效化的指标，综合性强，第二主因子则在x1上具有很大的载荷和解释能力.根据表6中的因子得分系数矩阵可以写出以下的因子模型函数的表达式:

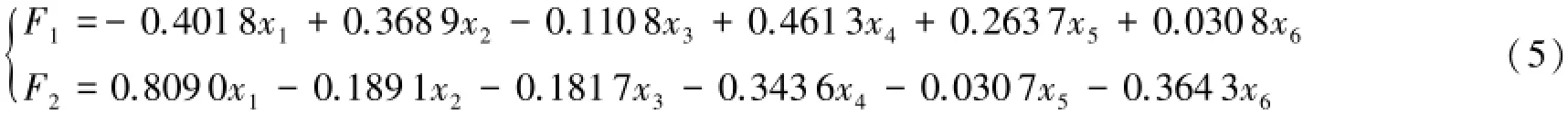
其中:F1表示第一个因子的因子得分，F2表示第二个因子的因子得分.

由表5可以得到两个主因子的方差贡献率分别为:0.8356，0.1218，以两个主因子的方差贡献率为权重，得到综合得分的计算方程:

将式(5)代入式(6)得产业结构优化值F为:

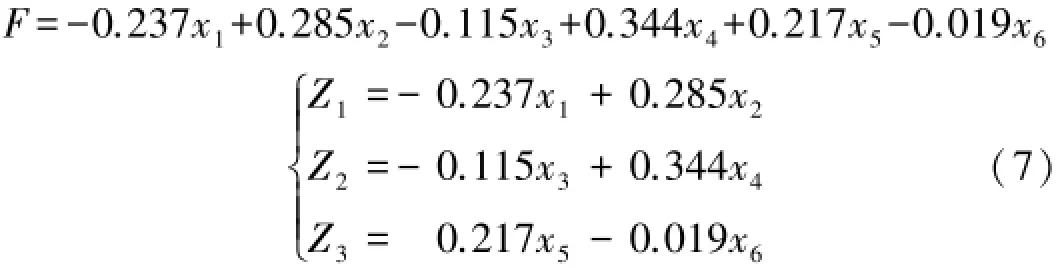
其中:Z1表示产业结构合理化得分值；Z2表示产业结构高级化得分值；Z3表示的是产业结构高效化得分值.通过式(7)的计算，可以得到湘西州2005－2013年产业结构优化评价的得分值如表7所示.

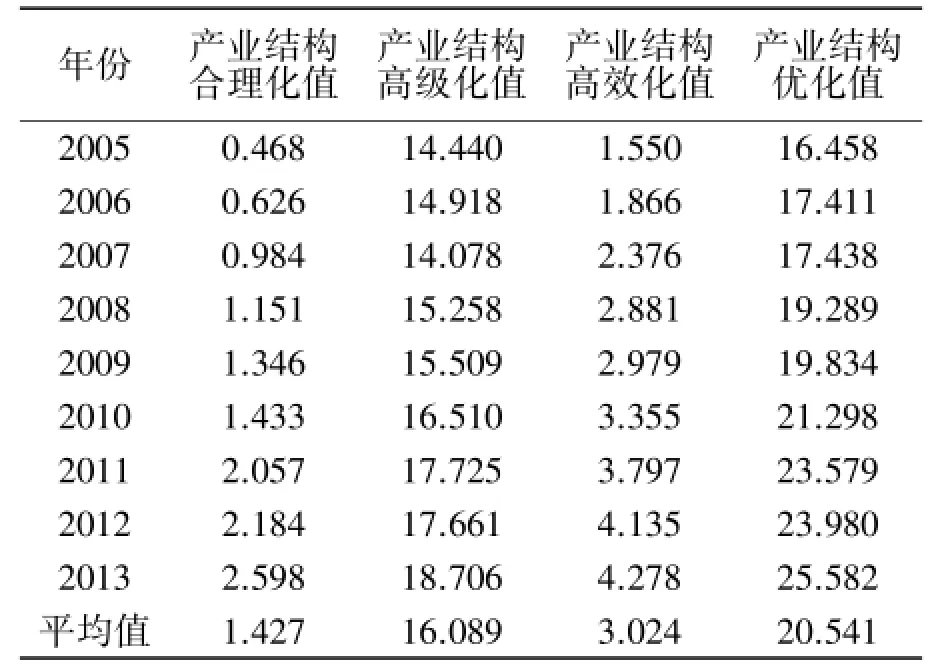
表7 产业结构优化评价的得分值Tab.7 Industry structural optimization value

从表7可以看出，湘西州产业结构优化评价的得分值基本呈现逐年上升的趋势，这与湘西州经济发展状况相符，说明该指标体系所计算得到的优化值符合实际经济情况.从数据上看2009年以前，产业结构合理化值、产业结构高效化值和产业结构高级化值都低于平均水平，影响了整个产业结构的优化.但在2010年后，产业结构高级化、产业结构高效化和产业合理化水平都有所提升，且产业结构优化值首次超过平均水平.

由式(7)可知，产业结构偏离度对产业结构合理化影响最大，它每变动一个单位，合理化得分值变动0.285个单位；而人均产值密度比的系数为负，它每变动一个单位，合理化得分值减少0.237个单位.产业结构高级化则主要受第三产业就业人数占比的影响，它每变动一个单位，高级化得分值变动0.344个单位；而第三产业增加值占比每变动一个单位，高级化得分值减少0.115个单位.产业结构高效化得分由全社会劳动生产率和万元生产总值能耗决定，它们每变动一个单位，高效化得分值分别变动0.217、－0.019个单位.

对照时间序列趋势和内部指标影响的分析，可以看出要优化产业结构，就必须从合理化、高级化、高效化三个方面来考虑.合理化要求湘西州经济发展达到全国平均水平且就业结构和产业结构相协调.高级化则是第三产业的发展力度要加强.高效化是指劳动力及能源等资源的高效利用.因此湘西州在提高经济总体水平的增加产值的同时，要协调人文环境使产业结构不断优化.

3 总结与建议

本文从产业结构与经济增长的关联度分析出发，发现了湘西州产业结构优化水平与全国平均水平存在一定差异，然后基于因子分析得出了产业结构优化的评价标准以及优化的方向.对此，提出以下建议:

1)湘西州位于武陵山片区的腹地，是湖南省西部的一个民族地区，也是湖南省唯一一个被列入西部大开发的城市，因此湘西州应抓住西部大开发的机遇，争取国家对湘西州区域内部的基础设施建设、公共物品的供应以及教育科技投入等，以改善区域投资环境.

2)产业结构优化不仅体现在三次产业之间，也表现在三次产业内部的发展水平.通过回归分析我们知道，对湘西州经济影响最大的是第三产业，而第三产业中旅游业所占比重过大，所以在加大对第三产业的投入，继续做强做大现有优势产业的同时，还要重点优化产业内部结构，使各个产业之间呈均衡发展.

3)增加产业间的关联效应，带动相关产业的发展.对于第一产业，加大林业资源及农产品的开发；对于第二产业，除了保持目前的工业结构外，还需要加大对优势矿产资源的深度加工(如湘西州花垣县的锰)，延长产业链条；对于第三产业，除了继续发挥旅游资源的优势外，还需要调整好与之配套的相关产业的发展，优化第三产业的内部结构，更好的开发州域内的优势资源来推动经济的发展.

[1] 周中林，郭荣鑫.武陵山片区经济发展实践及策略选择——基于西部大开发新时期战略机遇[J].特区经济，2011(4):221－223.

[2] 李懿洋.甘肃省产业结构与经济增长的灰色关联分析[J].企业经济，2011(5):20－23.

[3] 陈玲.西部地区产业结构水平和效益分析[J].统计与信息论坛，2003，18(5):77－79.

[4] 张玉哲.产业结构与经济增长的统计研究[D].厦门:厦门大学，2001.

[5] 李子奈.计量经济学应用研究的总体回归模型设定[J].经济研究，2008(8):136－144.

[6] 张维迎，周黎安，顾全林.高新技术企业的成长及其影响因素:分位回归模型的一个应用[J].管理世界，2005(10):94－101.

[7] 康艳芳.河南省产业结构调整实证预测分析[J].统计与决策，2013(21):143－145.

[8] 陈望学，李洋阔.因子分析的一个简单应用[J].考试周刊，2016(4):167－168.

[9] 罗世家.影响薇菜生长的主要环境因子分析[J].湖北民族学院学报(自然科学版)，2001，19(4):8－10.

[10] 陈彩霞，林建生.重庆市生态环境质量综合评价研究[J].湖北民族学院学报(自然科学版)，2006，24(4):348－351.

[11] 赵小娜，李大威，高然，等.延吉市城市自然生态安全评价[J].延边大学农学学报，2016，38(2):109－116.

[12] 刘宗鑫，王广杰，王群，等.基于因子分析和灰色关联度分析的区域可持续发展能力建设研究——以四川省为例[J].安徽农业科学，2015，43(1):376－380，383.

[13] 王巧英.因子分析法中因子载荷矩阵的应用——内蒙古地级市居民生活质量的综合评价[J].统计教育，2009(12):49－53.

[14] 马庆华，李永红，梁丽松，等.冬枣优良单株果实品质的因子分析与综合评价[J].中国农业科学，2010，43(12):2491－2499.

[15] 纪荣芳.城市居民消费结构的因子分析模型及应用[J].山东农业大学学报(自然科学版)，2007，38(2):273－276.

[16] 郭武，李轶杰，戴礼荣，等.说话人识别中的因子分析以及空间拼接[J].Acta Automatica Sinica，2009，35(9):1193－1198.

责任编辑:时 凌

Research on Optimization of Industrial Structure Based on Wuling Mountain Area——Take Xiangxi Prefecture as An Example

CHEN Wangxue，ZHANG Qiongzhi，ZHOU Huiting，QIAN Wenshu
(College of Mathematics and Statistics，Jishou University，Jishou 416000，China)

Taking Xiangxi Prefecture as an example，this paper illustrates the importance of the three industries to economic growth through grey relational analysis.And then a regression equation is established to accurately measure the impact of industrial changes on economic growth，and an evaluation index system of the industrial structure optimization is constructed from rationalization，upgrading and efficiency of industrial structure.The factor analysis is used to calculate the optimization value of industrial structurein Xiangxi Prefecture.Finally，according to the empirical analysis results，we put forward corresponding policy suggestions，which has some practical significance and reference for other cities/counties of Wuling Mountain Area.

industrial structure optimization；grey relational analysis；evaluation index system；factor analysis

TP182

A

1008－8423(2017)01－0107－04

10.13501/j.cnki.42－1569/n.2017.03.024

2016－11－16.

国家自然科学基金项目(11461027)；湖南省研究生科研创新项目(CX2016B616)；湖南省大学生研究性学习和创新性实验项目(湘教通[2016]283号)；吉首大学本科生校级科研项目(JDX16025).

陈望学(1985－)，男，博士，讲师，主要从事经济统计与统计计算的研究.