一类广告的随机最优控制模型的奇摄动解
2017-04-13包立平
王 攀,包立平
(杭州电子科技大学大学理学院,浙江 杭州 310018)
一类广告的随机最优控制模型的奇摄动解
王 攀,包立平
(杭州电子科技大学大学理学院,浙江 杭州 310018)
讨论随机情形下广告投入的最优控制问题,应用最优控制原理得到关于广告投入的奇异摄动随机最优控制问题的HJB方程,利用奇摄动渐近展开的方法得到HJB方程的形式渐近解,并得到其一致有效估计.
广告投入;最优控制;奇摄动;形式渐近展开;一致有效估计
0 引 言
广告的最优投入问题由于其实际的意义而引起了人们的广泛关注,得到了大量的研究.文献[1-2]建立了关于广告的控制模型,并应用了最优控制原理对模型进行求解,但较少考虑随机因素对广告投入的影响,仅建立了关于简单随机变量的数学模型.文献[3]介绍了时滞随机最优控制问题的最大值原理,并应用其原理解决了生产消费问题,但未求出模型的一般解.本文考虑了一类具有弱随机干扰的广告-销售反应模型,在研究的过程中发现,相应的HJB方程的系数出现不连续情形,该问题又涉及到当前热门的奇异摄动理论中不连续系数问题,从而形成奇异摄动问题中一类既有意义又困难的题目,文献[4-8]对此类问题中的一些模型进行了研究.本文应用随机最优控制原理得到关于广告投入的微分方程,利用奇异摄动渐近展开的方法得到广告投入的形式渐近解,最后给出了一致有效估计,为实际的广告决策提供了数学工具.
1 模型建立
设x满足如下的随机微分方程:
dx=[ρμ(1-x)-δx]dt+εσdω
(1)
其中,x为产品在整个潜在市场中所占据的份额,ρ为广告反应常数,μ为广告投入率,δ为衰退常数,σ为风险因子,ω为标准的Brown运动,ε>0为小参数.
模型(1)的最优控制问题的目标函数是

(2)
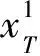
上述最优控制的哈密尔顿函数为H=e-rt(αx-μ)+Vxf,其中f=[ρμ(1-x)-δx],
则上述问题的最优均衡控制策略为
(3)
(4)
式(1)和式(2)的HJB方程[9]为
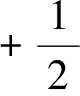
(5)
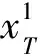
(6)
(7)
2 形式渐近展开

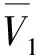

(8)
则上述方程组容易解得
(9)

(10)
ΠV1N=CΠNeλ1ρ1,(N≥0)
(11)

从表1可以看出,在扭动运动阶段GMs评估为PR的早产儿发展为行为多动冲动或攻击性行为等行为障碍性疾病的比例较高,尤其是在扭动阶段连续出现PR,后期发展为多动冲动或攻击性行为的比例较高,而在足月后扭动阶段前转归成N的早产儿,发展)成为多动冲动或攻击性行为的比例低。
RV1N=CRNeλ2ρ2,(N≥0)
(12)

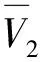

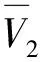
(13)
(14)
(15)
下面来确定上述解中的常数.
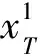
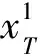
由上式及式(9),式(11)可解出CΠ0.



此时,V10,V20中的所有常数已确定.重复上述步骤可得解中的所有常数.
3 一致有效估计

(16)

证明 分别将式(16)代入式(6)、式(7)中第1式得:

(17)

4 结束语
本文建立了关于广告投入的随机最优控制模型,应用随机最优控制原理得到最优广告投入的微分方程.该微分方程其系数出现不连续的情形,这成为本文研究的一个难点.本文首先将原问题分解为两个不同的部分,分别应用奇异摄动渐近展开的方法得到形式渐近展开式,再应用匹配法进行连接得到原问题的形式渐近展开式,然后根据最大值原理得到了上述形式渐近解的一致有效性.从而得到了模型的求解方法,这为实际的广告决策提供了数学工具,对进行销售管理有一定的指导意义.
[1]席酉民,陆晓鸣.广告的动态最优控制模型[J].系统工程理论与实践,1998,18(08):11-18.
[2]王秀青,蔡立军.竞争环境下的广告策略研究[J].纺织高校基础科学学报,2009,22(3):404-408.
[3]陈丽.时滞随机系统的最优控制问题及应用[D].济南:山东大学,2010.
[4]丁海云,倪明康.函数不连续的二阶拟线性奇摄动边值问题[J].纯粹数学与应用数学,2010,26(5):768-775.
[5]丁海云,倪明康.具有不连续源的奇摄动边值问题[J].数学杂志,2012,32(6):1121-1128.
[6]WULM,NIMK,LUHB.Step-likecontraststructuresofsingularlyperturbedoptimalcontrolproblem[J].JournalofComputationalMathematics, 2012,30(1): 2-13.
[7]WULM,NIMK,LUHB.Internaltransitionlayersolutionofsingularlyperturbedoptimalcontrolproblem[J].ActaMathematicaScientia, 2013,33(2):206-215.
[8]ZHANGY,NAIDUDS,CAICX,etal.Singularperturbationsandtimescalesincontroltheoriesandapplications:onoverview2002-2012 [J].InternationalJournalofInformationalandsystemssciences, 2014,9(1):1-36.
[9]SCHMIDLIH.StochasticControlinContinuousTime[M]//StochasticControlinInsurance.London:Springer, 2008:27-111.
Singular Perturbation Solution of a Class of Stochastic Optimal Control Model for Advertising
WANG Pan, BAO Liping
(SchoolofScience,HangzhouDianziUniversity,HangzhouZhejiang310018,China)
A class of stochastic singular perturbation optimal control problem is discussed in this paper. Using the Kolmogorov equation, Hamilton-Jacobi-Bellman equation of the stochastic singular perturbation optimal control problem for advertising investment is achieved. Using the singular perturbation asymptotic expansion method, the formal asymptotic expansion is obtained. And the uniform valid estimation of the formal asymptotic expansion is derived.
advertising investment; optimum control; singular perturbation; asymptotic expansion; uniformly valid estimation
10.13954/j.cnki.hdu.2017.02.022
2016-06-15
王攀(1990-),女,山西朔州人,应用微分方程.通信作者:包立平副教授,E-mail:baolp@hdu.edu.cn.
O175.2
A
1001-9146(2017)02-0099-04
