灰色Verhulst与等维新息组合模型在中长期负荷预测中的研究
2017-04-12林天祥
林天祥 张 宁
(福州大学,福州 350116)
灰色Verhulst与等维新息组合模型在中长期负荷预测中的研究
林天祥 张 宁
(福州大学,福州 350116)
本文针对中长期电力负荷预测使用的历史数据较少且影响因素较多的特点,提出了一种线性灰色组合模型。该模型将灰色Verhulst模型与等维新息灰色理论线性组合,充分发挥了灰色Verhulst模型所需数据少、不受特定负荷数据以及等维新息灰色理论影响,保持数据原有维数、保证最优信息量和动态预测的优势。算例结果表明,该预测模型精度较高,具有实用性。
灰色Verhulst模型;等维新息灰色理论;组合负荷预测
电力负荷预测是电力系统规划、扩容、检修的基础,直接影响电网安全与地区经济。电力负荷预测大致分为3类,即长期负荷预测、中期负荷预测和短期负荷预测。与短期负荷预测相比,中长期电力负荷预测具有数据量较少,负荷数据受季节性、政治、经济等多方面因素影响的特点[1],电力负荷分布难以找到良好的分布规律。灰色预测的数据通常是较为杂乱且无直接规律可寻的,这些数据受到外界影响因素较多,所以显得毫无章法,但也使这些数据产生了潜在的联系,灰色预测正是找出这些联系,并且通过这些联系在数据之间构成一定规律。但由于GM(1,1)(灰色模型的一阶一个变量的灰微分方程模型。)模型是一个指数函数,只能描述单调的变化过程[2]。在中长期负荷预测中,当数据增长速度过快时,预测精度降低,而灰色Verhulst模型[3]本质上是GM(1,1)幂模型中指数为2的特殊情况,所以当数据增长过快时,该模型依旧可以保持较好的预测精度。等维新息灰色理论模型应用的是新陈代谢技术,去掉最老数据,加入最新数据,保持序列维数,保证了数据最优,故预测精度较高。因此,本文提出了一种基于灰色Verhulst模型与等维新息灰色理论的线性组合预测模型。该线性组合模型的优势不在于单个年份的预测或者最小误差的比较,而在于规避单个预测方法产生的偏离实际值过多的数据所产生的风险,以及在预测多个年份后的平均预测精度要优于单个预测模型的优点。Bates和GraIlger曾证明了2种或2种以上无偏的单项预测可以组合出优于每个单项的预测结果,从而有效地提高预测精度[4]。通过实例的验证,表明该组合模型的平均预测误差小于单一模型的平均预测误差,降低了预测风险,提高了预测精度。
1 灰色Verhulst模型
设原始数据序列为X(0)=(x(0)(1),x(0)(2),…,x(0)(n)),X(0)1-AGO累加序列为X(1)=(x(1),x(2),…,x(1)(n)),其中

Z(1)为X(1)的均值序列:Z(1)=(z(1)(2),z(1)(3),…,z(1)(n))。其中:

灰色Verhulst模型为
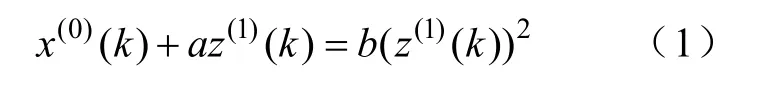
灰色Verhulst模型的白化方程为

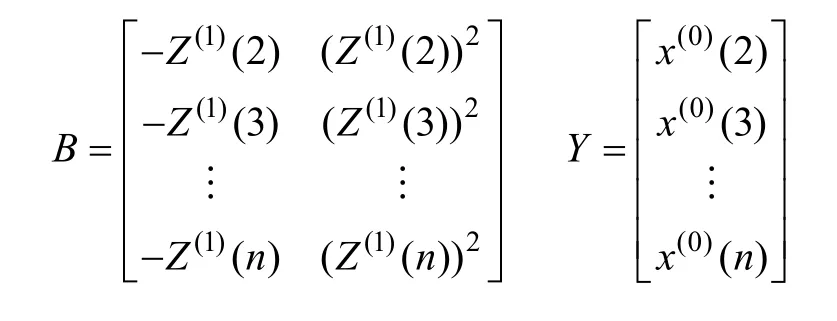
灰色Verhulst模型的解为

灰色Verhulst模型在中长期负荷预测中具有以下不足[5]:首先,灰色Verhulst模型要求负荷数据序列呈现饱和发展的过程,该模型需要呈现S曲线发展的数据,故通常情况下灰色Verhulst模型的预测数据也会呈S曲线的趋势。而在现代经济高速发展以及电力需求越来越多的情况下,中长期其实很难出现S型的负荷数据。中长期负荷数据的特征一般显示为逐年增高,所以灰色Verhulst模型预测上会产生偏差。
2 等维新息灰色理论
等维新息灰色处理是利用建立的GM(1,1)[3]模型进行数据上的新陈代谢。即通过一组数据序列进行灰色预测得到一个预测值,然后把得到的预测值加到这组数据序列的尾端,同时删除这一组数据序列的第一个数据,保持数列的个数不变,再建立GM(1,1)模型预测下一个值。又将这个预测得到的值加入数列末尾,同时删除最旧的一个数据,如此不断地加入新数据,删除老旧数据。
设原始序列是,X(0)=(x(0)(1),x(0)(2),…,x(0)(n)),X(0)的1-AGO原始序列X(1)=(x(1)(1),x(1)(2),…,x(1)(n)),由一阶灰色模型X(1)构成的微分方程为

式中,a和u为待定参数。将式(1)离散化得到矩阵形式,即

对方程式(5)按最小二乘法得


则微分方程的模拟值为x(0)(k)模拟值为

图1所示是等维新息灰色模型流程图。

图1 等维新息灰色模型流程图
3 线性组合预测
基于灰色Verhulst理论与等维新息灰色理论的组合预测模型就是将灰色Verhulst模型与等维新息灰色模型进行线性组合,构成一个组合模型。灰色Verhulst模型在中长期负荷数据偏少,在其他因素不确定的情况下,根据数据之间存在的隐含关系与潜在规律,建立较强的具有规律性的序列,尤其在数据分布呈S型曲线时,预测精度较高。但是灰色Verhulst模型受到数据类型限制的缺陷十分明显,并且在一些不定因素干扰,导致数据突然增大的情况下,就容易导致预测精度降低。而等维新息灰色的预测模型是将新陈代谢技术与灰色理论相结合产生的动态预测模型。该模型通过不断的产生新数据,剔除陈旧数据,保持了数据精度的可靠性,能很好地规避一些因不确定因素产生的特殊数据点对整个序列的影响。但等维新息灰色模型由于维数固定且不断剔除较老的数据加入新数据,使得固定维数内的数据变化呈单调递增。而在一些呈现特定曲线的数据条件下,例如S型曲线变化的数据条件下,在数据收尾处,S型曲线的数据趋于平缓,而等维新息的数据仍然呈现之前数据的递增情况,会导致预测数据精度的降低。
因此,本文将灰色Verhulst模型与等维新息灰色模型相结合,利用等维新息灰色模型规避特殊数据干扰的优点弥补灰色Verhulst模型受特殊数据干扰导致精度降低的缺陷;利用灰色Verhulst模型在S曲线下预测精度较高的特点,改善等维新息灰色模型受维数限制而在特定曲线下预测能力降低的情况。虽然两种预测模型在实际中的预测精度都较高,且平均误差偏低,但是也存在极个别预测点的预测误差偏高的情况,在实际中这种个别预测点误差偏高的情况,对电力系统的中长期规划具有不利影响。针对这种情况,本文合理地利用线性组合法,将两种方法线性组合,构成新的预测模型。
组合方法采用线性组合法[6],具体为
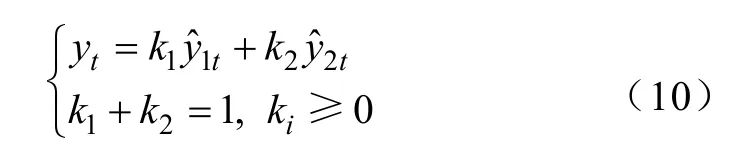
式中,1t、2t分别为灰色Verhulst模型和等维新息灰色理论模型的预测值;k1、k2为权重系数;yt为组合预测值。设有m个预测样本,为第i种预测模型第t个样本的拟合预测值,Yt为第t个样本的实际值,其预测的绝对误差为

令et=yt-Yt,则有

权重系数k1、k2,由平方和误差最小来求,其表达式如下

权重系数的求解用下列模型

式中,RT=[1,1],ki≥0(i=1,2)。对上式用拉格朗日乘子法求解,得

具体线性组合步骤为。
1)列出原始序列。
2)对原始序列进行灰色Verhulst模型预测,记录预测值ˆ1t。
3)对原始序列进行等维新息灰色预测,记录预测值2t。
4)将已经测出的1t、2t与实际值Yt代入式(14)中,求得权重系数k1、k2。
5)将k1、k2、1t、2t代入式(10)中,求出组合预测值。
6)数据检验,误差分析。
4 算例与分析
实例中采用的是福建省某地区1994—2003年的实际用电量为原始数据,再建立灰色Verhulst模型、等维新息灰色理论模型以及它们的组合模型进行预测。3个模型的预测结果见表1。灰色Verhulst模型、组合法、等维新息灰色模型与实际值从1998年到2002年的预测值曲线图如图2所示。

表1 三个预测模型的拟合结果

图2 灰色Verhulst模型、组合法、等维新息灰色模型预测值与实际值对比曲线图
从表1可以看出,组合法的相对误差始终小于灰色Verhulst模型与等维灰色模型中的最大相对误差,可以很好的规避风险,这是线性组合法的优点。并且组合法的平均相对误差为3者中最小,表示组合法的准确度最高,有较强的实用性。表1中,灰色Verhulst模型占组合法的权重系数最低,为0.1464,表明灰色Verhulst模型相对于等维新息灰色模型(权重系数:0.8536)精度偏低。因而组合预测的相对误差与等维新息灰色模型较为接近。
从图2中可以发现,组合法的预测值始终在灰色Verhulst模型预测值与等维新息灰色模型预测值之间,这是线性组合法的特点,可以很好地保证预测值的相对误差小于另外两种模型的最大相对误差,能较好的规避风险。例如,1999年的灰色Verhulst模型的预测值在图2中与组合法、等维新息灰色模型的预测值有较大偏差,查表一后发现灰色Verhulst模型预测值在1999年的相对误差高达5.08%,而组合法只有0.87%。在图2中组合法预测值与等维新息灰色模型预测值较为接近,是因为等维新息灰色模型在此算例中预测精度较高,因而在组合法的权重系数也较高,高达0.8536,这也是组合法的优点,即预测数据趋于较优模型。
从图2中可以发现,组合法的预测值与实际值没有较大偏差,组合预测值的波动是趋近于实际值的。从图2中可以看出,无论是总体走向还是局部范围,组合预测法的预测值相对于实际值的误差都是非常小的。
5 结论
本文采用组合预测的方法来实现中长期负荷预测,利用灰色Verhulst模型与等维新息灰色理论线性组合的方法,既能合理利用灰色Verhulst模型来应对中长期不定因素过多,数据偏少的情况,又能很好地结合等维新息灰色理论来改善数据精度,并且两种方法采用线性组合的形式,更好地规避了单一预测方法的风险,且提高了预测精度。实例表明,此预测方法具有实用性与可行性。
[1] 牛东晓. 电力负荷预测技术及其应用[M]. 北京: 中国电力出版社, 1998.
[2] 刘思峰. 灰色系统理论及其应用(Grey system theory and application)[M]. 北京: 科学出版社, 1999.
[3] 邓聚龙. 灰理论基础[M]. 武汉: 华中科技大学出版社, 2002.
[4] Bates J M, Granger C. The combination of forecasts[J]. Journal of the Operational Research Society, 1969, 20(4): 451-468.
[5] 张宁, 黄伟琼. 基于马尔科夫链改进无偏灰色Verhulst的中长期负荷预测模型[J]. 南昌大学学报(工科版), 2015, 37(4): 396-399, 404.
[6] 马永开, 唐小成. 线性组合预测模型优化问题研究[J]. 系统工程理论与实践, 1998(9): 10-114, 123.
Research on Grey Verhulst and Equal Dimension New Information Model in Medium and Long Term Load Forecasting
Lin Tianxiang Zhang Ning
(Fuzhou University, Fuzhou 350116)
The paper proposes a linear grey combined model for the medium and long term power load forecasting which has the characteristics of less historical data and more influencing factors.The model is a linear combination of the grey Verhulst model and the equal dimension new information grey theory.The model gives full play to the advantages of the grey Verhulst model which needs less data and is not affected by the specific load data.The model also takes advantages of the equal dimension new information grey theory ,which can maintain the original dimension of the data,guarantee the optimal information quantity,achieve dynamic prediction.The results show that the model has high accuracy and practicability.
gray Verhulst model; equal dimension new information grey theory; combined load forecasting
