近场空间LEMP波形特征研究

王李鹏 陈亚洲 万浩江 王晓嘉

（军械工程学院静电与电磁防护研究所，石家庄 050003）

近场空间LEMP波形特征研究

王李鹏 陈亚洲 万浩江 王晓嘉

（军械工程学院静电与电磁防护研究所，石家庄 050003）

为了进一步探索近场区空间雷电电磁脉冲场的波形特征，对近场区空中不同高度处的雷电电磁场与回击通道底部电流之间的相互关系进行了理论研究。基于TL模型，通过理论推导得到了近场区空间LEMP和回击电流之间的关系。对比电磁场精确表达式与其两级近似表达式的波形，结果表明：在距回击通道50m以内、高度为几十米到几百米的空间内水平电场的精确波形与其两级近似波形基本重合；在距离回击通道200m以内、离地高度500m以下的空间内角向磁场的精确波形与其两级近似波形基本重合。

雷电电磁脉冲场；回击通道底部电流；近场；精确波形；近似波形

雷电是大自然中最常见的一种电磁脉冲危害源[1-3]。闪电发生时，回击通道中上万安培的回击电流以与光速等数量级的速度向上传播，在回击通道及其周围产生强烈的热效应和雷电电磁脉冲（lightning electromagnetic pulse, LEMP），对人们日常电子电气设备及我军武器装备系统构成了严重的威胁，因此国内外许多学者对LEMP进行了大量的研究[4-8]。

关于雷电电磁脉冲场与回击电流之间的相互关系，Uman等人基于垂直通道证明了通道底部电流与电磁场在地表远场区的近似性[9]；军械工程学院陈亚洲教授从理论上研究了垂直通道下地表近场区通道底部电流与雷电电磁场的近似关系[10-13]；Leteinturier等人通过人工引雷实验实测到了近区雷电电磁场与底部电流波形之间的近似特性[14]。此外，在广东从化、山东等雷电试验基地，通过人工引雷实验也观测到了近区雷电电磁场与通道底部电流波形之间的近似关系[15-16]，如图1所示。这些观测结果为学者们深入研究雷电电磁场与回击通道底部电流波形之间的近似关系提供了数据支撑。

但是以上研究均是针对地表LEMP展开的，为进一步了解空间LEMP与回击电流波形之间的相互关系，本文将基于垂直通道模型研究近场区空间雷电电磁场与回击电流波形之间的关系。

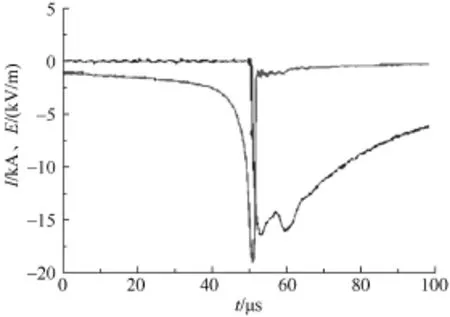
图1 雷电电磁场和回击电流的实测波形

1 近场空间LEMP表达式

在雷电垂直回击通道条件下，如图2所示，假设大地电导率无穷大，回击速度为v，回击通道长为H，i是回击电流，观测点水平距离为r、高度为z，Er、Ez、Hψ分别是水平电场、垂直电场以及角向磁场。

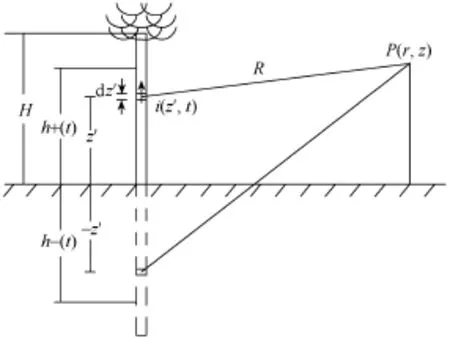
图2 雷电回击TL模型

图2 所示三维空间任一观测点P（r, z）位置的电磁场精确表达式为[10]

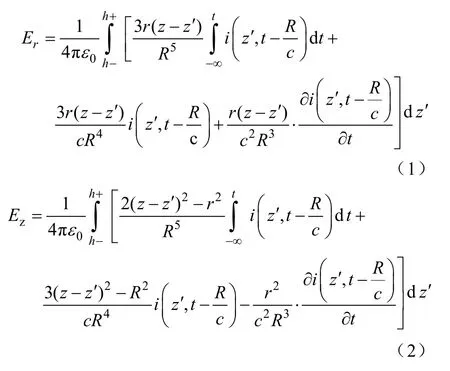
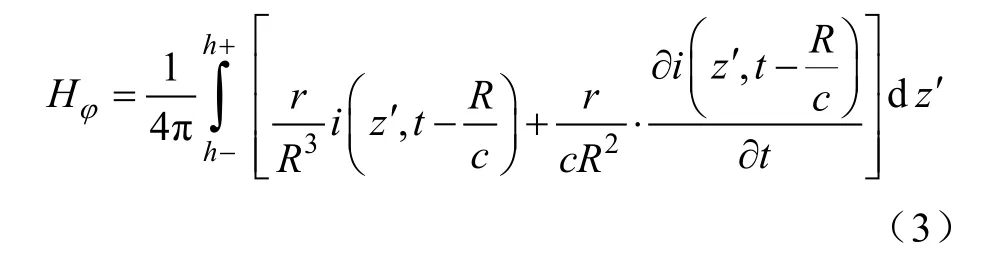
我们对近场区空间不同高度垂直电场进行了计算，结果如图3所示。从图3可知，在近场区空间不同高度垂直电场波形与z=0时地表波形存在明显区别，而由文献[13]知，地表垂直电场波形与底部电流波形相似。所以，z≠0时，近场区垂直电场波形与底部电流波形基本无近似关系，本文仅对水平电场和角向磁场展开分析研究。

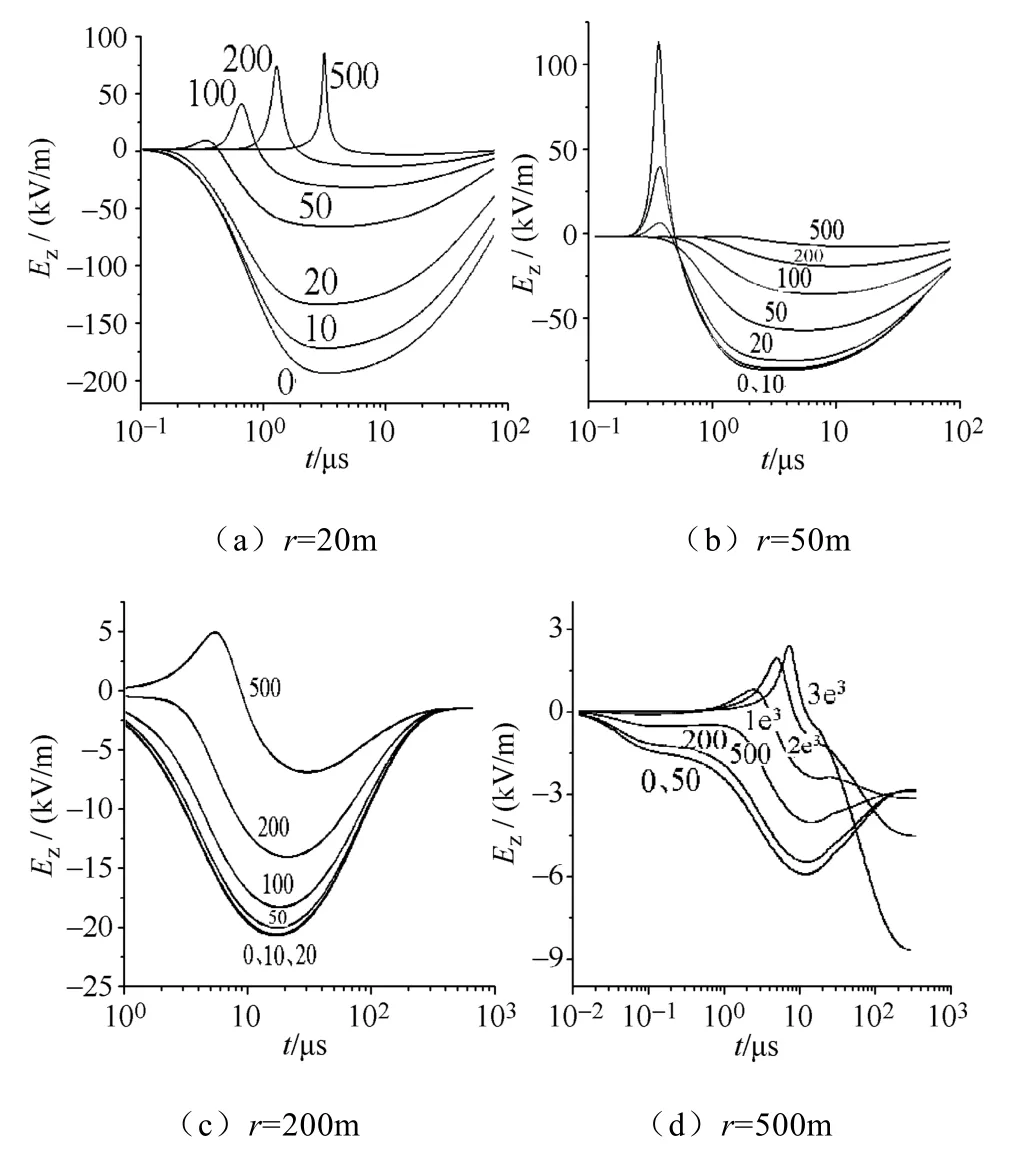
图3 近场区空间不同高度的垂直电场波形比较

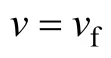
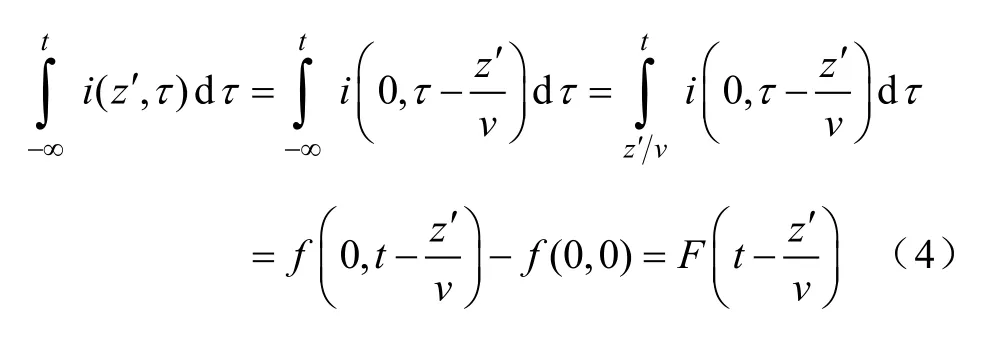
所以，式（1）中电流部分积分为

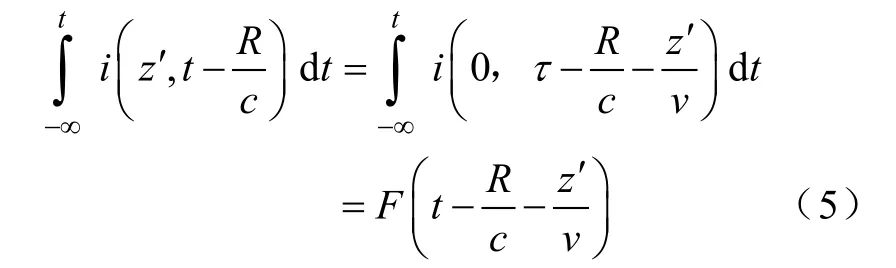
因此，忽略掉水平电场分量式（1）中的1/c2项，其一阶近似表达式为

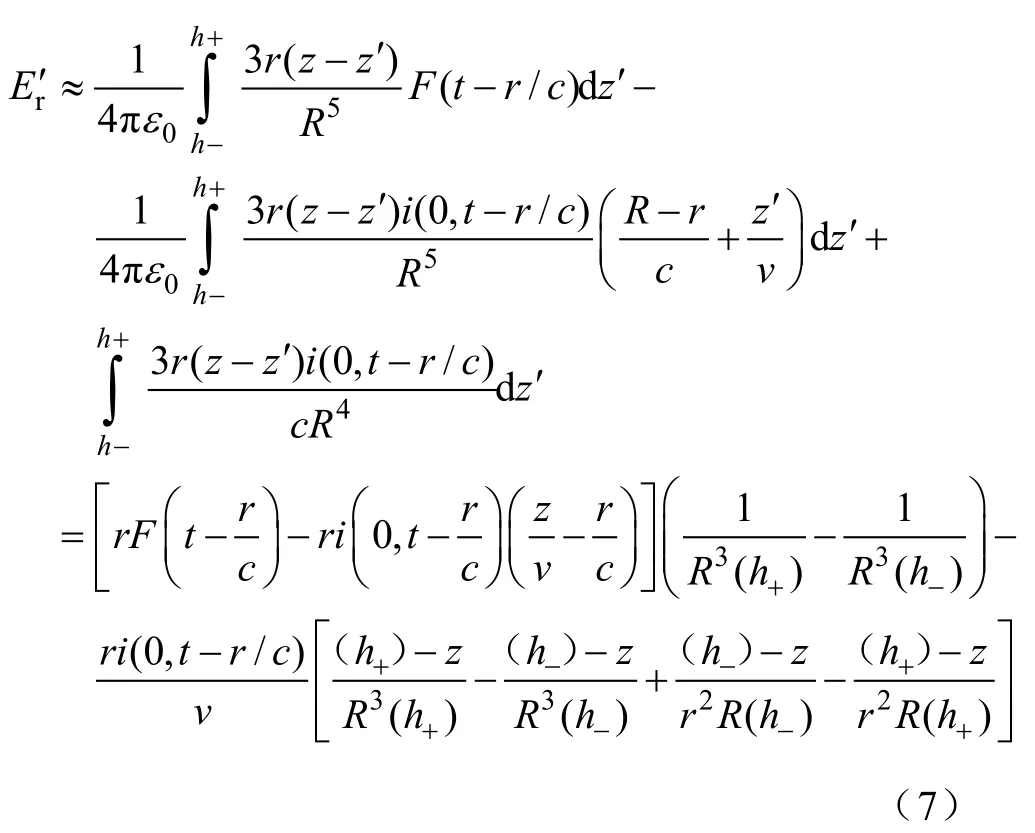
类似的，近场区角向磁场的一阶近似表达式为

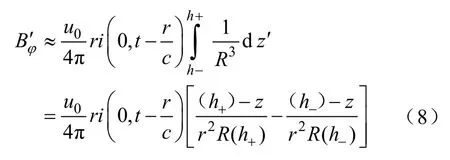
R在时间增大的过程中趋近于|h+|和|h-|，忽略一阶近似表达式（7）和式（8）中的1/R3项，进一步得到其二阶近似表达式，即

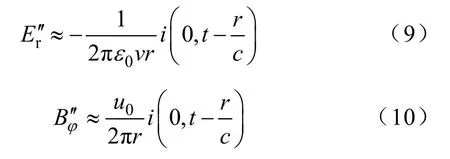
2 精确计算结果与近似结果的比较

观察式（9）和式（10）发现，近场区空间雷电电磁场的二阶近似表达式与通道底部电流的表达式只相差一个系数，能更直观的表达雷电电磁场波形和回击电流波形之间的关系，而一阶近似表达式只是在精确表达式基础上忽略了辐射场部分，属于精确表达式和二阶近似表达式的过渡式，因此，可以说近场区空间雷电电磁场波形与标度化的通道底部电流波形是近似一致的，只需比较精确波形和二阶近似波形即可反映雷电电磁场和回击电流的近似关系。为了进一步研究以上所得近场区电磁场近似公式的精确性，对精确解式（1）、式（3）和近似解式（7）至式（10）的电磁场波形进行了比较。计算过程中选取“8/20μs”雷电流波形，此时相关参数为[6]：I0=30kA，n=2，1τ=4×10-6s，2τ=6.25×10-6s，H=7.5km，v=1.3×108m/s。

图4至图7所示为近场区空间不同水平距离处不同高度的水平电场与其一阶、二阶近似波形的比较。从这些图中可以发现，随着观测点距回击通道的距离以及距地面高度的增加，水平电场精确波形与其近似波形之间的偏差呈现先减小后增大的趋势。在距回击通道50m以内、高度为几十米到几百米的空间内水平电场的精确波形与其两级近似波形基本重合，但当高度达到500m时，其一阶近似波形与精确波形就有了较大的区别。而距回击通道100m以外，在任意高度，水平电场与其近似波形均存在明显的区别。

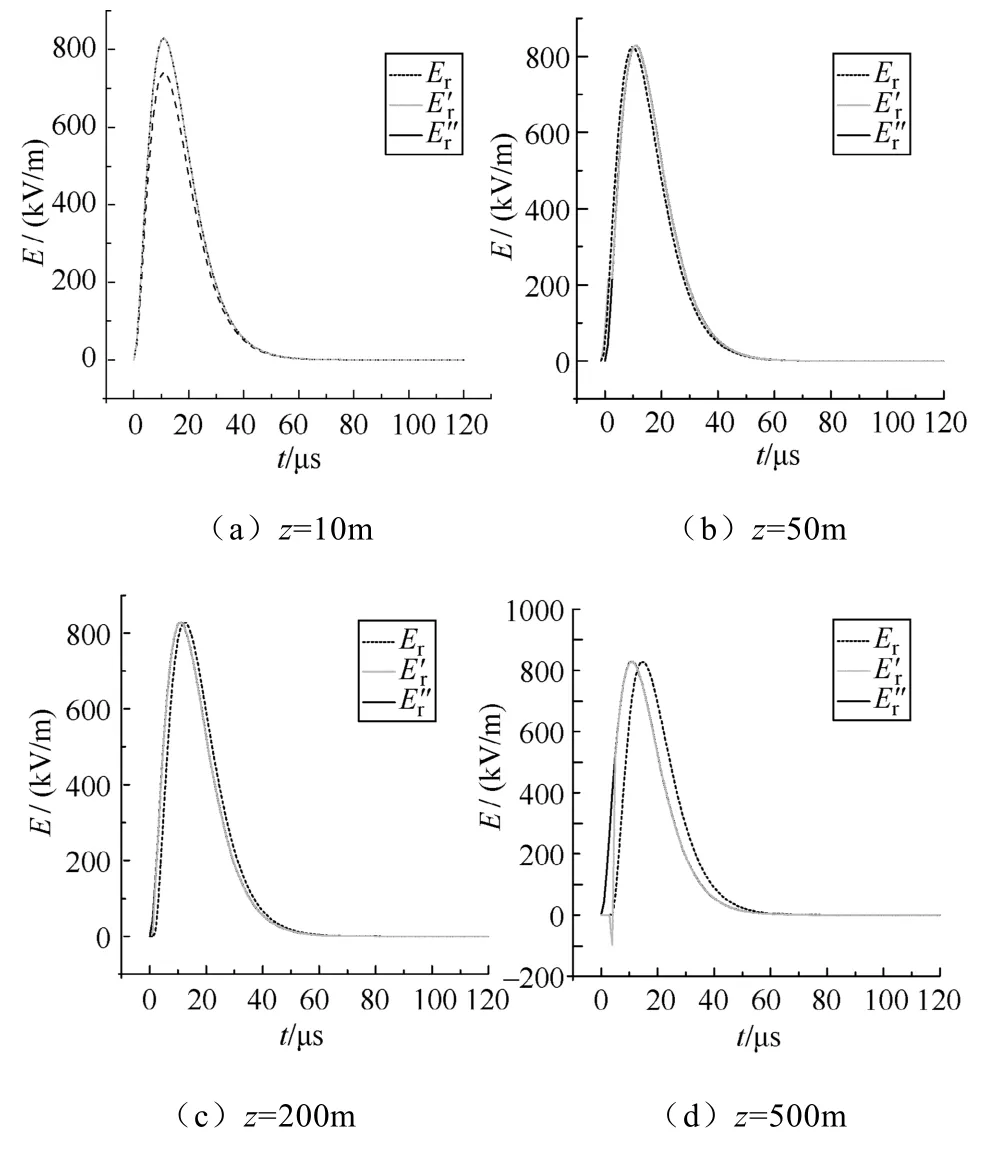
图4 r=5m处不同高度水平电场与其两级近似波形比较

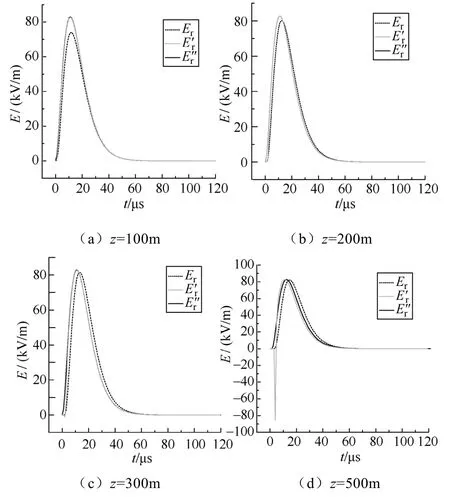
图5 r=50m处不同高度水平电场与其两级近似波形比较

图6 r=100m处不同高度水平电场与其两级近似波形比较

图7 r=500m处不同高度水平电场及其两级近似波形比较

图8 r=5m处不同高度的磁场与其两级近似波形比较

图8 至图11所示为不同水平距离处不同高度的磁场与其一阶、二阶近似波形的比较。从这些图中可以发现，随着观测点距回击通道的距离以及距地面高度的增加，角向磁场精确波形与其近似波形之间的偏差也逐渐增大。对比水平电场与角向磁场可知，在近场区空间角向磁场精确波形与其近似波形与水平电场相比，具有更高的重合性。在距离回击通道200m以内、离地高度500m以下的空间内角向磁场的精确波形与其两级近似波形基本重合；而在距离回击通道200m以外或高度500m以上的区域内，磁场与其近似波形存在明显的区别。

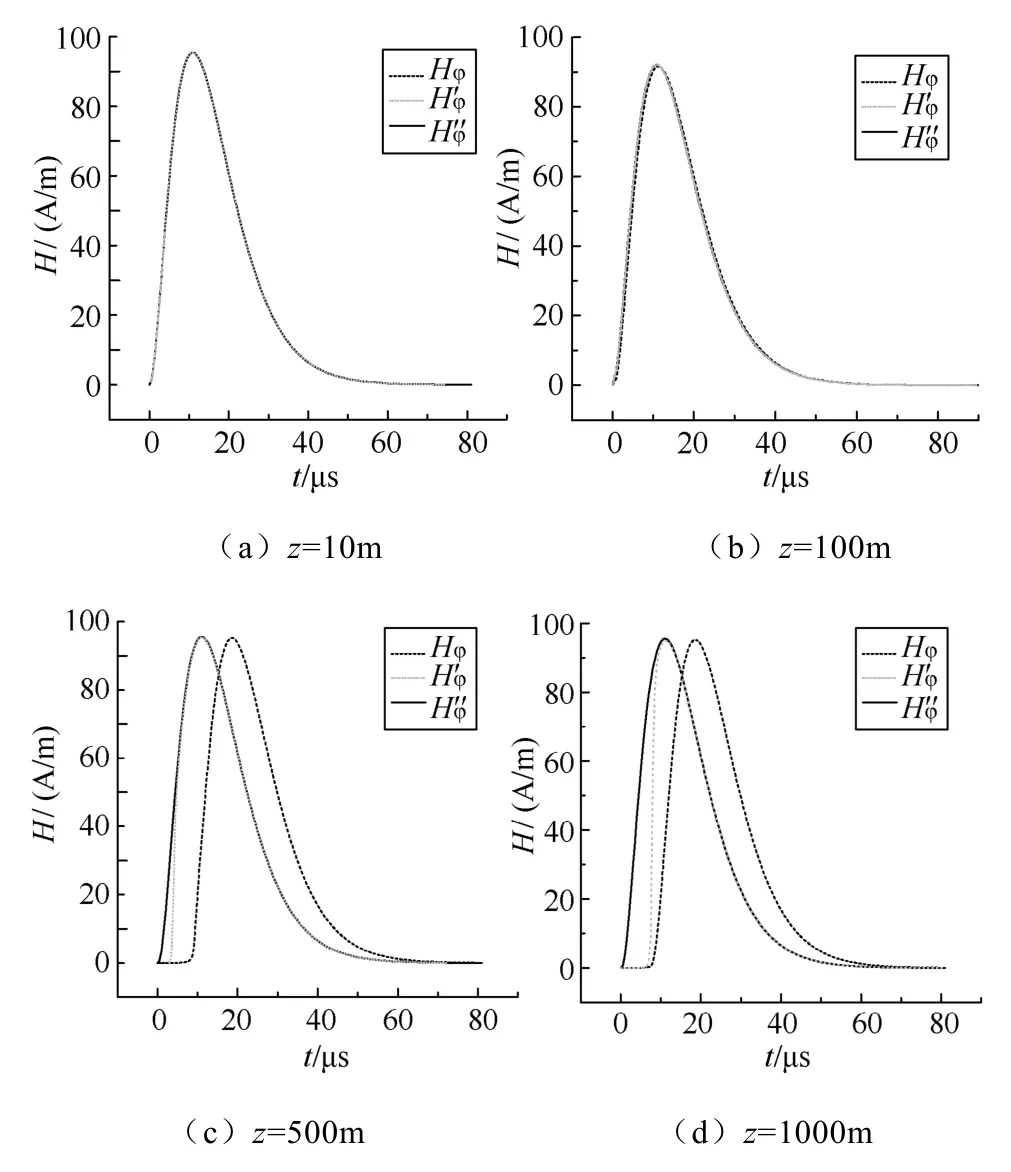
图9 r=50m处不同高度的磁场与其两级近似波形比较

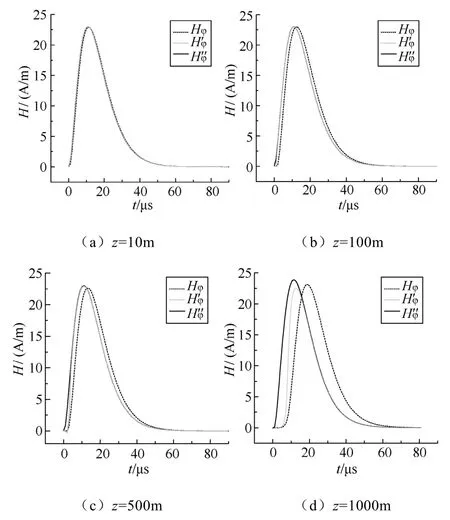
图10 r=200m处不同高度的磁场与其两级近似波形比较

图11 r=500m处不同高度的磁场与其两级近似波形比较

出现上述现象的原因是，在推导电磁场的两级近似表达式时作了一系列的近似处理，主要如下所述。

1）计算近场区空间静电场的一阶近似表达式时，忽略了水平电场分量式（1）中的1/c2项。

2）计算近场区空间感应场的一阶近似表达式时，用i(0,t-r/c)近似替换i(0,t-R/c-z′/v)。

3）计算近场区空间磁场的一阶近似表达式时，用i(0,t-r/c)近似替换i(0,t-R/c-z′/v)，并省略磁场的辐射场项。

4）R在时间增大的过程中趋近于h+和h-。

5）计算近场区空间电磁场的二阶近似表达式时，忽略了一阶近似表达式中的R-3项。

由于近场区空间电磁场两级近似公式是在假设r＜＜H的条件下推导的，随着距离r和z的增加，回击电流在回击通道中上升的越来越高，这一假设逐渐受到限制，使得省略的所有含r和z的项带来的误差越来越大，省略的电磁场辐射场分量越来越大且用i(0,t-r/c)近似替换i(0,t-R/c-z′/v)带来的误差也越来越大,因此，随着观测点距回击通道水平距离及距地面垂直高度的增加，LEMP的波形与标度化的回击通道底部电流波形之间的重合性越差。

3 结论

本文基于垂直回击通道模型推导了三维空间近场区任意高度LEMP的两级近似公式。通过改变观测点的位置，对电磁场的精确波形和两级近似波形进行对比，结果如下。

1）在近场区一定空间内水平电场和角向磁场分别与其两级近似波形近似，且它们之间的偏差随着观测点的位置距回击通道距离的增加而增大。

2）在距离回击通道50m以内、高度为几十米到几百米的空间内水平电场的精确波形与其两级近似波形基本重合。

3）在距离回击通道200m以内、离地高度500m以下的空间内角向磁场的精确波形与其两级近似波形基本重合。

4）在近场区同一空间区域内，磁场与其两级近似波形之间的偏差要比水平电场小，磁场波形与回击通道底部电流波形之间具有更高的近似性。

[1] 虞昊. 现代防雷技术基础[M]. 北京: 清华大学出版社, 2005.

[2] Rakov V A, Rachidi F. Overview of recent progress in lightning of recent progress inlightning research and lightning protection[J]. IEEE Transactions on Electromagnetic Compatibility, 2009, 51(3): 428-442.

[3] Hussein A M, Milewski M, Janischewskyj W. Correlating the characteristics of the CN Tower lightning return-stroke current with those of its generated electromagnetic pulse[J]. IEEE Transactions on Electromagnetic Compatibility, 2008, 50(3, 2): 642-650.

[4] 张岩, 刘福贵, 汪友华, 等. 改进的双指数函数雷电流波形及其辐射电磁场的计算[J]. 电工技术学报, 2013, 28(S2): 133-139.

[5] 樊亚东, 于建立, 詹清华, 等. 基于多阶FDTD雷电感应过电压计算新方法[J]. 电工技术学报, 2015, 30(12): 336-343.

[6] 熊小伏, 方伟阳, 程韧俐, 等. 基于实时雷击信息的输电线强送决策方法[J]. 电力系统保护与控制, 2013, 41(19): 7-11.

[7] 李涵, 邓雨荣, 朱时阳, 等. 海-陆混合路径对雷电电磁场传播的影响[J]. 电工技术学报, 2014, 29(1): 229-235.

[8] 牛萍, 田德宝, 蒋焕宇, 等. 雷击风险评估在防雷设计中的作用分析[J]. 电气技术, 2016(2): 83-87.

[9] Uman M A, Mclain D K. Kride E P. The electromagnetic radiation from a finite antenna[J]. Amer J Phys, 1975, 43: 33-38.

[10] 陈亚洲. 雷电电磁脉冲场理论计算及对电引信的辐照效应实验[D]. 石家庄: 军械工程学院, 2002.

[11] 王琳, 陈亚洲, 杜思尚, 等. 地表近区雷电回击电磁场的计算与特征分析[J]. 高电压技术, 2012, 38(11): 2899-2905.

[12] 陈亚洲, 肖雪荣. 地表近场LEMP与回击电流的近似性[J]. 高电压技术, 2007, 33(12): 23-26.

[13] 王晓嘉, 陈亚洲, 李冰, 等. 基于斜向通道模型的雷电电磁场近场近似特性[J]. 高电压技术, 2013, 39(3): 648-654.

[14] Leteinturier C, Weidman C, Hamelin J. Current and electric field derivatives in triggered lightning return strokes,J. Geophys. Res., 95, 1990: 811-828.

[15] 樊灵孟, 何宏明, 钟定珠, 等. 人工引雷试验中雷电流测量分析[J]. 高电压技术, 2000, 26(4): 50.

[16] 郄秀书, 杨静, 蒋如斌, 等. 山东人工引发雷电综合观测实验及回击电流特征[J]. 大气科学, 2012, 36(1): 77-88.

Study on Spatial LEMP Waveform Characteristics in Near-Field

Wang Lipeng Chen Yazhou Wan Haojiang Wang Xiaojia
(Institute of Electrostatic and Electromagnetic Protection, Ordnance Engineering College, Shijiazhuang 050003)

In order to have a further study on spatial LEMP waveform characteristics, the LEMP and the lightning return stroke channel base current were theoretically researched. According to the TL model, it was derived that the relations of spatial LEMP and return stroke channel base current in the near-field. Compared the calculated waveforms of the exact expressions and approximate expressions, and it was found that within a horizontal distance no more 50m from return stroke channel and a vertical height that was from tens meters to hundreds meters, the vertical electric field and its approximate waveforms were basically superposed. Within a horizontal distance no more 200m from return stroke channel and a vertical height no more 500m from ground, the magnetic field and its approximate waveforms were essentially coincident.

LEMP; lightning return stroke channel base current; near-field; exact waveforms; approximate waveforms

王李鹏（1991-），男，山西省晋城市人，硕士生，研究方向为电磁兼容与防护技术。