均质腔内壁微结构对均质性能影响的仿真分析
2017-04-12史岩彬荣学青
董 树 史岩彬 荣学青
(齐鲁工业大学机械与汽车工程学院,山东 济南 250353)
均质腔内壁微结构对均质性能影响的仿真分析
董 树 史岩彬 荣学青
(齐鲁工业大学机械与汽车工程学院,山东 济南 250353)
基于壁面粗糙度引起流动状态变化的现象,为进一步研究高压均质机内均质腔内壁表面的微结构对均质性能的影响,在光滑均质腔内壁构建沟槽状微结构,采用计算机流体动力学(CFD)技术对均质腔内两相流动过程进行仿真。以APV实验型高压均质机内的均质腔为研究对象,将油-水乳液作为均质物料,分别对光滑均质腔,矩形截面沟槽均质腔,以及三角形截面沟槽均质腔内的均质过程进行仿真计算,并做对比分析。结果表明:有沟槽的均质腔均质粒径更小,而矩形截面沟槽较三角形截面沟槽均质得到的粒径更小,同时粒度分布更均匀,有利于提高均质性能;计算机仿真结果与湍流近壁区理论分析结果趋势一致。
均质腔;湍流近壁区理论;内壁微结构;流体动力学
高压均质机是液体物料均质细化和高压输送的专用设备和关键设备,其主要原理是使物料在通过均质阀时,在高压下产生强烈的剪切、撞击、空穴和湍流蜗旋作用,使液态物料或以液体为载体的固体颗粒得到超微细化。高压均质机均质产品质量的影响主要有:① 提高产品的均匀度和稳定性;② 增加保质期;③ 减少反应时间从而节省大量催化剂或添加剂;④ 改变产品的稠度、口味和色泽等等。
高压均质机近年来的发展主要表现在工作压力的提高和均质阀结构(或均质腔)的变化上,其中均质阀作为均质机的核心结构被不断研究和发展。均质阀(或均质腔)的结构变化反映了均质方式的差异和均质效果[1-3]。均质阀内的工作空腔称作均质腔。根据湍流近壁区的理论[4]分析,均质腔壁的粗糙度增加,壁面的表面摩擦系数Cf也随着增加,湍流在近壁区的一些动力参数也发生改变。
在以往对均质腔的研究中,对狭缝区域的分析比较多,因为流体在狭缝处能量交换集中,物料主要在狭缝处发生均质细化。通过分析,流体在均质腔壁处也会有能量变化,如:湍动能减小,并且壁面的粗糙度越大湍动能减小的幅度越大。均质腔壁表面的微结构增加了壁面的粗糙度。为了探究腔壁表面的微结构对均质性能的影响,本试验对油-水乳液在高压均质腔内的流动过程进行数学建模和数值计算,得到速度、湍流耗散率、均质粒径等结果。
1 油滴在均质腔内的流动分析
1.1 粗糙壁面对湍流的影响
粗糙元主要作用是产生形状阻力,并反馈给流体[5]。由于粗糙元的存在,粗糙壁面的一些物理参数比光滑壁面的大。如粗糙壁面的平均剪切应力要比光滑壁面的大,并且随着粗糙度的增大,平均剪切应力增大;随着粗糙度的增加,粗糙壁面的法向脉动速度不断增大,从而导致粗糙壁面上湍流耗散率ε增加[6-8]。根据文献[7]中的结论,制做了一个简单的管道模型,用于分析管道壁的粗糙度对湍流的影响,结果见图1。

图1 流道内的剪切力和湍流耗散率Figure 1 Shear stress and turbulent dissipation rate in the flow channel
由图1可知,对于同一模型,湍流在流道内的剪切力和湍流耗散率随壁面粗糙度的增加而增大。这是因为粗糙元的存在使粗糙微流道内的流场不同于光滑流道,特别是在壁面附近区域,在粗糙元背面的角落区域形成旋涡状回流区[9]。
1.2 油滴破碎的理论分析
均质腔内瞬间失压的流体以极高的流速喷出,碰撞在均质阀组件之一的冲击环上,产生3种效应:空穴效应、撞击效应、剪切效应。其中剪切效应是高速流体通过均质腔通道和缝隙时产生的强烈剪切作用。
基于剪切效应,油滴破碎主要是由垂直于油滴表面的惯性力作用[10]。当颗粒雷诺数大于1时,惯性力以流体粘滞力为主,这种流体黏滞力对油滴产生了剪切作用。其中颗粒雷诺数Red公式为[11]:
(1)
式中:
Red——颗粒雷诺数;
ρC——连续相密度,kg/m3;
d——粒径,m;
μC——连续相黏度,kg/m。
在油-水乳液中,连续相是水,水相密度为1 000 kg/m3,水相黏度约为0.001 kg/m,初乳中油滴的粒径范围1~100 μm,且vdx-vx>>1 m/s。根据文献[11]油滴所受剪切力大小由FDR决定。
其中FDR公式为[11]:
(2)
式中:
FDR——单位质量油滴的拖拽力,N/kg;
ρD——离散相密度,kg/m3;
CDR——曳力系数。
将方程(1)带入到方程(2)中,得
(3)
在方程(3)中,水相密度ρC,离散相油相密度ρD,和初乳中油滴直径d是不随壁面粗糙度变化的量。当Red>500时,曳力系数CDR为常数0.44;当1 (4) 方程(3)转变为 (5) 水相黏度μC也是不随壁面粗糙度变化的量。经过分析油相和水相的速度差vdx-vx随壁面粗糙度增大而增大,即FDR随壁面粗糙度增大而增大。所以油滴在流道内受到的剪切力随壁面的粗糙度增大而增大。 油-水乳液在均质腔内能够被湍流破碎的油滴的最小粒径由方程(6)来确定, (6) 式中: dmin——被湍流破碎的最小粒径,m; εE——乳液的湍流耗散率,m2/s3; ρE——乳液密度,kg/m3。 由方程(6)可知,在均质腔内湍流耗散率越大,油滴越容易发生破碎。根据图1(b)可知,湍流耗散率随壁面的粗糙度增大而增大,所以dmin随壁面的粗糙度增大而减小,即在壁面粗糙的均质腔内获得较小的油滴直径。 以APV实验型高压均质机为研究对象,将油-水乳液作为均质物料建模。根据1.1中对粗糙壁面湍流边界层的分析,在均质腔壁上分别构建矩形截面沟槽和三角形截面沟槽微结构增加壁面粗糙度。其中高压均质腔的结构见图2。 1. 入口 2. 出口 3. 阀杆 4. 冲击环 5. 均质阀底座 6. 狭缝 7. 均质腔 8. 均质腔外固体结构 9. 均质腔壁 10. 矩形沟槽 11. 三角形沟槽 图2 均质腔结构图和沟槽放大图 Figure 2 Homogeneous cavity structure and groove larger image 在用CFD计算时,粘性模型选用标准k-ε双方程模型,多相流模型选用DPM模型[12-13]。设油-水乳液进入均质腔的压力为40 MPa,乳液中油的体积分数为10%。所以CFD计算时的条件设置参数见表1。 初始化并迭代,计算完成后分析均质腔内湍流耗散率的变化和均质后的粒径分布。 3.1 速度云图 迭代计算完成后的速度云图见图3(a),均质腔内速度最大值出现在狭缝处,且速度分布见图3(b)。通过Surface Integrals计算出3种均质腔内的最大速度见表2。通过比较,3种均质腔内的最大速度变化不大。 均质腔壁处的速度比较小,在速度云图中变化不明显,通过Surface Integrals计算出腔壁处的平均速度值见表2。通过比较,由于均质腔壁细微的结构变化,导致3种均质腔壁处的平均速度不同,其中光滑壁面均质腔的平均速度最大,三角形沟槽均质腔次之,矩形沟槽均质腔最小。 表1 仿真条件设置参数Table 1 Simulation parameters 图3 速度分布图Figure 3 Velocity distribution 3.2 湍流耗散率 均质腔[图2(b)]上的湍流耗散率见图4,其中图4(a)、(b)、(c)分别是光滑均质腔、矩形沟槽均质腔和三角形沟槽均质腔的湍流耗散率。 由图4可以看出,3种结构的均质腔湍流耗散率的最大值都是出现在狭缝处。由表2可以看出,加入沟槽结构后,均质腔内湍流耗散率的最大值比光滑均质腔的大了2个数量级,并且矩形沟槽均质腔比三角形沟槽均质腔稍大。由于沟槽结构的不同,在均质阀底座处的流道内的湍流耗散率不同。由表2可以看出,矩形沟槽均质腔均质阀底座处流道内平均湍流耗散率比三角形沟槽均质腔内的稍大,比光滑均质腔大了3个数量级。由文献[9]可知,这是因为沟槽增加了腔壁的流阻并且在沟槽内产生了回流区,其中矩形沟槽在流道内产生的流阻和回流区最大。 表2 3种均质腔的计算结果Table 2 Calculation results of three homogeneous cavities 图4 湍流耗散率分布图Figure 4 Turbulent dissipation rate distribution 3.3 粒径分布 3种均质腔均质后输出的油滴直径分布见图5。 由图5可以看出,3种结构的高压均质腔中,设计沟槽的均质腔与光滑均质腔相比均质后的油滴直径减小。其中矩形沟槽均质腔均质粒径比三角形沟槽均质腔的均质粒径更小。这个结果和1.2中分析得出的结论一致,即均质腔内湍流耗散率越大,均质后输出的粒径越小。由图5还可以看出,矩形沟槽均质腔比三角形沟槽均质腔和光滑均质腔均质得到的粒径分布更均匀。 图5 模拟输出的油滴直径Figure 5 Output oil drop diameter of simulation (1) 本试验研究了高压均质腔内,腔壁表面微结构对均质腔内流体流动状态以及均质性能的影响。均质腔壁上设计沟槽状微结构,增加了腔壁的表面粗糙度。在有流体流经均质腔时,与光滑均质腔相比,流体在有沟槽的均质腔内受到的壁面剪切力大。 (2) 高压均质腔内的湍流耗散率最大值,矩形沟槽的均质腔比三角形沟槽均质腔的稍大,比光滑均质腔的大2个数量级,并且都出现在狭缝处。均质阀底座处的流道内的平均湍流耗散率,矩形沟槽的均质腔比三角形沟槽均质腔稍大,比光滑均质腔的大3个数量级。 (3) 高压均质腔均质后的粒径变化。设计沟槽后的均质腔均质粒径比光滑均质腔的均质粒径明显减小。并且矩形沟槽均质腔均质粒径比三角形沟槽均质腔均质粒径减小幅度更大。 (4) 在光滑均质腔内壁增加沟槽结构,能够减小均质粒径,粒度分布更均匀,提高了均质机的均质性能。并且沟槽的形状对均质机的均质性能也有一定的影响。本试验结果表明矩形沟槽比三角形沟槽效果更显著。 (5) 研究均质腔壁表面微结构对均质结果的影响,为均质阀的加工提供了新的思路,在加工均质阀阀座和碰撞环的内表面时增加其表面粗糙度。也为以后用特定的加工方法在均质腔内壁加工微织构,对均质腔进行优化改进提供了依据。 [1] 雒亚洲, 鲁永强, 王文磊. 高压均质机的原理及应用[J]. 中国乳品工业, 2007(10): 55-58. [2] 刘斌, 吴雪, 冯涛, 等. 均质阀结构分析[J]. 食品与机械, 2014, 30(1): 104-106. [3] LEV A R. Analysis and calculation of the efficiency of a homogenizing valve[J]. Journal of Food Engineering, 1994, 23(4): 429-448. [4] Fluent Inc. Fluent user’s guide[M/CD]. Lebanon: Fluent Inc, 2003: 47-53. [5] TGUNNAR J, FARAZ M, JONATHAN W N. Some Problems with Near-Wall Measurements and the Determination of Wall Shear Stress[J]. Journal of Innovation Economics, 2006, 2(2): 3-13. [6] 刘骁飞, 韦安阳, 罗坤, 等. 粗糙壁面上湍流边界层的直接数值模拟[J]. 工程热物理学报, 2014, 35(12): 2 425-2 428. [7] KIRAN B, JOHN K, GARY C. Effect of Roughness on Wall-Bounded Turbulence[J]. Flow Turbulence and Combustion, 2004,72: 463-492. [8] KROGSTAD P, ANTONIA R A. Structure of turbulent boundary layers on smooth and rough walls[J]. Fluid Mech, 1994, 277: 1-20. [9] 谭德坤, 刘莹. 壁面粗糙度效应对微流体流动特性的影响[J]. 中国机械工程, 2015, 26(9): 1 210-1 214. [10] PER J B, FRANCOIS P, AREND D, et al. Coupled population balance-CFD simulation of droplet breakup in a high pressure homogenizer[J]. Computers and Chemical Engineering, 2014, 68: 140-150. [11] PAOLO C, ANDREA V, GIAN L B. A numerical procedure for predicting the performance of high pressure homogenizing valves[J]. Simulation Modelling Practice and Theory, 2010, 18: 125-138. [12] AKIRA S, JUNZO S, TAKEO N, et al. Effect of back pressure on emulsification of lipid nanodispersions in a high-pressure homogenizer[J]. International Journal of Pharmaceutics, 2012, 422: 489-494. [13] ANDREAS H, LASZLO F, FREDRIK I, et al. Experimental validation ofk-RANS-CFD on a high-pressure homogenizer valve[J]. Chemical Engineering Science, 2012, 71: 264-273. Simulation analysis of the effecton homogeneous performance from micro structure of homogeneous cavity inner wall DONG ShuSHIYan-binRONGXue-qing (SchoolofMechanical&AutomotiveEngineering,QiluUniversityofTechnology,Jinan,Shandong250353,China) Based on the phenomenon that the change of flow state caused by the wall roughness, in order to research the effect of micro structure on the surface of the inner wall of the high pressure homogenization cavity in the high pressure homogenizer to homogenization performance, the groove micro structure is structured on the inner of smooth homogenization cavity, and a computer fluid dynamics (CFD) technique is used to model the two-phase flow in a high pressure homogenizer. This paper will study the high pressure homogenization cavity in the APV-high pressure homogenizer, the oil-water emulsion as the homogeneous materials, the smooth homogeneous cavity and the rectangular section groove homogeneous cavity and the triangular section groove homogeneous cavity are simulated and calculated respectively, and the results are compared. The results show that the homogeneous cavity with groove which has a smaller particle size than the smooth homogeneous cavity after homogenization, the rectangular section groove homogeneous cavity has a smaller particle size than the triangular section groove homogeneous cavity after homogenization, at the same time the particle size distribution is more uniform, improved the homogeneous performance. The results of computer simulation to the results trend obtained by the theoretical analysis of the turbulent near-wall region shows very good agreement. homogeneous cavity; the near -wall region of turbulent; micro structure of wall surface; fluid dynamics 国家自然科学基金(编号:21203112);山东省重点研发计划项目(编号:2015GGX103022) 董树,男,齐鲁工业大学在读硕士研究生。 史岩彬(1979—),男,齐鲁工业大学教授,博士。 E-mail:shiyanbin79@163.com 2016—12—02 10.13652/j.issn.1003-5788.2017.02.0162 油-水乳液均质过程的仿真建模
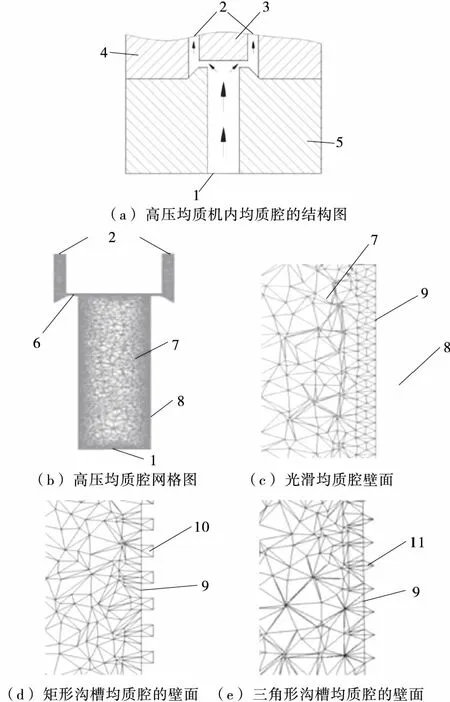
3 仿真结果与分析
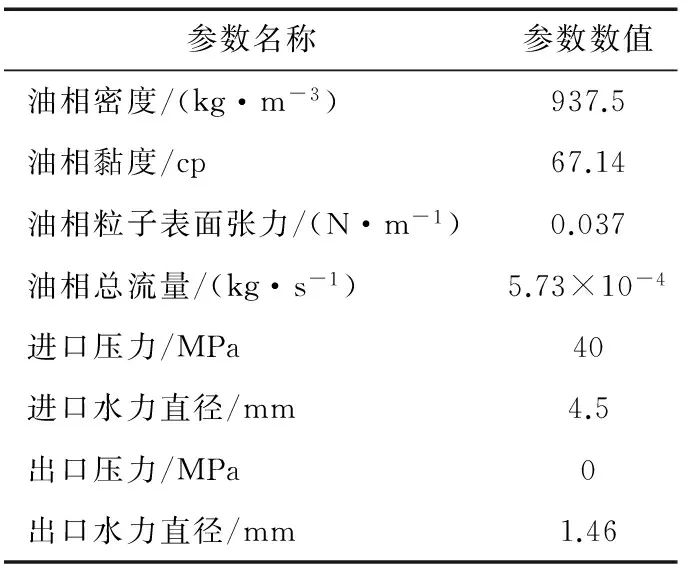
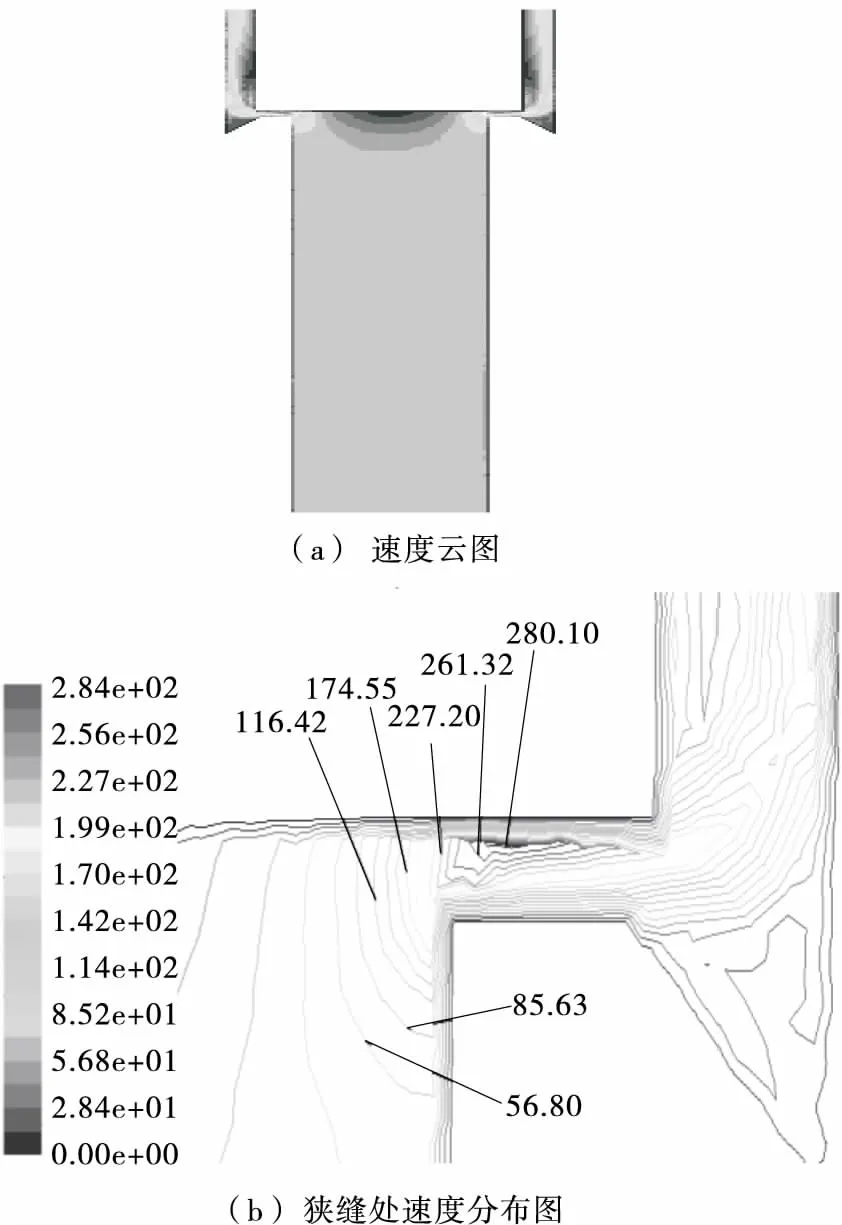

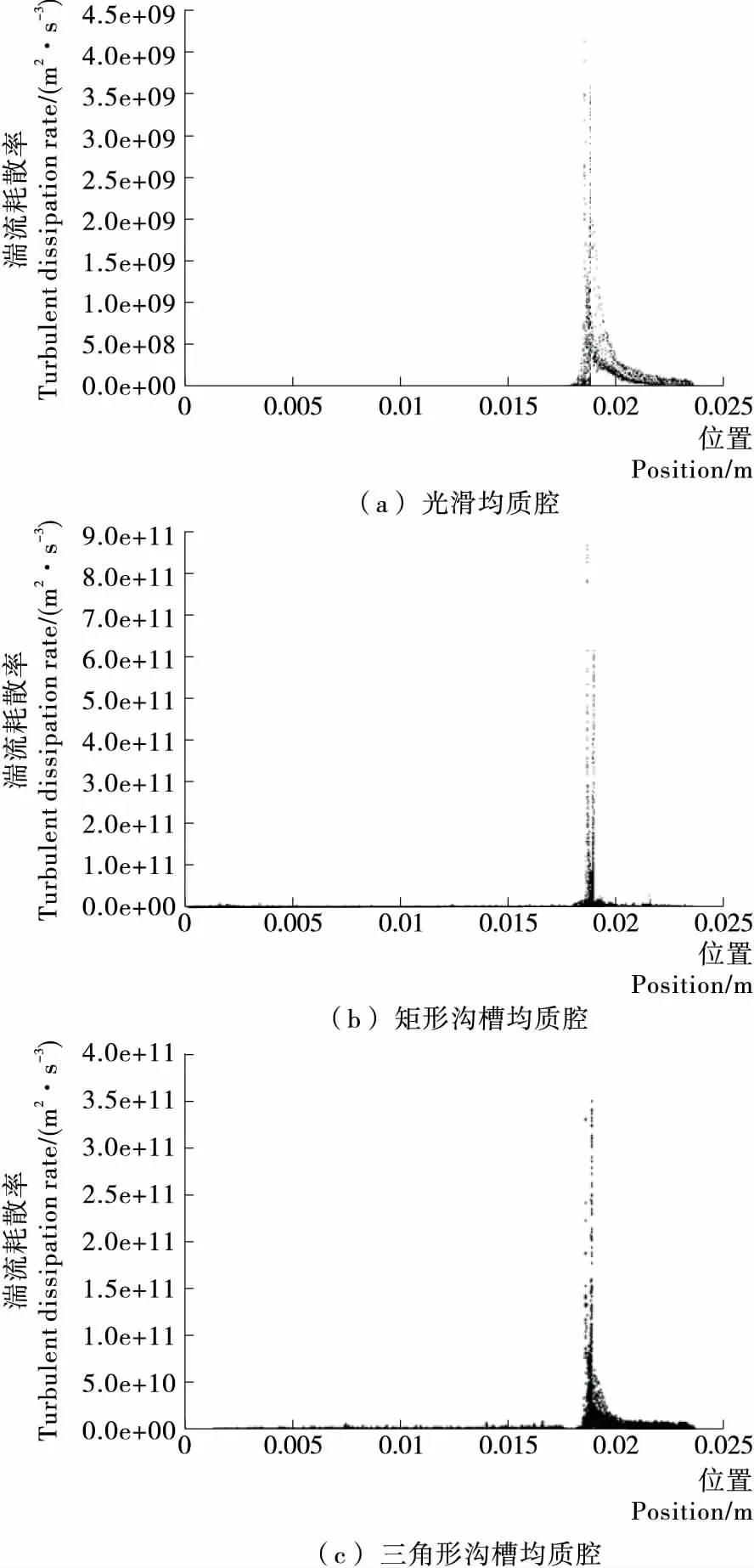

4 结论
