简支梁弹性临界弯矩计算方法研究进展
2017-04-12郭兵孙乃毅杨大彬
郭兵,孙乃毅,杨大彬
(1.山东建筑大学土木工程学院,山东济南250101;2.荣成市建筑工程质量造价监督管理站,山东荣成264300)
简支梁弹性临界弯矩计算方法研究进展
郭兵1,孙乃毅2,杨大彬1
(1.山东建筑大学土木工程学院,山东济南250101;2.荣成市建筑工程质量造价监督管理站,山东荣成264300)
整体稳定系数是计算刚结构受弯构件整体稳定的重要依据,而弹性临界弯矩是影响整体稳定系数的主要因素,因此弹性临界弯矩准确与否直接影响稳定计算结果。目前,简单条件下简支梁弹性临界弯矩的计算方法采用的是精确法,但适用范围有限;复杂条件下简支梁弹性临界弯矩的计算方法采用的是简化法,对于任意荷载和侧向支撑条件下的简支梁临界弯矩,只能借助等效弯矩系数来进行简化计算。文章阐述了简单条件下的精确法、复杂荷载下的精确法、复杂条件下的简化法等不同结构荷载条件下求解临界弯矩方法的研究进展,通过研究在荷载作用点位置、相邻梁段间的支持、整体稳定系数等影响因素,阐述了复杂条件下弹性临界弯矩计算的简化法存在的问题、影响及根源,对复杂条件下的简支梁弹性临界弯矩计算的能量法进行了展望。
简支梁;弹性临界弯矩;简化法;等效弯矩系数;总势能
0 引言
钢结构中的受弯构件有可能发生整体失稳,需要利用整体稳定系数φb来进行相应的稳定计算,而影响φb的主要因素是构件的弹性临界弯矩Mcr,因此Mcr准确与否直接影响稳定计算结果[1-6]。弹性稳定理论最早由欧拉提出,已经发展了二百年,但有些问题至今没有彻底解决,简支梁的Mcr计算方法就是其中之一。
均匀受弯简支梁的Mcr计算公式可以通过静力平衡法得到,属于解析解[7-10],并无争议。非均匀受弯简支梁的Mcr计算公式从理论上讲可以通过能量法得到[7-10],但由于学术界对受弯构件的总势能公式及变形函数等问题还有不同的看法,导致Mcr的计算公式很多,利用不同公式得到的计算结果也存在一定程度的偏差。
采用能量法计算Mcr时要用到受弯构件的总势能公式,但目前总势能公式有很多种,比较有代表性的是Bleich公式[7]、吕烈武公式[8]和童根树公式[11]。对于双轴对称截面受弯构件,因截面不对称系数βy=0,上述3个总势能公式没有差别[9],所得Mcr公式亦相同,但当截面单轴对称时,βy≠0,3个总势能公式并不相同,所得Mcr公式[11]或者相关参数[12]也不相同。另外,利用能量法计算Mcr时需要先假设构件的侧向弯曲变形函数、扭转变形函数,所得Mcr属于近似解,Mcr的精度与假设变形函数的精度直接相关。
1956年,Salvadori[13]针对端弯矩作用下工字形截面简支梁的Mcr计算提出了一种简化方法,通过等效弯矩系数βb将非均匀受弯构件等效成均匀受弯,并给出了βb计算公式,该方法简便实用且精度较高,为复杂条件下简支梁的Mcr计算提供了一条思路。考虑到工程中的受弯构件大多承担横向荷载,1979年Kirby等[14]将上述简化方法推广至任意荷载形式下的双轴对称工字型截面简支梁,并给出了相应的βb计算公式,该公式仅适用于横向荷载作用点位于构件的截面剪心[15]。上述诸简化方法被美、英、日、加等很多国家和地区的规范采纳,我国规范也不例外。
后来,Greiner等[16]、Suryoatmono等[17]、Serna等[18]和陈骥[19]等又对Kirby提出的βb计算公式进行了修正,但区别不大,仍仅适用于横向荷载作用的截面剪心。罗金辉等[20]针对横向均布荷载及反对称弯矩共同作用下的单轴对称截面简支梁,杨波[21]针对一端弯矩和上翼缘横向均布荷载共同作用下的双轴对称截面简支梁,周芬等[22]针对上翼缘均布荷载、下翼缘跨中集中荷载共同作用下的双轴对称截面简支梁分别提出了相应的βb计算公式,可见βb的计算公式都有特定的适用范围。
周绪红等[23]曾给出过简支梁的Mcr通用计算公式,可适用于不同的荷载形式,比如端弯矩、满跨均布荷载、单个集中荷载,但只能为单一荷载,不适用于多种荷载同时作用。刘占科等[24]对周绪红的Mcr通用公式进行了修正,可同时考虑多种荷载,但更适合对称荷载,荷载越不对称偏差越大,当荷载反对称时完全不适用。管海龙等[25]也提出了Mcr的通用计算公式,可适用于端弯矩、均布荷载及集中荷载共同作用下的简支梁,荷载可以不对称,但其中的集中荷载数量只能为单个,而且均布荷载与集中荷载在截面上的作用点位置必须相同。褚昊等[26]针对单个移动集中荷载下的简支梁,给出了Mcr的表达式。
仅荷载形式就已经使简支梁的稳定问题非常复杂,当简支梁跨中设有任意侧向支撑时,相邻梁段间的支持作用将使问题变得更加复杂,目前各国规范普遍忽略了相邻梁段间的支持作用,计算结果很保守[15,27-29]。
由此可见,现有简支梁的弹性稳定理论还不完善,Mcr计算方法都有特定的适用范围,有些方法还过于简化,不能满足工程需求。虽然利用有限元等数值方法可以得到任意受弯构件的Mcr高精度值,但费时费力,对工程设计来说也不现实。为便于说明问题,文章针对双轴对称工字形截面弹性简支梁的现有各种Mcr计算方法进行讨论,通过若干典型算例,就其存在的问题以及产生问题的原因进行探讨,目的是找出今后的研究方向,以期引起学术界和工程界的重视。
1 简单条件下Mcr计算的精确法
当简支梁的荷载及边界条件都比较简单时,利用静力平衡法或者能量法可以得到弹性临界弯矩Mcr的解析解或者高精度解[7-10]。
1.1 均匀受弯简支梁
对于承担均匀弯矩M且跨中无侧向支撑的弹性简支梁,如图1所示,构件有可能发生侧向弯扭失稳,由静力平衡法得到的Mcr解析解可采用式(1)表示为

式中:Mcr为梁的弹性临界弯矩,N·m;l为梁的跨度,m;βy为截面不对称系数,无量纲;Iy为绕弱轴的惯性矩,m4;It为抗扭惯性矩,m4;Iω为翘曲惯性矩,m6;E为钢材的弹性模量,N/m2;G为钢材的剪切模量,N/m2。
1.2 跨中央单个横向集中荷载作用下的简支梁
当简支梁跨中央作用有单个横向集中荷载Q且跨中设有等间距布置的侧向支撑时,如图2所示,由能量法得到的Mcr高精度近似解可由式(2)表示为
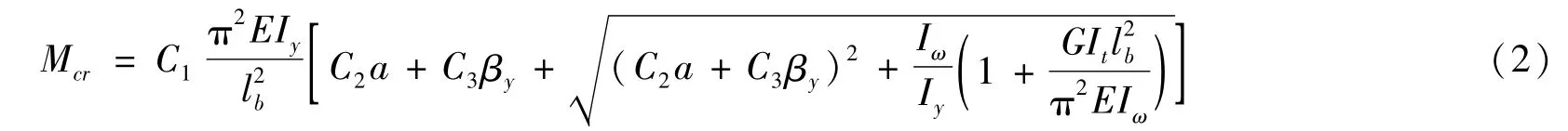
式中:C1、C2、C3分别为与侧向支撑数量有关的参数,无量纲,取值见表1,表中括号内为GB 50017—2012钢结构设计规范修订报批稿[30](规范修订报批稿)的建议值;lb为等间距布置的侧向支撑间距,m,如图2所示,当跨中无侧向支撑时lb=l;a为横向荷载作用点至截面剪心S的距离,m,当作用点位于剪心之上时a取负值,反之a取正值。
1.3 满跨均布荷载作用下的简支梁
当简支梁承担满跨均布荷载q且跨中设有等间距布置的侧向支撑时,采用能量法同样可以得到Mcr表达式,与式(2)完全相同,只有参数C1、C2、C3的取值不同,见表1。
由式(2)和表1可以看出,横向荷载类型、荷载作用点位置、侧向支撑数量等参数均对Mcr影响较大。由于式(2)是基于整个构件的总势能公式得出的,综合考虑了各种因素的影响,无需再进行修正。

图1 跨中无侧向支撑的均匀受弯简支梁图
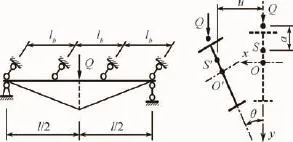
图2 跨中央单个横向集中荷载作用下的简支梁图

表1 参数C1、C2、C3值
1.4 端弯矩作用下的简支梁
当简支梁承担端弯矩M1、M2且跨中无侧向支撑时,利用能量法可得到Mcr的高精度近似解,因表达式较为复杂,可由式(3)[8-10]表示为

式中:βb为等效弯矩系数,无量纲;M0cr为均匀受弯简支梁的临界弯矩,由式(2)计算。
由式(3)可以看出,利用βb可以将非均匀受弯简支梁等效成均匀受弯简支梁,使稳定计算大为简化。影响βb的主要因素是荷载形式(端弯矩的比值)和梁截面类型,βb与M2/M1的关系曲线如图3所示,在阴影区范围内上下波动。1956年,Salvadori[13]通过分析后给出了两个βb的拟合公式,由式(4)和(5)表示为

式中:M1、M2为端弯矩,N·m。当|M1|≥|M2|,M1、M2使梁产生同向曲率时同号,而产生异向曲率时异号。

图3 端弯矩作用下简支梁的βb—M2/M1曲线图
欧洲EC 3—2005规范采纳了式(4)做为βb的上限;日本AIJ2010规范、加拿大CAN/CSAS16—09规范以及规范修订报批稿等多国规范采纳式(5)做为βb的下限。
2 复杂荷载下Mcr计算的精确法
对于跨中无侧向支撑的简支梁,当荷载比较复杂时也可以利用能量法得到弹性临界弯矩Mcr的高精度解[23-26],Mcr的表达式与Clark[31]给出的简单荷载下的Mcr表达式在形式上完全相同,由式(6)表示为
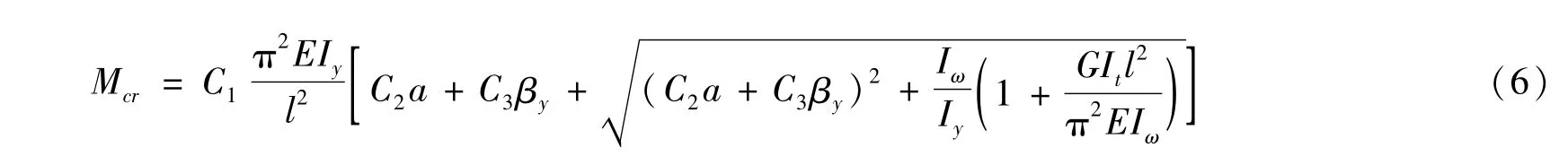
式(6)称为各类荷载下Mcr的通用表达式,不同的荷载形式对应不同的C1、C2、C3值,其中简单荷载下的C1、C2、C3值见表1。周绪红等[23]、刘占科等[24]、管海龙等[25]和褚昊等[26]都曾经给出过复杂荷载下C1、C2、C3的计算表达式,这些研究成果有以下共同的特点:
(1)C1、C2、C3需要进行复杂的积分运算,设计时不方便使用;
(2)具有一定的适用范围,要么要求荷载必须对称,要么对荷载数量有限制,在适用范围内是准确的,一旦超出范围,偏差很大。
因此,真正意义上的Mcr通用表达式并没有找到,但上述文献都为今后的研究提供了有益借鉴思路。目前各国规范对复杂条件下简支梁的Mcr只能采用简化方法来计算。
3 复杂条件下Mcr计算的简化法
虽然式(1)~(3)的精度较高,但有特定的适用范围,远不能满足工程中荷载形式、侧向支撑复杂多变的需求;式(2)虽然涉及到侧向支撑,但必须为等间距布置;式(6)虽然可以用于复杂荷载,但计算过程非常繁琐。因此目前各国规范中复杂条件下简支梁的弹性临界弯矩Mcr都是采用简化法来计算,也就是通过修改等效弯矩系数βb并借助于式(3)来进行计算。
复杂条件下简支梁可以分为两类:(1)荷载复杂,包括荷载形式、荷载在截面的位置等;(2)侧向支撑复杂,包括支撑的数量、位置等。
3.1 任意荷载作用下的简支梁
Kirby等[14]认为跨中无侧向支撑简支梁在任意荷载作用下的Mcr仍可用式(3)来计算,并给出了荷载作用在截面剪心时双轴对称工字形截面简支梁的βb经验公式,由式(7)表示为

式中:Mmax为梁的最大弯矩,N·m;MA、MB、MC分别为梁跨四分点处的弯矩(如图4所示),N·m;以上各弯矩均取绝对值。

图4 任意荷载作用下的简支梁图
对于荷载作用在截面剪心的双轴对称工字形截面简支梁,式(7)精度较高,被多国规范略加修改后推广至单轴对称工字形截面受弯构件,其中,规范修订报批稿及美国ANSI/AISC 360—10规范均采用式(8)表示为

英国BS5950—1:2000规范则采用了式(9)表示为

后来,Greiner等[16]采用有限单元法、Suryoatmono等[17]采用有限差分法分别研究了各类边界条件下荷载作用在剪心时双轴对称工字形截面受弯构件的βb,并提供了相应的计算表格。Serna等[18]利用上述成果,给出了双轴对称工字形截面的βb闭合解,由式(10)表示为
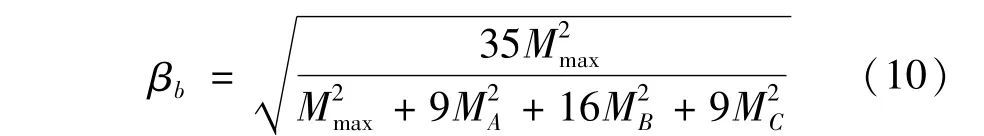
陈骥[19]认为式(10)的安全余地偏小,建议调整式(10)由式(11)表达为

以图5所示的两个双轴对称工字形截面简支梁为例,假设横向集中荷载Q均作用在构件的截面剪心,利用式(7)~(11)得到的βb值见表2,其中括号内为与有限元解的误差百分比。可以看出,最大误差不足6%,且均为负偏差,说明上述各式的精度较高且略偏安全。
虽然图5(b)所示简支梁的跨中央设有一个侧向支撑,但因构件与荷载均对称,左右两个梁段之间并无相互支持作用,两个梁段的βb相等,可只取其中的一个梁段来计算。
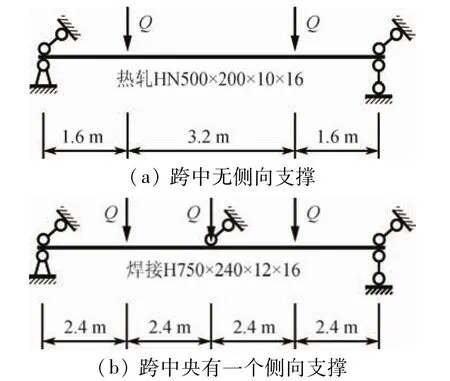
图5 横向集中荷载作用下的简支梁图

表2 荷载作用在剪心时根据不同公式得到的βb值
值得注意的是,式(7)~(11)都是根据荷载作用在构件截面剪心时的工字形截面得出的,而工程中的横向荷载普遍不作用在剪心,比如吊车梁等,因此实际适用范围仍然很有限,但各国规范中并没有提及相应的对策。
除了上述βb公式之外,杨波[21]针对双轴对称工字形截面简支梁,采用有限元法分析了一端弯矩M和上翼缘横向均布荷载q共同作用下的βb分段拟合公式,由式(12)~(14)表示为
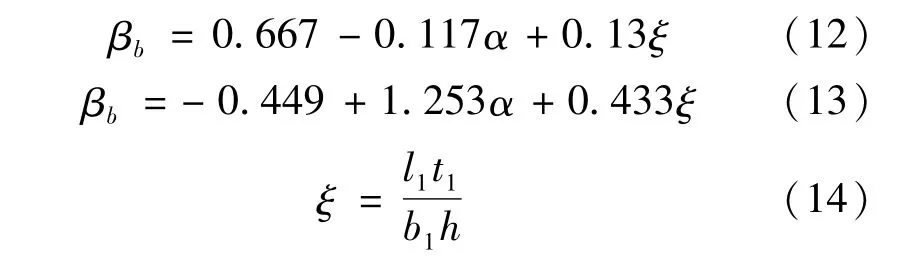
式中:α为端弯矩M与ql2/8的比值,无量纲;l为梁的跨度,m;ξ为经验参数,无量纲;l1为受压翼缘的自由长度,m;t1为受压翼缘的厚度,m;b1为受压翼缘的自由宽度,m;h为梁截面高度,m。
周芬等[22]针对双轴对称工字形截面简支梁,采用能量法推导了上翼缘均布荷载q、下翼缘跨中央集中荷载Q作用下的βb分段拟合公式,由式(15)、(16)表示为

式中:α为集中荷载Q与ql的比值,无量纲。
式(12)~(16)虽然可以考虑荷载作用点不在剪心时的影响,但荷载的形式比较特殊,适用范围很有限,只能作为一种补充。
3.2 任意侧向支撑下的简支梁
当跨中设有不等间距的任意侧向支撑时,短梁段的线刚度较大,长梁段的线刚度较小,长梁段有先于短梁段发生整体失稳的趋势,相邻的短梁段必然会对长梁段提供约束支持作用,最终同步发生失稳,这使得梁的弹性屈曲分析非常复杂。由于研究资料匮乏,目前各国普遍采用下述简化法[19,29]来计算任意侧向支撑下简支梁的弹性临界弯矩:
(1)将侧向支撑间的各梁段看作独立的简支梁;
(2)采用式(3)来分别计算各梁段的临界弯矩,当梁段的弯矩呈线性变化时βb采用式(4)、(5)来计算,当梁段的弯矩呈非线性变化时βb采用式(8)或(9)来计算;
(3)将全部梁段中最小的临界弯矩作为整个构件的临界弯矩。
依据上述简化方法得到临界弯矩显然由最弱的梁段控制,由于忽略了相邻梁段对最弱梁段提供的支持作用,所得临界弯矩必然偏低,这是偏于安全的,但有时会过于保守。
4 复杂条件下Mcr计算的简化法存在的问题、影响及根源
对于复杂荷载或侧向支撑条件下的弹性简支梁,各国规范提供的计算Mcr简化法要么假设横向荷载作用在截面剪心,要么忽略了相邻梁段间的相互支持作用,计算结果必然有偏差,下面逐一举例分析。
4.1 荷载作用点位置的影响
从前面可以看出,任意荷载及侧向支撑条件下的简化法均采用了式(3)来计算Mcr,仅是βb的计算方法不同。式(3)原本是由端弯矩作用下的简支梁得出的[13],不涉及横向荷载,也就没有荷载作用点位置的问题,而任意荷载下势必涉及到横向荷载,也就有荷载作用点位置问题。为能够继续利用式(3),各国规范推荐的相对应βb公式无不假设荷载作用在构件的截面剪心,这是合适的,但也回避了荷载作用点位置的问题。
荷载作用点位置对Mcr的影响很大[10],仍以图5所示的两个简支梁为例,利用式(3)、(8)计算的荷载作用在不同位置时的Mcr和修正[29]计算的Mcr见表3,其中括号内为与有限元解的误差百分比。由表3可以看出:当荷载作用在剪心时,误差很小且略偏安全;当荷载作用在上、下翼缘时,误差接近±30%,偏高和偏低现象并存,偏低尚可允许,偏高则会带来安全隐患。

表3 荷载作用点位置对Mcr的影响/(kN·m)
为解决上述问题,陈绍蕃[29]提出了一种修正方法,将式(8)分别乘以调整系数0.75、1.5来考虑荷载作用点位置的影响,可由式(17)、(18)表示为
荷载作用在上翼缘时
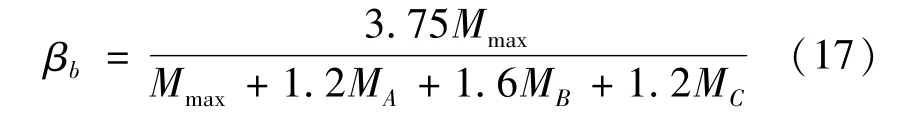
荷载作用在下翼缘时
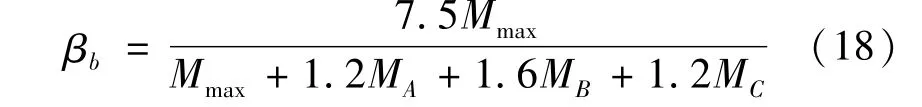
利用上述修正方法计算的Mcr,见表3。用于图5(a)构件时尽管误差不大,但仍然存在正偏差;用于图5(b)构件时误差较大的现象依然存在,甚至偏高30%,可见该方法只能用于一些特定情况,并没有彻底解决问题。
4.2 相邻梁段间的支持作用
当简支梁跨中设有侧向支撑时,如果相邻梁段的长度或弯矩图不相同,各梁段的侧向抗弯和抗扭能力也不同,有强有弱,导致梁段间存在相互支持作用,由于简化法忽略了该支持作用,所得Mcr必然偏低。
以图6所示跨中设有一个侧向支撑的均匀受弯简支梁为例,利用式(3)、(5)得到的Mcr和修正法[27-28]计算的Mcr见表4,其中括号内为与有限元解的误差百分比,可见偏低幅度在30%以上,虽无安全问题,但明显过于保守,侧向支撑分布越不均匀,梁段间的支持作用越显著,简化法越保守。
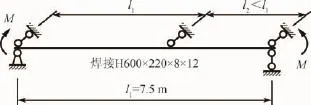
图6 侧向支撑不等间距时的均匀受弯简支梁图

表4 梁段间支持作用对Mcr的影响/(kN·m)
考虑梁段间支持作用的研究资料也不多,目前较简便的方法是修正法,在式(3)的基础上引入梁段的计算长度系数μ来对Mcr进行修正。修正后的Mcr可由式(19)表示为
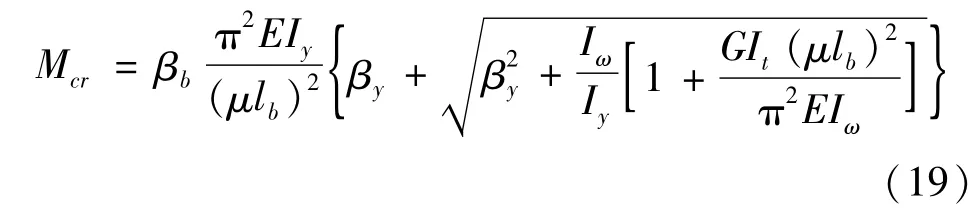
式中:μ为用来考虑梁段间支持作用的计算长度系数,无量纲;lb为所计算梁段的长度,m。
Nethercot等[27]、Tong等[28]都提供了确定μ的方法,两种方法区别不大,都是借鉴了有侧移框架柱μ的计算方法,也就是把弱梁段比作框架柱,把相邻的左右梁段比作框架梁,通过其线刚度的比值来计算μ,具体过程如下:
(1)先把侧向支撑间的各梁段按独立的简支来考虑,利用式(3)、(8)可以计算出各梁段的临界弯矩。
(2)找出临界弯矩最小的梁段,该梁段称为最弱梁段,为了便于解释,这里假设第i个梁段为最弱梁段,其临界弯矩记作Mcr,i,相邻左右梁段的临界弯矩分别记作Mcr,i-1、Mcr,i+1。
(3)按式(20)~(22)分别计算最弱梁段及相邻梁段的线刚度αi、αi-1及αi+1。
最弱梁段

相邻的第i-1梁段
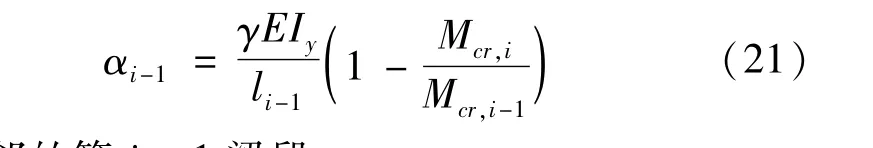
相邻的第i+1梁段

式中:li、li-1、li+1分别为第i、i-1、i+1梁段的几何长度,m;γ为线刚度调整系数,无量纲,当远端铰接时γ=3,远端固接时γ=4,远端为连续梁时γ=2。
(4)利用式(23)计算相邻梁段的线刚度之比K1、K2,然后再由式(24)计算最弱梁段的计算长度系数μ。
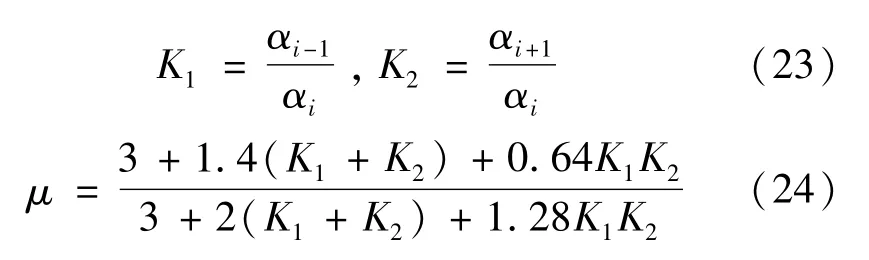
仍以图6所示简支梁为例,按上述修正法计算的临界弯矩见表4,可以看出,修正法比简化法有一定的进步。由于式(19)是基于式(1)、(3)得到的,修正法同样无法考虑横向荷载作用点位置的影响。
4.3 简化法对整体稳定系数的影响
工程设计中,受弯构件的整体稳定都是通过稳定系数φb来计算的,目前世界各国规范普遍借鉴轴压构件的柱子曲线来构建受弯构件的φb—λb曲线[2,4],如图7所示,λb为受弯构件的正则化长细比,无量纲。
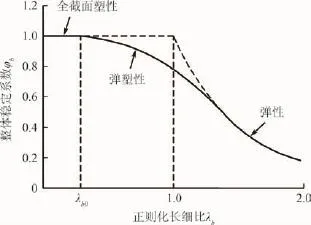
图7 受弯构件的φb—λb曲线图
规范修订报批稿借鉴欧洲和日本的方法并结合我国国情给出的φb—λb曲线可由式(25)、(26)表示为

式中:λb0为初始正则化长细比,无量纲;n为与截面类型和成型方式有关的参数,无量纲;γx为对强轴的截面塑性发展系数,无量纲;Wx为按受压翼缘确定的绕强轴的毛截面模量,m3;fy为钢材的屈服强度,N/m2。钢结构设计规范修订报批稿给出了参数λb0和n的查用表格及计算方法,不再罗列。
由式(25)、(26)可以看出,Mcr准确与否将直接影响φb值。仍以图5、6所示的简支梁为例(假设材料均为Q235),将表3、4中各种方法计算的Mcr代入式(25)、(26)后,所得φb见表5、6,其中括号内为与有限元解的误差百分比。可以看出,现有简化方法、修正方法引起的φb误差同样不可忽略,而且仍然存在正偏差情况,意味着偏于不安全,应引起足够的重视。
4.4 问题的根源
式(3)原本是利用能量法分析端弯矩作用下跨中无侧向支撑的简支梁所得到的结论,采用的总势能公式[7]、构件弯矩表达式、构件侧向弯曲变形、扭转变形表达式可分别由式(27)~(30)[13]表示为

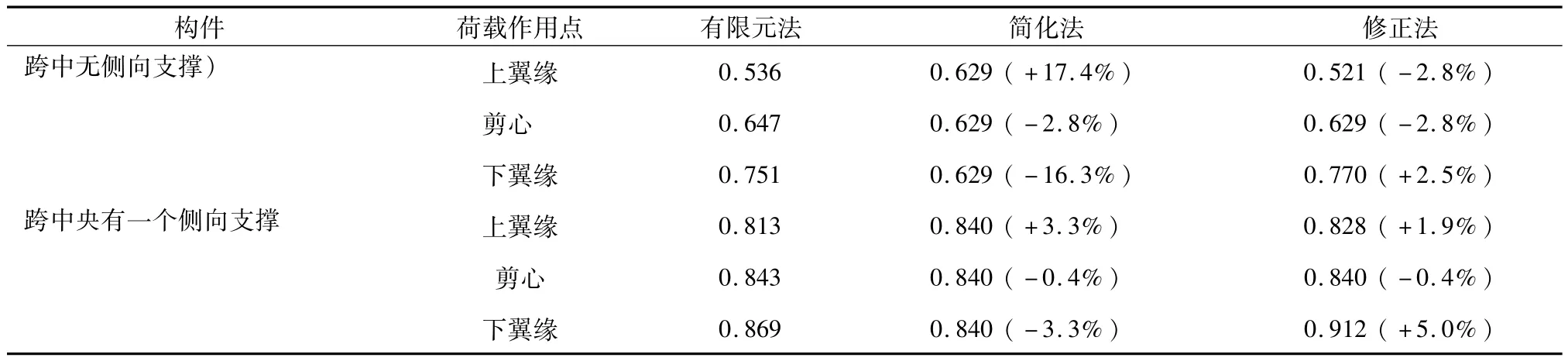
表5 现有方法计算图5构件所得φb

表6 现有方法计算图6构件所得φb

式中:Π为总势能,J;z为构件的纵向坐标,m,如图1所示;M为z坐标处的截面弯矩,N·m;u为z坐标处截面剪心的侧向位移,m;θ为z坐标处截面绕剪心的扭转角,rad;A1、A2、B分别为侧向弯曲变形函数和扭转变形函数的独立参数(广义坐标),无量纲。
由于式(28)能够准确描述构件的弯矩,式(29)、(30)描述的侧向弯曲和扭转变形形式也与构件的实际变形相匹配,因此代入式(27)后得到的式(3)是比较精确的。但是简化方法将式(3)推广至任意条件下的简支梁时,存在以下缺陷:
(1)任意条件下简支梁的弯矩表达式、侧向弯曲和扭转变形函数不可能与式(28)~(30)完全一致,因此结构应变能有差别,必然影响总势能;
(2)端弯矩作用下的简支梁不涉及横向荷载,式(27)中也就没有横向荷载产生的外力势能项,而任意条件下涉及横向荷载,也就有相应的外力势能,因此总势能有差别;
(3)βb原本是用来考虑荷载形式(端弯矩比值)和截面类型对Mcr影响的参数,若再令其兼顾考虑荷载作用点位置、梁段间支持作用等对Mcr的影响,很难实现。
由此可见,由上述缺陷引发的一系列问题不可能仅通过修正βb或者增加μ等简单方法就能解决,甚至有可能顾此失彼。
5 展望
目前简单条件下简支梁的弹性临界弯矩计算方法已比较准确,而复杂条件下简支梁的弹性临界弯矩计算方法还不完善,各国规范不得不采用简化法,这导致计算结果可能偏低也可能偏高,直接影响整体稳定系数,进而影响到结构的安全性和经济性,需引起足够的重视。
复杂条件下简支梁的弹性临界弯矩可以采用能量法来求解,今后的主要研究方向是找出能够模拟任意荷载及侧向支撑条件下简支梁的通用侧向弯曲变形函数、通用扭转变形函数以及通用弯矩表达式,这样才能精确计算出简支梁的总势能,从而得到复杂条件下简支梁的临界弯矩通用表达式及高精度解。由于能量法已经全面考虑了各种可能的影响因素,无需再对计算结果进行修正或调整,可以从根本上彻底解决问题。
找到简支梁的通用侧向弯曲变形函数、通用扭转变形函数相对容易,可以采用由多个可能位移函数通过线性组合而成的多项式来表达,其中可能位移函数可采用三角函数的形式。变形函数的多项式不宜超过两项,否则计算总势能时过于复杂,得到的临界弯矩表达式会比较繁琐,给使用带来不便。另外,变形函数应至少满足位移边界条件,如果还能同时满足力学边界条件,则计算精度会更高。
找到简支梁的通用弯矩表达式则有一定的困难。由于简支梁的荷载类型、数量及位置复杂多变,弯矩图也随之变化,如果不给定具体的荷载类型、数量及位置,则很难写出弯矩表达式,也就不能进行总势能计算。一旦给定了具体的荷载类型、数量及位置,虽然可以写出弯矩的准确表达式,但又不具备通用性,这是一对矛盾,相信工程界和学术界总会找到合适的解决办法。
参考文献:
[1] 郭彦林.纯弯等截面焊接工字形梁整体稳定系数研究[J].建筑科学与工程学报,2012,29(2):89-95.
[2] 童根树.钢梁稳定性再研究:中国规范的演化及其存在问题(Ⅰ)[J].工业建筑,2014,44(1):149-153.
[3] 童根树.钢梁稳定性再研究:国际上的试验研究和理论分析(Ⅱ)[J].工业建筑,2014,44(2):142-146.
[4] 童根树.钢梁稳定性再研究:国际上规范对比及其可靠度分析(Ⅲ)[J].工业建筑,2014,44(3):162-168.
[5] 童根树.钢梁稳定性再研究:国内近年的研究成果和建议(Ⅳ)[J].工业建筑,2014,44(4):146-151.
[6] 丁阳,郭鹏.高强钢焊接工字梁整体稳定性能分析[J].建筑结构,2015,45(21):25-29.
[7] Bleich F..Buckling Strength of Metal Structures[M].New York:McGraw-Hill,1952.
[8] 吕烈武,沈世钊,沈祖炎,等.钢结构构件稳定理论[M].北京:中国建筑工业出版社,1983.
[9] 童根树.钢结构的平面外稳定(修订版)[M].北京:中国建筑工业出版社,2013.
[10]陈骥.钢结构稳定理论与设计(第6版)[M].北京:科学出版社,2014.
[11]童根树,张磊.薄壁钢梁稳定性计算的争议及其解决[J].建筑结构学报,2002,23(3):44-51.
[12]郭耀杰,方山峰.钢结构构件弯扭屈曲问题的计算和分析[J].建筑结构学报,1990,11(3):38-43.
[13]Salvadori M.G..Lateral buckling of eccentrically loaded I-columns[J].Transactions of the American Society of Civil Engineers,1956,121(1):1163-1178.
[14]Kirby P.A.,Nethercot D.A..Design for Structural Stability[M].Suffolk:Constrado Monographs,1979.
[15]罗金辉,李元齐.均布荷载作用下有约束钢梁的整体稳定[J].南昌大学学报(工科版),2012,34(3):224-228.
[16]Greiner R.,Lindner J..Proposals for buckling resistance of members[R].Flexural and Lateral Torsional Buckling,ECCS Validation Group,1992.
[17]Suryoatmono B.,Ho D..The moment-gradient factor in lateraltorsional buckling on wide flange steel sections[J].Journal of Constructional Steel Research,2002,58(9):1247-1264.
[18]Serna M.A.,López A.,Puente I.,et al..Equivalent uniform moment factors for lateral-torsional buckling of steelmembers[J]. Journal Constructional Steel Research,2006,62(6):566-580.
[19]陈骥.各国钢结构设计规范中受弯构件稳定设计的比较[J].工业建筑,2009,39(6):5-12.
[20]罗金辉,顾强,方有珍.端弯矩及横向均布荷载共同作用下钢梁的整体稳定研究[J].钢结构,2009,24(增刊1):148-152.
[21]杨波.工字梁在弯矩和均布荷载作用下的整体稳定[J].钢结构,2012,27(11):23-25,86.
[22]周芬,池云祥,杜运兴.上下翼缘同时受荷的工字形钢梁整体稳定性分析[J].湖南大学学报(自然科学版),2012,39(11):7-12.
[23]周绪红,刘占科,陈明,等.钢梁弯扭屈曲临界弯矩通用公式研究[J].建筑结构学报,2013,34(5):80-86.
[24]刘占科,周绪红,何子奇,等.复合荷载作用下简支钢梁弹性弯扭屈曲研究[J].建筑结构学报,2014,35(4):78-85.
[25]管海龙,郭兵,褚昊.复合荷载下简支梁的弹性弯扭屈曲[J].山东建筑大学学报,2016,31(3):249-253.
[26]褚昊,郭兵,管海龙.单个移动集中荷载下简支梁的弹性临界弯矩[J].山东建筑大学学报,2016,31(5):466-470.
[27]Nethercot D.A..Buckling of laterally or torsionally restrained beams[J].Journal of the Engineering Mechanics Division,ASCE,1973,99(4):773-791.
[28]Tong G.S.,Chen S.F..Buckling of laterally and torsionally braced beams[J].Journal of Constructional Steel Research,1988,11(1):41-55.
[29]陈绍蕃.有约束梁的整体稳定[J].钢结构,2008,23(8):20 -25,41.
[30]GB 50017—201X,钢结构设计规范(报批稿)[S].北京:中国计划出版社,2012.
[31]Clark J.W.,Hill H.N..Lateral buckling of beams[J].Journal of Structural Division,1960,86(ST7):175-196.
Research process of elastic criticalmoment of sim ple beam s
Guo Bing1,Sun Naiyi2,Yang Dabin1
(1.School of Civil Engineering,Shandong Jianzhu Univesity,Jinan 250101,China;2.Rongcheng Supervision and Management Station of Construction Engineering Quality and Cost,Rongcheng 264300,China)
The overall stability coefficient is an importantbasis for calculating the structure just by the overall stability of bendingmember.Elastic criticalmoment is themain factor affecting the diameter of the overall stability coefficient so the accuracy directly affects the stability of the calculation results. The calculation method of critical elastic moment of simple beam under simple conditions is accurate method,but the application scope is limited;the calculationmethod of criticalmomentof elastic beam under complex conditions is the simplified method,and the criticalmoment for beam arbitrary loading and lateral support conditions,only to simplify the calculation bymeans of equivalentbendingmoment coefficient.This paper expounds the simple conditions,exact method under complex load under complicated conditions,exact method simplified method of different load conditions for the critical moment of criticalmomentmethod and the research progress in influence factors through the research on the position of the loading pointand the adjacent beam segmentbetween the supportand the overall stability coefficient under the influence of the simplified method under complex conditions elastic criticalmoment calculation problems and causes.and makes prospect for the energy method for the calculation of criticalmoment of elastic beam under complex conditions.
simple beams;elastic critical moment;simplified method;equivalent moment coefficient;total potential energy
TU391
A
1673-7644(2017)01-0069-09
2016-12-23
国家自然科学基金项目(51308326)
郭兵(1970-),男,教授,博士,主要从事钢结构等方面的研究.E-mail:sdgb123@163.com
