线性模型中的加权混合几乎无偏两参数估计

左卫兵， 康萃雯

(华北水利水电大学 数学与信息科学学院，河南 郑州 450046)

线性模型中的加权混合几乎无偏两参数估计

左卫兵， 康萃雯

(华北水利水电大学 数学与信息科学学院，河南 郑州 450046)

主要讨论了随机约束线性模型的有偏估计问题,提出了一种新的加权混合几乎无偏两参数估计.证明了加权混合几乎无偏两参数估计在二次偏差的准则下优于加权混合两参数估计,并给出了在均方误差矩阵准则下新估计优于其他相关估计的充要条件.

加权混合两参数估计；加权混合几乎无偏两参数估计；二次偏差；均方误差矩阵

0 引言

考虑含随机约束线性模型

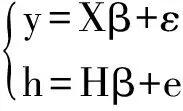
(1)

其中y是n维观测向量,X为n×p的列满秩设计阵,β是p维未知参数向量,ε是n维误差向量,且E(ε)=0,E(εεT)=σ2I,I是n阶单位矩阵.H为r×p行满秩矩阵,e为随机扰动项且E(e)=0,Cov(e)=σ2W,W为已知正定阵.

模型(1)的研究起源于文献[1]提出的普通混合估计,当先验信息和样本信息重要性不一致时,文献[2]提出了加权混合估计.但当模型存在多重共线性时,混合估计存在明显不足.因此,目前诸多学者通过把不同估计结合起来探讨新的估计,这些估计比原估计更优.文献[3-4]将混合估计分别与Liu估计和岭估计结合,提出了随机约束Liu估计和随机约束岭估计,文献[5-6]将加权混合估计分别与Liu和几乎无偏岭估计结合,得到了加权混合Liu和加权混合几乎无偏岭估计,文献[7]在文献[8]的基础上将两参数估计算子作用于混合估计,提出了随机约束两参数估计.本文通过将几乎无偏两参数估计引入到加权混合估计中,提出了加权混合几乎无偏两参数估计,并在均方误差矩阵准则下与现有的加权混合估计等进行优良性比较.

1 新估计的提出

对于模型(1),文献[2]提出了加权混合估计,其定义为

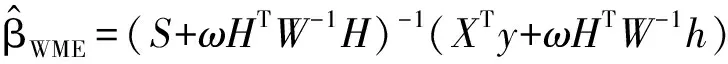
(2)

其中S=X′X,ω(0<ω<1)为常数权重系数.对于不带约束的线性模型,文献[9]通过组合岭估计和Liu估计提出了一种新的两参数估计，

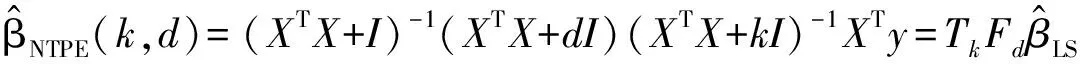
(3)

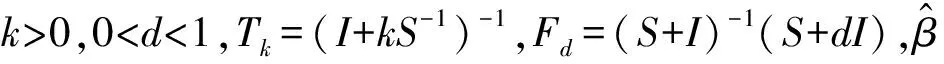
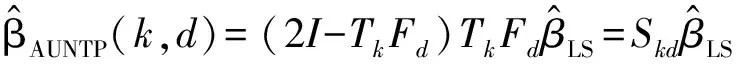
(4)

其中可定义Skd为几乎无偏两参数估计算子.

对于带随机约束的线性模型,本文将定义的新的两参数估计算子和几乎无偏两参数估计算子分别作用于加权混合估计,提出了如下的加权混合两参数估计和加权混合几乎无偏两参数估计，

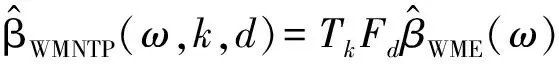
(5)

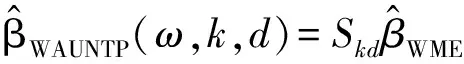
(6)

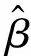
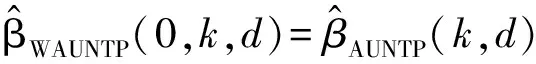
(7)

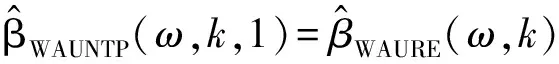
(8)

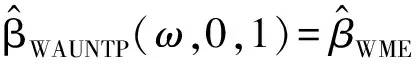
(9)

2 偏差比较

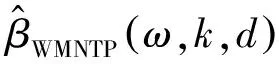
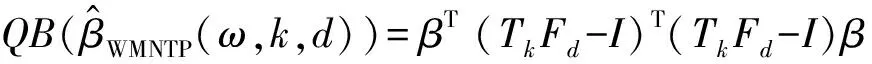
(10)

(11)

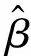
βT[(TkFd-I)T(TkFd-I)-(Skd-I)T(Skd-I)]β.

(12)

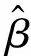
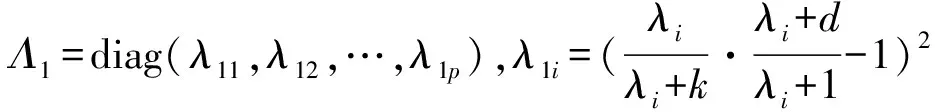
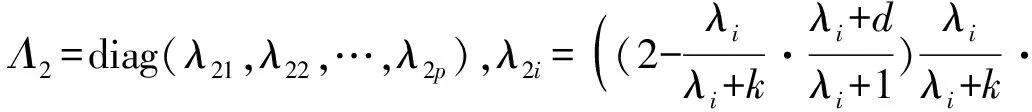
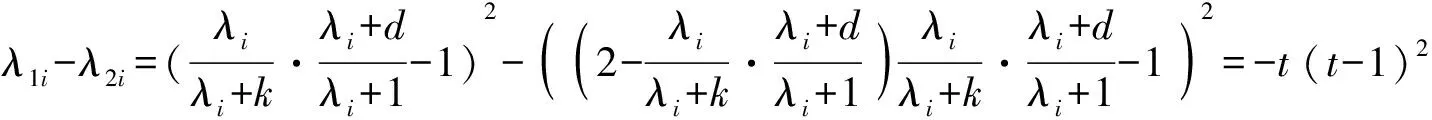
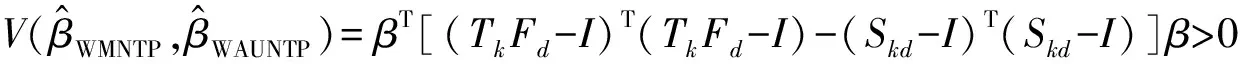
由上述定理知,加权混合几乎无偏两参数估计是对加权混合两参数估计的偏差进行矫正的估计.

3 均方误差矩阵比较

为了进一步考虑在偏差和方差共同作用下新估计的优良性,我们利用均方误差矩阵准则MSEM,将其与相关估计进行比较.记A=(S+ωHTW-1H)-1,

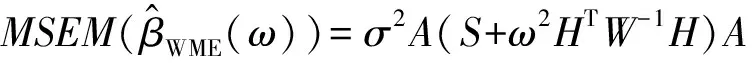
(13)

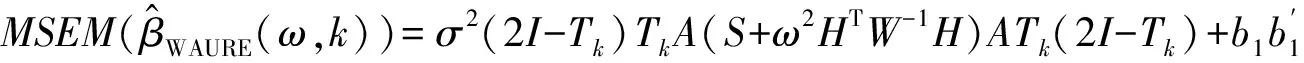
(14)

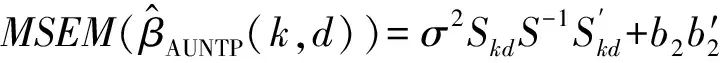
(15)

(16)

其中b1=[(2I-Tk)Tk-I]β=-(Tk-I)2β,b2=[(2I-TkFd)TkFd-I]β=-(TkFd-I)2β,b3=b2.

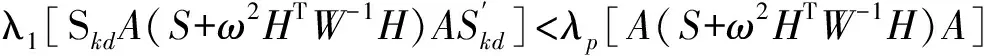
证明 由式(13)和式(16)可得

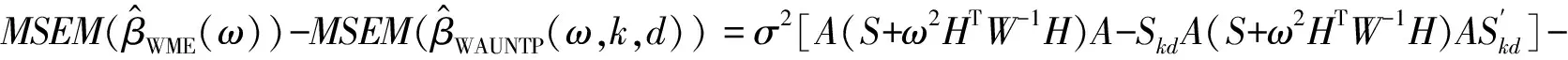
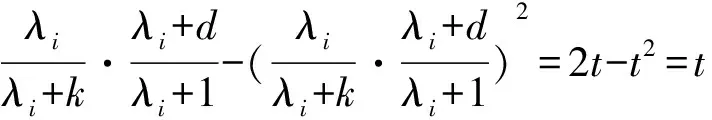
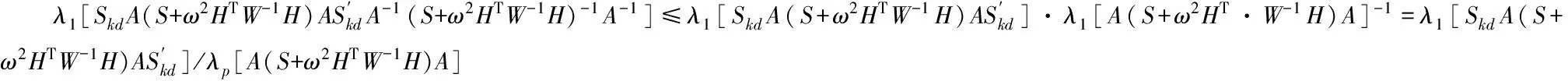
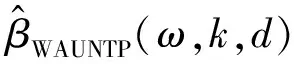
证明 由式(14)和式(16)可得

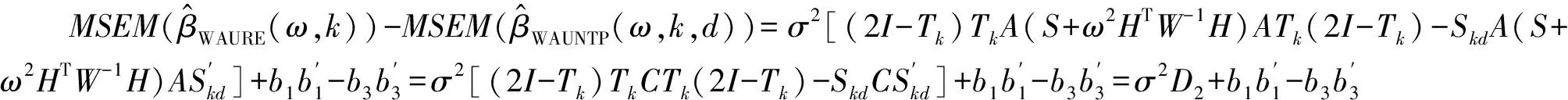
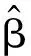
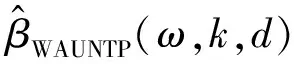
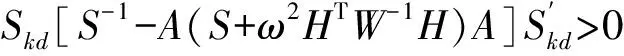
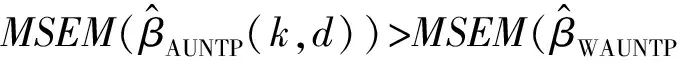
4 数据模拟

为了说明上述估计的性质,这一节我们用具体的数据来分析.本文进行如下数据模拟,数据来源于文献[14],数据如下：

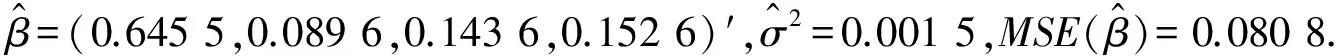
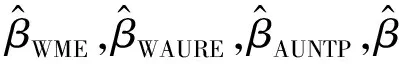
表和的均方误差 (ω=0.2)

表和的均方误差 (ω=0.4)

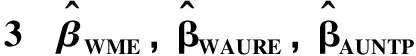
表和的均方误差 (ω=0.7)

5 结论

本文针对带有随机约束线性模型的参数估计问题,在加权混合估计和几乎无偏两参数估计的基础上,提出了加权混合几乎无偏两参数估计,并在二次偏差和均方误差矩阵准则下,对新估计和相关估计进行了比较分析,结果表明加权混合几乎无偏两参数估计在二次偏差准则下一致优于加权混合两参数估计,而在均方误差矩阵准则下分别优于加权混合估计,加权混合几乎无偏岭估计,几乎无偏两参数估计的充要条件,最后通过数据模拟计算验证了我们的结论.

[1] THEIL H. On the use of incomplete prior information in regression analysis[J]. Journal of the American Statistical Association, 1963, 58(302):401-414.

[2] TRENKLER G, TOUTENBURG H. Mean squared error matrix comparisons between biased estimators： An overview of recent results[J]. Statistical Papers, 1990, 31(1):165-179.

[3] HUBERT M H, WIJEKOON P. Improvement of the Liu estimator in linear regression model[J]. Statistical Papers, 2006, 47(3):471-479.

[4] LI Y, YANG H. A new stochastic mixed ridge estimator in linear regression model[J]. Statistical Papers, 2010, 51(2):315-323.

[5] 杨虎, 殷艺芸. 线性模型中一种新的随机加权混合Liu估计[C]// 中国现场统计研究会第十五届学术年会, 2012: 253-256.

[6] 刘朝林, 荣腾中, 赵菲,等. 一种基于随机约束线性模型的参数有偏估计[J]. 统计与决策, 2014(13): 75-77.

[7] YANG HU, WU JIBO. A stochastic restrictedk-dclass estimator [J]. Statistics A Journal of Theoretical & Applied Statistics, 2012, 46(6):1-8.

[8] OZKALE M, KACIRANLAR S. The restricted and unrestricted two-parameter estimators[J]. Communication in Statistics Theory and Methods, 2007, 36(15):2707-2725.

[9] YANG HU, CHANG XINFENG. A new two-parameter estimator in linear regression [J]. Communication in Statistics Theory and Methods, 2010, 39(6):923-934.

[10]常新锋, 晋守博. 线性模型参数的几乎无偏两参数估计 [J]. 统计与决策, 2014(16):25-27.

[11]RAO C R, DR SHALABH, TOUTENBURG H, et al. Linear models and generalizations, least squares and alternatives[J]. 3rd Ed. Advances in Statistical Analysis, 2009, 93(1):121-122.

[12]FAREBROTHER R W. Further results on the mean square error of ridge regression [J]. Journal of the Royal Statistical Society, 1976, 38(3):248-250.

[13]TRENKLER G, TOUTENBURG H. Mean squared error matrix comparisons between biased estimators： An overview of recent results [J]. Statistical Papers, 1990, 31(1):165-179.

[14]AKDENIZ F, EROL H. Mean squared error matrix comparisons of some biased estimator in linear regression [J]. Communications in Statistics Theory and Methods, 2003, 32(12): 2389-2413.

Weighted Mixed almost Unbiased Two Parameter Estimator in Linear Regression Model

ZUO Weibing, KANG Cuiwen

(CollegeofMathematicsandInformationScience，NorthChinaUniversityofWaterResourcesandElectricPower，Zhengzhou450046，China)

Some biased estimators of random restricted linear regression model were discussed and a new weighted mixed almost unbiased two parameter estimator was proposed. Furthermore, proved that the new estimator performed better than weighted mixed two parameter estimator under the rule of quadratic deviation. Under the mean square error matrix criterion, the necessary and sufficient conditions for the new estimator to be superior to other estimators were given out.

weighted mixed two parameter estimator; weighted mixed almost unbiased two parameter estimator; quadratic deviation; mean square error matrix

2016-10-26

河南省基础与前沿技术研究项目(142300410401)

左卫兵(1976—)，男，河南内黄人，华北水利水电大学数学与信息科学学院教授，主要研究方向：数理统计.

10.3969/j.issn.1007-0834.2017.01.001

O212.1

A

1007-0834(2017)01-0001-05