云南省低纬度高原季风气候条件下不同方法计算ET0的对比研究
2017-04-12侯铭欣王新华
侯铭欣++王新华
摘要:为了探求4种不同参照作物需水量(ET0)计算方法在云南省低緯度高原季风气候区的适用性,根据云南省丽江气象站1980~2005年的气象资料,以Penman-Monteith公式计算结果为参照标准,通过Makkink公式、Hargreaves公式和Priestley-Taylor公式计算了ET0,分别对每个公式所得的年值和月值的绝对偏差、平均偏差和相对偏差等进行分析对比。结果表明,3种公式的计算精度排序为Makkink公式 关键词:参照作物需水量;低纬度高原季风气候;回归方程;云南省 中图分类号:P462.4+1;S274.4 文献标识码:A 文章编号:0439-8114(2016)22-5807-04 DOI:10.14088/j.cnki.issn0439-8114.2016.22.020 Comparison of Estimating ET0 with Different Methods under the Condition of Low Latitude Plateau Monsoon Climate in Yunnan Province HOU Ming-xin, WANG Xin-hua (College of Water Conservancy, Yunnan Agricultural University, Kunming 650201, China) Abstract:In order to obtain the proper calculation methods for reference crop evapotranspiration(ET0) under the condition of low latitude plateau monsoon climate in Yunnan province,three calculation methods (Makkink formula,Hargreaves formula and Priestley-Taylor formula) were used to compute ET0 based on the climate data from 1980-2005 at Lijiang weather station. And an comparison analysis of absolute error,average error and relative error of annual value and monthly value was made between reaults of these three formulas and Penman-Monteith formula was regarged as a reference. The results showed that Makkink formula had the lowest accuracy and Hargreaves eformula had the highest accuracy. In order to improve the accuracy,an equation for calculating ET0 which was fit for Yunnan province was put forward by establishing a regression equation. Key words: reference evapotranspiration; low latitude plateau monsoon climate; regression equation; Yunnan province 参照作物需水量ET0(reference crop evapotranspiration)是用以计算作物需水量的一个重要参数,其定义为在土壤水分充足、地面完全覆盖、植物生长正常的条件下,草高为8~15 cm,开阔且高矮整齐的矮草地上的蒸发量[1]。目前,ET0 的计算方法已有很多种,主要有温度法、辐射法(模型法)、蒸发皿法、经验公式法和综合法等[2,3]。其中较常用的是联合国粮农组织推荐的FAO-56 Penman-Monteith方法[4],该方法综合考虑了多种气象要素,在湿润、干旱地区适用性较强。但其所需参数较多,在气象资料短缺的地区不易获取,其应用性受到一定限制[5-7]。而对于温度法的Hargreaves公式[8],以及辐射法的Makkink公式[9]和Priestley-Taylor公式[10],需求的资料相对较少,对于资料匮乏的地区非常实用。研究者在探讨各种公式在各个地区的适用性时做了很多对比研究,例如Wu等[11]利用夏威夷的气象资料比较了计算ET0的6种不同方法,认为Hargreaves公式有较好的实用性。彭世彰等[5]比较了3种计算方法在江西的适用性,结果表明Priestley-Taylor公式最优,Hargreaves公式差异较大。中国还有较多学者对Hargreaves公式在华北、华东、西北等地区的适用性也都进行了深入探讨[12-17],但对于云南省这种低纬度高原季风气候区计算ET0方法的适用性研究还很少。对于低纬度高原气候地区,其具有四季温差小、干湿季分明、垂直差异显著、气象灾害较多等诸多特点,所以研究适于该地区参照作物需水量的计算方法是十分必要的。以云南省丽江站1980~2005年的逐月气象资料为基础,并以Penman-Monteith公式为参照标准,分别计算并验证了Hargreaves公式、Makkink公式和Priestley-Taylor公式在云南地区的适用性。
1 研究区域和资料
1.1 研究区域概况
丽江地处云南省西北部云贵高原与青藏高原的连接部位,属于低纬度高原季风气候,地理坐标东经100.25°,北纬26.86°,海拔2 400 m。总面积20 600 km2。丽江干湿季分明,一年四季均有可能发生干旱灾害,根据数据显示,平均每1.3年出现1次。
1.2 数据来源
数据来自丽江站(27°26′N,100°22′E,观测地海拔高度为2 393.2 m)1980~2005年逐月气象资料,包括月平均最高气温(Tmax)、平均最低气温(Tmin)、平均相对湿度(RH)、平均风速(u)、日照时数(n)和降雨量(P)等相关数据。
2 研究方法
2.1 计算方法
选用联合国粮农组织推荐的FAO-56Penman-Monteith公式为参照标准,用以检验Hargreaves公式、Makkink公式和Priestley-Taylor公式在云南地区的计算精度及适用性。
Penman-Monteith公式如下:
ET0(PM)=■ (1)
式中,ET0(PM)为使用Penman-Monteith公式计算的ET0(mm/d);Δ为饱和水汽压与温度曲线的斜率(kPa/℃);Rn为作物冠层表面的净辐射[MJ/(m2·d)];G为土壤热通量[MJ/(m2·d)],当计算步长为24 h时,可以忽略;T为2 m高度处的日平均气温(℃);u2为2 m高度处的风速(m/s);es为饱和水汽压(kPa);ea为实际水汽压(kPa);es-ea为饱和水汽压差(kPa);?酌为干湿表常数(kPa/℃)。
Makkink公式如下:
ET0(M)=0.61■■Rs-0.12 (2)
式中,ET0(M)为使用Makkink公式计算的ET0(mm/d);Rs为太阳辐射或短波辐射[MJ/(m2·d)]; ?酌为汽化潜热(MJ/kg),取常数2.45。其他参数同式(1)。
Priestley-Taylor公式如下:
ET0(P)=■■(Rn-G) (3)
式中,ET0(P)为使用Priestley-Taylor公式计算的ET0(mm/d);其他参数同式(1)。
Hargreaves公式如下:
ET0(H)=0.002 3Ra(T-17.8)■ (4)
式中,ET0(H)為使用Hargreaves公式计算的ET0(mm/d);Ra为与外空辐射等价的水量(mm/d);T为日平均气温(℃);Tmax为日最高气温(℃);Tmin为日最低气温(℃);0.002 3为初始公式的经验系数。
2.2 分析方法
运用SPSS统计软件分析统计变量绝对偏差d、平均偏差d、标准偏差S、相对偏差R。以此来比较分析Makkink公式、Priestley-Taylor公式及Hargreaves公式的计算精度。
3 结果与分析
3.1 ET0的年值变化比较
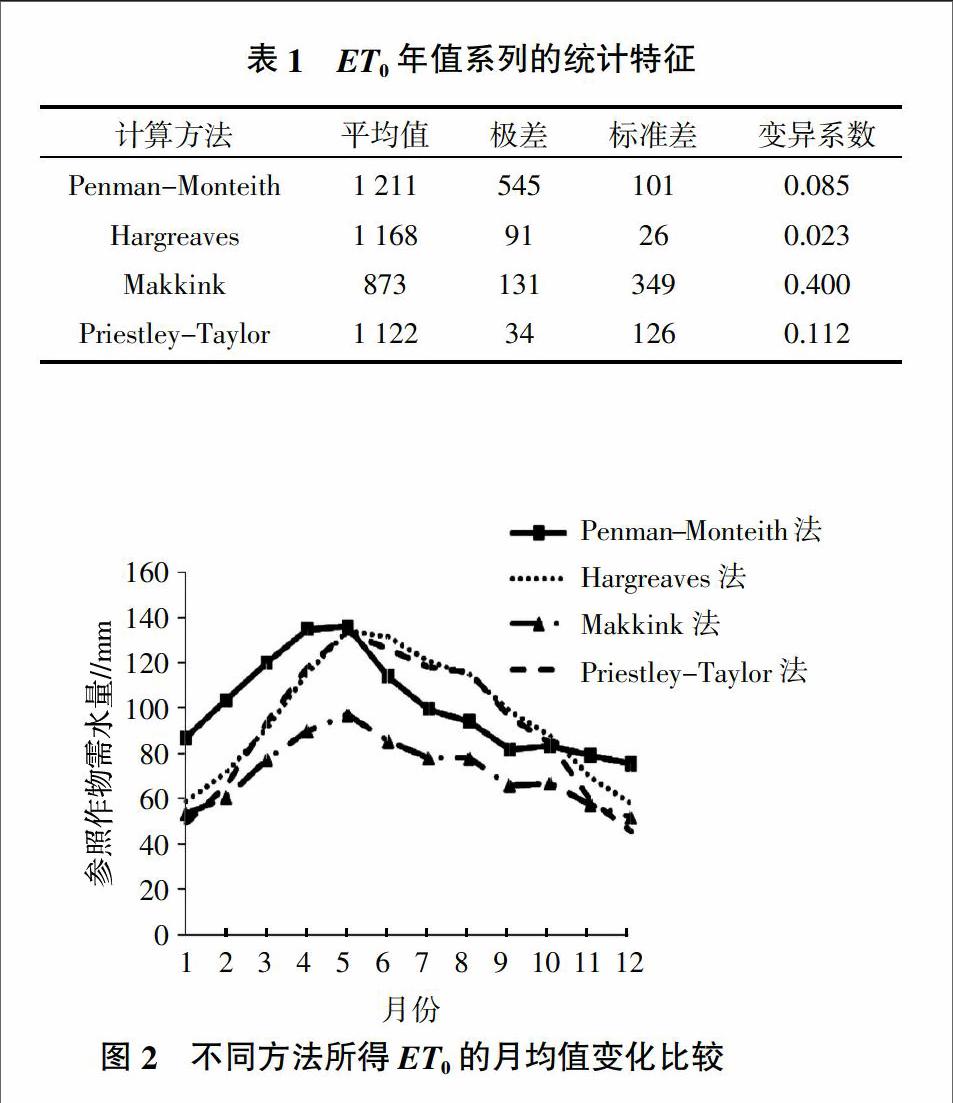
根据4种方法计算的参照作物需水量年值的对比情况(图1),可知Penman-Monteith公式、Makkink公式、Hargreaves公式、Priestley-Taylor公式的ET0量、相对误差、绝对误差。4种方法计算的ET0年值系列的平均值、极差、标准差和变异系数见表1。
由图1可知,Makkink公式与Penman-Monteith公式的计算结果偏差最大,在806.88~937.49 mm之间,其计算结果只有Penman-Monteith公式的70%左右。Hargreaves公式与Priestley-Taylor公式计算所得数据的年际变化趋势大致与Penman-Monteith公式相同。Priestley-Taylor公式的计算结果要优于Makkink公式的计算结果,在1 150.97~1 184.96 mm之间,计算值均小于Penman-Monteith公式值,绝对偏差在30.78~307.36 mm之间,相对偏差为2.7%~37.9%。Hargreaves公式的计算结果与Penman-Monteith公式计算结果较为接近。除在1990、2000和2001年之外,都比Penman-Monteith公式计算的结果小,2001年Hargreaves公式计算结果远大于Penman-Monteith公式计算的结果,1990~1993、2002~2004年期间两种方法计算结果差异较小,且1993年偏差达到最小。由Hargreaves公式计算的1980~2005年的范围在1 122~1 211 mm之间,26年平均为 1 169 mm。与Penman-Monteith法计算的ET0的绝对偏差在-148~344 mm之间,平均偏差43 mm,相对偏差在-10.9%~42.6%之间,平均相对偏差-2.8%。
由表1可知,Hargreaves公式计算结果的极差、标准差、变异系数只有Penman-Monteith公式计算结果的1/4左右,说明Hargreaves公式的年值变异性小,计算结果更稳定;Priestley-Taylor公式的结果与Penman-Monteith公式较为接近,而Makkink公式计算的ET0的标准差和变异系数都较大,与Penman-Monteith公式所得结果相差最大。
3.2 ET0的月均值的变化比较
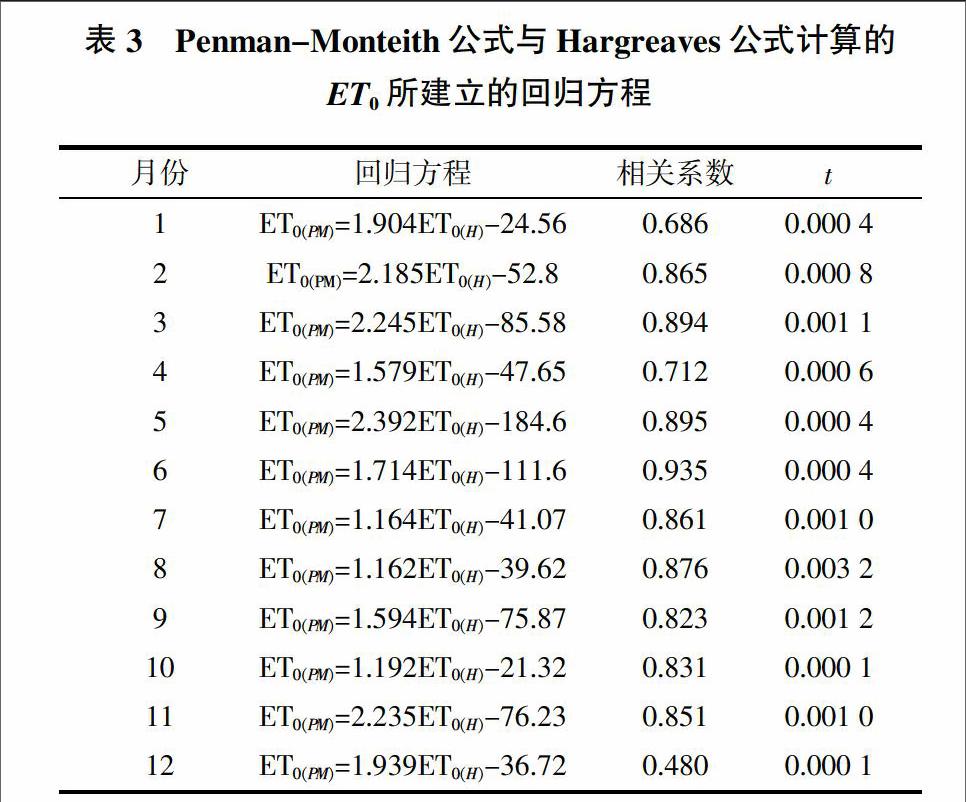
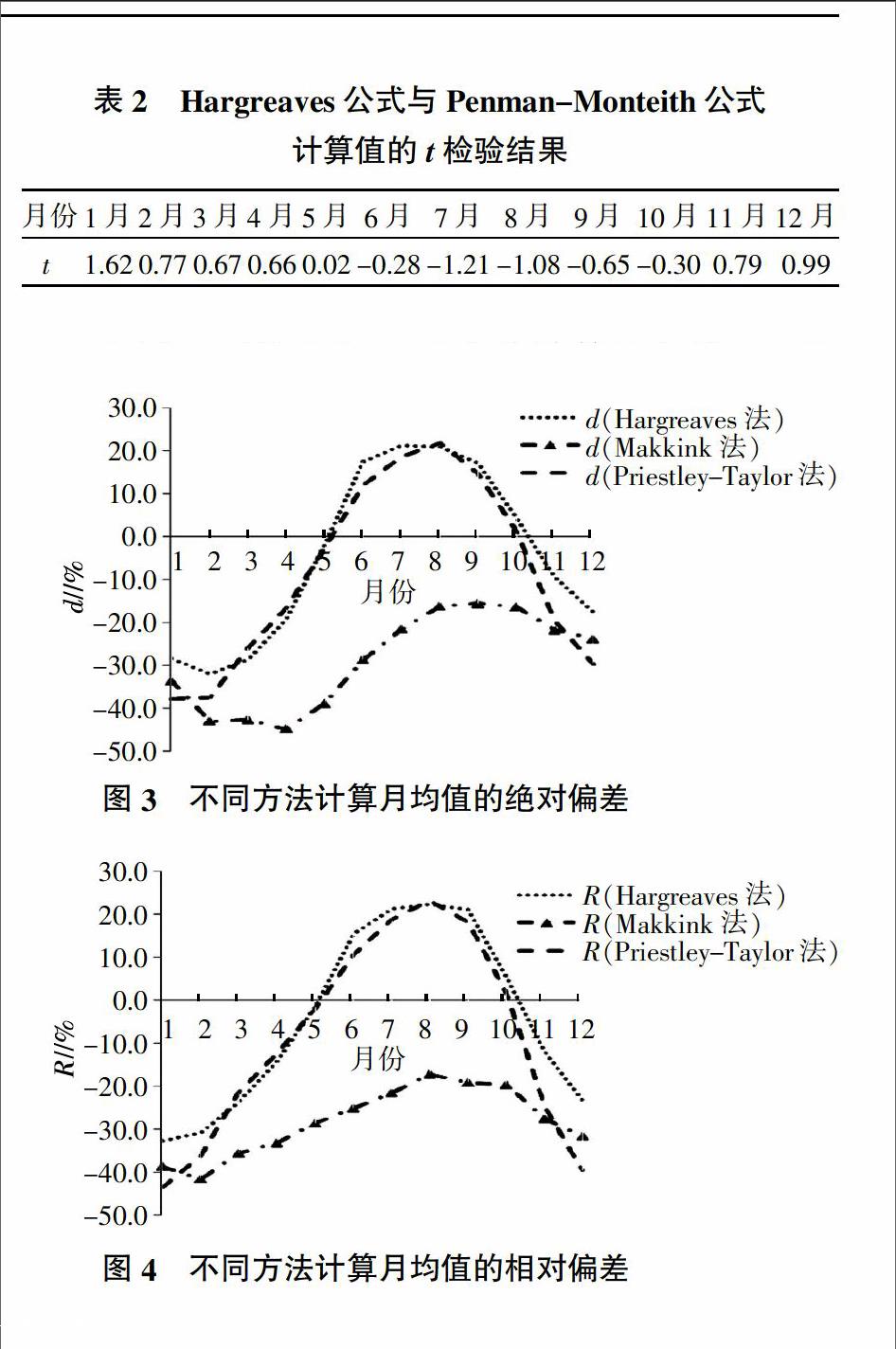
4种方法所计算的ET0的逐月平均变化比较见图2。3种方法计算月均值的绝对偏差(d)和相对偏差(R)见图3、图4。Hargreaves公式与Penman-Monteith公式计算值的t检验结果见表2。
由图2可以看出,4种方法计算所得的ET0月均值的变化趋势大体一致:均是从1月份开始逐渐升高,在5月达到最大值,然后开始下降,12月份达到最小值。其中Makkink公式计算所得月均值均小于Penman-Monteith法所得值,且存在明显差异。而Hargreaves法与Priestley-Taylor法的计算值十分接近,计算所得的ET0月均值在6、7、8、9、10月,比用Penman-Monteith公式计算的ET0大,而其他月份又比Penman-Monteith公式的值小,5月和10月二者十分接近。其结果表明在夏季雨水多、蒸发量大的月份用Hargreaves公式和Priestley-Taylor公式计算的ET0会明显偏高。
由图3、图4可以看出,Makkink公式的绝对偏差均为负值,即Makkink公式计算值均小于Penman-Monteith公式,范围在-45~-16 mm之间,从1月开始,计算结果的绝对偏差逐渐增大,到4月达到最大值,随后又逐渐减小,10月达到最小值,平均绝对偏差高达-29 mm;该公式的相对偏差在-41.6%~ -17.2%之间,最大值出现在2月,随后逐渐减小至8月的-17.2%,然后又逐渐增加到12月的-31.6%,平均相对偏差高达-28.3%。Hargreaves公式与Priestley-Taylor公式计算结果的绝对偏差大致相同,大体趋势均为1-5月绝对偏差逐渐减小。其中Hargreaves公式的绝对偏差在5月达到最小,6-8月偏差逐渐增大,8-10月又逐渐减小。Priestley-Taylor公式的绝对偏差在10月达到最小,随后两种方法的计算偏差均又逐渐增大。Hargreaves公式与Priestley-Taylor公式的绝对偏差均有正有负,Hargreaves公式介于-32~21 mm之间,平均偏差只有-5 mm。Priestley-Taylor公式的绝对偏差介于-38~22 mm之间,平均偏差也仅为-8 mm。Hargreaves公式与Priestley-Taylor公式在整个阶段的相对偏差均与它们的绝对偏差的变化趋势基本一致,有正有负。Hargreaves公式的相对偏差介于-32.7%~22.3%,平均相对偏差为-4.4%。Priestley-Taylor公式的相对偏差介于-43.6%~23.1%之间,平均相对偏差也仅为 -8.9%。由此可见,Hargreaves公式与Priestley-Taylor公式计算云南地区参照作物需水量的精度要比Makkink公式的精度高得多。
从表2可以看出,|t| 3.3 Hargreaves公式的修正 以丽江地区26年的气象资料为依据,利用不同方法计算的ET0对比分析可以发现,虽然Makkink法在计算过程中较Penman-Monteith法需要的参数少,但由于其公式的局限性,造成计算精度不高;而Priestley-Taylor公式与Hargreaves公式计算结果相近,且Hargreaves公式计算精度略高于Priestley-Taylor公式。为了进一步提高Hargreaves公式的计算精度,且为今后云南地区更精确地估算ET0做参考,将Hargreaves公式与Penman-Monteith公式的计算结果进行比较,发现二者具有较好的相关关系,因此建立逐月的回归方程,结果见表3。 经过t检验发现,修正后的Hargreaves公式计算的所有月份的|t| 4 结论 经对比分析发现,Hargreaves公式与Priestley-Taylor公式的计算精度相近,且远高于Makkink公式的计算精度,其中Hargreaves公式的计算精度最高。为使Hargreaves公式更精确地计算云南地区的ET0,对其建立了回归方程,结果显示计算精度进一步提高,且该回归方程可以替代Penman-Monteith公式在该地区使用。 参考文献: [1] 郭元裕.农田水利学[M].北京:中国水利水电出版社,1997. [2] 王声锋,汪顺生,段爱旺,等.豫西北几种ET0计算方法的比较及Hargeaves公式的修正[J].灌溉排水学报,2010,29(6):29-33. [3] 陈玉民,郭国双,王广兴,等.中国主要作物需水量与灌溉[M].北京:水利电力出版社,1995. [4] ALLEN R G,PEREIRA L S,RAES D,et al.Crop evapotranspiration guidelines for computing crop water requirements irrigation and drainage paper[M].Rome:FAO,1998:1-300. [5] 彭世彰,徐俊增.参考作物蒸发蒸腾量计算方法的应用比较[J].灌溉排水学报,2004,23(6):5-9. [6] 左德鹏,徐宗学,刘兆飞.基于气温的潜在蒸散发量估算方法在我国西北干旱地区的应用比较[J].干旱区资源与环境,2009, 23(10):123-131. [7] ALLEN R G,PEREIRA L S,RAES D,et al.Crop evapotranspiration-guidelines for computing crop water requirements FAO irrigation and drainage[M].Rome:FAO,1998. [8] HARGREAVES G H,ALLEN R G. History and evaluation of Hargreaves evapotranspiration equation[J].Journal of Irrigation Drainage Engineering,2003,130(5):53-63. [9] MAKKINK G F.Testing the Penman formula by means of lysimeters[J].Journal of the Institution of Water Engineers,1957,11(3):277-288. [10] PRIESTLEY C H B,TAYLOR R J.On the assessment of surface heat flux and evaporation using large-scale parameters[J].Monthly Weather Review,1972,100(2):81-92. [11] WU I P.A simple evapotranspiration model for Hawaii:The Hargreaves model[A].CTAHR F S. Engineer' s Notebook[M]. Manoa:Agric &Human Resour,University of Hawaii,1997. [12] 冯克鹏,田军仓.Hargreaves公式计算宁夏地区参考作物腾发量的研究[J].干旱区资源与环境,2014,28(9):100-105. [13] 刘宏伟,余钟波.用Hargreaves法与Penman-Monteith法计算ET0——以太湖流域的应用为例[J].水资源保护,2010,26(1):6-8. [14] 刘战东,刘祖贵,秦安振,等.黄淮海地区基于温度的计算ET0方法比较及修正[J].节水灌溉,2014(4):1-6. [15] 赵 璐,梁 川,崔宁博,等.不同ET0计算方法在川中丘陵地区的比较及改进[J].农业工程学报,2012,28(24):92-97. [16] 王新华,郭美华,徐中民.分别利用Hargreaves和PM公式计算西北干旱区ET0的比较[J].农业工程学报,2006,22(10):21-25. [17] 张寄阳,孙景生,段爱旺,等.风沙区参考作物需水量计算模式的研究[J].干旱地区农业研究,2005,23(2):25-30.
