一种由序列图像重建皮肤表层形状的算法

徐连霞

(江苏财经职业技术学院,江苏 淮安 223003)

一种由序列图像重建皮肤表层形状的算法

徐连霞

(江苏财经职业技术学院,江苏 淮安 223003)

提出了一种从不同方向照射皮肤形成多幅图像重建皮肤表层的新方法。由于皮肤表层凹凸不平，而用传统的立体成像方法存在着镜面反射和全反射，不能精确地重建皮肤表层。而选取一些光强度数据，在这些数据中不包括镜面反射和全反射光强度数据，并从选取的数据中采用单值分解(SVD)方法可以精确计算出法向向量。实验结果表明，这种方法对在一系列包含镜面反射和全反射的序列图像中重建皮肤表层形状非常有效。

三维重建；镜面反射；自身阴影；皮肤表层

0 引言

由于皮肤表层的三维形状取决于皮肤的生理状况，精确的三维重建对于识别皮肤的质量和生理状况非常重要。皮肤每处的反射系数都是一致的，三维重建结果通常都能精确地反映出皮肤的形状。可是即使每一个物体的反射系数是均一的，也不能排除镜面反射。在图像成像中镜面反射、全反射时有发生[1-3]。利用传统的图像重建技术[4，5]实现三维重建是非常困难的。

为了克服这些问题，采用从不同方向光线照射来获取序列图像，可以获得足够反映反射系数的信息，与文献[6，7]研究相似。在这些研究方法中，通过多幅图像尽量恢复反射系数的参数，镜面反射的问题被解决了，然而全反射和自身阴影不容易解决，因为这些问题取决于物体形状本身。在文献[1，2]研究中提出综合分析结构来重建的方法。在这种方法中，图像先拼合成综合图像，然后用实际形椎分析合成的图像再与输入图像进行比较。虽然这种方法可以解决形状重建中的全反射和阴影问题，但是如果所采集的图像模糊，要精确重建还是比较困难的。

本文提出一种移动光源的方法，从获得的序列图像来重建皮肤表层，因为多幅图像能提供足够的信息来解决全反射、自身阴影及其它一些复杂的效应，能够识别图像进行精确的三维重建。在一个简单的模型下定义一个矩阵方程，在这模型中没有全反射和阴影等方面的影响。考虑到模型的误差，使用SVD(单值分解)的方法来解矩阵方程。在简单模型与实际情形之前产生了大量的误差，按照误差值选取误差样本计算差分。重复这个选项，选取服从这个简单模型的样本。利用这种方法，可以去除全反射和阴影，然后精确重建皮肤表层的三维形状。

为了验证方法的有效性，以下从一序列图像中展示了一些皮肤表层重建的情况。

1 图像校正排列

为了获取多方位的不同光源照射图像，使用图1的排列，三个光源之间的间隔为120°，每条光线都能旋转120°。

2 图像强度模型

在光源发射的假设下，一个远距离的单点光源，其在任意一点p(x,y)的强度可以用方程(1)来表示：

I=ηL·n

(1)

η是界面的反射系数，n是界面的法向量，L是光线的方向。如果能够得到在三个不同的光线方向L到一点的亮度I，可以利用反射系数η来重建在点p(x,y)的法向量[6]。如果拿三幅从不同的光源照射的图片，在每一个像素点方程(1)都满足，可以重建出每一像素点的表面法向量。然而由于镜面反射、全反射和自身阴影，大多数像素点还是不能够满足方程(1)。

为了克服这些问题，利用多条不同方向的光线L(θ)，光线在不同的角度θ下照射。然后方程(1)就可以写成如下的形式。

I(θ)=ηL(θ)·n

(2)

(3)

如果在光源照射方向每一条光线的值都满足方程(1),那么这值必须符合正弦曲线函数：

I(θ)=Asin(θ+B)+C

(4)

其中：

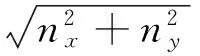
(5)

(6)

C=ηcosφnz

(7)

因此，可以在每一像素处通过I(θ)拟合正弦曲线来计算出表面法线。为了这个拟合，使用SVD方法来解矩阵方程。

(8)

其中光源的方向是表面的法向量角度分别为[θ1，θ2,…,θn]及固定夹角φ。

在实际情况中，I(θ)中只有部分的值满足方程(1)式。产生这种现象的原因是由表面存在着镜面反射及全反射以及阴影造成的。因此，必须提取出那些能够拟合正弦曲线强度的数据，以便能够精确计算出表面法向量(nx,ny,nz)，为了在模型中提取出强度数据，采用下面的处理步骤。

3 形状重建

3.1 算法流程图

算法的流程如图2所示。首先，校正光强度数据，因为三条光线的能量并不一样。其次，选择强度数据中不包括镜面反射和全反射以及自身阴影的数据。再次，再利用SVD方法按照方程(8)计算表面的法向量。最后，所有的法向量整合到一起得到皮肤表层的三维形状。

3.2 去除低强度数据

在图3中，显示的是在相差120°不同方向的光线在同一像素点的强度I(θ)。在图3(a)中的强度曲线，强度最小值基本上都是在200°～300°之间。在这些强度数据中有些值是不能低于某一固定值的，否则不能拟合出正弦曲线。

为了从拟合的正弦曲线中去除一些低强度的数据，设置一定的阈值，低于阈值的数据将被去除。阈值的取值靠最初的实验得出。

强度数据不能包括低值的数据是由于全反射的缘故。全反射把一些光的强度又反射到光源上去。图4是全反射效应的原理图。在区域A的表面，大部分全反射的光线来自区域B的表面。然而由于全反射的强度并不大，因为区域B表面的法线近似垂直光源的方向。相反，B区域表面的全反射强度非常的大，因为大部分全反射的光都是来自A区域表面，因为区域A表面的法线近似平行于光线的方向。按照这个全反射效应的经典模型，可以设想全反射大部分效应是低强度值数据，这就意味着在B表面反射强度非常小。

3.3 反复拟合亮度数据

即使在全面去除了低值强度数据以后，强度曲线也不能完全拟合正弦曲线。大部分是由于镜面反射和自身阴影造成的。

如果图像的强度数据Io(θ)和按照SVD方法由方程(8)计算出来的强度值Isvd(θ)差值远远大于阈值，那么图像的强度Io(θ)将被去除，因为这些值包括了镜面反射和自身阴影。在去除了这些数据之后，再开始利用SVD方法根据方程(8)进行计算。重复这个过程，当所有的剩余数据符合方程(1)朗伯模型的时候计算出表面法线。

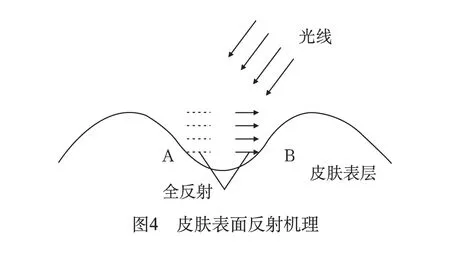
图3显示了去除数据的效应。通过在模型中选取数据，利用正弦曲线精确地拟合已提取出来的数据。相反，通过全部的曲线得到的正弦拟合曲线不能很好地匹配这些提取出来的强度数据。

3.4 整合

在通过选取数据后，按照方程(8)计算出表面的法向量(nx,ny,nz)，表面的梯度p(x,y),q(x,y)可以通过下面的方程计算出来：

(9)

(10)

再对这两个梯度进行积分可以得到皮肤表面的值z(x,y)：

(11)

4 实验

本方法已经应用到皮肤图像中。图像的大小是256×256。实际大小是4.5mm×4.5mm。输入图片在120°之间。

图5展示的是输入的是角度相差120°的皮肤表面图片。图6显示的是从图像系列中重建的皮肤形状俯视图。图7是所有输入图像的重建形状。之所以能够重建表皮形状是因为在重建范围内的图像二维结构与普通的图像几乎是一样的。

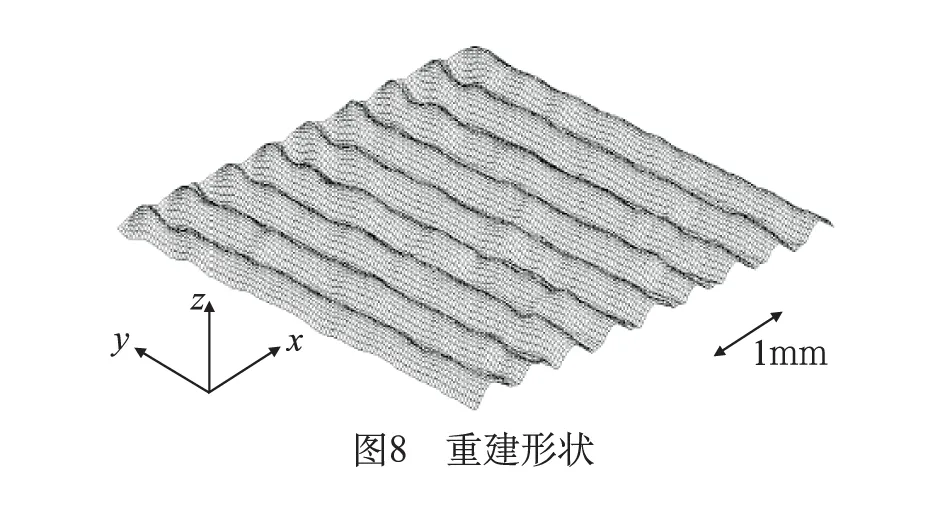
图8中展示了重建后的皮肤呈波浪状的形状。样品的横断面图像是通过对样品精确切割获得的，与图9中的侧面重建形状可以进行比较。利用本文的方法可以非常有效地重建出样品的形状。

5 结论

本文提出一种在不同方向光线照射下获取的序列图像中重建皮肤表面的新方法。在本文的方法中，抽取出模型的强度数据与正弦曲线的数据精确地拟合以求得表面的法向量。从图像的重建实验结果来看，本方法对于包括有镜面反射和全反射及自身阴影的图像有非常好的重建效果。

[1]LaurentiniA.Thevisualhullconceptforsilhouettebasedimageunderstanding[J].IEEETransonPatternAnalysisandMachineINtelligence,2010,16(2):150-162.

[2] 齐菲菲.基于多幅图像序列的三维重建算法的研究[D].天津：河北工业大学.2012.

[3]MartinWN,AggarwalJK.Volumetricdescriptionsofobjectsfrommultipleviews[J].IEEETransonPatternAnalysisandMachineIntelligence,2011,5(2)：150-158.

[4]K.IkeuchiB.K.P.Houn.Numericalshapefromshadingandoccludingboundaries[J].ArtificialIntelligence,2011,17(3):141-184.

[5] 祁长红.基于正交图像的头部三维模型构建[D].南京：东南大学.2015.

[6]PringleKK.Visualperceptionbyacomputer[A].InGrasselliAeditor.AutomaticInterpretationandClassificationofImages[C].NewYork:AcademicPress,2010:277-284.

[7]Y.Sato,K.Ikeuchi.Temporal-colorspaceanalysisofreflectionProcIEEE[J].ComputerVisionandPatternRecognition,2013,9(1):570-576.

3D Reconstruction of Skin Surface from Image Sequence

XULian-xia

(JiangsuVocationalCollegeofFinanceandEconomics，Huai’an223003，China)

This paper proposes a new method for reconstructing a shape of skin surface replica from shading image sequence taken with different light source directions. Since the shading images include shadows caused by surface height fluctuation, and specular and inter reflections, the conventional photometric stereo method is not suitable for reconstructing its surface accurately. In the proposed method, we choose intensity data which do not include specular and inter reflections and self-shadows so that we can calculate accurate normal vector from the selected intensity data using SVD (Singular Value Decomposition) method. The experimental results from real images demonstrate that proposed method is effective for shape reconstruction from shading images which include specular and inter reflections and self-shadows.

3D reconstruction; specular reflection; self-shadow; skin surface

2017-01-02

淮安市科技支撑计划(HAS2014023-3)

徐连霞(1980-)，女，硕士研究生，江苏财经职业技术学院工程学院讲师，研究方向：图像处理、计算机技术应用。

TP391

A

1674-3229(2017)01-0030-04