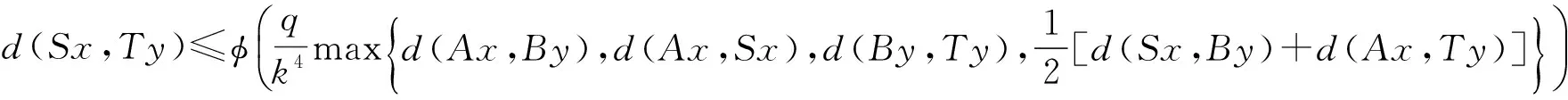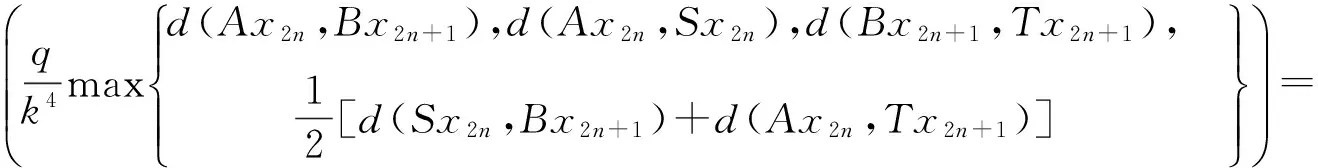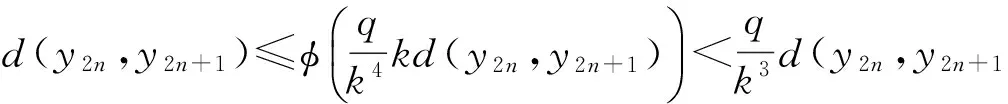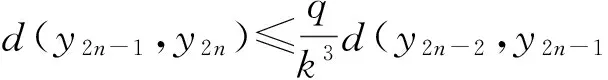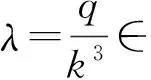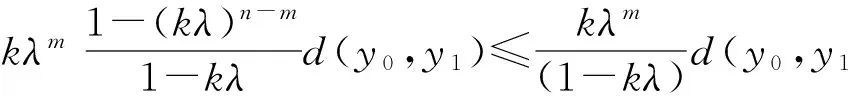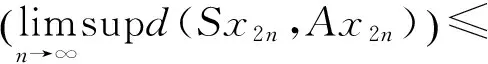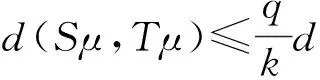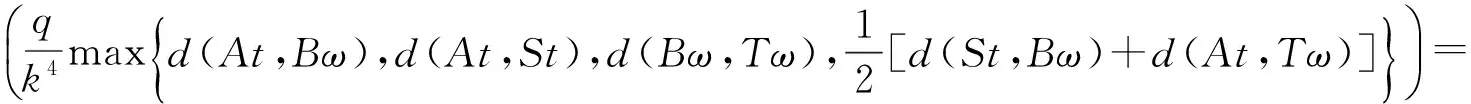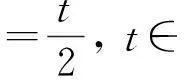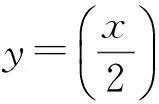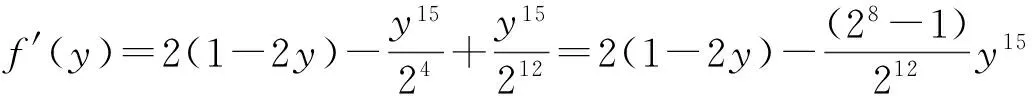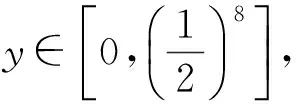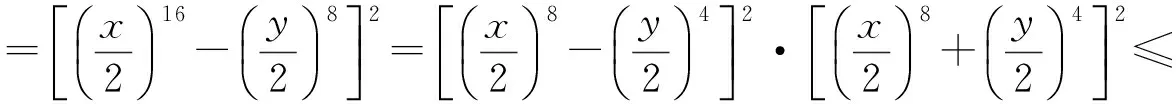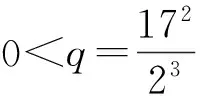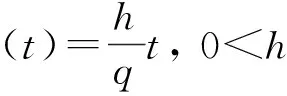b-度量空间中φ-弱交换映像的公共不动点定理

姜 云，谷 峰

(杭州师范大学应用数学研究所, 杭州师范大学理学院,浙江 杭州 310036)

b-度量空间中φ-弱交换映像的公共不动点定理

姜 云，谷 峰

(杭州师范大学应用数学研究所, 杭州师范大学理学院,浙江 杭州 310036)

在完备b-度量空间的框架下，利用自映像对φ-弱交换的条件， 讨论了一类新的压缩型映像公共不动点的存在性和唯一性问题，获得了一个新的公共不动点定理， 所得结果是b-度量空间中公共不动点理论的进一步发展和完善.

b-度量空间;φ-弱交换映像; 公共不动点

1 引言和预备知识

在介绍主要结果之前，先介绍一些基本概念和已知结果.

定义1[1]设X是一非空集,k≥1是一给定的实数, 称函数d:X×X→[0,∞) 是集合X上的一个b-度量，若对任意的x,y,z∈X, 有以下条件满足：1)d(x,y)=0当且仅当x=y; 2)d(x,y)=d(y,x); 3)d(x,y)≤k[d(x,z)+d(z,y)].

这时称(X,d)是X上的一个b-度量空间，实数k≥1称为该b-度量空间的系数.

注1[2]当k=1时，b-度量空间即为通常的度量空间，但一般情况下,b-度量空间未必是度量空间，例子可见文献[2]中例3.1.

注2[3]集合X上的一个b-度量不一定连续，例子可见文献[3]中例1.3.

定义3[4]设(X,d)为b-度量空间, {xn}是X中的序列, 如果存在x∈X, 使得

命题1[4]每个b-收敛点列的极限都是唯一的，而且每个b-收敛点列都是b-Cauchy列.

定义4[4]设(X,d)是b-度量空间，如果X中的每个b-Cauchy列都在X中b-收敛，则称b-度量空间(X,d)是b-完备的.

定义5[10]b-度量空间(X,d)上的自映像S和T是称为是弱交换的，如果∀x∈X，有

d(STx,TSx)≤d(Sx,Tx).

定义6[11]b-度量空间(X,d)上的自映像S和T称为是R-弱交换的，如果存在实数R>0, 使得对于任意的x∈X，有

d(STx,TSx)≤Rd(Sx,Tx).

定义7[12]b-度量空间(X,d)上的自映像S和T称为是φ-弱交换的(也称广义拟弱交换的)，如果存在φ:[0,∞)→[0,∞), 在[0,∞)上连续且φ(0)=0, 使得∀x∈X有d(STx,TSx)≤φ(d(Sx,Tx)).

引理1[13]设(X,d)是一个b-度量空间，其系数k≥1. 设{xn}和{yn}是X中的两个b-收敛列，分别收敛于x和y，则有

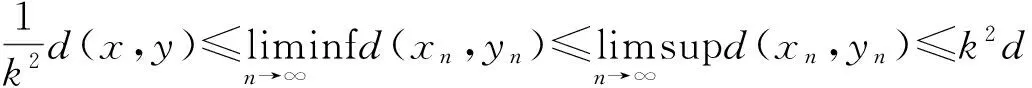
注3[12]显然，弱交换映像必是R-弱交换映像，R-弱交换映像也必是φ-弱交换映像，但反之不真.

例1 设X=[0,+∞), 定义d(x,y)=(x-y)2, 则(X,d)是一个b-度量空间，设Tx=x2,Sx=3x2, 则存在φ(t)=3t2, 使∀x∈X，有

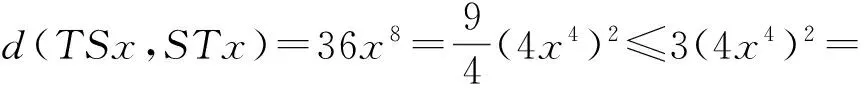
d(TSx,STx)=36x8=9x4·4x4=9x4·d(Tx,Sx)>ad(Tx,Sx).

故T和S不是弱交换的.

2 主要结果

定理1 设(X,d)是具有系数k≥1的完备b-度量空间，(S,A)和(T,B)是X上两对连续的φ-弱交换映像，如果存在从[0,∞)到自身的递增函数φ满足φ(t)=t当且仅当t=0, 且0<φ(t)0, 且以下条件成立：

(1) 存在点列{xn},{yn}⊂X,满足

y2n+1=Tx2n+1=Ax2n+2,y2n=Sx2n=Bx2n+1,yn≠yn+1,∀n∈Z+.

(1)

(2) 存在0

(2)

则序列{Syn}收敛于S,T,A和B在X中的唯一公共不动点.

证明 由条件(1)和(2)得

如果d(y2n,y2n+1)>d(y2n-1,y2n), 由上式可得

(3)

矛盾，故必有d(y2n,y2n+1)≤d(y2n-1,y2n),因此

(4)

使用(1)和(2)同理可得

(5)

组合(4)和(5)得

d(yn,yn+1)≤λd(yn-1,yn)∀n∈Z+.

(6)

d(yn,yn+1)≤λd(yn-1,yn)≤…≤λnd(y0,y1).

(7)

对于所有的n>m, 使用三角不等式和式(7)可得

因为λ∈(0,1), 所以当n,m→∞时, 由上式可得d(yn,ym)→0, 因此{yn}是一个Canchy列. 由X的完备性知存在μ∈x, 使得yn→μ(n→∞),从而有

(8)

由于(S,A)是φ-弱交换映像，故有d(SAx2n,ASx2n)≤φ(d(Sx2n,Ax2n)). 于是由S,A和φ的连续性，使用引理1得

故得Sμ=Aμ, 同理可得Tμ=Bμ. 下证Sμ=Tμ, 否则，使用条件(1)可得

d(St,At)=d(SAμ,ASμ)≤φ(d(Sμ,Aμ))=φ(d(t,t))=φ(0)=0

从而St=At,同理可证Tt=Bt, 于是SAμ=ASμ,TBμ=BTμ. 如果d(St,t)≠0, 则由条件(2)得

下证公共不动点的唯一性. 事实上, 假设ω∈X也是是S,T,A,B的一个公共不动点且ω≠t, 则由条件(2)可得

例2 令X=[0,1], 定义b-度量d(x,y)=(x-y)2, ∀x,y∈X. 则(X,d)是系数k=2的完备b-度量空间. 定义A,B,S和T如下：

(9)

要证d(SAx,ASx)≤φ(d(Sx,Ax)). 即

[1] CZERWIK S. Contraction mappings inb-metric spaces[J]. Acta Math Inf Univ Ostrav,1993,1(1):5-11.

[2] AKKOUCHI M. A common fixed point theorems for expansive mappings under strict implicit conditions on-metric spaces[J]. Acta Univ Palack Olomuc Fac Rerum Natur Math,2011,50(1):5-15.

[3] LATIF A, PARVANEH V, SALIMI P, et al. Various Suzuki type theorems inb-metric spaces[J]. J Nonlinear Sci Appl,2015,8:363-377.

[4] BORICEANU M. Strict fixed point theorems for multivalued operators inb-metric spaces[J]. Int J Mod Math,2009,4(3):285-301.

[5] ROSHAN J R, SHOBOLAEI N, SALEDGHI S, et al. Common fixed point of four maps in-metric spaces[J]. Hacettepe Journal of Mathematics and Statistics,2014,43(4):613-624.

[6] AGHAJANI A, ABBAS M, ROSHAN J R. Common fixed point of generalized weak contractive mappings in partially orderedb-metric spaces[J]. Math Slovaca,2014,64(4):941-960.

[7] 董清平,谷峰.广义拟弱交换映象的公共不动点定理[J].杭州师范学院学报(自然科学版),2008,7(1):21-23.

[8] 巨小维,谷峰.一类压缩映像的公共不动点定理[J].杭州师范学院学报(自然科学版),2006,5(5):382-386.

[9] 陈军民,谷峰.一类新的φ-压缩映像的公共不动点定理[J].杭州师范学院学报(自然科学版),2007,6(6):414-418.

[10] SESSA S.On a weak communitivity condition of mappings in fixed point consiiderations[J].Pub Inst Math,1982,32(46):149-153.

[11] PANT R P.Common fixed points of noncommuting mapping[J].J Math Anal,1994,188(2):436-440.

[12] 张树义.Altman型映射的公共不动点定理[J].烟台师范学院学报(自然科学版),2000,16(2):95-97.

[13] AGHAJANI A， ABBAS M， ROSHAN J R. Common fixed point of generalized weak contractive mappings in partially orderedb-metric spaces,[J].Math Slovaca,2014,64(4):941-960.

Common Fixed Point Theorem ofφ-weak Commuting Mappings inb-metric Spaces

JIANG Yun, GU Feng

(Institute of Applied Mathematics, School of Science, Hangzhou Normal University, Hangzhou 310036, China)

In the framework of completeb-metric space, by using theφ-weak commuting condition of self-mapping pairs, the existence and uniqueness of common fixed point for a class of new contractive mappings was discussed. A new common fixed point theorem is obtained. The result further developed and improved the common fixed point theories inb-metric space.

b-metric space;φ-weak commuting mappings; common fixed point

国家自然科学基金项目(11071169);浙江省自然科学基金项目(Y6110287).

谷峰(1960—),男,教授,主要从事非线性泛函分析及应用研究. E-mail：gufeng99@sohu.com

10.3969/j.issn.1674-232X.2017.02.011

O177，O189 MSC2010：47H10,54H25,55M20

A

1674-232X(2017)02-0181-06