基于气候要素的凤阳县小型蒸发皿蒸发量估算

2017-04-11袁学所夏志芬葛庆云王刚王楠楠郭

安徽农学通报 2017年6期

袁学所+夏志芬+葛庆云+王刚+王楠楠+郭阳+周礼清

摘要：该文基于凤阳国家气象观测站1980—2013年气象观测资料，运用SPSS软件，研究全年各月20cm口径小型蒸发皿蒸发量与相关气候要素的相关关系，建立逐步回归模型。结果表明，相对湿度、日照时数、地表温度等要素对蒸发量年际变化影响显著，回归方程复相关系数大部分大于0.900。在此基础上建立了年蒸发量回归模型，月蒸发估值年合计、年降水量被引入方程，其复相关系数0.810。研究结果便于地面气象观测业务调整后月（年）蒸发量的估算和续补，可以为农业和生态气象服务提供依据。

关键词：气候要素；小型蒸发皿；蒸发量；逐步回归；资料续补；SPSS软件

中图分类号 S161.4 文献标识码 A 文章编号 1007-7731（2017）06-0170-04

Calculations of Small Evaporation Capacity Based on the Climate Elements in Fengyang

Yuan Xuesuo et al.

（Fengyang County Bureau of Meteorology，Fengyang 233100，China）

Abstract：Based on Fengyang national meteorological observatory meteorological observation data from 1980 to 2013，using SPSS software，the whole year months 20 cm diameter small-sized evaporation pan evaporation and related to the correlation between climate and stepwise regression model is established.Results indicate that the relative humidity，sunshine time，the surface temperature and other factors impact on evaporation interannual change significantly，the regression equation of most of the multiple correlation coefficient is greater than 0.900.Based on the regression model，annual evaporation on evaporation valuations in total，annual precipitation was introduced into equation of the multiple correlation coefficient of 0.810.The results for the ground meteorological observation business adjustment after month （year） evaporation capacity estimation and renewal，can provide the basis for agriculture and ecological meteorological service.

Key words：Climate；Small evaporating dish；Evaporation；Stepwise regression；The data renewal；SPSS software

1 引言

蒸发皿蒸发量是估计土壤蒸发和农业水资源管理的重要指标，是大气蒸发能力的综合体现[1]。根据中国气象局综合观测司关于做好全国地面气象观测业务调整工作的通知（气测函〔2013〕321号），自2014年1月1日起，国家一般气象站取消小型蒸发观测。为满足气象服务需求，需借助相关气候要素对蒸发量进行定量估算。在全球气候变化背景下，特定区域一定时期蒸发量的变化趋势及成因研究多有报道[2-15]，例如，陈伯龙等开展了20cm口径蒸发皿蒸发量的数学物理模型研究[16]，王明星就干旱区气象因子对蒸发皿蒸发量影响做了观测及数值模拟[17]。上述研究有利于揭示蒸发的物理过程和时空演变规律，但不是针对部分气象台站蒸发量停测后的资料续补。本研究旨在探讨一种基于单站气候要素的月（年）蒸发量简便实用估算方法，为蒸发量停测后开展农业和生态气象服务提供依据。

2 资料与方法

本文选取凤阳国家气象观测站1980—2013年气象观测资料，运用SPSS软件[18]中相关分析、逐步回归等数理统计方法，研究全年各月小型蒸发的年际变化与同期气温、日照时数、降水量、降水日数、地表温度、风速、湿度等气候要素的相关关系，建立逐步回归统计模型。这些气候要素涉及影响蒸发的热力、动力、水分三類因子[17]，具有较好的代表性，并容易取得。在此基础上，对年蒸发量进行统计建模。各要素采集方法：蒸发取20cm口径小型蒸发皿观测值（mm），气温取月（年）平均气温（℃），日照时数取月（年）日照时数合计值（h），降水量取月（年）降水量合计值（mm），地表温度取月（年）0cm平均地温（℃），风速取月（年）2min平均风速（m/s），湿度取月（年）平均相对湿度（%）。

3 结果与分析

3.1 月蒸发量与气候要素相关分析以凤阳11月气象资料为例，描述了该月蒸发量与同期日照时数、湿度的对应关系，见图1。从图1可以看出：随着日照时数的增多，蒸发量随之增大；随着湿度的增大，蒸发量随之减小。表明蒸发量与日照时数、湿度分别存在正相关和负相关关系。以此类推，其他月份蒸发量与气候要素也存在明显相关关系，其定量化分析结果可通过SPSS软件统计得到。

[250

200

150

100

0][11月湿度（%）和日照时数（h）][30][50][70][90][110][130][11月烝发量（mm）][◆湿度 ■日照时数]

图1 凤阳11月蒸发量与同期湿度、日照时数对应关系

（1980—2013年）

表1列出凤阳各月蒸发量与同期气候要素相关系数。其信度0.05和0.01显著性水平的相关系数标准分别为0.339和0.436。由此可知，凤阳各月蒸发量与同期气候要素相关显著，其中气温基本都是正相关，2、3、5—8月达显著以上标准，达极显著标准有5个月，最大相关系数0.802（8月），表明气温升高对应蒸发量增加；日照时数全部正相关，12个月均达极显著水平，最大相关系数0.848（5月），表明日照时数增多与蒸发量增加对应关系极好；降水量全部是负相关，12个月均达极显著水平，绝对值最大相关系数-0.775（3月），表明降水量增多与蒸发量减小对应关系极好；降水日数全部是负相关，12个月均达极显著水平，绝对值最大相关系数-0.811（11月），表明降水日数增多与蒸发量减小对应关系极好；地表温度基本都是正相关，2—10月达显著以上标准，达极显著标准有8个月，最大相关系数0.909（8月），表明地表温度升高对应蒸发量增加；风速有8个月负相关，4个月正相关，其中11月相关系数-0.418，达显著水平。因此在多种因子综合作用下，风速大蒸发量不一定就大，因风速较大时可能热力或水分因子配置不利而影响蒸发，这和具体天气条件有关；湿度全部负相关，12个月均达极显著水平，绝对值最大相关系数-0.883（11月），表明湿度增大与蒸发量减小对应关系极好。

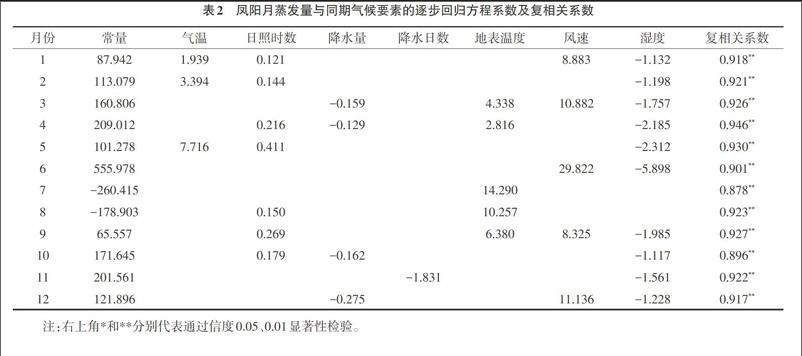
3.2 月蒸发量逐步回归模拟表2给出凤阳各月蒸发量与气候要素的逐步回归方程系数及复相关系数。由表2可见，全年12个月中，有4个月入选因子数为4个（1、3、4、9月），4个月入选因子数3个（2、5、10、12月），3个月入选因子数2个（6、8、11月），1个月入选因子数1个（7月）。12个月中，各因子被引入方程的次数依次为：湿度10次、日照时数7次、地表温度5次、风速5次、降水量4次、气温3次、降水日数1次。回归方程复相关系数在0.900以上的10个，最高0.946（4月）；最低复相关系数0.878（7月）。各回归方程复相关系数经检验均达极显著水平，可以用来对月蒸发量进行估算和续补。

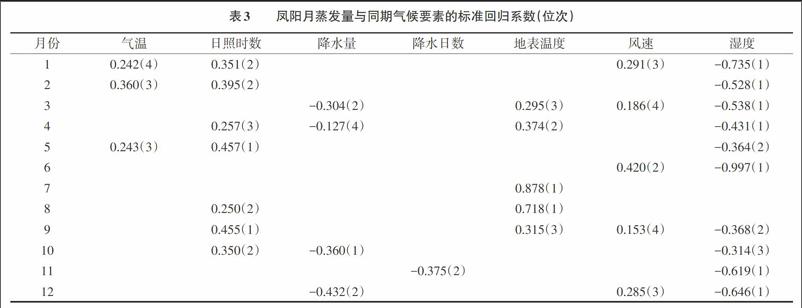
表3给出了凤阳月蒸发量与同期气候要素的标准回归系数。标准回归系数消除了因子量纲的对系数大小的影响，可以用来比较各因子对回归方程贡献的大小。例如，1月主导因子排序为湿度、日照时数、风速、气温；2月为湿度、日照时数、气温；3月为湿度、降水量、地表温度、风速等，以此类推。比较表1可以看出，相关系数最大的，标准回归系数通常也最大，但也有例外。例如，2月日照时数相关系数优于湿度，但标准回归系数相对较小。该回归方程还引入了第3個因子即气温，在3个因子组合条件下，日照时数对回归方程的贡献被重新定位，湿度因子的作用得到提升。从表3可见，湿度第1排序7次，第2排序2次；日照时数第1排序2次，第2排序4次；地表温度第1排序2次，第2排序1次；降水量第1排序1次，第2排序2次；风速无第1排序，第2排序1次；降水日数无第1排序，第2次排序1次，气温无第1第2排序。因此，从标准回归系数位次情况看，表现前3名的因子为湿度、日照时数、地表温度。包括出现负相关情况的风速在内，所有入选因子的回归系数符号均符合物理规律。

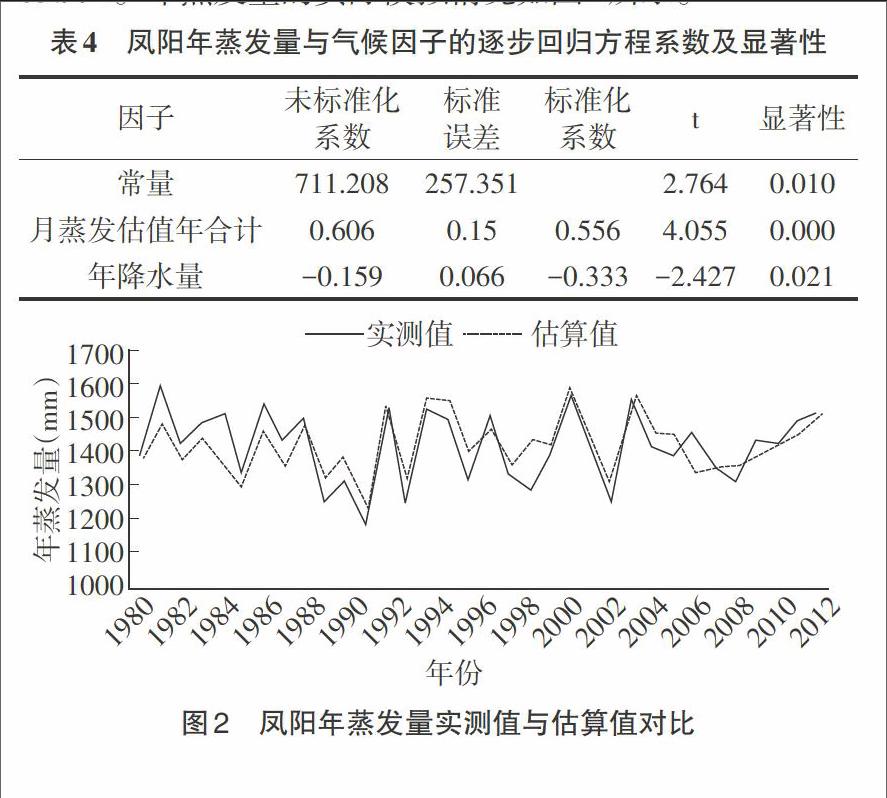
3.3 年蒸发量逐步回归模拟在月蒸发量估算的基础上，虽然可以将各月蒸发量相加（月蒸发估值年合计）得到年蒸发量的估算值，但考虑到回归统计值本身是近似值，近似值多次相加可能会造成误差的积累，所以直接用年蒸发量与相关气候要素建立逐步回归统计模型。待选因子包括湿度、日照时数、地表温度、风速、降水量、气温、降水日数的年度值和月度值91个，同时加上月蒸发估值年合计，经相关分析初选后，挑选影响较显著的因子统计建模。最终入选因子情况如表4所列，即月蒸发估值年合计、年降水量入选回归方程，它们与年实际蒸发量的相关系数分别为0.769、-0.688，回归方程复相关系数0.810，标准差63.994。年蒸发量的实际模拟情况如图2所示。

4 结论与讨论

（1）凤阳各月气温、日照时数、降水量、降水日数、地表温度、湿度与月蒸发量大部分存在显著或极显著相关关系，各因子相关系数绝对值最大的分别为0.802（8月）、0.848（5月）、-0.775（3月）、-0.811（11月）、0.909（8月）、

-0.883（11月）；风速与蒸发量的单相关多不显著，说明风速不是造成凤阳蒸发量年际变化的主导因子。

（2）运用逐步回归方法建立各月蒸发量的估算模型，复相关系数在0.900以上的10个，最高为0.946。从入选因子数量看，从大到小排序为湿度、日照时数、地表温度、风速、降水量、气温、降水日数；从入选因子标准回归系数排位看，依次为相对湿度、日照时数、地表温度、降水量、风速、降水日数、气温。无论是因子数量和主次排位，前3位因子均为湿度、日照时数、地表温度。

（3）单用月蒸发估值年合计来估算年蒸发量，其相关系数0.769，扩充91个备选因子后进行逐步回归分析，月蒸发估值年合计、年降水量被引入方程，其复相关系数提高到0.810。年蒸发量的模拟效果不如月蒸发量，是否有更好的因子有待进一步探索。

（4）本文尝试用气候要素估算凤阳月（年）小型蒸发量，回归统计效果极显著，物理意义确切，对其他有同类需求的观测站有参考价值。

参考文献

[1]Stanhill G.Is the Class A evaporation pan still the most practical and accurate meteorological method for determining irrigation water requirements？[J].Agricultural and Forest Meteorology，2002，112（34）：233-236.

[2]Roderick M L，Farquar G D.The cause of decreased pan evaporation over the past 50 years[J].Science，2002，298：1410-1411.

[3]Brutsaert W，Parlange M B.Hydrological cycle explain the evaporation paradox[J].Nature，1998，396：30-31.

[4]Rayner D P.Wind run changes：The dominant factor affecting pan evaporation trends in Australia[J].J Climate，2007，20：3379-3394.

[5]Peterson T C，Golubev V S，Groisman P Y.Evaporation losing its strength[J].Nature，1995，377：687-688.

[6]刘敏，沈彦俊，曾燕，等.近50年中国蒸发皿蒸发量变化趋势及原因[J].地理学报，2009，64（3）：259-269.

[7]左洪超，鲍艳，张存杰，等.蒸发皿蒸发量的物理意义、近40年变化趋势的分析和数值实验研究[J].地球物理学报，2006，49（3）：680-688.

[8]左洪超，李栋梁，胡隐樵.近四十年中国气候变化趋势及其同蒸发皿观测的蒸发量变化的关系[J].科学通报，2005，50（11）：125-1130.

[9]劉波，马柱国，丁裕国.中国北方近45年蒸发变化的特征及与环境的关系[J].高原气象，2006，25（5）：840-848.

[10]邱新法，刘昌明，曾燕.黄河流域近四十五年蒸发皿蒸发量的气候变化特征[J].自然资源学报，2003，18（4）：437-442.

[11]曾燕，邱新法，刘昌明，等.1960-2000年中国蒸发皿蒸发量的气候变化特征[J].水科学进展，2007，18（3）：311-318.

[12]郭军，任国玉.黄淮海流域蒸发量的变化及其原因分析[J].水科学进展，2005，16（5）：666-672.

[13]范伶俐.广东区域气象水文环境下蒸发皿蒸发量变化研究[D].南京：南京信息工程大学，2011.