海上柔性并联平台空间动力学建模与分析

谢克峰， 张合， 刘善增， 李豪杰

(1.南京理工大学 智能弹药技术国防重点学科实验室， 江苏 南京 210094；2.中国矿业大学 机电工程学院， 江苏 徐州 221116)

海上柔性并联平台空间动力学建模与分析

谢克峰1， 张合1， 刘善增2， 李豪杰1

(1.南京理工大学 智能弹药技术国防重点学科实验室， 江苏 南京 210094；2.中国矿业大学 机电工程学院， 江苏 徐州 221116)

针对某海上螺旋副- 虎克铰- 球铰(HUS)柔性并联平台由快速稳定和大负载引起的支撑连杆弹性变形和负载瞄准位置偏差问题，进行了空间弹性动力学建模。采用模态函数和空间等截面梁单元模型对弹性连杆进行空间建模，基于虎克铰和球铰连接的连杆为两自由度空间运动，推导了空间单元坐标与系统坐标的两自由度转换矩阵，利用平台的运动学和动力学约束条件建立了HUS柔性并联平台的空间弹性动力学方程；运用Newmark方法对弹性动力学方程进行离散求解，分析了平台的弹性动力学响应和支撑连杆的最大动应力，并进行了动力学测试实验；进一步分析了弹性变形对负载瞄准精度的影响。研究结果表明：由弹性变形引起的支撑点最大位移为2.45 mm，且x轴明显大于y轴和z轴；由弹性角位移引起最大位置偏差为1.35 m. 实验结果与仿真结果一致，验证了数值建模的有效性。

机械学； 柔性并联机构； 空间动力学建模； 弹性变形； 弹性连杆

0 引言

海上平台从尺寸上可以分为大型平台和小型平台，常见的大型平台有石油钻井平台、风电设备平台等[1-2]。小型平台有水面舰艇平台、舰载平台和海上漂浮并联平台等[3-5]，小型的海上漂浮并联平台可以灵活投放，并且快速稳定，能够实现一定范围海上防御、信息预警，当前我国潜艇在自我防御和逃生方面缺少必要手段，因此对于潜艇的自我防御，小型海上平台的研究具有重要意义。海上漂浮并联平台由于受到波浪和强流的干扰，会产生一定幅度的姿态偏转，为稳定负载设备，海上平台必须具有一定的快速稳定能力，同时由于海上平台主要的负载设备如探测设备、跟踪设备和防御设备等，都具有较大的质量和惯量。因此在海上平台调平稳定过程中支撑连杆会产生一定的弹性变形，从而对平台的稳定精度和负载的跟踪精度产生一定的影响，故在系统分析的过程中考虑由构件变形引起的位移误差成为并联平台高精度控制的关键[6-7]。国内外学者在并联机构动力学方面进行了一些研究分析，考虑构件弹性影响日益成为具有大负载的并联平台研究领域的新课题[8-10]。文献[11-12]主要对海上漂浮并联平台进行了刚体动力学分析，着重分析了刚性系统的运动规律。落海伟等[13]、Wang等[14]、张清华等[15]建立了柔性杆件的平面3自由度移动副- 转动副- 转动副/移动副- 转动副- 球面副(3-PRR/PRS)等并联机构的动力学模型，分析了动平台的响应和连杆末端的振动。Piras等[16]、刘善增等[17]利用有限元理论和弹性动力学性能分析方法建立了3自由度转动副- 转动副- 球面副(3-RRS)柔性并联机器人的动力学模型，分析了系统的弹性位移误差和固有频率等问题。但是上述弹性动力学分析均着重在平面运动副内进行，而海上漂浮螺旋副- 虎克铰- 球铰(HUS)柔性并联平台的弹性连杆通过虎克铰和球铰与动平台连接，在系统运动过程中为二自由度的空间运动，需要对此进行空间三维建模和分析。

本文针对海上漂浮HUS柔性并联平台的运动特点，分析由连杆机构引起的弹性形变，基于空间等截面梁单元模型描述连杆模型，运用Lagrange方程和虚功原理建立了空间的弹性动力学模型，并对系统的弹性运动位移和负载的瞄准位置误差进行分析。

1 海上HUS并联平台坐标系建立

柔性并联平台通过支撑连杆调节平台平衡，系统的刚性运动耦合了支撑连杆的弹性变形，形成刚柔耦合多体系统，产生非线性动力学响应。考虑微小弹性运动的影响，运用弹性力学和分析力学的分析方法，采用Lagrange方程和虚功原理建立海上HUS柔性并联平台的空间弹性动力学模型。

图1为并联平台的机构简图，并联平台为空间两自由度稳定平台，由两个驱动支链(HUS支链CiBiAi)和动平台PA1A2构成。支链采用滚珠丝杆驱动，由一个螺旋副、一个虎克铰和一个球面副组成，且球面副的中心A1、A2位于动平台。动平台是以P点为中心的圆柱体，分别通过A1、A2和P连接传动支链和基座，并且A1、A2和P的连线构成等腰直角三角形。

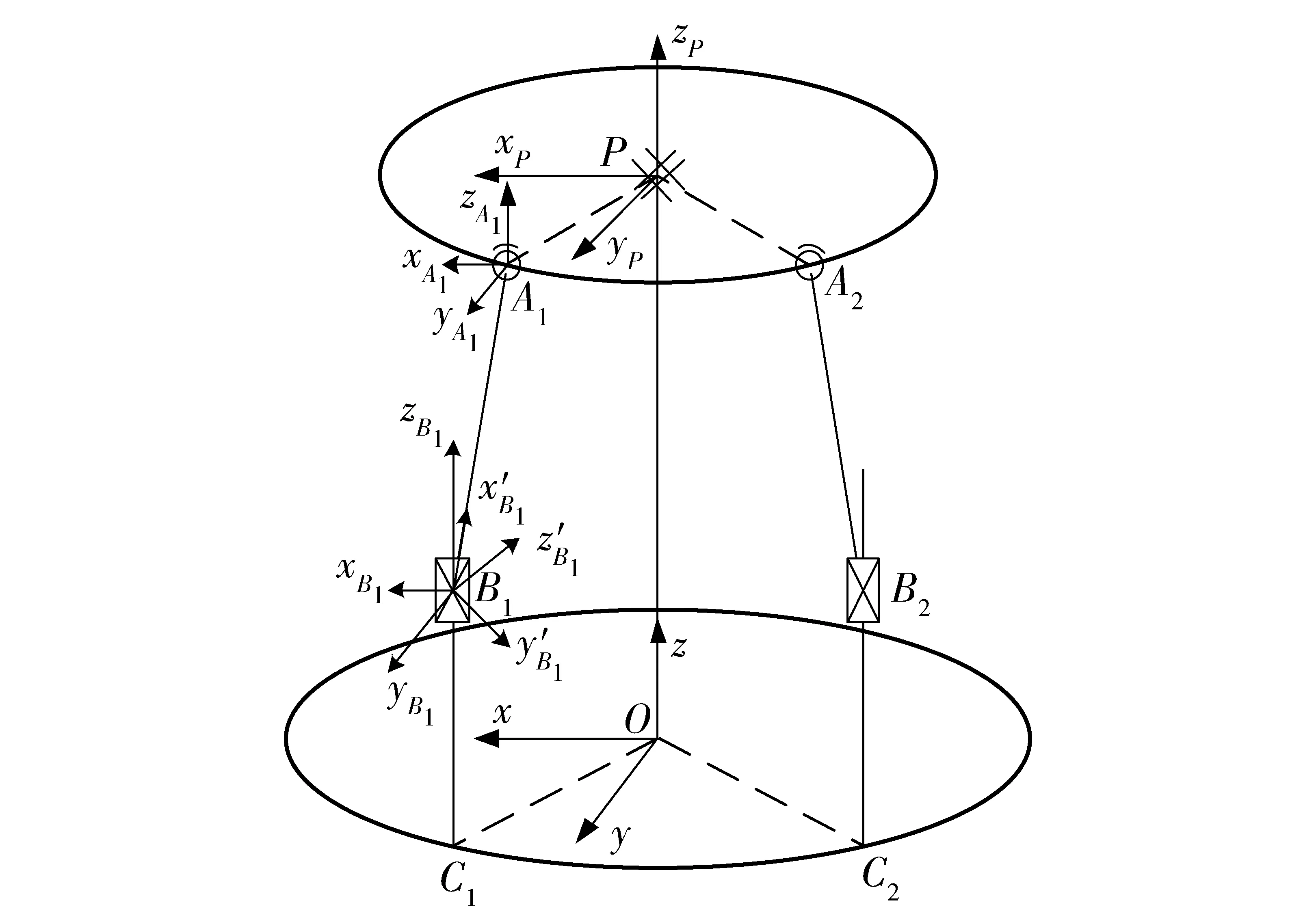
图1 海上漂浮HUS柔性并联平台机构简图Fig.1 Mechanism sketch of HUS flexible parallel platform

在基座O点建立总体坐标系Oxyz，y轴为两支链在基座投影的角平分线方向，z轴垂直向上，x轴按照右手坐标系建立。在动平台虎克铰处建立动平台固连坐标系PxPyPzP，其坐标轴静止时与系统总体坐标系对应，u0=[βγ]T为两自由度动平台的广义坐标。在虎克铰B1处建立平动坐标系B1xB1yB1zB1，其坐标轴静止时与系统总体坐标系对应。在虎克铰B1处建立转换坐标系B1x′B1y′B1z′B1，其x′B1轴与平动坐标系B1xB1yB1zB1的zB1轴一致，其z′B1轴与半径OC1平行，指向O点，y轴由右手坐标系确定。在虎克铰B1处建立连体坐标系B1x″B1y″B1z″B1，其x″B1轴从连杆B1点指向A1点，y″B1轴和z″B1轴分别在连杆横截面内，满足右手定则。

2 海上HUS柔性并联平台空间动力学建模

2.1 HUS柔性并联平台的弹性连杆空间建模

球铰Ai由于两自由度动平台的约束作用而具有空间3个方向的位移，因此连杆AiBi的运动为空间运动。螺帽Bi与连杆AiBi之间为虎克铰连接，因此在转换坐标系B1x′B1y′B1z′B1中，连杆AiBi为空间两自由度转动。

弹性杆建模选用空间等截面梁单元模型，如图2所示，在建模过程中忽略了关节摩擦和构件扭转变形的影响。节点分别用A3、B3来表示，建立单元坐标系B3xB3yB3zB3如图2所示，xB3方向为单元轴向，从B3指向A3，yB3、zB3分别在单元横截面内，构成右手直角坐标系，空间等截面两单元模型为圆柱体。梁单元广义坐标用δ表示，δ=[δ1δ2…δ17δ18]T，分别表示两个单元节点的弹性位移、角位移和曲率。则梁单元上任意一点的横向弹性位移、轴向弹性位移以及弹性角位移均可以表示为广义坐标的函数：

式中：N1、N2、N3为插值向量，采用梁单元节点的边界条件，可以求出插值向量的各型函数。

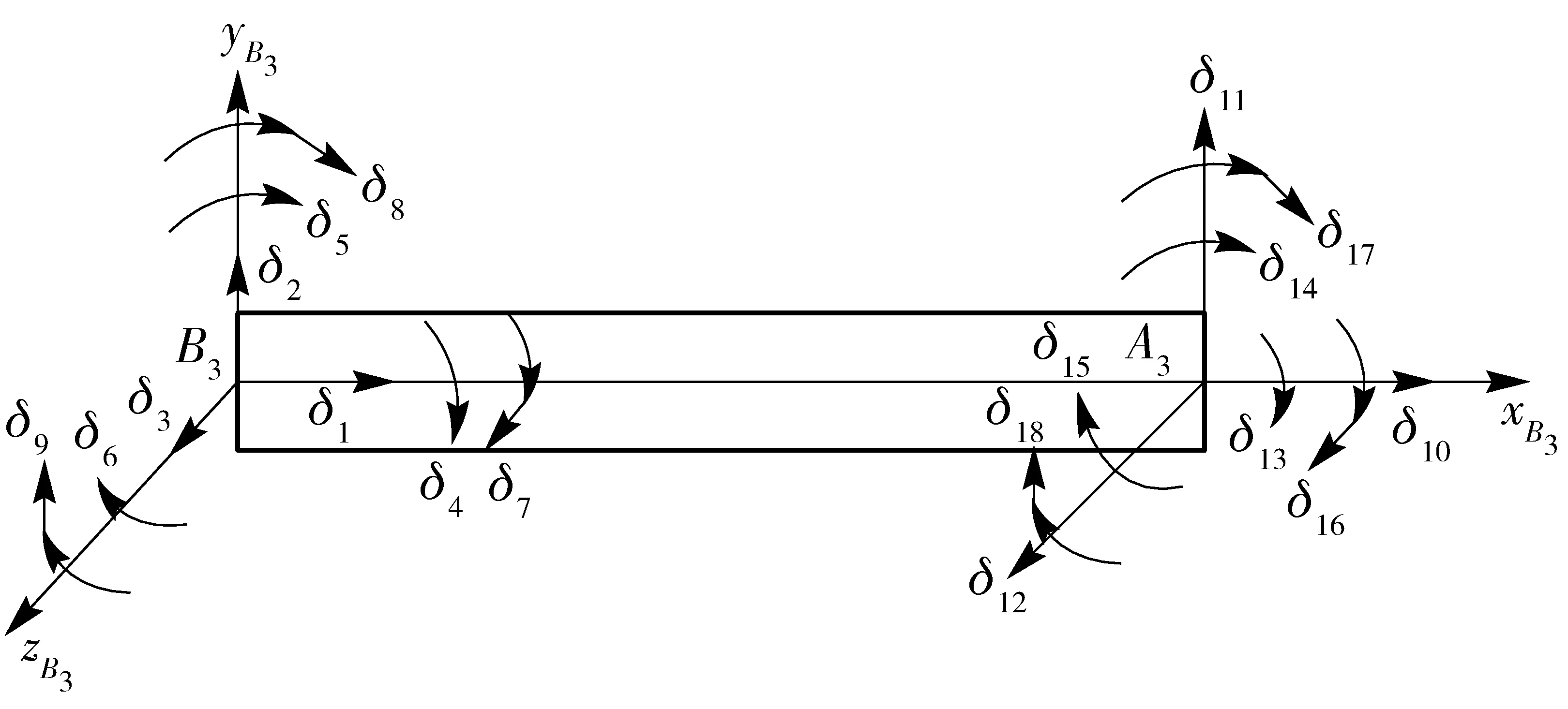
图2 空间等截面梁单元模型Fig.2 Space uniform section beam element model

以节点处的广义坐标作为未知量，对梁单元上的位移分布和角位移分布进行假定，横向位移假设为5次艾尔米特差值，轴向位移假设为线性差值，绕x轴的弹性角位移假设为3次差值。HUS柔性并联平台的定平台和动平台基座刚度较大；滚珠丝杆两端固定，其横截面积是支链连杆的两倍左右；支链连杆在整个系统中的长径比最大，因此支链连杆是系统中刚性最差的位置。由于HUS柔性并联平台的大负载和高惯量，在系统加速度剧烈的时刻，系统中表现出柔性的位置最可能出现在支链连杆处。本文选择两支链连杆为弹性杆，分别将连杆A1B1、A2B2设为一个梁单元(梁单元的个数根据仿真结果和并联平台要求进行调整)，如图3(a)所示，图中i=1,2. 因此，杆件AiBi的广义坐标为13个，即

δ=[δ1…δ700δ8…δ13000]T.

(1)

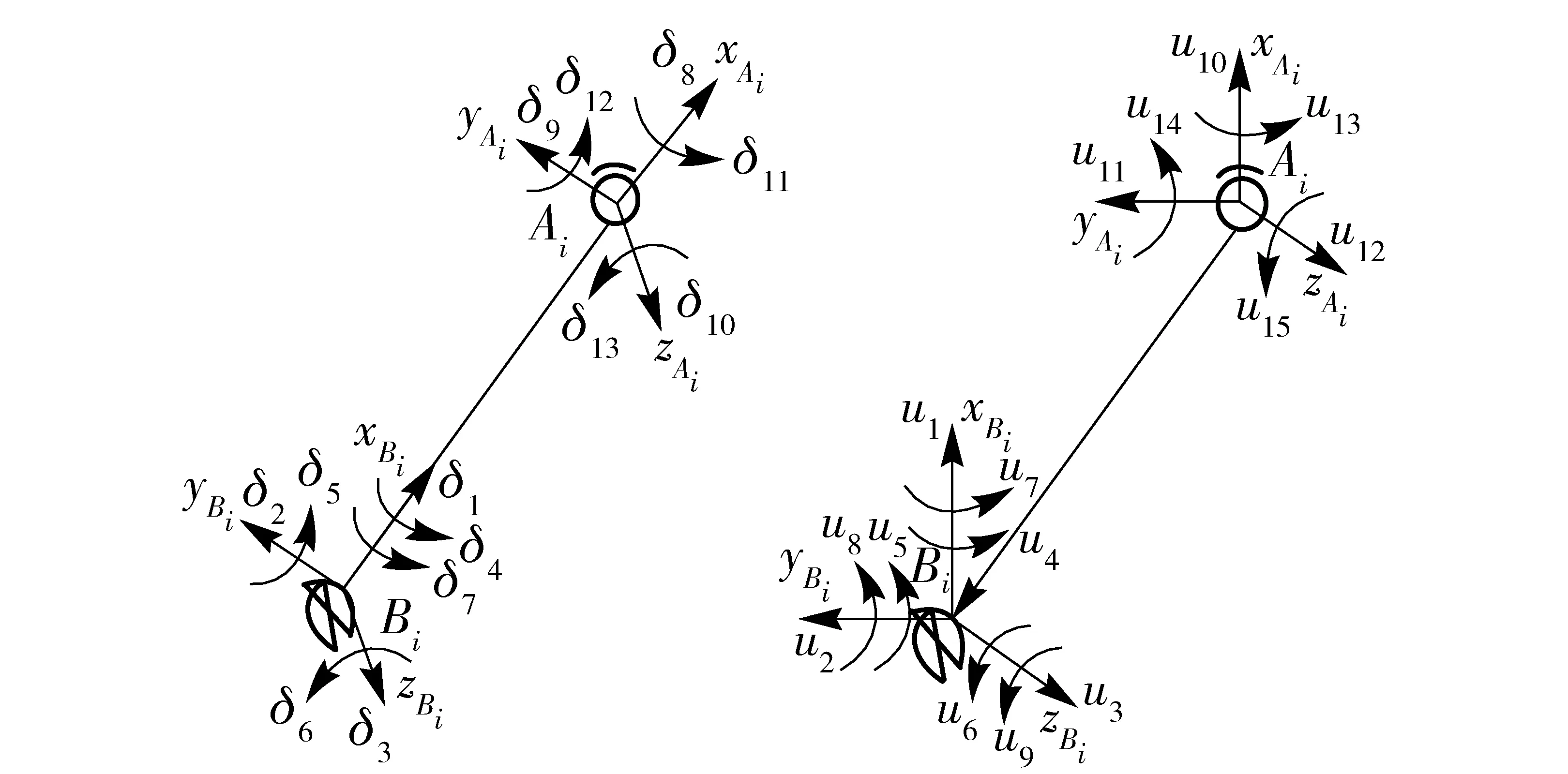
图3 支链AiBi的空间有限元模型Fig.3 Space finite element model of link AiBi

将上述广义坐标转换到系统坐标系中得到：ui=[u1…u15000]T，如图3(b)所示。由各支链变形引起的动平台PA1A2的角位移改变量可用广义坐标δP表示：

δP=[ΔαΔβΔγ]T,

(2)

式中：Δα、Δβ、Δγ分别为由弹性变形引起动平台3个方向上的微小角位移。

忽略单元截面的转动动能，则支链单元的动能包括平动动能和转动动能：

(3)

式中：m(x)为支链单元单位长度的密度，m(x)=ρA，A为梁单元的横截面积；L、ρ分别为单元的长度和密度；Wax(x,t)、Way(x,t)、Waz(x,t)分别为单元3个轴向的绝对弹性位移；Ip为单元对xB3轴的极惯性矩；δr为相对广义坐标向量；Me为单元质量矩阵，

(4)

N4为插值向量。

忽略单元的剪切变形能，则支链单元的势能为

(5)

式中：E、G分别为单元的压缩弹性模量、剪切弹性模量；Iy、Iz分别为单元横截面对两惯性轴的惯性矩；

(6)

(7)

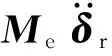
2.2 HUS柔性并联平台的空间约束关系

支链动力学方程(7)式是在单元坐标系中求得的，为了得到柔性并联平台系统的空间弹性动力学模型，需要完成3个步骤：1)将支链动力学由单元坐标系转换到系统坐标系中；2)获得支链单元和动平台的运动学以及动力学约束关系；3)计算系统坐标系下动平台的运动学方程。

连体坐标系B1x″B1y″B1z″B1与转换坐标系B1x′B1y′B1z′B1可以通过两个欧拉角β0、γ0变换，从B1x′B1y′B1z′B1坐标系到B1xB1yB1zB1坐标系可由T(45)完成转换，则从连体坐标系B1x″B1y″B1z″B1到B1xB1yB1zB1坐标系的转换矩阵可以表示为

TB=T(45)T(β0，γ0)，

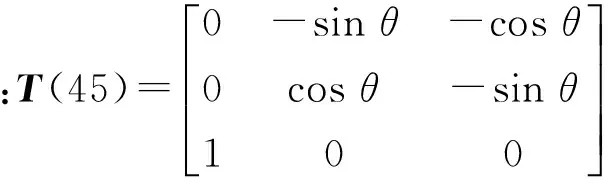
δi=TBui.

(8)

将(8)式代入弹性连杆模型(7)式可得

(9)

化简后得

(10)

连杆AiBi的局部坐标到系统坐标的转换关系分别可用(10)式进行表示。

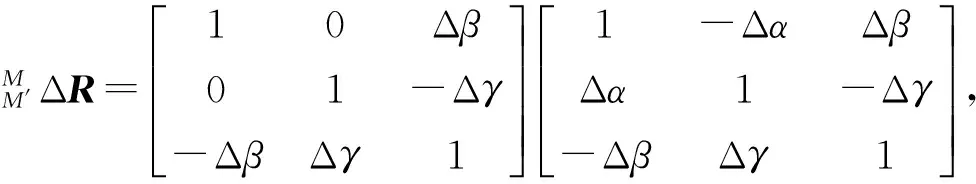
点A1和A′1在系统坐标系下的坐标分别为(xA1yA1zA1)T和(xA′1yA′1zA′1)T，则有

(11)

式中：A1M表示点A1在原位形坐标系下的坐标值，与变形后位形下的坐标值相等。

由弹性变形引起点A1的位移差为

(12)

式中：I为单位矩阵。

将位移差模型化简得

(13)

(13)式即为点A1的弹性位移与动平台的弹性角位移之间的约束关系。

动平台在外力和支链作用下做二自由度定点转动，则在单元坐标系中由牛顿- 欧拉方程得

(14)

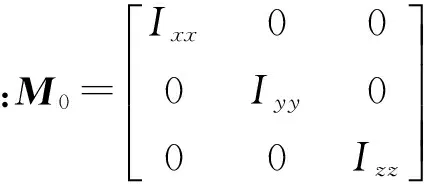
将(14)式方程转换到欧拉坐标系中，由欧拉坐标到单元坐标的转换公式为

(15)

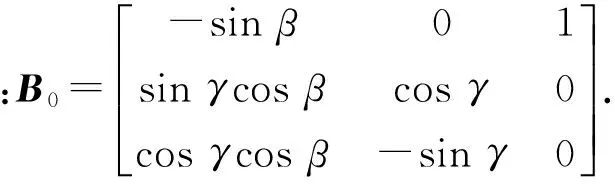
将(15)式代入(14)式中，可以得到动平台用欧拉角表示的动力学方程：

(16)

2.3 HUS柔性并联平台的空间动力学模型

系统广义坐标U*=[ui1…ui15ΔβΔγ]T，弹性杆广义坐标U*=[ui1…ui15]T，则由(13)式可得

Ui=RU*，

(17)

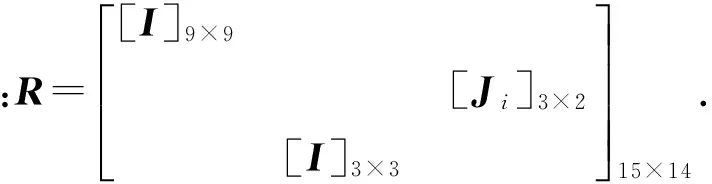
将(17)式代入(10)式可得

化简为

(18)

式中：Mi=RT(MeT)15×15R；Ki=RTKeTR.

(19)

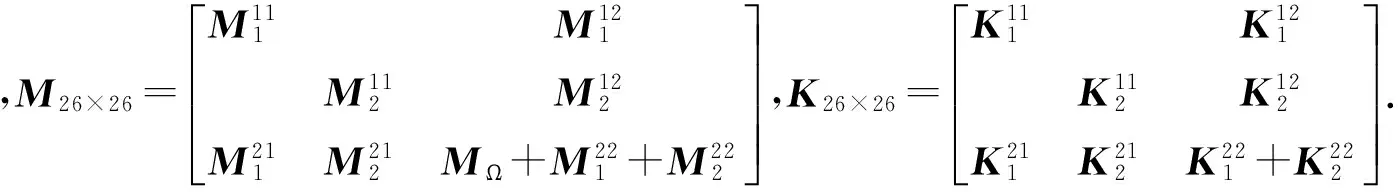
3 柔性动力学方程的数值求解与实验验证

系统的弹性动力学方程是一个强耦合、变系数的微分方程组，本文选择Newmark法进行有限元动力学求解。HUS柔性并联平台的OA1、OA2、OC1、OC2均为180 mm，连杆A1B1、A2B2长400 mm，OC2与y轴之间夹角为45°.

设定系统参数：材料为钢，密度ρ=7 800 kg/m3，抗压弹性模量E=210 GPa，剪切弹性模型G=80 GPa，弹性杆截面积A=0.001 6 m2，动平台的质量M0=40 kg，Δt= 0.1 ms，各构件的转动惯量如表1所示，表中Jx、Jy、Jz分别为构件对x、y、z轴的转动惯量。

假设动平台单轴转动，运动规律为

(20) 表1 构件转动惯量Tab.1 Moment of inertia of each part

动平台的弹性运动位移如图4所示，弹性角位移如图5所示，连杆的最大动应力如图6所示。

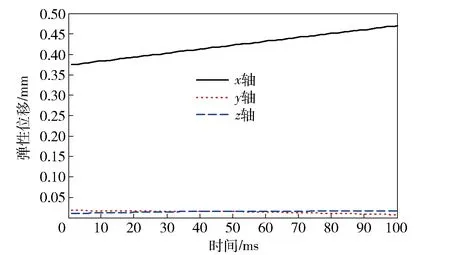
图4 动平台的弹性位移Fig.4 Elastic displacement error of moving platform

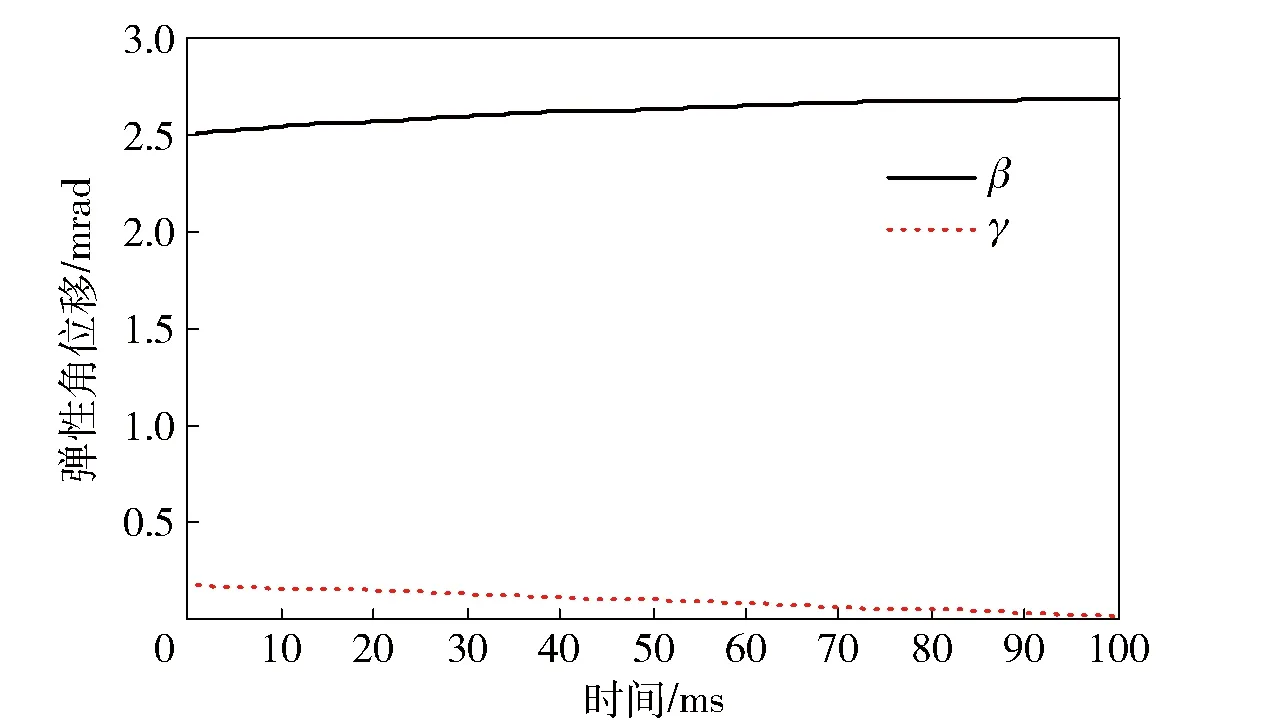
图5 动平台的弹性角位移Fig.5 Elastic angular displacement of moving platform

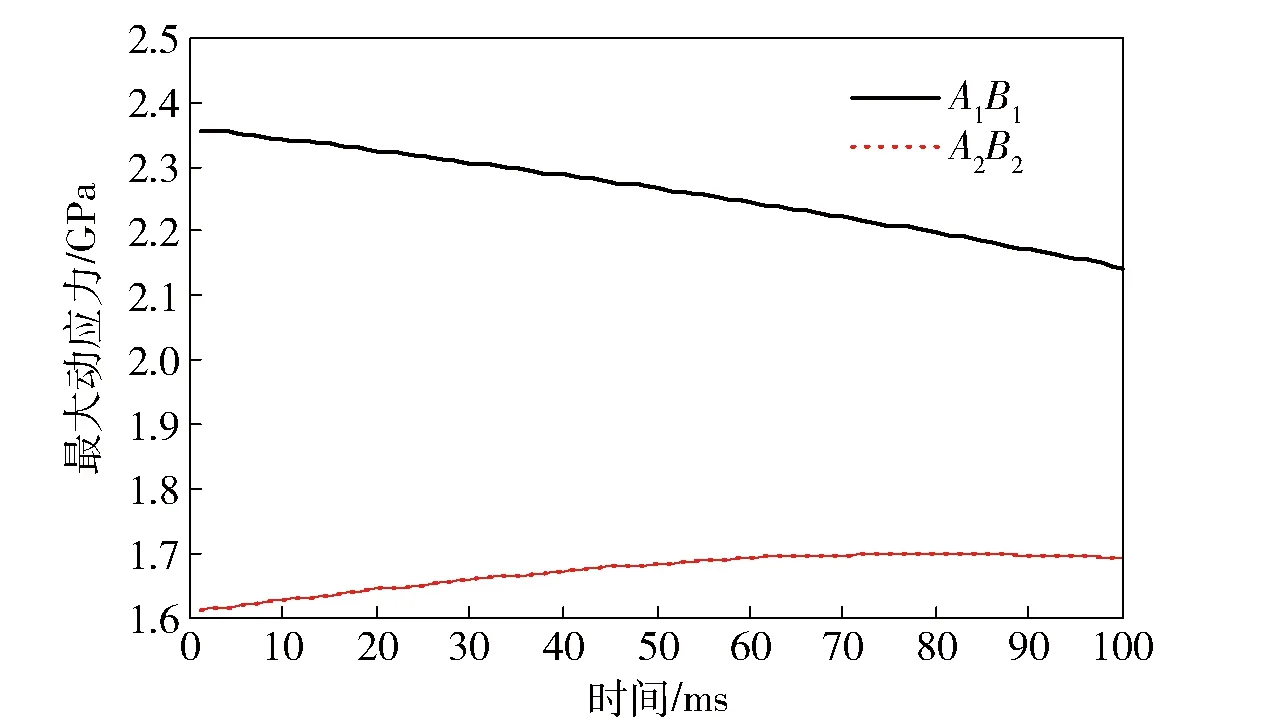
图6 连杆最大动应力曲线图Fig.6 Maximum dynamic stress curve of link

在系统运动过程中点A1在刚性位移的基础上产生弹性位移，图4描述了动平台与支链的连接点A1在x、y、z3个方向上的最大弹性位移的变化过程，给出了每个时刻弹性震荡的幅值。可见，3个方向弹性位移相差较大，其中x轴明显大于y轴和z轴，这是因为连杆Bi端的连接形式为虎克铰，在y、z方向受到虎克铰的约束作用，因此x方向的弹性位移与y轴和z轴明显不同。从图4中可以看出，x、y、z3个方向上的最大弹性位移分别为0.47 mm、0.018 mm、0.017 mm，显然在平台运动过程中弹性位移也在不断变化。

图5为动平台两个广义欧拉角的弹性角位移变化情况，由图中可以看出β变化比γ剧烈，这是因为β角在运动过程中耦合了γ角的变化，因此无论在变化频率还是在变化幅值上都会相对剧烈，其中β的最大值为2.7×10-3rad，γ的最大值为0.17×10-3rad. 图6为并联平台支撑连杆的最大应力变化情况，最大应力发生在连杆的B端，A1B1的最大应力均值大于A2B2，连杆L2变化范围较连杆A1B1大，在系统运动过程中，弹性杆的最大应力分别是2.35 GPa、1.7 GPa.

图7所示为实验室样机测试实验，通过伺服电机驱动加载，电机转速由20 r/min变化到140 r/min，记录动平台的姿态变化，数据采集通过两个航姿测量系统完成，基座上的航姿测量系统用来完成对动平台测量数据的修正。

图7 样机测试试验Fig.7 Experiment of prototype

图8所示为由测量数据得到的3个方向的弹性位移，从图中可看出x轴的弹性位移明显高于y轴、z轴，与仿真分析一致，验证了数值建模的有效性。电机转速在140 r/min时，弹性位移在幅值和频率上均表现明显，电机转速从120 r/min减小时，弹性位移收敛速度变慢，弹性位移趋于稳定，变化不明显。

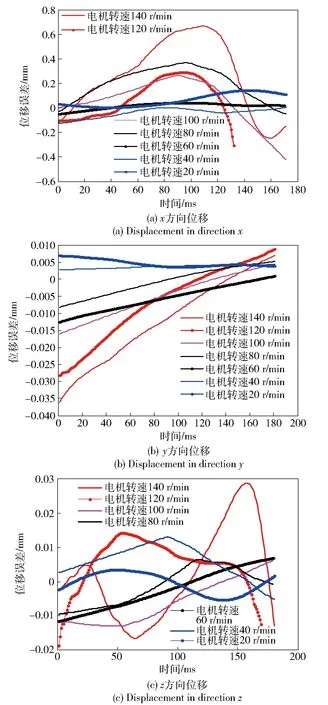
图8 样机弹性位移Fig.8 Elastic displacement of prototype

海上HUS柔性并联平台承担海面探测、预警等任务，具有一定的防御和攻击能力，其平台上装有负载设备，由于弹性连杆引起的平台微小角位移差影响了负载设备的定位和瞄准精度。弹性角位移引起的负载瞄准位置偏差为

x=T(β、γ)Lm-Lm，

(21)

式中：Lm为负载设备的工作距离。

Lm一般在6 km左右，转换矩阵T是由β、γ形成的弹性角位移矩阵，则由(21)式可知，弹性角位移引起的最大位置偏差1.35 m，同时应该注意的是，该误差仅仅考虑了弹性形变，而没有考虑系统结构的制造误差等。因此系统在进一步的结构优化设计中应着重加强支链连杆的刚性，同时在系统的控制结构中考虑柔性模型引起的弹性变形误差，提高控制精度。

4 结论

本文基于等截面梁单元模型，利用Lagrange方程建立了空间连杆的弹性动力学模型。

1)分析了空间两自由度连杆的弹性广义坐标变化情况，由两自由度的欧拉变换推导并联机构弹性连杆的空间位置变换方程，结合运动学和动力学约束条件，推导了海上HUS柔性并联平台的空间弹性动力学方程，

2)仿真分析结果表明：x轴弹性位移大于y轴和z轴；弹性角位移β在运动过程中耦合了γ角的变化，β变化比γ更加剧烈；弹性杆的最大应力分别是2.35 GPa、1.7 GPa，最大应力发生在连杆的B端。

3)实验测量结果与仿真分析一致，验证了数值建模的有效性；电机转速在140 r/min时，弹性位移在幅值和频率上变现明显，从120 r/min减小时，弹性位移变化较小，趋于稳定。

4)分析了平台负载在弹性角位移作用下形成的瞄准位置偏差，负载设备工作距离6 km时，最大位置偏差1.35 m，对进一步研究海上HUS柔性并联平台的动态特性、优化设计和系统控制具有一定的参考意义。

References)

[1] 王振宇, 张彪, 刘国华. 浮式海洋结构的应用与背景[J]．中国海洋平台, 2009, 24(1): 10-14. WANG Zhen-yu, ZHANG Biao, LIU Guo-hua. Application and foreground of the floating structures[J]. China Offshore Platform, 2009, 24(1): 10-14. (in Chinese)

[2] 卢其进, 杨和振. 海洋风电支撑结构的随机性动力优化设计[J]．振动与冲击, 2013, 32(17): 46-51. LU Qi-jin, YANG He-zhen. Probabilistic dynamic optimization design for support structure of offshore wind turbines[J]. Journal of Vibration and Shock, 2013, 32(17): 46-51. (in Chinese)

[3] 胡自伟, 陈晖, 刘江平. 踏浪精灵—水面无人舰艇[J]. 现代军事, 2004, 32(17): 46-51. HU Zi-wei, CHEN Hui, LIU Jiang-ping. Sea elf—surface unmanned ships[J]. Modern Military, 2004, 32(17):46-51. (in Chinese)

[4] 刘晓, 赵铁石, 边辉, 等. 大型舰载稳定平台机构及优化设计[J]. 机器人, 2013, 35(3): 339-345. LIU Xiao, ZHAO Tie-shi, BIAN Hui, et al. Optimization design of a large-scale mechanism for ship-based stabilizing platform[J]. Robot, 2013, 35(3):339-345. (in Chinese)

[5] 金振逸, 马少杰. 基于线性波浪理论的海上浮动平台受力及运动分析[J]. 四川兵工学报, 2011, 32(8): 135-137. JIN Zhen-yi, MA Shao-jie. Analysis of force and motion of maritime floating platform based on linear wave theory[J]. Journal of Sichuan Ordnance, 2011, 32(8): 135-137.(in Chinese)

[6] 赵亮. 一种2UPS-UPR并联机床的设计理论及关键技术研究[D]. 沈阳:东北大学, 2010. ZHAO Liang. Study on design theory and key technology of 2UPS-UPR parallel machine tool[D]. Shenyang:Northeastern University, 2010. (in Chinese)

[7] 胡胜海, 郭春阳, 余伟, 等. 基于变胞原理的舰炮装填机构刚- 柔耦合动力学建模及误差分析[J]. 兵工学报, 2015, 36(8): 1398-1404. HU Hai-sheng, GUO Chun-yang, YU Wei, et al. Rigid-flexible coupling dynamic modeling and error analysis of loading mechanism of naval gun based on metamorphic principle[J]. Acta Armamentarii, 2015, 36(8): 1398-1404. (in Chinese)

[8] 张绪平, 余跃庆. 综合考虑关节及杆柔性的空间机器人动力学分析[J]. 机械科学与技术, 1998, 17(5): 775-778. ZHANG Xu-ping, YU Yue-qing. Dynamic analysis of spatial manipulators considering joint and link flexibility[J]. Mechanical Science and Technology, 1998, 17(5):775-778. (in Chinese)

[9] 陈江义, 郝雪清, 范利格, 等. 计入构件柔性和铰链间隙的并联机构动力学分析[J]. 机床与液压, 2013, 41(23): 28-31. CHEN Jiang-yi, HAO Xue-qing, FAN Li-ge, et al. Dynamic analysis of parallel mechanism with clearance revolute joint and flexible component[J]. Machine Tool and Hydraulics, 2013, 41(23): 28-31. (in Chinese)

[10] 吕帮俊, 彭利坤, 熊先锋. 考虑构件弹性的电动Stewart并联机构刚度建模与仿真[J]. 振动与冲击, 2013, 32(12): 135-149. LYU Bang-jun, PENG Li-kun, XIONG Xian-feng. Stiffness modeling and simulation for an electric Stewart parallel mechanism considering elasticity of components[J]. Journal of Vibration and Shock, 2013, 32(12): 135-149. (in Chinese)

[11] 谢克峰, 张合, 李豪杰, 等. 海上漂浮2-HUS/U并联平台动力学分析[J]. 农业机械学报, 2016, 47(1): 362-368. XIE Ke-feng, ZHANG He, LI Hao-jie, et al. Dynamic analysis of offshore floating 2-HUS/U parallel platform[J]. Transactions of the Chinese Society for Agricultural Machinery, 2014, 45(3): 293-298. (in Chinese)

[12] 李珂翔, 张合. 并联光电跟踪平台建模与工作空间闭环控制[J]. 农业机械学报, 2014, 45(3): 293-298. LI Ke-xiang, ZHANG He. Modelling and closed-loop control in workspace of parallel optoelectronic tracking platform[J]. Transactions of the Chinese Society for Agricultural Machinery, 2014, 45(3): 293-298. (in Chinese)

[13] 落海伟, 张俊, 王辉, 等. 3-RPS并联机构弹性动力学建模方法[J]. 机器人, 2014, 36(6): 737-743, 750. LUO Hai-wei, ZHANG Jun, WANG Hui, et al. An elastodynamic modelling for a 3-RPS parallel kinametic machine[J]. Robot, 2014, 36(6): 737-743, 750. (in Chinese)

[14] Wang X Y, Mills J K. Dynamic modelling of a flexible-link planar parallel platform using a substructuring approach[J]. Mechanism and Machine Theory, 2006, 41(6): 671-687.

[15] 张清华, 张宪民. 平面3-RRR柔性并联机器人动力学建模与分析[J]. 振动工程学报, 2013, 26(2): 239-245. ZHANG Qing-hua, ZHANG Xian-min. Dynamic modeling and analysis of planar 3-RRR flexible parallel robots[J]. Journal of vibration Engineering, 2013, 26(2): 239-245. (in Chinese)

[16] Piras G, Cleghom W L. Dynamic finite-element analysis of a planner high-speed, high-precision parallel manipulator with flexible links[J]. Mechanism and Machine Theory, 2005, 40(7): 849-862.

[17] 刘善增, 余跃庆, 杨建新, 等. 3-RRC并联柔性机器人的动力学分析[J]. 振动与冲击, 2008, 27(2): 157-161, 184. LIU Shan-zeng, YU Yue-qing, YANG Jian-xin, et al. Dynamic analysis of a 3-RRC parallel flexible manipulator[J]. Journal of Vibration and Shock, 2008, 27(2): 157-161, 184. (in Chinese)

[18] Xue M D, Duan J, Xiang Z H. Thermally-induced bending- torsion coupling vibration of large scale space structures[J]. Computational Mechanics, 2007, 40(4):707-723.

Space Dynamic Modelling and Analysis of Offshore HUS Flexible Parallel Platform

XIE Ke-feng1, ZHANG He1, LIU Shan-zeng2, LI Hao-jie1

(1.Ministerial Key Laboratory of ZNDY, Nanjing University of Science and Technology, Nanjing 210094, Jiangsu, China;2.School of Mechanic Engineering, China University of Mining and Technology, Xuzhou 221116, Jiangsu, China)

The space elastic dynamic modelling of parallel platform is created for the elastic deformation and the load pointing displacement error of support link due to the rapid stabilization and large load of offshore HUS flexible parallel platform. Space elastic link is modelled by modal function and space equal section beam element model. The link based on hook joint and ball joint has two degrees of freedom space movement. The transformation matrix of two degrees of freedom between space element coordinate and system coordinate is derived. The kinematic and dynamic constraints of platform are used to establish the space elastic dynamic equations of HUS flexible parallel platform. The elastic dynamic equations are discretely solved by Newmark method. The elastic dynamic response of platform and the maximum dynamic stress of support link are analyzed. And the dynamic test experiment is conducted. The results show that the maximum displacement of support point by elastic deformation is 2.45 mm, and the error of axisxis significantly greater than those of axesyandz. Experimental results are consistent with the simulated results, thereby validating the effectiveness of the numerical model. The influence of elastic deformation on load pointing accuracy is analyzed, and the maximum position error due to elastic angular displacement is 1.35 m.

mechanics; flexible parallel platform; space dynamic modelling; elastic deformation; elastic link

2016-05-05

国家自然科学基金项目(51475243)；江苏省普通高校研究生科研创新计划项目(KYLX15-0340)

谢克峰(1988—), 男, 博士研究生。E-mail: xiekefeng.ok@163.com

张合(1957—)，男，教授，博士生导师。E-mail: hezhangz@njust.edu.cn

10.3969/j.issn.1000-1093.2017.03.013

TJ610.3+1; TP242.3

A

1000-1093(2017)03-0512-08