Artificial Noise Aided Polar Codes for Physical Layer Security

China National Digital Switching System Engineering and Technological R&D Center, Zhengzhou 450002, China

I. INTRODUCTION

Since 5G network is expected to be heterogeneous, the security paradigms protecting the confidentiality of wireless communications remain elusive [1]. Recently, physical layer security (PLS) has been studied as a promising technique that guarantees secure wireless communications by exploiting the characteristics of wireless channels [2][3].

There are two main categories of PLS techniques: 1) secret key generation from the wireless communication medium over public channels [4]; and 2) secure transmission strategies by exploiting the inherent randomness of communication channels without a secret key.As keyless security techniques, the second category has drawn great attention and a large amount of research has been done. Artificial noise and beamforming techniques are often used in point-to-point MIMO scenarios, and they have been proved to effectively improve the secrecy capacity and guarantee the confidential communication between legitimate users [5][6]. In relay-aided communication scenarios, cooperative forwarding and cooperative jamming are usually adopted to guarantee PLS [7]. And the problems of source-relay selection and forwarding power allocation are discussed in [8][9]. Secrecy coding based on the randomness of wireless channels is also an important PLS technique which guarantees communication security and reliability simultaneously [10]. Many secrecy codes, such as coset codes [11], nested codes [12] and lattice codes [13], have been proved to approach secrecy capacity in theory. However the design of practical secrecy coding scheme is still an open issue.

The paper proposes an artificial noise (AN)aided polar coding algorithm to improve the secrecy rate.

Polar codes have been studied for decades[14], and recently are adopted in the enhanced mobile broadband (EMBB) control channel for 5G communication systems. The property of channel polarization makes them suitable for PLS. The strong and weak theoretical secrecy limits of polar codes for PLS are studied in [15] and [16], respectively. Then, practical polar coding methods are proposed for finite coding length, such as the puncturing polar codes [17], the ARQ-based polar coding schemes [18][19] and the relay aided secrecy polar coding methods [20][21]. However, all these methods are under the assumption that the wiretap channel is degraded with respect to the legitimate channel. When the quality of the wiretap channel is close to (or even better than) that of the legitimate channel, secrecy rate is rather low, and even goes to zero.Therefore, polar coding combined with AN is studied to improve the secrecy rate. To manage interference in favor of the legitimate receiver, [22] and [23] design the AN in the null space of the legitimate channel, and improve the secrecy rate by debasing the SINR of the eavesdropper. However, these methods bring extra power expense, and are invalid when the spatial freedom does not exist.

In this paper, we present a novel AN-aided polar coding algorithm. Since the confidential bits in secrecy polar coding is only known to the legitimate receiver, we adopt the confidential bits as AN to deteriorate the receiving reliability of eavesdropper, thus improving the secrecy rate. The main contributions of this paper are as follows.

● An AN aided polar coding model is proposed, where the confidential bits of last transmission code block are adopted as AN to inject into the current codeword. In this way, the legitimate users can eliminate AN from the jammed codeword, while eavesdropper cannot. The proposed algorithm can work without spatial freedom, which is quite different form the typical null space AN design in [22][23]. Moreover, since AN is directly added on the codeword before modulation, additional power is not needed,which is also different from [22] [23].

● Since AN is shorter than the codeword, a low complexity suboptimal jamming positions selection algorithm is proposed based on the structure of polar codes, where the decoding performance of eavesdropper can be deteriorated to the worst, thus further improving the secrecy rate.

● The secrecy rate of the proposed AN-aided polar coding algorithm is derived. Theoretical and simulation results demonstrate that the proposed algorithm outperforms the random selection method and the method without AN.

The remainder of this paper is structured as follows: Section II outlines problem formulation. Section III gives the detailed AN aided polar coding algorithm. Section IV conducts a theoretical analysis to show the security of our proposed algorithm. Section V provides the analyses of simulation results. Section VI summarizes the paper.

II. PROBLEM FORMULATION

i=1,2,…,N. As N→∞, the polarized bit channelis either noiseless or pure-noisy

The construction of polar codes is based on a phenomenon referred to as channel polarization [14]. With channel polarization effect, the polar decoding performance of a certain input position is tightly bounded with the channel characteristic. Hence polar codes have been employed as secrecy codes at physical layer[15-21].

In the secrecy polar coding scheme, the N recursive uses of transmission channel W can be polarized into bit channels WN(i)after channel polarization, where N=2n, n≥0, and([14] Eq. (5)). Assume the legitimate channel is W and the degraded wiretap channel is W*.By exploiting the above polarization properties, the polarized channels can be divided into three subsets: the first one with indices i∈S used to transmit the confidential bits, the second one with indices i∈R used to transmit the random bits and the third one with indices i∈F flooded with frozen bits [15]. In order to meet the reliability and security restrictions of polar codes for PLS, S, R and F are given by

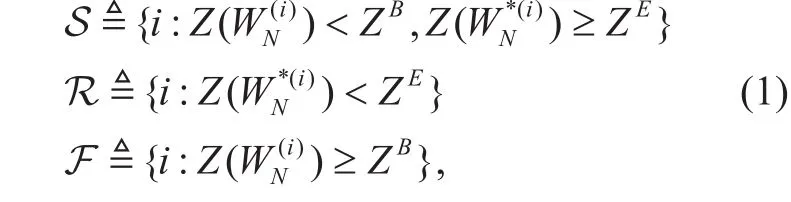
Mahdavifar has proved that secrecy polar coding with infinite code length can approach the secrecy capacity in [15]. However, in practical finite code length scenarios, there are many polarized channels between the states of noiseless and pure-noisy because of the incomplete channel polarization process. So the reliable polarized legitimate channels used to transmit the confidential bits are quite small,i.e.is smaller than expected. As a result,the secrecy rate of finite code length polar coding is far from the secrecy capacity [17],which is difficult to fulfil the security requirements of high-speed communications, such as 5G communications. Therefore the design of high-rate secrecy polar codes with finite code length is an urgent issue.

III. AN-AIDED POLAR CODING

AN is one of the most classical methods to improve the security performance by confusing the eavesdropper. In this section, we propose an AN aided polar coding algorithm to deteriorate the wiretap channel and improve the secrecy rate.

3.1 Secrecy coding model

Based on the channel polarization effect, the confidential bits (with indices i∈S) can only be reliably decoded by the legitimate receiver.Therefore, we adopt the confidential bits transmitted over last code block as AN in current block. So the legitimate user can eliminate AN from the jammed codeword, but the eavesdropper cannot. The system model is shown in figure 1.

A block fading model is considered for the wiretap channel, i.e. the channel coefficient is assumed to be constant within each coherence time interval. For each code block, transmitter (Alice) encodes the information u into the codeword x. After that, AN is injected into x and we obtain the transmitted vector s=x⊕v, where⊕denotes the module-2 sum, v is the extended vector generated by the AN vector uˆSof the last code block, virepresents the ith column of v. The block indices are omitted here. For simplicity, we denote the length of uˆSis k. It is obvious that k is shorter than code length N. We extend uˆSto length N by zero-padding. When the i th transmitted symbol is not injected with uˆS,we have vi=0. Then the received symbols of the legitimate user (Bob) and the eavesdropper(Eve) are obtained as follows:

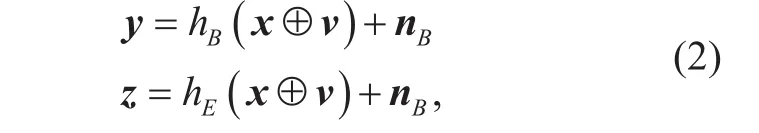
where hBand hEare the channel coefficients of Bob and Eve, respectively. nBand nEare i.i.d. Gaussian white noises with variances σB2and σE2, respectively. Since Bob has the knowledge of v, he can eliminate v in (2),and get

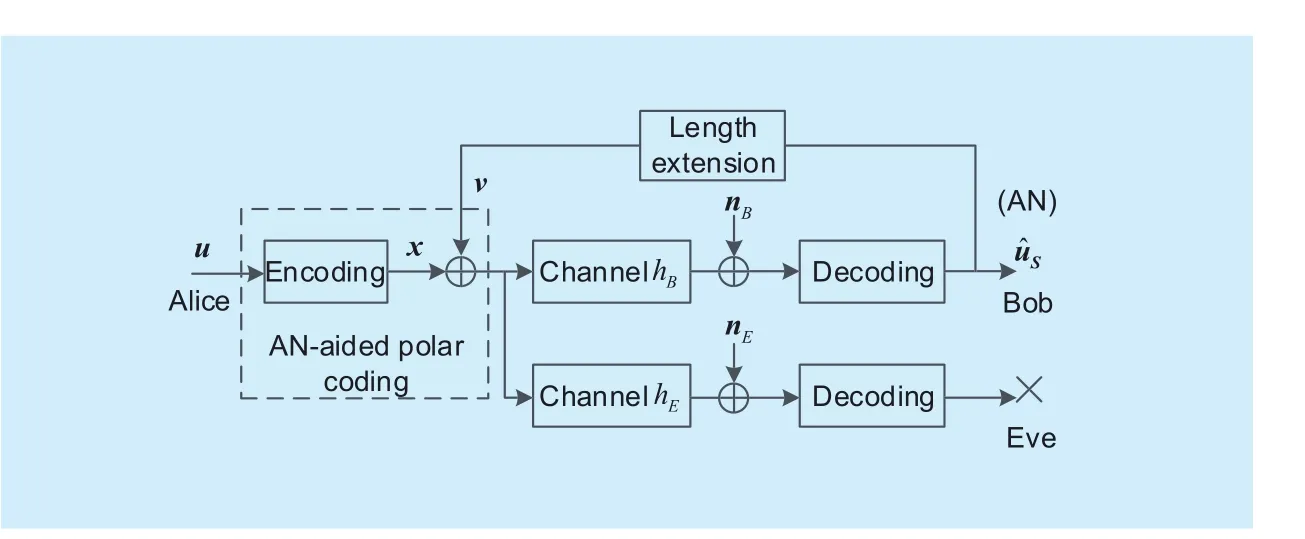
Fig. 1 AN aided secrecy coding model over wiretap channels

3.2 Jamming positions selection

From [14], the channel transition probability of polarized channel WN(i)relies on all the polarized channels WN(j)with j＜i. That means the decision of information bit uibased on the hypothesis thathas been decoded correctly. This property leads to an error propagation phenomenon. So the eavesdropper will be confused even a small fraction of the codeword is jammed.

Assume J is the index set of the channels injected with AN. From figure 1, since Eve can only receive x⊕v, without the knowledge of AN vector, he gets nothing about the symbol xi, i∈J. Therefore the Bhattacharyya parameters of the jammed bit channels of Eve can be expressed as

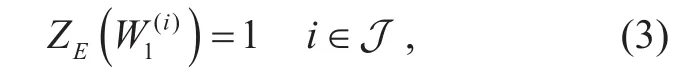
According to [24], the Bhattacharyya parameters of fading channel can be expressed as an exponential function of the SNR. The signal transmitting power is denoted as Pt.Then SNR of each bit channels of Bob is given by, and the SNR of Eve’s bit channel that padded by zero is given by. Finally we have

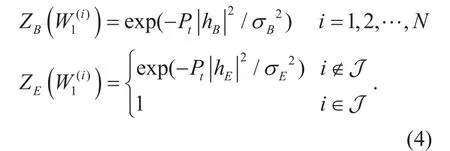
Lemma 1[24]: For a polarized bit channel, i=1,2,…,N, we have: 1)The lower and upper bound ofis continuous monotonically increasing with respect to each,i=1,2,…,N.

The monotonicity of the lower and upper bound of Z(WN(i)) is shown in Lemma 1.Based on it, the monotonicity ofcan also be proved. Finally we have Corollary 1.

Corollary 1: For a polarized bit channel, i=1,2,…,N, if any of the transmission channel W1jis deteriorated, j=1,2,…,N,thenis increased.

From Corollary 1, as long as parts of the transmission channels are jammed by AN,all the polarized bit channels will be deteriorated. So, despite that the length of AN vector is shorter than code length N, it is feasible to utilize AN to worsen the quality of wiretap channel and improve the security performance. However, different AN jamming positions have different effect on the decoding accuracy. Although random selection of AN jamming positions is a simple way, its security performance is not optimal. Therefore, Bhattacharyya parameter is adopted to measure the influence of AN on the information bits, and a novel jamming positions selection algorithm is introduced next.

Recall the definition of Bhattacharyya parameters in [14],can be written as a function depending onHowever, since the output alphabet increased exponentially, it is difficult to obtain the exactHere we use, the upper bound ofmentioned in [24], replace the parameters, i.e.

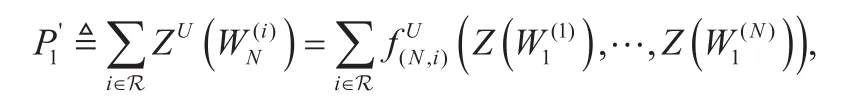
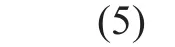
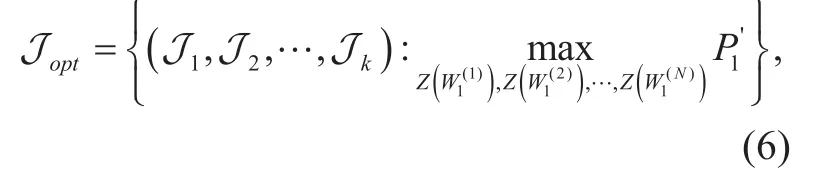
where Joptis the optimal jamming position index set, Jmis the mth element of Jopt,1≤m≤k. Unfortunately, the number of all the possible selection patterns of J isThis number will grow extremely large under practical configuration of N and k, so it is difficult to obtain Jopt.

Therefore we propose a low complexity suboptimal jamming positions selection algorithm based on the greedy algorithm. Only one jamming position is selected in our selection algorithm during each iteration. Thus k iterations are needed in our algorithm. For the first iteration, all the N transmission channels are available to be jammed. We calculate eachwith every transmission channel jammed in turn. After N calculations, the best jamming position iˆ that maximizeis found out, and put iˆ into set J. Then, for the mth iteration,the previous (m−1) jamming positions have been determined. And there are (N-m+1)transmission channels available to be jammed.Similarly, we calculate eachwith every remaining transmission channel jammed in turn and find out the mth jamming position. In this way, all the k jamming positions are selected after k iterations. The detailed algorithm is shown in algorithm 1.

The complexity of this algorithm chiefly comes from the calculation of(step 7). Since each iteration determines one jamming position, only k(2N−k+1)/2 calculations are required. This complexity is much lower than the exhaustive searching oftimes.

3.3 Procedure of AN-aided polar coding

Suppose Eve is also an authorized user in our transmission model, but he is not the desired receiver of the confidential message. Therefore the channel coefficient of wiretap channel is available for Alice. This assumption is widely used in the past researches on secrecy polar coding [15-18][22]. Based on the discussion of subsection 3.2, our AN-aided polar coding algorithm mainly consists of three steps: channel estimation, jamming positions selection,and noisy signal transmission.

Step 1: In the channel estimation step, the transmitter and the receiver send the same known pilot sequence in turn. Therefore, Alice obtains the estimates hBand hE. Bob and Eve only have their own channel coefficient.

Step 2: In the jamming positions selection step, Alice initializes the corresponding parameters according to the channel coefficient hBand hE, and then determines the jammingposition indices J by the algorithm proposed in 3.2.

Algorithm 1 Jamming positions selection algorithm

Step 3: In the noisy signal transmission step, we inject AN into the transmission bit channels with indices J. However, since AN is injected, the initial Bhattacharyya parameters are renewed by Eq. (4), and then the polarized channel indices sets are updated to S',R', F'(Eq. (1)). Finally, the confidential bits are transmitted over S', and become the AN sequence of the next block (see figure ).

The jamming positions in step 2 can be directly transmitted to Bob over broadcast channel. Therefore, Bob is able to eliminate AN by utilizing the jamming positions and the known confidential bits of the last code block, and then decode the current codeword with no error. However, since Eve knows nothing about the confidential bits of the last code block,even if he knows the jamming positions, he cannot eliminate AN and decode the current codeword.

IV. SECURITY ANALYSIS

In this section, we discuss the secrecy rate that the proposed AN-aided polar coding algorithm can achieve.

Lemma 2[25]: For any fixed δ∈(0,1),as N goes infinity, the fraction of indices i∈{1,2,…,N } for whichgoes to

Fig. 2 Block diagram for AN-aided polar coding algorithm

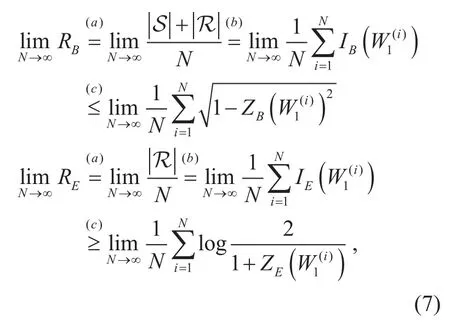
It is noticed from polar coding that the code rate of Bob and Eve can be expressed as respectively. Note that, step (a) follows from the degraded wiretap channel assumption and restrictions shown in Eq. (1), step (b) from the conclusion of Lemma 2, and step (c) from the conclusion of Proposition 1 in [14]. Hence, the secrecy rate, denoted as RS, can be expressed as

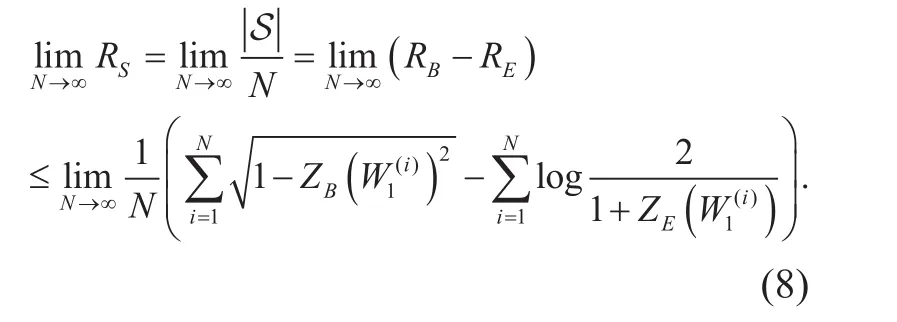
Corollary 2: As code length N and block number T go to infinity, the secrecy rate of our proposed AN-aided polar coding algorithm is

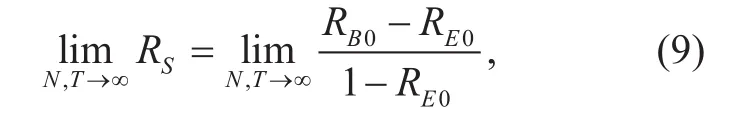
where RB0and RE0are the code rates of Bob and Eve without AN.

Proof.The proof is derived in Appendix A.

The secrecy rate without AN is defined as RS0.Therefore, we have

According to Eq. (9), it is obviously thatTherefore, it is proved that the proposed algorithm has a higher secrecy rate than transmission without AN. In addition, it is easily to drive thatfrom (9). Thus,the secrecy rate of our proposed algorithm satisfies

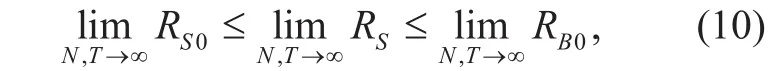
where the equality holds when RE0= 0.

V. SIMULATION RESULTS

In this section, we validate the performance of the proposed AN-aided polar coding algorithm by comparing the secrecy rate and Eve’s bit error rate (BER) with other algorithms.

The simulation results shown in this section are averaged over 106Monte Carlo simulations. For simplicity, we consider the noise variances of Bob and Eve are both 1, i.e.. The signal transmitting powerare assumed to be 0.5 and 0.1, respectively. There are T=10 blocks within each coherence time interval. Suppose the polar codes with length N=128, the reliability and security thresholds are ZB=10−5and ZE=0.9, respectively. Another two methods are adopted here for comparison, i.e.the random AN positions selection method and the transmission method without AN. The random selection method has the same secrecy coding model as our method, however AN positions are selected randomly among the N positions.

The secrecy rate curves are depicted in figure 3. The abscissa shows the block number,and secrecy rate is the ratio of confidential bits number and N. When block number is 1,AN has not injected into the codeword, so the secrecy rates of the three methods are equal.From the second block, the secrecy rates of the two methods with AN increase rapidly. This is consistent with the conclusion of section IV.However, for the transmission method without AN, it stays constant. Figure 3 also shows that our proposed algorithm has a better performance than the random selection method. It is because our algorithm chooses the best positions that further deteriorating the decoding performance of Eve.

Fig. 3 Secrecy rate for different algorithms of polar coding

Fig. 4 Indices of AN jamming positions

Figure 4 shows the indices of AN jamming positions by our selection algorithm. The abscissa is the position indices from 1 to N. For simplicity, we only plot the even blocks. We can see from figure 4, AN are concentrated in the positions with large indices. This is because the reliable polarized channels of Eve are concentrated in these positions. Therefore,jamming in these positions will further deteriorate Eve’s receiving reliability. In addition,for any 1≤t1＜t2≤T , the selected AN indices set of block t1(J(t1)) is a subset of J(t2).This is because the initial channel parameters of each block are the same (within the coherence time interval), and our jamming positions selection algorithm finds the best AN positions one by one. According to the discussion in section IV, the AN bits number of block t1is less than or equal to that of block t2. Therefore we have J(t1)⊂J(t2).

In secrecy polar coding, the transmission positions of the confidential bits vary according to Eq. (1). Therefore, the reliability of Bob always meets the Bhattacharyya threshold ZB. However, the reliability of Eve can be decreased by the AN. The BER curves of Eve are depicted in figure 5. Here, we consider the average BER of all the non-frozen bits of Eve.Figure 5 illustrates our algorithm can effectively increase Eve’s BER. When block number is 9, Eve’s BER is 0.475, which is much higher than the random selection method and the transmission method without AN. The reliability reduction of Eve shows the security improvement from another aspect.

Fig. 5 BER of Eve for different algorithms of polar coding

VI. CONCLUSIONS

An AN-aided polar coding algorithm is proposed to improve the secrecy rate of polar codes for PLS. In this algorithm, the confidential bits of the last transmission code block are adopted as AN and injected into the current codeword to confuse the eavesdropper. Since the length of AN is shorter than the code length, the optimization problem of jamming position selection is investigated to further deteriorate Eve’s receiving reliability. And we present a suboptimal solution based on the greedy algorithm, which has a much lower complexity than exhaustive searching. The performance of the presented algorithm is verified by the theoretical and simulation results.

Appendix

A. Proof of Corollary 2

Assume t1,t2→∞ and t2=t1+1. As N→∞, we have

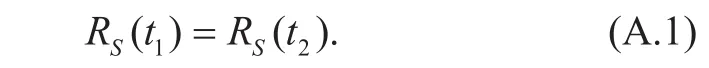
According to (7) and (8), we have

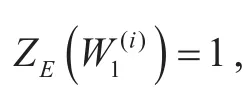
The number of AN bits in block t2is N⋅RS(t1). We can get the simplification of(A.2)

By substituting (A.1) into (A.3), the conclusion of Corollary 2 is proofed.

ACKNOWLEDGEMENTS

This work was supported in part by China’s High-Tech Research and Development Program (863 Program) under Grant No.2015AA01A708, and National Science Foundation for Young Scientists of China under Grant No. 61501516.

[1] P. Z Fan, J. Zhao, and L. I Chih, “5G High Mobility Wireless Communications: Challenges and Solutions,” China Communications, vol. 13, no.S2, 2017, pp. 1-13.

[2] Y. L Zou, J. Zhu, X. B Wang, et al, “A Survey on Wireless Security: Technical Challenges, Recent Advances, and Future Trends,” Proceedings of the IEEE, vol. 104, no. 9, 2016, pp. 1727-1765.

[3] X. M Chen, W. K Ng, W. Gerstacker, et al, “A Survey on Multiple-antenna Techniques for Physical Layer Security,” IEEE Communications Surveys & Tutorials, vol. 19, no. 2, 2017, pp.1027-1053.

[4] J. Q Zhang, T. Q Tuong, A. Marshall, et al, “Key Generation from Wireless Channels: A Review,”IEEE Access, vol. 4, 2016, pp. 614-626.

[5] X. S Ji, X. L Kang, K. Z Huang, et al, “The Full-duplex Artificial Noise Scheme for Security of a Cellular System,” China Communications, vol.12, no. S1, 2015, pp. 150-156.

[6] S. H Lai, P. H Lin, S. C Lin, et al, “On Optimal Artificial-noise Assisted Secure Beamforming for the Multiple-input multiple-output fading eavesdropper channel,” Proc. 2012 IEEE Wireless Communications and Networking Conference(WCNC), 2012, pp. 513-517.

[7] Y. L Zou, J. Zhu, X. B Wang, et al, “Improving Physical-layer Security in Wireless Communications Using Diversity Techniques,” IEEE Network,vol. 29, no. 1, 2015, pp. 42-48.

[8] Y. L Zou, B. Champagne, W. P Zhu, et al, “Relay-selection Improves the Security-reliability Trade-off in Cognitive Radio Systems,” IEEE Transactions on Communications, vol. 63, no. 1,2015, pp. 215-228.

[9] X. M Li, T. Jiang, S. G Cui, et al, “Cooperative Communications Based on Rateless Network Coding in Distributed MIMO Systems,” IEEE Wireless Communications, vol. 17, no. 3, 2010,pp. 60-67.

[10] A. D Wyner, “The Wiretap Channel,” AT&T Bell Laboratories Technical Journal, vol. 54, no. 8,1975, pp. 1135-1387.

[11] L. H Ozarow and A. D Wyner, “Wiretap Channel II,” Bell System Technical Journal, vol. 63, no. 10,1984, pp. 2135-2137.

[12] Y. Cassito and Z. Bandic, “Low Complexity Wiretap Codes with Security and Error-correction Guarantees,” Proc. IEEE Information Theory Workshop, 2010, pp. 1-5.

[13] J. C Belfiore and F. Oggier, “Lattice Codes Design for the Rayleigh Fading Wire-tap Channel,”Proc. IEEE International Conference on Communications Workshops, 2011, pp. 1-5.

[14] E. Arikan, “Channel Polarization: A Method for Constructing Capacity-achieving Codes for Symmetry Binary-input Memoryless Channels,”IEEE Transactions on Information Theory, vol. 55,no. 7, 2009, pp. 3051-3073.

[15] H. Mahdavifar and A. Vardy, “Achieving the Secrecy Capacity of Wiretap Channels Using Polar Codes,” IEEE Transactions on Information Theory,vol. 57, no. 10, 2011, pp. 6428 -6443.

[16] M. Andersson, V. Rathis, R. Thobaben, et al,“Nested Polar Codes for Wiretap and Relay Channels,” IEEE Communications Letters, vol. 14,no. 4, 2010, pp. 752-754.

[17] M. Yi, X. S Ji, K. Z Huang, et al, “A Method Based on Puncturing Polar Codes for Physical Layer Security,” Journal of Electronics & Information Technology, vol. 36, no. 12, 2014, pp. 2835-2841.

[18] L. Y. H Song, L. Xie, H. F Chen, et al, “A Feedback-based Secrecy Coding Scheme Using Polar Code over Wiretap Channels,” Proc. International Conference on Wireless Communications &Signal Processing, 2014, pp. 1-6.

[19] Y. Fountzoulas, A. Kosta, and N. Karystinosg,“Polar-code-based Security on the BSC-modeled HARQ in Fading,” Proc. International Conference on Telecommunications, 2016, pp. 1-5.

[20] B. Duo, P. Wang, Y. H Li, et al, “Secure Transmission for Relay-eavesdropper Channels Using Polar Coding,” Proc. IEEE International Conference on Communications, Sydney, 2014, pp.2197-2202.

[21] M. Andersson, R. F Schaefer, T. J Oechtering,et al, “Polar Coding for Bidirectional Broadcast Channels with Common and Confidential Messages,” International Symposium on Wireless Communication Systems, vol. 31, no. 9, 2011,pp. 1901-1908.

[22] M. F Zheng, M. X Tao, and W. Chen, “Polar Coding for Secure Transmission in MISO Fading Wiretap Channels,” 2014, pp. 1-7, http://arxiv.org/abs/1411.2463.

[23] Y. X Zhang, Z. Yang, A. J Liu, et al, “Secure Transmission over the Wiretap Channel Using Polar Codes and Artificial Noise,” IET Communications, vol. 11, no. 3, 2017, pp. 377-384.

[24] Y. X Zhang, A. J Liu, K. G Pan, et al, “A Practical Construction Method for Polar Codes,” IEEE Communications Letters, vol. 18, no. 11, 2014,pp. 1871-1874.

[25] K. Chen, K. Niu, and J. R Lin, “Practical Polar Code Construction over Parallel Channels,” IET Communications, vol. 7, no. 7, 2013, pp. 620-627.