Contract-Based Content Delivery in 5G Converged Networks

Xiaoyuan Lu, Yiqing Li, Xiaoying Gan,＊, Yanwei Xu, Jun Yao

1 School of Computer Science, Fudan University, Shanghai, China

2 Dept. of Electronics Engineering, Shanghai Jiao Tong University, Shanghai 200240, China

3 Engineering Research Center of Cyber Security Auditing and Monitoring, Ministry of Education, China

5 Philips Lighting Research, China

I. INTRODUCTION

The demands for multimedia contents have grown rapidly with the surge of mobile terminals such as smart phones and table PCs. It poses huge burdens on the network load as bandwidth resources are consumed tremendously.Recent studies have shown that the fast growing traffics will soon become significant problems on the cellular infrastructure and cause severe congestion in the near future [1]. In particular,it is difficult for CP to satisfy the users’ demand because of the hard network load burdens under traditional unicasting transmission mode.

Multi-mode communications generate development for different types of heterogeneous access networks such as mobile cellular networks and wireless sensor networks evolved into converged networks[2]. Djamal-Eeddine et al. [3] presents an overview of converged networks with their integration levels and impacts on networks structure. The emergency of converged network provides people an effective way to relieve network pressure. Converged network relieves heavy burden due to the limit of bandwidth, and further improves the coverage of network. A lot of papers have studied the advantages of 5G converged network [4-6]. In [1],using concept of content popularity, it proves that a broadcast and cellular converged network can significantly improve the network capacity.

LTE evolved multimedia broadcast multicast service (shorted as eMBMS), which is proposed by Kim et al. [7], is supposed to play a major role in releasing the burden of multime-dia content delivery in 5G converged networks.With the conventional broadcasting schemes,eMBMS implements synchronous transmission to multi-users through shared radio bandwidth.eMBMS enhancements will proceed with 5G standardisation definition to be started.

This paper proposes a contract-based content delivery scheme,generating incentives for users to employ broadcasting transmission.

Moving further, Louis et al. [8] implements a LTE hybrid unicast broadcast synchronization framework that allows internet service providers efficiency for broadcasting services while maintaining individualization services for users. CP can either apply unicasting network transmission to serve users, which can accurately meet the users’ individual requirements; or apply broadcasting network transmission to serve users, which can improve network transmission efficiency and save costs. However, it fails to inspire users’desire to purchase because of its linear pricing model. From the perspective of CP, it needs to explore a new business model to get the maximized profit. Nevertheless, all these works focus on resources allocation scheme but ignore the business interactions among market parties.

To emphasize the economic interactions in the market, we usually use contract theory to analyze the relationship among CP, ISP and users. Contract theory is an important brand of economics springing up in the last few decades,accurately described in P. Bolton and M. Dewatripont et al. [9]. It is widely used in solving resources allocation problem in cognitive wireless networks. AbdelRahman Eldosouky et al.[10] uses a contract-theoretic approach to solve the problem of resource allocation in critical infrastructure with asymmetric information.Bahareh Nazari et al. [11] presents a distributed power allocation and price assignment algorithm over cooperative wireless networks. All these studies adopt contract theory to motivate the market parties or improve the system performance. In addition to the resources allocation problem, Yuqing Li et al. [12] have adopted contract theory in the economic analysis for the interactions among CP, ISP and users, which can provide an incentive mechanism for the whole market. Despite all the implementations of converged network architecture, no works to our knowledge so far have analyzed converged networks from a network economics point of view, which is the motivation of our work.

In this paper, we use contract theory to analyze the interactions between CP and users.Our goal is to set a business model in 5G converged network that can motivate both CP and users. To this end, we propose a contract-based content delivery scheme. We divide users into different types by their preference and satisfaction for traffic, which comes from the impacts of unicasting and broadcasting transmission on users. CP can allocate different services to different types of users with different prices. In addition, we propose a threshold based popularity model to explore the impacts of unicasting and broadcasting on CP’s transmission cost. Based on the threshold popularity model, CP designs an optimal services-prices strategy to maximize its own profit. In the perspective of users, they choose the optimal services-prices packages to maximize their own utilities based on their types. In general, our main contributions can be summarized as follows:

● We propose a contract-based content delivery scheme to maximize CP’s profit in 5G converged networks with dual transmission modes. By exploiting users’ preference and satisfaction, as long as content popularity, the improvement in CP’s profit can be achieved.

● The optimal contract has been obtained,which incents users employing broadcasting transmission. In this way, constraints on Individual Rationality and Incentive Compatibility are satisfied.

● It is found that users’ preference can be formulated as a conditional probability of popularity threshold. Hereby, we can further improve CP’s profit by exploring the impact of popularity threshold.

The rest of this paper is organized as follows. In Sec. II, we set up the system model including business model and content popularity model to analyze the interactions between users and CP. Sec. III proposes the optimal contract by exploiting users’ preference. Sec. IV details how to exploit users’ satisfaction to obtain the optimal contract. Numerical results are given in Sec. V. Sec. VI concludes this paper.

II. SYSTEM MODEL

2.1 Business model

In this section, we analyze the market with three parties: a monopolistic CP, unicasting and broadcasting ISPs as two types of ISPs and a set of users M. CP rents the facilities from unicasting and broadcasting ISPs to provide the transmitting services for users. Users’ payment depends on their preference for unicasting or broadcasting transmission. The business relationship among CP, ISP and users is shown in figure 1. The direction of arrows shows the payment relationship between each role. Red block and grey block denote the preference for unicasting and broadcasting transmission mode respectively. The total preference is 1 for each user.Furthermore, the number in the block shows the percentage of traffic users will spend in broadcasting or unicasting transmission. It shows three different types of users in the figure. Specifically,the first type of users have average preference for two kinds of ISPs. The second type of users prefer unicasting network. Broadcasting network is more preferred by the third type of users.We suppose that the payment is proportional to traffic in unicasting network while it is proportional to the number of contents in broadcasting network. We do not consider the competitive relationship between these two types of ISPs.

2.2 Content popularity model

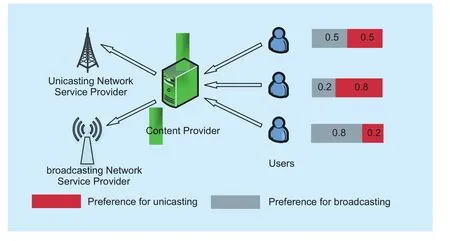
Fig. 1 Business model in converged network with unicasting and broadcasting coexistence

Users’ preference for specific contents can be described by content popularity model. Popularity means the demanded quantity of content.CP can set popularity threshold to decide the transmission mode of particular content. When the total number of contents N is large enough,the distribution can be regarded as continuous. We assume that the popularity satisfies a specific distribution. In [13], it demonstrates the popularity of video content satisfies Zipf distribution and follows pareto distribution by exploring the video content websites. Specifically, Osman et al. [14] demonstrates pareto distribution can fit the content popularity distribution well in the IPTV and video-on-demand(VoD) services analysis. In this section,we adopt pareto distribution to analyze the content popularity distribution.

First we need to rank the contents based on the popularity using content popularity function. The higher popularity, the higher ranking of the content. The probability density function of Pareto distribution is

We can get the cumulative density function:

where independent variable τ in Pareto distribution describes the ratio of contents with ranking higher than τ occupying the whole contents. It has scale of 0≤τ≤1. Dependent variable g()τ describes the demanded quantity of a specific content. The parameter γ is popularity index, describing the distribution tendency of content popularity.

It shows the content popularity probability density function when the whole number of contents N = 100 in figure 2. Popularity means the popularity probability density as g(β;γ).For example, when β=20, we can get

labeled in the figure. We describe marginal benefit as the number of users’ satisfied demand when a broadcast transmission content is added. We find it decrease when β increases,which is one of the important reasons why the CP needs to balance the ratio of unicasting and broadcasting transmission.

III. OPTIMAL CONTRACT IN USERS’PREFERENCE MODEL

In this section, we analyze the performance of converged networks using the contract theory under the continuous model. CP constructs the contract relationship with users to sell the traffic based on the principle of maximizing self-benefits. We model this situation to get a solution and do the numerical analysis.

The parameters in the business model are shown in Table 1.

3.1 Problem formulation

For users in converged network, we find that different users have different habits when using the unicasting or broadcasting network. We divide users into different types by their preference for unicasting or broadcasting services.We denote the types of users θ as the ratio of broadcast traffic over the whole traffic. For example, θ = 0.2 represents that the user transmits 20% of traffic by broadcasting network and 80% of traffic by unicasting network.

For the definition of user’s utility function,we should consider two factors:

1) The relationship between user’s demand and benefit is nonlinear. Specifically, it is concave. In general, user gains higher benefit for requisite content traffic and reduces his benefit for unnecessary traffic. Furthermore, the marginal benefit decrease with content traffic increasing.

2) User has different gains over unicasting services and broadcasting services, which is decided by the transmission features of unicast and broadcast networks. Broadcast network buffers user’s video to the cache,where user can watch the video without delay although the hit ratio is low. In unicast

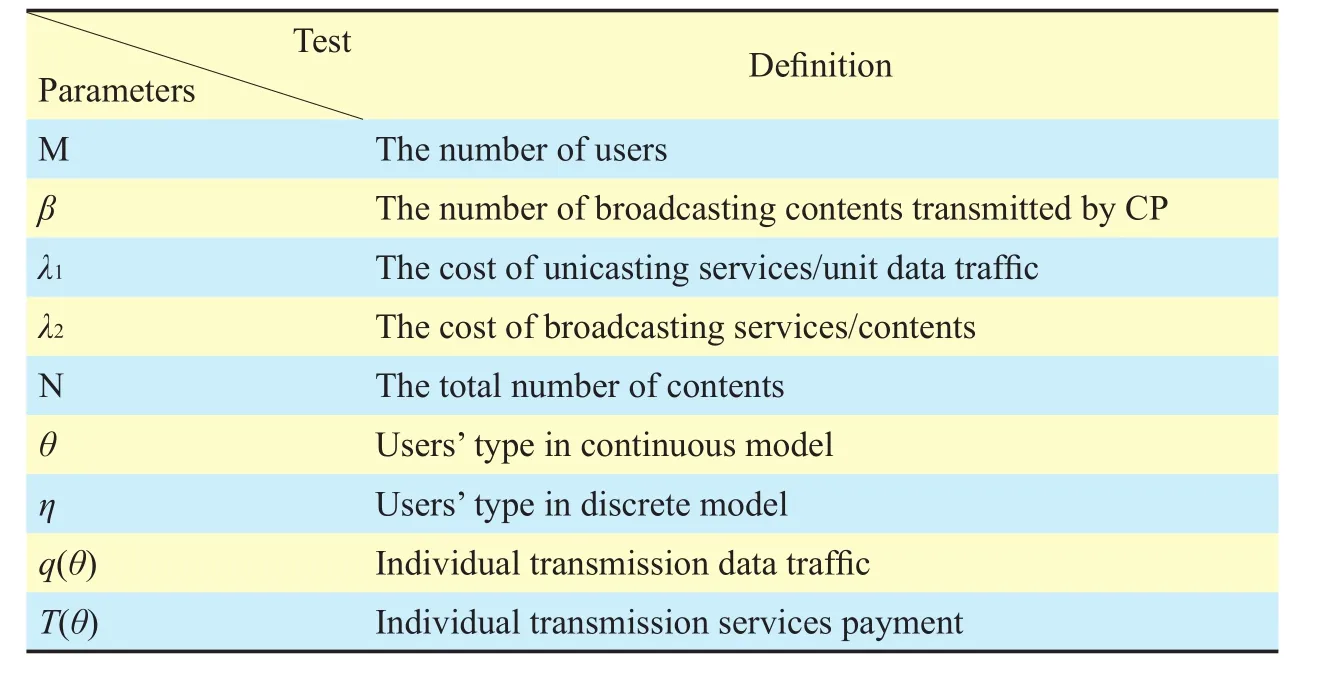
Table I The parameters in the model

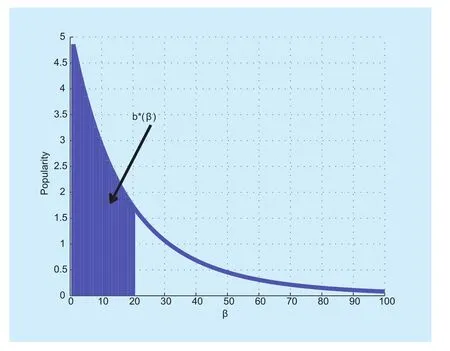
Fig. 2 The probability density function of content popularity

network, it has high hit ratio but user will suffer long delay while watching the video.

Based on these two factors, we choose logarithmic function to model the utility function for users.

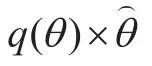
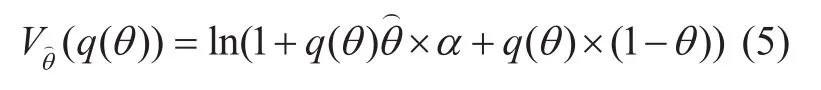
where α represents the utilization index of broadcasting services relative to unicasting services. We assume that α＞1. It means that the utility of user under broadcast transmission will be larger than that under unicasting transmission when broadcasting transmission hits.Based on (5), we can have the utility function for users as

We assume that different types of users satisfy a certain statistical distribution f(θ).According to the content popularity model,we can solve the users’ distribution function based on the users’ broadcasting transmission demand b*(β). Actually, it can be proved that the users’ distribution function satisfies b(b*(β),D), where D is the average number of demanded contents for a single user. We use Poisson distribution model to construct the users’ distribution function. The binomial distribution b(b*(β),D) can be approximated as Poisson distribution of (7).

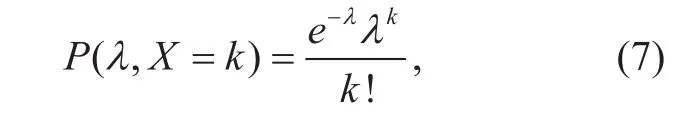
According to Poisson distribution, we define the users’ distribution function as

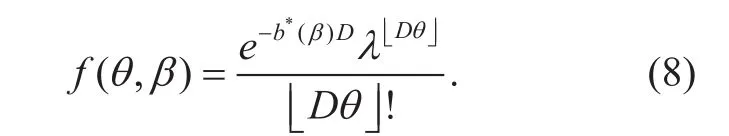
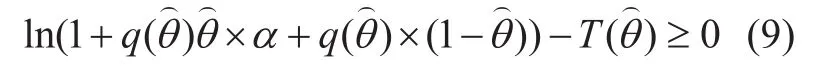
In the business model, CP needs to construct the contract as traffic services and price(q(θ),T(θ)). Meanwhile, CP chooses the number of broadcast transmission content β.We define the profit function of CP as:

As for the cost of CP, it includes three parts.The unicasting services cost is

The broadcasting services cost is

where λ1and λ2are defined in Table. 1. The last part is the constant services cost as C0.Add three parts up and we get the cost function of CP as:

Thus, we have the utility function of CP as

Take (11) and (14) into (15). We can get the optimal problem as

For solving (16), we firstly get the optimal contract strategy (q(θ),T(θ)) for CP that maximizes their own benefit. Secondly, we get the broadcast transmission content number β corresponded with the optimal contract.

3.2 Optimal contract analysis

In this section, we solve the problem of optimal contract designed with incomplete information. First we simplify the IR constraint.

Lemma 1.In the optimization problem(16), we assume that IC condition is satisfied.Thus, IR condition can be replaced by

Proof: Assume for any parametersthey satisfy. According to IC condition, we have

It represents the utility function of user is a increasing function. Therefore, for anywhen (21) is satisfied as

the IR condition can be achieved.

We adopt Spence-Mirrlees Single Crossing Condition to analyze the IC condition.

Definition 3. Spence-Mirrlees Single-Crossing Condition: The users’ utility function satisfies single crossing condition if and only if (22) is satisfied

The single crossing condition represents that users with higher θ have higher profit than those with lower θ. For the users’ utility function as (6), we have

It means that the users’ utility function satisfies the single crossing condition. Thus, we can use Spence-Mirrlees Single Crossing Condition to simplify the IC condition.

Lemma 2.Once the users’ utility function satisfies the single crossing condition, the IC condition can be replaced by the following two constraints:

1) Monotonicity constraint

● Local incentive compatibility constraint

The proof of lemma 2 is in the appendix.

Under the IC and IR conditions, we first analyze the optimal problem under other constraints neglecting. Secondly, we consider thecondition. We define the utility function of θ type of users selecting the corresponded contract (q(θ),T(θ)) as

According to envelop theorem, we can get

Integrate (27) and assign W(0)=0. We have

Thus, we can get the contract price T()θ as

which indicates the functional relationship between q()θ and T()θ. Bring (29) into UCP()β and do the integration, the CP’s utility function becomes (30) shown in the bottom at this page.

Differentiate (30), we can get the optimal q()θ for maximizing the CP’s benefit

where

Based on (29) and (31), we have the optimal contract as (q(θ),T(θ)). It is noteworthy that β is settled in the above analysis. We do not give out a closed form solution of β when the CP reaches the maximized benefits because of the complexity of the formulas. But we will give out a numerical solution for β in the simulation.

In the above discussion, we assume that q′(θ)≥ 0 and get a closed optimal solution in the contract model. But for q()θ, it may not be monotonic for its actual result. It means that in a finite interval [ai,bi] we have q′(θ)＜ 0. We can use the following algorithm to adjust q(θ).

b) Adjust q()θ to

It is easy to know the relationship between data traffic and the price is nonlinear in this contract model. Therefore, we adopt a linear pricing model to do the comparison, analyzing the effect that different pricing models will bring to the CP on the benefit.

We assume that CP adopts the price model based on traffic plus constant price as

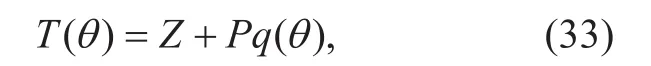
where P is unit-price to the traffic, Pq()θ is the pricing part of the traffic and Z is the constant price that users pay monthly to CP.Therefore, the optimal problem is

where

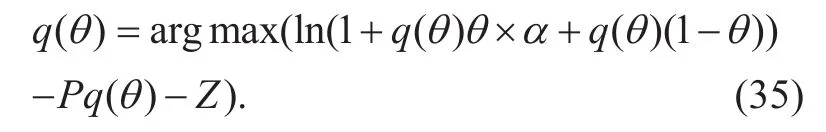
It satisfies IR condition as

which turns into an equation on the optimal solution. q()θ still satisfies (31). Meanwhile,P satisfies

or

We can get Z as

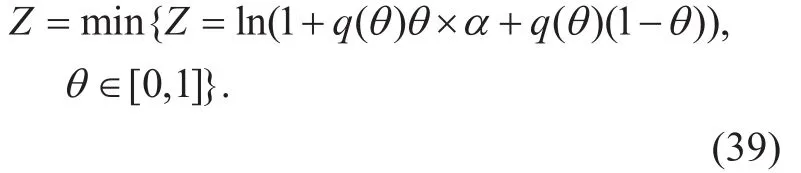
Thus, the benefit of CP is

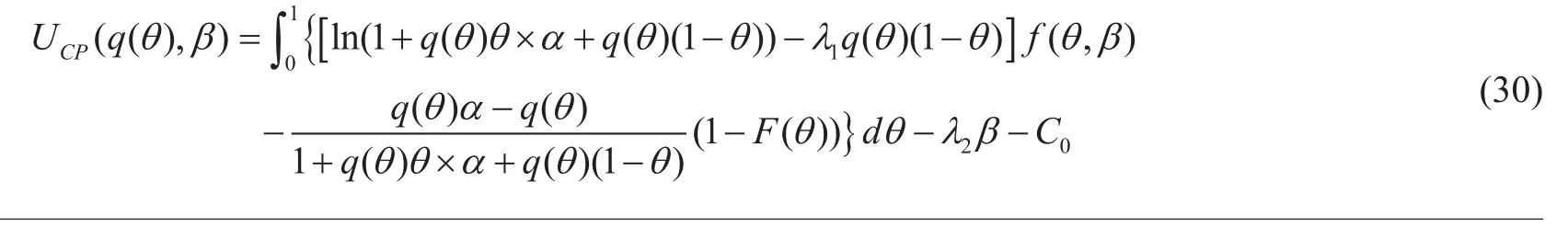
Taking the formulation of P as (37) or (38)into (40), UCPturns into

Differentiate (41) by β, we get

which indicates that the benefit of CP decreases with bigger β. It demonstrates that the cost for unicasting services counteracts CP’s profit apart from constant charging. Therefore, CP’s profit reduces due to the increasing cost for broadcasting services with bigger β.

In the simulation section, we give out the comparison results of linear pricing model and nonlinear model.

IV. OPTIMAL CONTRACT IN USERS’SATISFACTION MODEL

In this section, we take the users’ satisfaction into account based on the preference model using discrete contract model. We divide users into different types based on their satisfaction under certain users’ preference.

4.1 Problem formulation

Based on the users’ demand for data traffic,denoted as η, we divided users into different types. Users have higher satisfaction for traffic with bigger η. We assume that users have lower utilities with low satisfaction under the same traffic consumption. Conversely, users have higher utilities with higher satisfaction.The users’ utility function is

where qirepresents the contract traffic of i type of users and Tiis the bundled price. ηi∈[0,1] and it increases with i. α represents the utility index.

Definition 4. IR Constraint: When selecting corresponded contract (qi,Ti), ηitype of users satisfies

It represents (qi,Ti), ηitype of users get non negative profits selecting the corresponded contract.

Definition 5.IC Constraint: When ηitype of users select the corresponded contract(qi,Ti), for all ηi,ηj∈[0,1], it satisfies

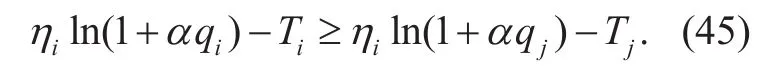
IC condition represents ηitype of users can achieve their maximized profits selecting contract

We can get the utility function of CP as(15). Although we use different standard to divide users, the cost of CP is the same. Specifically, in satisfaction model, the users’ distribution is certain. The cost function of CP in satisfaction model is:

where I represents the number of all the types of users, Mirepresents the users’ number of i type of users and b*()β is defined as formula (3).The profit function is to add the total users’ profit up according to their types. Thus, we have

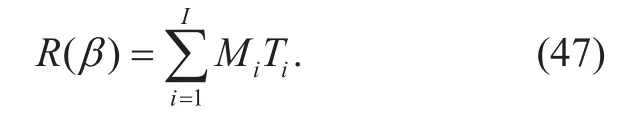
Bring (46) and (47) into (15), the utility function of CP is

We have the optimal contract problem as

4.2 Optimal contract analysis

In this section, we solve the optimal problem as formula (49) shown.

First to satisfy the IR condition, we have

For the IC constraint, we use some lemmas to do the simplification in order to solve the optimal problem.

Lemma 3. Increasing Preference (IP) Property: For ηi≥ηjand qi≥qj, the users’ profit function satisfies

Meanwhile, the marginal profit on q of users increases with η increasing.

Lemma 4.Local Downstream Incentive Compatibility: Once local downstream IC condition is satisfied, that is to satisfy

For any i≥j, IC condition is satisfied as

Similarly, we can get the property of local upstream IC condition.

Lemma 5. Local Upstream Incentive Compatibility: Once local upstream IC condition is satisfied, that is to satisfy

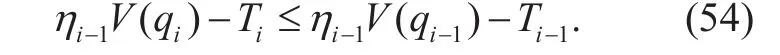
For any i≥j, IC condition is satisfied as

According to lemma 4 and lemma 5, we can simplify IC condition into local upstream IC condition and local downstream condition.In the following analysis, we only consider the local downstream IC condition. It is similar under local upstream IC condition.

Lemma 6.Optimal Solution Condition:When CP has achieved the maximized profit,local downstream IC condition turns to

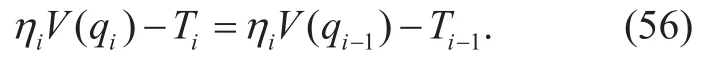
Therefore, we can simplify the optimal contract problem as formula (49) to (57)

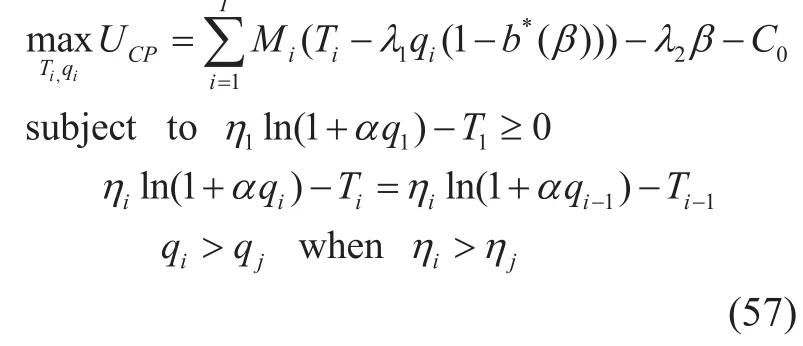
Based on the formula (56), we can have Tiunder ∀i∈{1,...I} as

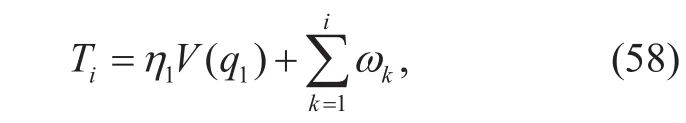
where ω is

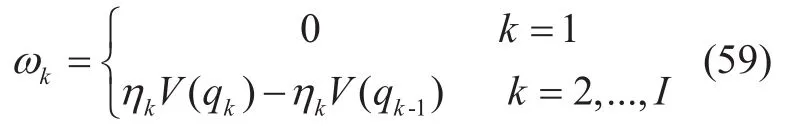
Bring formula (58) into (48), we have

where

Thus, we can get the corresponded traffic qiwhen CP achieves the maximized profits

Combining (63) with (58), we can get the formula of Ti.

However, we do not consider the monotonicity of qi. It means that in the result that we get, it may exist a situation of qi＜qjwhen ηi＞ηj. To solve this problem, we use a lemma in [15].

Lemma 7.Maximum Lemma: Suggest X1(x),...,Xn(x) are convex functions about x.The optimal solution xi=argmaxXi(x ) maximizing Xi(x) must satisfy x1≥x2≥...≥xn.Therefore, the optimal solution x~ifor formula(64) satisfyingmust have

We adopt lemma 7 to adjust qiwhen it does not satisfy the constraint condition. The adjustment algorithm is as

1) Get the optimal solution qibased on formula (63).

2) When qidoesn’t satisfy constraint condition, finding the intervalwhich doesn’t satisfy the monotonic constraints. For ∀k∈ {i,i+1,...,j} , assign

3) Repeat the step 2 until all the qisatisfy the monotonic constraints condition that is it has qi＞qjwhen ηi＞ηj.

According the above algorithm, we can get the optimal solutionsatisfying the mono-tonic condition. The solution can be obtained in time complexity of O(I2).

V. NUMERICAL RESULTS

In this section we give out the numerical results of optimal contract. The parameters are set as Table. 2. We have 1000 users and 100 contents in our model. Note that the number of broadcasting contents β is given as 10 in optimal contract analysis. Intuitively, the cost of broadcasting services is much higher than that of unicasting services and therefore, we set λ1=0.005 and λ2=5. The content popularity index is γ=5. To explore the price that users pay for unit traffic service, we define the unit traffic price as the contract price T()θ divided by data traffic q()θ

5.1 Users’ preference model

As shown in figure 3, we illustrate the results of optimal contract item (q(θ),T(θ)) in terms of users’ types. Meanwhile, we give out the results under different users’ utilization of broadcasting transmission relative to unicasting transmission. Specifically, α＜1 describes that users can obtain higher utilities when watching videos in unicasting transmission when α＞1 indicates higher broadcasting utilities that users can obtain. In figure 3(a), firstly we consider the situation α＞1, it shows that the contract traffic q()θ increases with θ increasing. CP will allocate more traffic to those users with more broadcasting transmission preference.Furthermore, we can see that once α grows up,the traffic approaches 0 when θ is small. In this case, CP even will not allocate data traffic to users with lower θ. However, in the situation of α＜1, CP provide less data traffic to higher θ users since users’ utilities decrease when their preference for broadcasting transmission mode increases. In figure 3(b), it represents the relationship between contract price T()θ and users’ type θ. T()θ increases with θ increasing under α＜1. Combined with figure 3(a),it means that higher contract traffic q()θ corresponds with higher prices T(θ) for users and vice versa. Meanwhile, in the case of α＞1,due to the higher utilities for users and lower cost for CP, when α increases, contract price T(θ) increases as well.

The relationship between users’ types and unit traffic price are shown in figure 4. Firstly,we consider the situation under α＞1. For users with higher θ, CP charges them with low price. CP will get more profits when the number of users preferring broadcasting transmission is increasing. Therefore, the unit traffic price decreases to inspire users to get more preference for broadcasting transmission.Meanwhile, unit traffic prices increases with α. In this case, users can get more utilities introduced by larger α. Thus, with guaranteed positive utilities, they can accept higher price.As for the situation under α＜1, the unit traffic price is nearly 0 when θ is low since CP provides large amount of data traffic to users.Moreover, the unit traffic price firstly increase and then decrease with the increase of θ.

We give out the numerical results of two pricing models as optimal contract pricing model and a linear pricing model based on traffic plus constant price as (33) in figure 5. It shows the relationship between broadcasting contents number β and the profits of CP. We can see that the optimal pricing model has the best profit gaining for CP. In the optimal contact pricing model,when β is small, the profit of CP monotonically increases with low speed. Because in this case,the number of satisfied broadcasting transmission demands of users is increasing. When β is too high, the profit of CP is decreasing for thelarge renting cost for broadcasting services.

Table II Parameters setting in the model

Fig. 3 Optimal contract in terms of users’ preference model

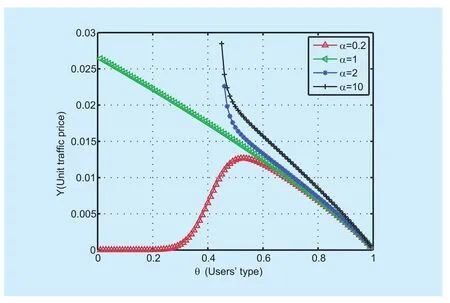
Fig. 4 Unit traffic price in users’ preference model

5.2 Users’ satisfaction model

We use binomial distribution to model the distribution of users with probability p. Specifically, lower p means users are mainly distributed at the area with lower η and vice versa. Figure 6 shows the results of contract item (q(η),T(η))in terms of users’ type η in users’ satisfaction model. Figure 6(a) shows the users contract traffic lines under different users’ distribution.We can see that traffic increases with η. Meanwhile, with higher p, the optimal strategy of CP will not allocate any traffic to those with lower η. In figure 6(b), it shows the lines of price of contract under different users’ distribution. We can see that T()η increases with q()η. The price for users with higher η is higher than those with lower η. Because we know that users with higher η have high utilities under that same data traffic as (43). Therefore, CP can get more profits by increasing the price of traffic.

We illustrate the relationship between unit traffic price and users’ types under different users’ distribution in figure 7. We can see that users with higher η can be charged with low unit traffic price under the same p. Therefore,it can inspire users with high satisfaction. Due to the higher utilities for users and lower cost for CP, unit traffic price for users with higher p, is higher than that for users with lower p.

We consider the users’ number on unit bandwidth to analyze the communication performance gain under the broadcasting and unicasting converged networks scenario. In figure 1, it shows that when users have higher preference for broadcasting services, users’ number on unit bandwidth increases, which indicates network with more broadcasting resources is more able to provide content delivery services to a large volume of users. Moreover, it shows a sharp rise with bigger θ.

In this paper, we propose a contract-based content delivery scheme to maximize CP’s profit in 5G converged networks. To model the utility of CP, we exploit users’ preference and satisfaction as long as content popularity.From the analysis, we can obtain the optimal contract that maximizes CP’s profits. We can see from the numerical results that CP is able to improve its profit by incenting users preference for broadcasting. In addition, a proper selection of popularity threshold can help CP further improve its profit. Users with higher satisfaction enjoy lower unit traffic price, motivating users demand for more data traffic. Furthermore, CP can get the maximized profits with nonlinear pricing model. As for the future work, we can take the relationship between broadcasting and unicasting ISPs into account. The prediction of users’ distribution can be another consideration.

ACKNOWLEDGEMENT

This paper was partly supported by NSFC Grant(No. 61672342, No. 61671478, No. 61572319,No. 61532012, No. 61325012, No. 91438115),with Science & Technology Innovation Program of Shanghai Grant (No. 17511105103),National Key Scientific Research Project under Grant (No. 2017YFB0803200) and Natural Science Foundation of Shanghai under Grant (No.14ZR1427700).

Appendix

In order to prove lemma 2, we should first prove that under IC condition, formula (24)and (25) is true; then prove that if formula(24) and (25) is true, IC condition is true.

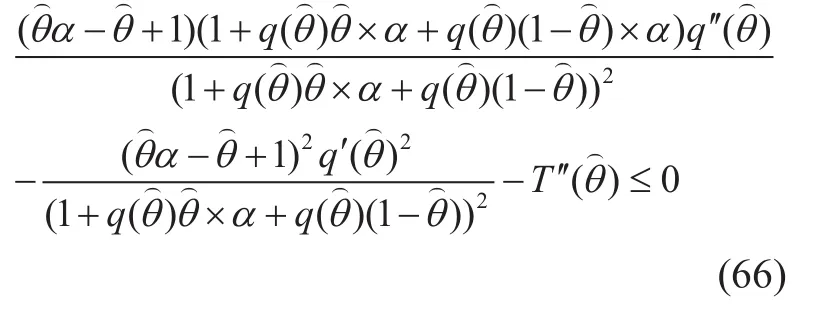
Fig. 5 Profit of CP in users’ preference model

Fig. 6 Optimal contract in terms of users’ satisfaction model

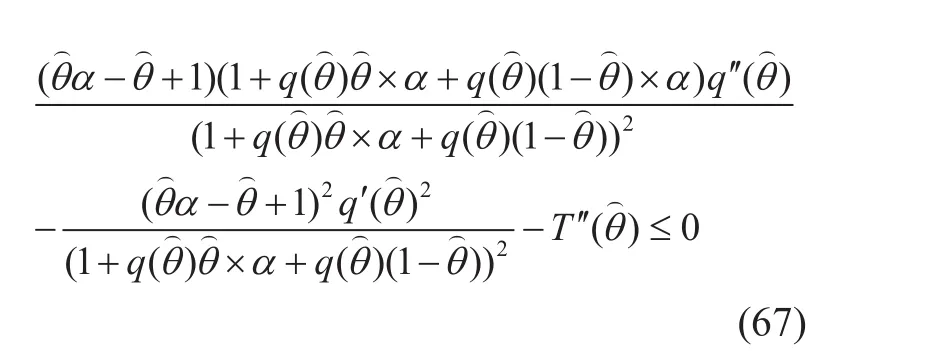
(66) is the local incentive compatibility constraint. We further derive the derivative ofon (66), and get

Fig. 7 Unit traffic price in users’ satisfaction model

Fig. 8 Bandwidth consumption of the network, N = 100

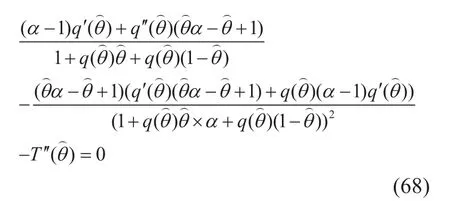
Compare (68) and (67), we can obtain the monotonic constrain of q(θ)

Rewrite (70) as a form of integration, and we get

According to monotonic constraint, we have q′(x)≥ 0. Combining it with Single-Crossing Condition, we have that for arbitrary θ~＞θ,and the following equation holds

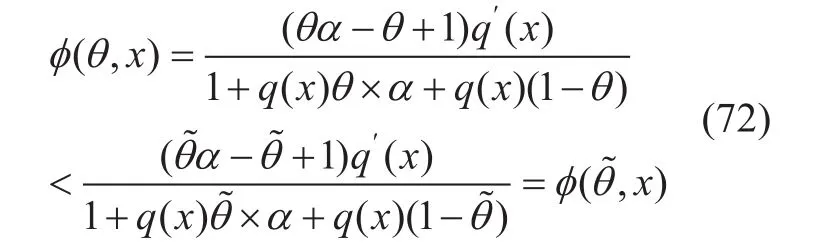
That is to say, φ(θ,x) is an increasing function about θ. Combining with local incentive compatibility constraint as (25), we have

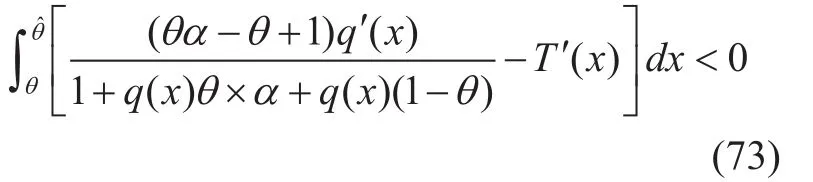
Obviously, (73) contradicts to (71). Thus,the assumption earlier is wrong.

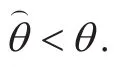
[1] K. Wang, Z. Chen, and H. Liu, “Push-based wireless converged networks for massive multimedia content delivery,” IEEE Trans- actions on Wireless Communications, vol. 13, no. 5, pp.2894– 2905, 2014.

[2] J. Zhang, L. Shan, H. Hu, and Y. Yang, “Mobile cellular networks and wireless sensor networks:toward convergence,” IEEE Wireless Magazine,vol. 50, pp. 164–169, 2012.

[3] D.-E. Meddour, U. Javaid, N. Bihannic, T. Rasheed,and R. Boutaba, “Completing the convergence puzzle: a survey and a roadmap,” IEEE Wireless Communications, vol. 16, pp. 86–96, 2009.

[4] S. Y. Baek, Y.-J. Hong, and D. K. Sung, “Adaptive transmission scheme for mixed multicast and unicast traffi c in cellular sys- tems,” IEEE Transactions on Wireless Communications, vol. 13, no.5, pp. 2899–2908, 2014.

[5] D. Lee, W. Kim, B. Bae, H. Lim, and J. So, “Converged archi- tecture for broadcast and multicast services in heterogeneous network,” Proc.16th International Conference on Advanced Communication Technology, pp. 141–145, 2014.

[6] L. Shi, K. W. Sung, and J. Zander, “Future tv content delivery over cellular networks from urban to rural environments,” IEEE Transactions on Wireless Communications, vol. 14, no. 11, pp.6177–6187, 2015.

[7] Kim and Dong-Hoi, “Adaptive handover scheme for evolved multimedia broadcast multicast services in long-term evolution networks,” IET Communications, vol. 8, no. 16, pp. 2933–2942, 2014.

[8] L. Christodoulou, O. Abdul-Hameed, and A. M.Kondoz, “To- ward an lte hybrid unicast broadcast content delivery frame- work,” IEEE Transactions on Broadcasting, no. 99, pp. 1–17, 2017.

[9] P. Bolton and M. Dewatripont, Contract Theory.The MIT Press, 2005.

[10] A. Eldosouky, W. Saad, C. Kamhoua, and K. Kwiat, “Contract- theoretic resource allocation for critical infrastructure protec- tion,” Proc. IEEE Global Communications Conference (GLOBECOM), pp. 1–6, 2015.

[11] B. Nazari and A. Jamalipour, “Contract-auction based distribut- ed resource allocation for cooperative communications,” IET Communications, vol. 10, no. 9, pp. 1087–1095, 2016.

[12] Y. Li, J. Zhang, X. Gan, L. Fu, H. Yu, and X. Wang,“A contract-based incentive mechanism for traffic offloading over delay tolerant networks,”IEEE Transactions on Wireless Com- munications,vol. 15, no. 8, pp. 5314–5327, 2016.

[13] M. Cha, H. Kwak, P. Rodriguez, Y.-Y. Ahn, and S.Moon, “Analyzing the video popularity characteristics of large-scale user generated content systems,” Networking, IEEE/ACM Trans- actions on, vol. 17, no. 5, pp. 1357–1370, 2009.

[14] Osman, N. El-Gorashi, T. Elmirghani, and J.M.H,“The impact of content popularity distribution on energy efficient caching,” Proc. Transparent Optical Networks (ICTON), 2013 15th Inter- national Conference on, pp. 1–6, 2013.

[15] L. Gao, X. Wang, Y. Xu, and Q. Zhang, “Spectrum trading in cognitive radio networks: A contract-theoretic modeling ap- proach,” Selected Areas in Communications, IEEE Journal on, vol.29, no. 4, pp. 843–855, 2011.