初中教学中的数形结合思想

刘杰

数形结合的思想方法，就是把数、式与图形结合起来，利用问题中的数量关系和几何图形解决实际问题，数形结合是数学教学中重要的数学思想。如何让学生在学习数学中形成数形结合的意识，形成数形结合的思想方法，从某种程度上来说可以决定我们数学教学的成败。

一、数形结合是数学教学中十分重要的思想方法

“数形结合思想就是从几何直观的角度，利用几何图形的性质研究数量关系，寻求代数问题的解决方法（即以形助数），或利用数量关系来研究几何图形的性质，解决几何问题（即以数助形）的一种数学思想”。数形结合的实质就是“就是将抽象的语言和直观的图形（几何性质）结合起来，使抽象思维和形象思维结合起来，实现抽象概念与具体形象的联系和转化”。在解决有关问题时，数形结合方法所表现出来的思路上的灵活、过程上的简便、方法上的多样化是一目了然的。

初中是学生数学思维品质萌发及形成的初期，在各年级各阶段，适当地渗透、运用数形结合思想，对学生的形象思维与抽象思维的形成、融合，以及对学生的逻辑思维的深化都有着重要的意义；同时对学习数学知识，深入浅出地、直观地揭示知识的内涵，使抽象的数学知识变得形象生动、直观具体，使学生感到易学、乐学，激发其求知欲也都有重要意义。因此，数形结合解题方法是初中生应掌握的一种重要思想方法，因而我们在平时的教学工作中，必须认真细致地运用和落实数形结合的思想方法，以逐步提高学生的数学思维水平和形象思维能力。

二、“数缺形，不直观；形缺数。难入微”

可见数形结合的思想，就是研究数学的一种重要的思想方法，它是指把代数的精确刻画与几何的形象直观相统一，将抽象思维与形象直观相结合的一种思想方法。它能让复杂的数学问题简单化。

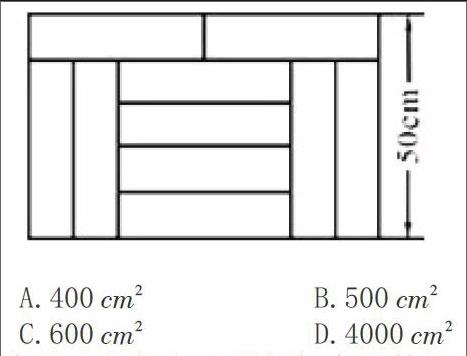
例如右图，宽为50cm的长方形形图案由10个完全相同的小长方形拼成，其中一个小长方形的面积为（ ）。

分析：根据图中蕴含的长方形的长与宽的数量关系，可列出长与宽关系的二元一次方程组，进而求出每一个小长方形的长宽和面积。

解：设小长方形的长为xcm，宽为ycm，

几何图形在数学中所具有的最大的优势就是直观易懂，所以在谈到“数形结合”思想时，就更偏好于“以形助数”的方法，利用几何图形解决相关不易求解的代数问题。几何图形直观的运用于代数中主要体现在几个方面：①利用相关的几何图形帮助记忆代数公式，例如：完全平方公式与平方差公式；②利用数轴及平面直角坐标系将一些代数表达式赋予几何意义，通过构造几何图形，进而帮助求解相关的代数问题，或者简化相关的代数运算。

三、逐步渗透数形结合的思想，培养学生用数形结合分析问题的意识。提高解决问题的能力

每个学生在日常生活中都具有一定的图形知识，如绳子和绳子上的结、刻度尺与它上面的刻度，温度计与其上面的温度，我们每天走过的路线可以看作是一条直线，教室里每个学生的坐位等。数学源于生活，合理利用生活中数学资源，把生活中的形与数相结合迁移到数学中来，在教学中进行数学数形结合思想的渗透，利用教材提供的每一个机会，把握好渗透的契机。如数与数轴，一对有序实数与平面直角坐标系，一元一次不等式的解集与一次函数的图像，二元一次方程组的解与一次函数图像之间的关系，一元二次方程与二次函数图像的关系等，都是渗透数形结合思想的很好机会。

如教学七年级数学有理数和八年级实数这些内容时，利用数形结合来进行教学会取得可喜的教学效果。直线是由無数个点组成的集合，实数包括正实数、零、负实数也有无数个，因为它们的这个共陛所以用直线上无数个点来表示实数，这时就把一条直线规定了原点、正方向和单位长度，把这条直线就叫做数轴。建立了数与直线上的点的结合。即：数轴上的每个点都表示一个实数，每个实数都能在数轴上找到表示它的点，建立了实数与数轴上的点的一一对应关系，由此让学生进一步理解了相反数、绝对值的几何意义。建立数轴后及时引导学生利用数轴来进行有理数的比较大小，学生通过观察、分析、归纳总结得出结论：通常规定右边为正方向时，在数轴上的两个数，右边的总大于左边的，正数大于零，零大于负数。让学生理解数形结合思想在解决问题中的应用。为下面进一步学习数形结合思想奠定基础。

结合探索规律和生活中的实际问题，反复渗透，强化数学中的数形结合思想，使学生逐步形成数学学习中的数形结合的意识，并能在应用数形结合思想的时候注意一些基本原则，如是由形确定数还是由数确定形，在探索规律的过程中应该遵循由特殊到一般的思路进行，从而归纳总结出一般性的结论。

四、学习数形结合思想，化抽象为具体，提高学生学习的兴趣

在教学中渗透数形结合思想时，应让学生了解，所谓数形结合就是找准数与形的契合点，根据对象的属性，将数与形巧妙地结合起来，有效地相互转化，就成为解决问题的关键所在。

数形结合的结合思想主要体现在以下几种：①用方程、不等式或函数解决有关几何量的问题；②用几何图形或函数图像解决有关方程或函数的问题；③解决一些与函数有关的代数、几何综合性问题；④以图像形式呈现信息的应用性问题。

数形结合思想的应用往往能使一些复杂的问题变得直观，解题思路非常的清晰，步骤非常的明了，将抽象的数学形象化。另一方面在学生学习过程中，可以激发学生学习数学的兴趣。

数形结合的思想在教学中的应用，一方面，借助于图形的性质可以将许多抽象的数学概念和数量关系形象化、简单化，给人以直觉的启示。另一方面，将图形问题转化为代数问题，以获得精确的结论。这种“数”与“形”的信息转换，相互渗透，不仅可以使一些题目的解决简捷明快，同时还可以大大开拓我们的解题思路，为研究和探求数学问题开辟了一条重要的途径。

数形结合的思想是一种高层次的思维活动，是数学发现过程中的一种创造性思维。“观察、归纳、猜想”型探索性问题，使学生以“数学家”的角色，置身于猜想、发现的情境之中，这类问题对开拓思维，培养创新意识和探索能力大有裨益。