精算方法在商业银行信贷风险管理之中的应用研究

曹杰雯

商业银行是金融机构体系的重要组成部分，不仅经营存贷款业务，承担融资功能，同时还承担着支付清算等多项功能。经济的快速发展造成了我国经济环境的日益复杂和经济发展的不确定性，银行作为最重要的金融中介机构，承受着国内经济发展不平衡、金融市场不发达、利率还没有市场化等很多的不利因素。再加上我国银行业本身的管理系统和法律体系运行的时间还很短，很多地方不完善，导致信用风险在银行内部不断积累，成为我国商业银行现在面临的最大危机。

与发达国家银行体系长达三四百年的发展相比，我国商业银行各种控制系统的建立时间还很短。目前国内银行业不良贷款问题的不断凸现更有着与国际银行业不同的特定背景因素，主要体现为国有商业银行特定的制度性风险和结构性风险问题。

一、现行商业银行信贷风险管理方法评析

当前国际上使用最多的几个模型是 Credit Metries、KMV、Credit Risk+、Portfolio View模型等。但是由于信用风险自身存在着诸如分布不对称以及数据匮乏等问题，各国银行界对信贷风险量化方法也尚未达成共识。

KMV模型的优势是计算预期违约概率。KMV模型并不是通过分析最初的信用评级得出违约概率的，而是以期权定价理论为基础，通过分析企业自身的财务数据来预测贷款人的违约概率的。由于KMV模型仅仅通过贷款人的财务结构以及贷款人资产的当前现值来推导预期违约率，所以它没有对信用评级以及未来信用评级变化情况作任何假设，这是KMV模型与其他模型的区别。

KMV模型也存在着一些缺陷：

（1）要对资产收益的分布用正态分布进行假设才能构造理论上的预期违约率；

（2）难以预测与度量资料不全的公司或个人；

（3）KMV模型不适用于动态的分析，因此不能用于分析正处于兼并重组过程中的企业。

Credit Metrics模型是通过使用贷款信用VaR作计量工具，其结果：市场行情不好的年代，银行贷款会遭受巨大损失，因为贷款并不像股票和债券那样可以在公共市场进行交易，所以我们没有办法直观的看到他的市场波动性与市场价值，如果我们要计算贷款损失的可能性，只有通过了解贷款其本人的信用积分或者信用评级，从而在下一个时间段尽可能降低违约贷款的可能性，把违约贷款的损失率降到最低。

与其他模型相比，Credit Metrics的突出特点在于模型输出的结果不是贷款人和交易对手的违约概率，而是确定置信度下的信用的风险价值VaR的值。

但是Credit Metrics模型仍存在一些不足之处：

（1）模型最大的不足在于假设信用风险和市场风险是相互独立的，贷款唯一的不确定性就是贷款人的信用等级发生变化；

（2）模型做出了很多假定；

（3）该模型还假定，贷款信用风险的VaR在不同的行业周期里都是不变的。

Credit Risk+是CSFP公司开发出来并于1997年底公开的一个新型信贷风险评价模型。该模型的主导思想是：“损失取决于灾难发生的频率和灾难发生时造成的破坏程度”，这是源于保险精算学的。贷款发生违约的频率和严重程度是确定贷款组合的损失分布的重要因素，因此Credit Risk+模型就是根据这种思想计算来债券或贷款组合的损失分布，从而对贷款组合进行风险分析和度量。

Credit Risk+模型的计算过程和结果非常有效，是因为其使用泊松过程刻画贷款违约，债务人的边际风险分布等数据比较容易获得，由于该模型给出的损失分布是一个表达式，所以所需要的估计数据很少，最后由于给出的是损失的分布函数，所以可以更加直观的看到损失存在的各种特征，从而使得对风险管理更加直接。因此Credit Risk+模型最大的优点是简单易用、结果容易理解。Credit Risk+系统可以根据成不同地区、不同部门、不同时限的个体得到不同的风险损失分布。

但该模型同样存在不足：Credit Risk+模型在方法上和其他模型一样没有考虑市場风险，同时贷款人信用级别的变动情况也被忽略了，也就是说该模型假设了风险对于每个债务人是固定的，而且在评估期间他们的信用级别不会发生变动，只使用远期利率变动来刻画模型风险。甚至在很多情况下，将模型简化，违约概率可以由几种随机背景因子计算直接得到，也就是说违约率是常数。这大大削弱了模型精度。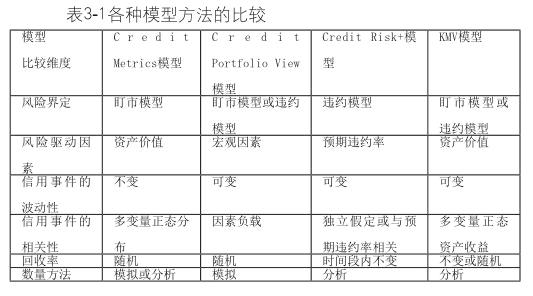

二、精算方法在风险管理中的优点

精算学之所以能够度量银行违约风险，主要以下两大原因：首先是精算学之所以能为保险公司提供决策依据和管理方法，是因为它在现代数学和统计学为基础上，量化分析和研究了保险经营中的各项损失风险。保险公司之所以能在激烈竞争的市场环境中得以生存并且发展离不开保险精算的重要支持。精算学最早是在人寿保险的费率厘定的时候使用的，现在精算学已不仅限于寿险，在非寿险、投资、银行等金融领域也有着很广泛的应用。其次，精算模型可用于研究银行违约风险是因为银行贷款也存在这未来随机出现的违约所造成损失的可能。银行之所以为面对贷款人的违约风险，是因为银行在将资金贷出去时并不能确定借款人一定能够还款，而这个违约风险将造成的损失也是一个随机变量。银行一方面需要度量违约损失，另一方面还要对贷款质量进行控制，降低违约风险发生的几率，并且要提留准备金对风险进行防范。

精算方法还有一个比较独特的优势就在于它对目标值的统计、推断和预测都是建立在过去自身的有效记录上的，因此运用精算方法可以适合不同目标范围和对象使得在进行信贷风险评估时可以根据不同的评估主体而得出不同的模型参数，从而使得精算方法的使用更加贴近实际，真实的反应评估主体各项特征。

总而言之，精算模型是比较适合于研究这类对风险计量与定价。

三、精算方法在信贷风险管理中的可行性

精算学是根据经济学的基本理论，运用数学与统计学方法，结合经济，金融，保险等理论，对各种经济活动中的财务风险进行分析，估值和管理的综合性应用科学。我们在对于银行的信贷风险度量中主要使用了死亡率模型和复合泊松分布。

（一）死亡率模型的可行性

寿险精算中存在死亡和生存两种状态，相对应的，信用风险发生结果也可分为违约和不违约两种情况。这些背景下，人的死亡与借款人的违约现象是相似的，换句话说，人的死亡率解析分布与信贷违约概率分布是相似的。因此，利用寿险精算中死亡率模型分析方法来定量研究商业银行借款人的违约概率成为了可能，我们可以以此为依据就有可能测算出商业银行贷款的违约损失，揭示商业银行信用风险发生的数量规律。

（二）复合泊松分布的可行性

复合泊松过程是对于齐次的泊松过程的一个改进。泊松过程是一种典型的而又簡单的随机过程，可以用来很好的对事件发生的次数和过程进行描述。而复合泊松过程又加入了时间发生强度的随机变量，使得更加的贴近生活实际，让信贷风险的度量更加的准确。

在实际中，我们必须为损失时间的发生选择一个模型，因为银行管理部门难以掌握大量的相关数据来确定损失时间的分布。为了描述“稀有事件”，最好的选择是只含一个参数λ的泊松分布。如果用泊松分布描述违约次数，则称贷款组合的违约损失总量S服从复合泊松分布。

使用复合泊松分布对于建立银行贷款风险计量模型具有两方面的意义。一、研究的整个银行贷款违约损失总量需要考虑多个等级的贷款组合，一般来说，这些组合之间又是相互独立的，每一个组合的违约损失都可以用复合泊松分布描述，所要研究的整个银行贷款违约损失总量就可以用复合泊松分布来描述。二、研究跨年度的违约损失总量需要考虑同一等级的贷款在若干个年度中违约损失总量的分布情况，一般来说，这些个别年度的违约损失总量是相互独立的，尽量它们可能具有不相同的分布，违约损失的总量也就会服从复合泊松分布。

四、建议

对银行信贷管理存在的问题提出以下建议：

（1）强化贷款决策的程序，建全贷款的评估决策机制。贷款时要对企业资产和负债状况、经营状况以及偿债能力等方面进行综合评估，严格控制企业借款额度。这样使得银行贷款出现的违约率下降。

（2）转变风险防范观念，建立以风险控制为目标，防范风险与控制风险相结合的信贷风险管理制度。根据对贷款的安全进行定期评估，力争使每一笔贷款都能在银行的监督下。及早发现违约风险和采取损失控制措施，控制银行信贷风险。使得银行可以及早的发现损失并控制，降低出现违约时的损失。

（3）在进行贷款时，根据企业不同的经营环境，确定不同企业的贷款年限，这样可以尽可能的控制由于贷款时间过长所出现的不确定性。同时需要考虑宏观经济环境，以应对利率，汇率等出现变动的突发情况。