非理想1/4波片对泵浦光偏振态的影响

2017-04-10陈运达汪之国江奇渊李莹颖

中国光学 2017年2期

关键词：入射光偏振光偏振

陈运达，汪之国，江奇渊，李莹颖，黄云

(国防科学技术大学光电科学与工程学院，湖南长沙 410073)

非理想1/4波片对泵浦光偏振态的影响

陈运达，汪之国*，江奇渊，李莹颖，黄云

(国防科学技术大学光电科学与工程学院，湖南长沙 410073)

为了研究调整架角度误差以及波片与光源波长不匹配对线偏振光经过1/4波片之后偏振态的影响，本文利用坐标变换法得到1/4波片的琼斯矩阵，并用琼斯矩阵表示各偏振态。推导出波片与光源不匹配时对偏振态的影响理论模型。当考虑到调整架的角度误差时，对入射光偏振态以及波片的琼斯矩阵表达式做引入角度误差的泰勒展开，最后得到和实验结果匹配的仿真曲线。仿真结果表明，当采用808 nm 1/4波片对795 nm波长的线偏振光作用时，在不考虑调整误差的理想情况下出射光椭圆度最高为0.974 6，考虑调整误差时，对应理想情况下椭圆度最高为0.96，椭圆度最高点偏移1.72°。仿真和实验结果为进一步分析泵浦光椭圆度对原子参数的影响提供了依据。

偏振光；1/4波片；琼斯矩阵；泰勒展开

1 引言

原子自旋陀螺(ASG)是一种重要的用于高性能惯性导航的原子自旋传感器，它被认为是未来高精度小尺寸陀螺仪的主要发展方向。ASG是利用原子自旋性质实现的一种陀螺仪[1-4]，从19世纪60年代开始，就已经有研究者致力于开发利用原子核自旋角动量进行转动测量。但是由于这种陀螺对磁场和电场都极为敏感，其精度只能停留在导航层级。随着微纳加工工艺的日臻完善，这种陀螺仪又重新得到人们关注。由于原子自旋陀螺仪结构简单，小尺寸下依然能保持较高精度[5-6]，因此利用微纳加工工艺实现的芯片级原子自旋陀螺仪精度有望达到导航应用要求。到70年代末期，立顿公司就研制出了精度达到导航级别的实验室样机。近年来Northrop-Grumman研制的核磁共振原子自旋(NMRG)陀螺仪标志着微小型，高精度陀螺仪取得革命性的成果(体积只有10 cm3,漂移稳定性优于0.01 deg/h)。国内关于原子陀螺仪的研究工作起步不久，主要有北京自动化设备研究所、北京航空航天大学等院所，研制的NMRG精度优于1 deg/h。

在NMRG的研究工作中，对原子进行光泵浦使原子数在基态上产生非热平衡分布是关键的一环，这个过程称之为极化[7]。理论上来讲，泵浦光应该是圆偏振光，每一个光子携带一个单位的角动量，使得原子每吸收一个光子，最终增加1/2个单位的角动量。但是实验发现实际的铷原子蒸气极化率远低于利用激光器输出功率以及铷弛豫参数得到的计算值，这与光学器件的非理想问题密不可分。例如无论怎么旋转波片，泵浦光都带有一定的椭圆度而非理想的圆偏振光[8],当泵浦光为椭圆偏振光时，平均每个光子携带的角动量要低于理想圆偏振光的光子所携带的角动量，并且光子角动量传递给碱金属原子核外价电子时的效率也会降低，因而影响到碱金属蒸气的极化率，进而对信号强度、信噪比、弛豫时间等参数产生影响。由于原子对左、右旋圆偏振光的吸收截面不同，当泵浦光为椭圆偏振光时，需要将其看作左旋圆偏振光和右旋圆偏振光的合矢量。

2 光泵浦作用的理论分析

2.1 核磁共振陀螺仪工作原理

原子自旋陀螺仪的工作原理是基于原子的自旋。自旋是物质的内禀属性，原子的自旋由电子自旋与核自旋组成。原子自旋角动量在惯性空间中具有定轴性，其与转子陀螺仪中的高速转子在惯性空间中的定轴性类似。因此，利用原子自旋可以进行角运动的测量。有磁场存在的时候，由于核自旋磁矩(自旋磁矩与自旋角动量通过旋磁比可以相互换算)，核自旋会围绕磁场进行拉莫尔进动，该进动频率与载体相对惯性空间是否转动无关。只有采用光泵浦之后，才会有非零的宏观磁矩。当载体相对惯性空间转动时，检测激光测量到的核自旋进动频率是拉莫尔进动频率与载体转动角速率的叠加。因此可以在检测激光测量得到的进动频率中扣除拉莫尔进动频率从而获得载体的转动速率[9]。

图1 核磁共振陀螺工作原理示意图Fig.1 Schematic diagram of basic working principle of NMRG

2.2 碱金属原子的能级分裂

图2 87Rb原子的能级分裂图Fig.2 Energy level splitting of87Rb

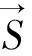
2.3 光泵浦作用的原理

图3 泵浦光对Rb原子作用示意图Fig.3 Schematic diagram of effect of pumping light on Rb atoms

3 1/4波片的琼斯矩阵

3.1 波片琼斯矩阵的推导

设波片快轴方向与x轴成角度θ，如图4所示。

由于振动方向沿慢轴方向的光的光速较小，折射率及光程较大，故相比于沿着快轴方向振动的光有相位延迟量δ，将入射光矢量X1、Y1投影到快、慢轴：

图4 波片主轴与直角坐标系位置关系Fig.4 Position relation between principal axis of wave plate and rectangular coordinates

考虑到相位差之后再重新沿着几何坐标系x、y方向分解，可以得到出射光的表达式[12]：

理想情况下，对波长1/4波片产生的相位延迟量为π/2，得到快轴与x轴成角度θ时出射光的一般表达形式：

波片的琼斯矩阵表示为：

3.2 808 nm波片对795 nm入射线偏振光的作用

由于厂家批量生产的零级波片不可能涵盖每一个波长，所以实验中经常遇到波片和入射光波长不匹配的情况，此时波片对入射光的作用不符合理论值。因此分析波片与入射光波长不匹配时对出射光偏振态的影响十分有必要。

先不考虑调整架误差，分析出射光的偏振态。当波长不匹配时，光经过波片之后是一束斜椭圆偏振光，o光和e光的相位差记为δ=π/2，设波片快轴与x轴夹角设为0，并设入射线偏振光偏振面x轴，当选用808 nm的波片时，出射光相位差δ=0.508 2π rad，当波片快轴与x轴夹角为45°时，波片的琼斯矩阵表示为：

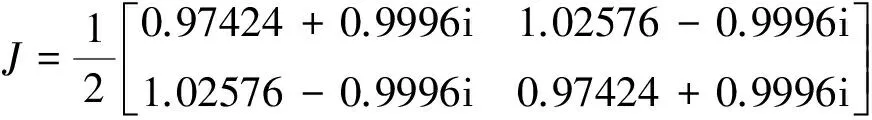
入射光为线偏振光，用琼斯矩阵表示为：

出射光的琼斯矢量为：

sin(2

当椭圆度ε较小时，χ≪1，近似有：

χ=tanχ=sin(2

椭圆度可以表示为：

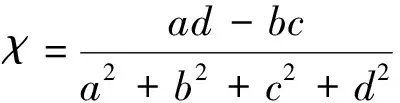
在入射光偏振面离波片快慢轴夹角偏离45°夹角较大时，应由式(10)求椭圆度。

定义入射光偏振面与x轴夹角的变化区间为[0,π/2],结合式(7)到式(10)建立数学模型得到仿真曲线(见图5)。

图5 不考虑调整架误差，795 nm线偏振光经过808 nm 1/4波片后的椭圆度绝对值随入射角度的变化曲线Fig.5 Variation curve of the absolute value of the ovality of emergent light passing through 808 nm 1/4 wave plate with the angle of incident light polarization plane when angle error of the adjustment frame is not considered

当入射光线偏振面与x轴夹角为0或π/2，此时线偏振光与快轴的夹角都为45°，此时出射光最接近圆偏振光，椭圆度为0.974 6，之所以椭圆度的绝对值不为1，是因为采用的波片与入射光中心波长不匹配，当入射光线偏振面与x轴成45°夹角，此时入射光线偏振面与快轴重合，出射光近似为线偏振光，椭圆度近似为0。

理想的情况下，当入射光偏振面与快轴成45°夹角时，能得到最理想的圆偏振光，但是由于实际条件所限，不可能达到完全理想[14]，实验室调整架一般可以控制在0.1°=0.001 75 rad的偏差，考虑到偏差量，当快轴与x轴夹角接近45°时，通过旋转1/2波片改变线偏振光入射角度并在理想值附近将入射光表达式做泰勒展开，由泰勒公式，当f(x)在(x0-δ,x0+δ)有n阶连续导数，则对任意|h|<δ,有：

f(x0+h)=f(x0)+hf′(x0)+…+

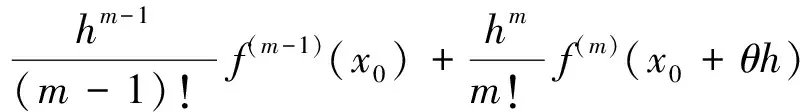
取到一阶近似，得到入射线偏振光x、y分量分别为：

sin(α+0.1)=sinα+0.00175cosα.

得到入射光的琼斯矩阵表达式为：

再考虑到主光轴与x轴的夹角与理想值相比也有误差[15-16]，在确定主轴方位(以快轴与x轴夹角45°为例分析)时，误差在1°=0.017 5 rad范围内，对波片琼斯矩阵的各矩阵元也做一阶近似的泰勒展开，由：

cos(θ+h)=cos(π/4+0.0175)=0.6947

sin(θ+h)=sin(π/4+0.0175)=0.7195 .

此时波片的琼斯矩阵表达式为：

得到出射光关于入射光偏振方向与x轴夹角的琼斯矩阵表达式为：

结合式(8)～式(10)建立数学模型得到仿真曲线(见图6)。

图6 考虑调整架误差，795 nm线偏振光经过808 nm 1/4波片后的椭圆度绝对值随入射角度的变化曲线Fig.6 Variation curve of the absolute value of the ovality of emergent light passing through 808 nm 1/4 wave plate with the angle of incident light polarization plane when angle error of the adjustment frame is considered

当考虑到调整角度误差时，对应理想情况下椭圆度最高位置处的椭圆度为0.96，椭圆度最高点偏移1.72°。

3.3 实验时 808 nm波片对795 nm入射线偏振光的作用

泵浦光路所用到的光学元件中，对偏振态影响最大的为1/4波片，设计光路以分析808 nm波片对795 nm入射线偏振光的作用。

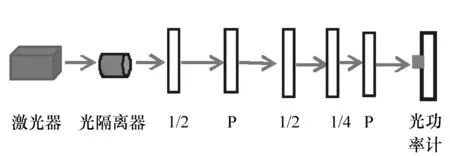
图7 实验光路图Fig.7 Experimental optical path

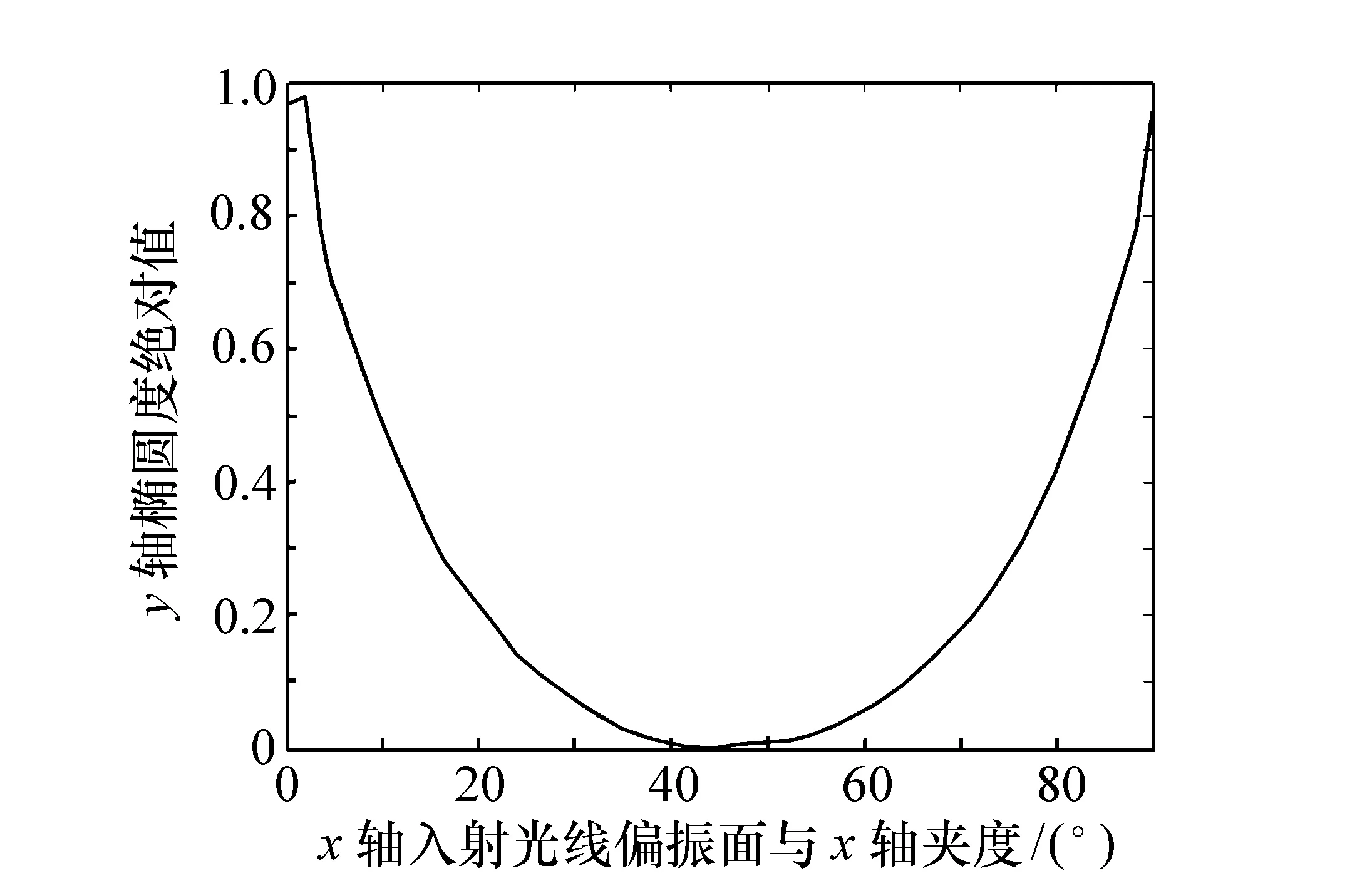
图8 实测数据曲线Fig.8 Measured data curve

实验方案：将1/4波片的快轴调整为和x轴成45°角，将第一个线偏振片作为起偏器，透偏方向调整为水平方向，激光器出射光经过光隔离器后，由1/2波片改变线偏振面至和x轴重合，再通过第二个1/2波片改变偏振角，光线在所有元件表面都近似垂直。使入射线偏振光的偏振面与快轴的夹角在(0,45°)范围内变化，第二个线偏振片作为检偏器，旋转一周[17-18]，光功率计得到一个最小值，一个最大值，两者之比即为出射光椭圆度的平方，得到实测曲线(见图8)。

根据实测曲线，椭圆度最高点位置相对于理论值也有偏差，偏差量在2°左右，与考虑误差时的仿真曲线相符。

但是实测曲线的曲率相对于仿真曲线要小，这是因为由于调整架的精度所限，不可能选取跟仿真时一样多的样本点。

除了角度误差以外，入射光在波片前表面的入射角度也会影响到偏振态，相比于正入射的状态，入射角不为0的时候，光波经过波片的光程差会增大。

椭圆度最大位置为0.98，与仿真结果略有差异，这是因为虽然采用的光源近似为单色光，但仍有一定的线宽。

其他的光学元件，如光隔离器与1/2波片，虽然理论上来讲对偏振态没有影响，但是实际上也会影响到偏振态，比如1/2波片，由于在波片生产过程中切割的误差，使得出射光的o光和e光分量的相位差不是严格的π，所以影响偏振状态。

4 结论

通过对入射光沿垂直方向分解，并用坐标变换的方法得到1/4波片的的琼斯矩阵表达式。结合在实验过程中遇到的问题，提出并分析了当零级波片与入射光波长不匹配时对出射光偏振态的影响。

当不考虑调整角度误差时，理论上795 nm的线偏振光经过808 nm波片之后椭圆度最好可以达到0.974 6，说明波长不匹配时，出射光不可能是理想的圆偏振光，不匹配的影响不可以忽略。

由于实际用到的调整架精度有限，因此引入了误差分析，对入射光的琼斯矩阵表达式以及波片的琼斯矩阵表达式在误差范围内做泰勒展开，得到新的琼斯矩阵表达式，仿真结果显示，椭圆度最高点对应的角度偏移1.72°。最大值与不考虑角度误差时接近。

最后设计光路，得到实测数据曲线，椭圆度最高点对应的角度偏移量约为2°，与仿真结果相符。并对实际数据曲线与仿真曲线的不同之处做出了合理的分析。

本文的研究结果为进一步研究泵浦光对碱金属原子的作用提供了基础，对优化参数分析模型具有重要意义。

[1] 严吉中，李攀，刘元正.原子陀螺基本概念及发展趋势分析[J].压电与声光,2015,37(5)：810-817. YAN J ZH,LI P,LIU Y ZH. Analysis on the basic concept and the development tendency of atomic gyroscopes[J].Piezoelectric&Acoustoopics,2015,37(5):810-817.(in Chinese)

[2] 刘院省,王巍,王学锋.微型核磁共振陀螺仪的关键技术及发展趋势[J].导航与控制,2014,13(4):1-6. LIU Y X, WANG W, WANG X F. Key technology and development tendency of micro nuclear magnetic resonance gyroscope[J].NavigationandControl,2014,13(4):1-6.(in Chinese)

[3] 周鹏, 李夜兰.国外核磁共振陀螺技术专利研究[J].战术导弹技术,2015,(4):5-9. ZHOU P, LI Y L. Patent information research on the nuclear magnetic resonance gyroscope technology[J].TacticalMissileTechnology,2015(4):5-9.(in Chinese)

[4] 秦杰，汪世林，高溥泽,等.核磁共振陀螺技术研究进展[J].导航定位与授时，2014,2(1):64-69. QIN J,WANG S L,GAO B Z,etal.. Advances in nuclear magnetic resonance gyroscope[J].NavigationPositioning&Timing,2014,2(1):64-69.(in Chinese)

[5] LUTWAK R. Micro-technology for positioning, navigation, and timing towards PNT everywhere and always[C]. 2014 International Symposium on Inertial Sensors and Systems(ISISS),IEEE,2014: 1- 4.

[6] MEYER D,LARSEN M. Nuclear magnetic resonance gyro for inertial navigation[J].GyroscopyandNavigation,2014,5(2):75-82.

[7] HAPPER W,JAU Y Y,WALKER T.OpticallyPumpedAtoms[M]. Weinheim:Wiley-VCH Verlag GmbH & Co,2010:159-217.

[8] 任树锋，王秀霞.线偏振光通过多个任意厚度波片的偏振态[J].激光技术，2014,38(3):394-397. REN SH F,WANG X X. Polarization States of linearly polarized light transmitting through several wave-plates with arbitrary thickness[J].LaserTechnology,2014,38(3):394-397.(in Chinese)

[9] DONLEY E. A. Nuclear magnetic resonance gyroscopes[C]. 2010 Conference on Sensors,IEEE,2010:17-22.

[10] HAPPER W. Optical pumping[J].ReviewsofModernPhysics,1972,44:169-249.

[11] KASTLER A. Optical methods of atomic orientation and of magnetic resonance[J].JOSA,1957,47(6):460-465.

[12] 蔡履中.光学[M].北京:科学出版社，2007. CAI L ZH.Optics[M]. Beijing:The Science Publishing Company,2007.(in Chinese)

[13] 汪之国，龙兴武，王飞,等.激光陀螺本征模偏振态与磁敏感特性的理论研究[J].物理学报，2013,62(5)：054205. WANG ZH G,LONG X W,WANG F,etal.. Theoretical analysis of polarization eigenstate and magnetic sensitivity in a ring laser gyro[J].ActaPhys.Sin.,2013,62(5)：054205.(in Chinese)

[14] 王薇，谢宇，许露露.偏振光经过1/4波片之后偏振态的变化[J].淮北煤炭师范学院院报，2010,32(2):26-29. WANG W,XIE Y,XU L L. Research on change of the polarization status for the polarized light passing through quarter wave plate[J].J.HuaibeiCoalIndustryTeachersCollege,2010,32(2):26-29.(in Chinese)

[15] 赵廷生，李国华.精确确定光路中1/4波片光轴方位的新方法[J].光学学报，2008,28(3):487-491. ZHAO T SH,LI G H. A new method to measure the optical-axis azimuth of quarter-wave plate in light path accurately[J].ActaOpticaSinica,2008,28(3):487-491.(in Chinese)

[16] 任广军，李国华.偏光器件的Jones矩阵研究[J].光学技术,2003,29(5):578-580. REN G J,LI G H. Jones matrix research of polarization device[J].OpticalTechnique,2003,29(5):578-580.(in Chinese)

[17] 白云峰，闫照宇，浦合力.仅使用偏振片精确测量偏振态[J].黑龙江工程学院学报，2014,28(1):64-66. BAI Y F,YAN Z Y,PU H L. Polarization measurement with polarizer only[J].J.HeilongjiangInstituteofTechnology,2014,28(1): 64-66.(in Chinese)

[18] 赵航，郝彦军,朱俊,等.光的偏振特性研究[J].实验科学与技术，2015,6(13):1-2. ZHAO H,HAO Y J,ZHU J,etal.. Research on feature of polarized light[J].ExperimentScienceandTechnology,2015,6(13):1-2(in Chinese).

《光学精密工程》(月刊)

● 中国光学开拓者之一王大珩院士亲自创办的新中国历史最悠久的光学期刊

● 现任主编为国家级有突出贡献的青年科学家曹健林博士

● Benjamin J Eggleton, John Love等国际著名光学专家为本刊国际编委

《光学精密工程》主要栏目有现代应用光学(空间光学、纤维光学、信息光学、薄膜光学、光电技术及器件、光学工艺及设备、光电跟踪与测量、激光技术及设备)；微纳技术与精密机械(纳米光学、精密机械)；信息科学(图像处理、计算机应用与软件工程)等。

❋ 美国工程索引EI核心期刊

❋ 中国出版政府奖期刊提名奖

❋ 中国精品科技期刊

❋ 中文核心期刊

❋ 百种中国杰出学术期刊

❋ 中国最具国际影响力学术期刊

主管单位：中国科学院

主办单位：中国科学院长春光学精密机械与物理研究所

中国仪器仪表学会

地址：长春市东南湖大路3888号邮编：130033

电话：0431-86176855 传真：0431-84613409

电邮：gxjmgc@sina.com 网址：http://www.eope.net

定价：100.00元/册

Influence of nonideal 1/4 wave plate on pump light polarization

CHEN Yun-da, WANG Zhi-guo*, JIANG Qi-yuan, LI Ying-ying, HUANG Yun

(CollegeofOptoelectronicScienceandEngineering,NationalUniversityofDefenseTechnology,Changsha410073,China)

*Correspondingauthor,E-mail:maxborn@nudt.edu.cn

In order to study the influence of the angle error of adjusting frame and mismatching of the wavelength of the light source with the wave plate on linearly polarized light after passing through 1/4 plate, the Jones matrices of 1/4 wave plate is obtained in this paper by using coordinate transformation method, and the representation of each polarization state is derived from the Jones matrix. Then the theoretical model of the influence on the polarization are deduced when wave plate and light source do not match with each other. When the angle error of the adjusting frame is considered, the Taylor expansion about the Jones matrices of the polarization state of incident light and wave plate are derived as the angle error and get the simulation curve matching with experimental result. Simulation results indicate that in the case of not considering the adjustment error, the ovality of the emergent laser is 0.974 6 when using the 808 nm 1/4 wave plate on linearly polarized light with the 795 nm wavelength; and in the case of considering the adjustment error， the ovality is 0.96 corresponding to the highest point under ideal condition as well as the highest point of the ovality offsets 1.72°. The simulation and experimental results provide the basis for further analysis of the influence of the pump light with different ovality on atomic parameters.

polarized light;1/4 wave plate;Jones matrix;Taylor expansion

2016-08-30；

2016-09-28

国防科技大学预研项目(No.JC140702) Supported by Research Project of National University of Defense Technology(No.JC140702)

2095-1531(2017)02-0226-08

O431.2； O436.3

10.3788/CO.20171002.0226