轮轨振动行为下高速轮轨滚动接触瞬态特性分析

肖　乾，昌　超，王立乾，王　磊,4

(1.华东交通大学 载运工具与装备教育部重点实验室，江西 南昌　330013；2.西南交通大学 牵引动力国家重点实验室，四川 成都　610031；3.中国铁道科学研究院 铁道科学技术研究发展中心，北京　100081；4.中车青岛四方股份责任有限公司，山东 青岛　266111)

当前，国内外学者研究轮轨滚动接触特性时基本上是将其近似处理为静态和稳态问题，认为轮轨接触参数均保持常量。魏云鹏[1]通过建立完整的轮轨系统有限元模型，分析蛇形运动状态下轮轨滚动接触参数对接触斑面积、形状、Mise应力等接触特性的影响，得出横移量的影响程度要大于摇头角的结论。肖乾[2-3]采用mixed Lagrangian-Eulerian方法分析了横移、冲角等接触参数对于轮轨蠕滑特性的影响。王彩芸[4]采用基于非Hertz滚动接触理论和数值计算方法，分析了静态接触下滚动接触参数中横移量、摇头角的变化对轮轨接触之间蠕滑力、接触斑黏滑区的分布以及等效应力等接触特性的影响。Knothe和Gross-thebing[5-6]将动态轮轨滚动接触参数和蠕滑率代入稳态滚动接触理论中，得出了轮轨滚动接触参数与轮轨黏着之间的变化关系。常崇义[7]基于ALE有限元法对不同横移量下轮轨接触斑内的摩擦力、速度矢量分布等接触特性进行研究，结果表明接触斑内存在明显的自旋效应且随着横移量的不同存在差异。以上研究大多建立的是三维静态或稳态弹塑性轮轨滚动接触模型，难以真实有效地仿真计算轮轨的接触特性。实际上在轮轨滚动接触过程中，轮轨呈现振动状态，故其接触参数也是不断变化的[8]，而轮轨接触参数的变化会对轮轨的接触特性产生影响。

本文通过建立轮轨振动行为下的三维高速轮轨滚动接触瞬态模型，研究高速列车在直线线路上运行时的瞬态接触特性，为准确分析高速列车轮轨磨耗和滚动接触疲劳提供基础数据。

1　高速轮轨振动分析

1.1　轮轨滚动振动接触简化模型

高速列车车辆模型中，转向架中央悬挂模型包括钢弹簧(提供3个方向的刚度和阻尼)、橡胶块(提供横向止档)及抗蛇行减振器、横向减振器和垂向减振器(提供阻尼)；轴箱悬挂模型包括轴箱弹簧(提供3个方向的刚度)、轴箱定位装置(提供水平刚度)和悬挂在轴箱弹簧外侧的一系垂向减振器(提供一系垂向阻尼)。对高速列车车辆模型进行分析可知，在轮轨振动行为下轮轨滚动接触是弹性的，可以将其视为刚度值一定的1个弹簧系统，该弹簧系统将车轮和钢轨的质量关联在一起，并且与轮对上部的悬挂系统形成1个阻尼振动系统。因车辆悬挂系统的刚度远远大于轮轨接触刚度，故可以视车体和转向架施加给轮对的作用力基本不变。轮轨间的垂向远小于其切向力，因此只考虑垂向力的作用[8]。

轮轨振动行为下轮对与钢轨的接触可以简化为图1所示的轮轨滚动振动接触简化模型。图中：J1，J2和J3分别为车体、轮对和钢轨点头的转动惯量；m1，m2和m3分别为车体、构架以及轮对的质量；K1和C1分别为车体与构架之间的垂向刚度和阻尼；K2和C2分别为构架与轮对之间的刚度和阻尼；v为车辆前进速度。

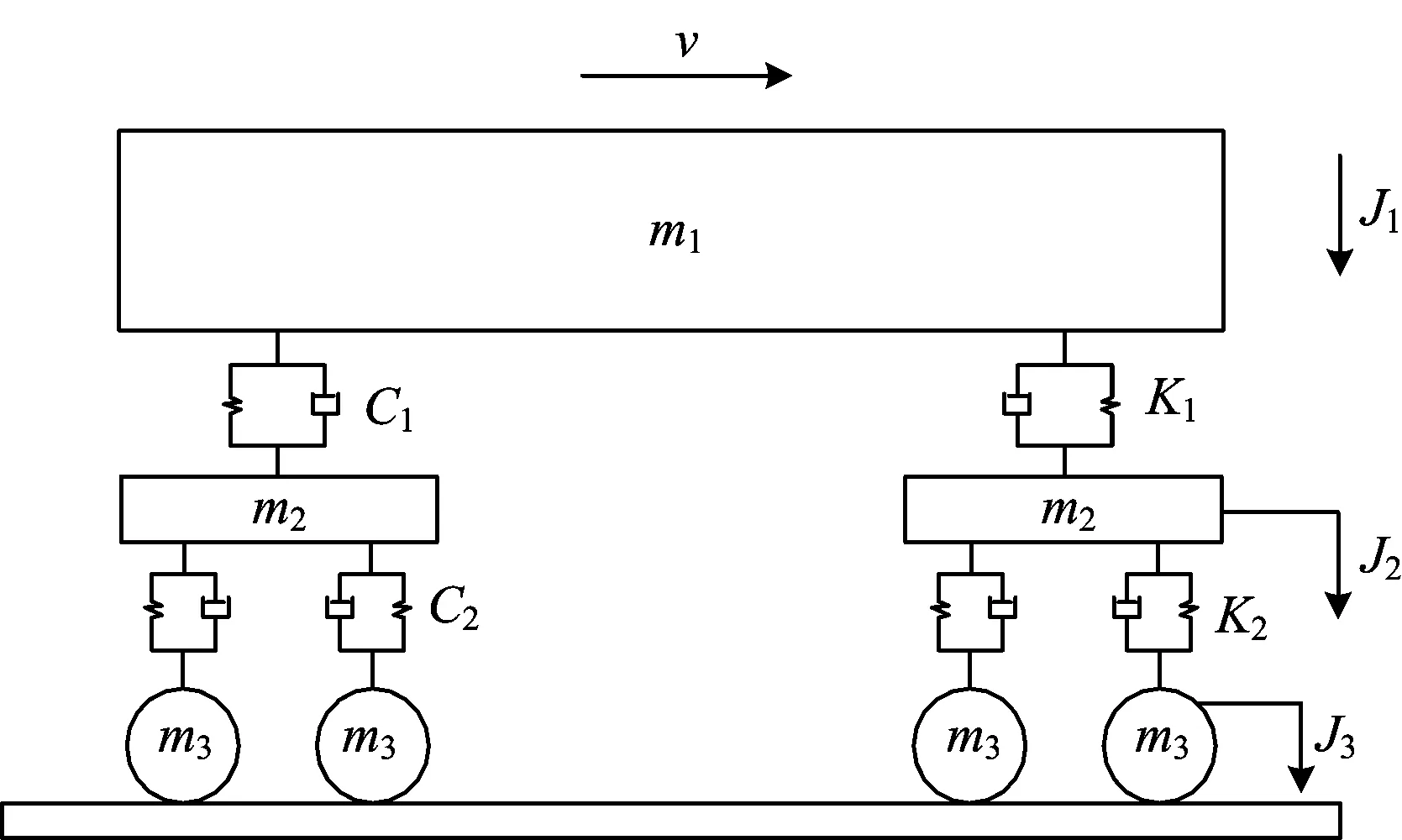
图1　轮轨滚动振动接触简化模型

因为轮轨滚动接触基本符合Hertz弹性接触理论的所有假设条件[9]，所以可将轮轨接触处近似看作1对椭球体，并应用该理论作为建立动力学模型的基础。假设轮轨的接触变形为zH，则由该理论可以得到轮轨间的轮轨力F为

(1)

其中，

对于轮对跳起而脱离轨面(即zH<0)的现象，称之为轮轨接触脱离。

在轮轨滚动接触过程中，考虑到轮轨接触脱离情况的振动接触系统运动方程为

FP-C(δH)3/2H(zH)

(2)

式中：m为轮对的质量；C为悬挂系统阻尼；FP为轮对所受作用力；t为时间。

1.2　数值模型及计算结果

以CRH2型高速列车为研究对象，基于图1所示的轮轨滚动振动接触简化模型和车辆多体动力学理论，运用多体动力学软件UM建立头车模型，该头车模型将头车简化为车体、构架、轮对3类质量体以及连接它们的系统悬挂部件，同时将轮轨接触几何关系的非线性、横向止档的非线性、抗蛇行减振器的非线性以及一系悬挂的非线性等均考虑到模型内，而且将高速列车头车动力学仿真模型设置为刚体结构[11]，模型参数见表1，数值模型如图2所示。

图2　高速列车多体动力学数值模型

表1　CRH2型高速列车基本参数

对于图2所建立的高速列车多体动力学模型，设置其运行速度为300 km·h-1，在直线轨道上运行12 s。由于轮对的对中性，本文以左轮为例，得到的轮轨垂向力、轮对横移量和轮轨冲角的时程曲线如图3—图5所示。

图3　轮轨垂向力随时间变化曲线

图4　轮对冲角随时间变化曲线

图5　轮对横移量随时间变化曲线

由图3可以看出：轮轨的垂向振动尤为明显；轮轨垂向力随时间的变化曲线可以近似为呈周期性变化，周期约为0.1 s，振动频率大约为10 Hz；最大垂向力为115 751.8 N，最小为688.4 N，分别是轮轨静载荷的1.938倍和0.012倍，最大轮轨垂向力小于我国《高速试验列车动力车强度及动力学性能规范》(95J01-L)中给出的每个车轮作用于轨道的垂向力峰值极限值170 kN，在安全允许范围内；最小的垂直力则反映车轮的轮重减载率，车辆在运行过程中，车轮会因为振动和轮对横向力作用而发生减载，大量动力学试验表明，车辆可能单侧轮重减载过大，此时即使极小的轮对冲角也容易产生较大的横向力，引发脱轨。此处计算得的轮重减载率为0.011 5。

由图4和图5可以看出：轮对冲角的振动周期约为0.05 s，振动频率约为20 Hz，振幅为1.568 mrad；轮对横移的振动周期约为0.95 s，振动频率约为1.05 Hz，振幅为5.26 mm。

图3—图5所示的数值仿真结果与文献[12—14]中相关的实测结果有较好的一致性，可作为轮轨振动行为下轮轨滚动接触瞬态分析的输入参数。

2　三维高速轮轨滚动接触瞬态有限元模型

以CRH2型高速列车的车轮几何尺寸和材料弹塑性本构特征，选用mixed Lagrangian-Eulerian方法建立高速列车轮轨滚动接触瞬态模型。模型构建时要求同时给出车轮的前进速度v和转动角速度ω。钢轨选用国产60 kg·m-1钢轨，钢轨上网格细化加密区最小单元为2 mm，加密区长度为100 mm；车轮网格细化区为车轮的1/6，最小单元也是2 mm。接触面定义为有限滑移的面—面接触，车轮接触面设置为主面，钢轨的接触面设置为从面；应用罚函数法定义切向接触特性为干摩擦，根据试验结果，不同载荷和速度下轮轨间的摩擦因数基本处于0.18～0.20之间[15]，本文摩擦系数取0.2，法向接触定义为硬接触。由于模型设定的钢轨长度较短，对钢轨两端自由度会造成影响，所以需要对钢轨端面和底面进行全约束；将车轴设定为刚体，轴重为14 t，施加至车轴两端处；设车轮和钢轨的弹性模量和泊松比保持一致，分别为205 GPa和0.3；轨底坡设为1/40，车轮、钢轨和车轴的密度为7 800 kg·m-3，轮对和钢轨的塑性应变与真实应力的关系如图6所示。

图6　塑性应变与真实应力的关系曲线

对高速列车轮轨滚动接触瞬态模型先采用ABAQUS/Standard隐式求解器求解稳态结果，并将计算结果在ABAQUS/Explicit显式求解器中重新启动，建立三维高速轮轨滚动接触瞬态有限元模型如图7所示。

图7　三维高速轮轨滚动接触瞬态有限元模型

3　轮轨振动下的滚动接触瞬态特性分析

本文设置在速度v=300 km·h-1情况下的轮轨瞬态接触为研究对象，分析列车在直线轨道上运行时轮轨瞬态接触特性。由图3可知，在周期为0.1s的时间内轮对垂向力呈现周期性波动，为了研究轮轨振动下的轮轨瞬态特性，取振动周期的整数倍作为分析对象，同时去除前0.1 s内的数值振荡时间。综上可取0.2，0.3，0.4，0.5和0.6 s这5个时刻的接触参数对轮轨的接触特性进行分析。

在瞬态有限元模型中设置轮轨处于蠕滑牵引状态，且以由第1部分分析所得不同时刻的接触参数为初始条件，向前滚动1.5 ms后，车轮瞬态滚动过程很快趋于稳定。在该时间间隔内，左轮(由于左、右车轮的对称性，下文只给出左轮在各时刻的接触特性统计结果。)纵、横向蠕滑力和接触斑面积如图8—图10所示。

图8　不同时刻时横向蠕滑力的变化曲线

图9　不同时刻时纵向蠕滑力的变化曲线

由图8—图10可以看出：在瞬态模型中，车轮刚开始滚动时，有1个较大的左右晃动过程，表现为横向蠕滑力在起始的范围内出现较大波动，之后开始过渡到稳定状态，稳定后横向蠕滑力的均值为1 239.07 N；在蠕滑牵引状态下，纵向蠕滑力在刚刚滚动时刻出现了蠕滑制动的情况，随着轮对的滚动过程趋于稳定，纵向蠕滑力慢慢在蠕滑牵引状态下呈现周期性波动，在整个瞬态接触过程中，纵向蠕滑力的均值为13 542.11 N。纵、横向蠕滑力在0.2 s的时间间隔内波动较大，纵、横向蠕滑力最大达到27 906.4和16 500.7 N；接触斑面积整体变化走势呈现相似性，其中0.5 s工况下的变化曲线较其他时刻曲线存在小幅度增长，数值偏大。

左侧车轮具体的接触特性参数见表2。由表2中可以看出：在0.2 s这一时刻，纵、横向蠕滑力的平均值比其他时刻大，主要是因为在该时刻的初始条件下轮轨垂向力和轮轨冲角最大，而轮对横移量最小；在0.5 s时刻接触斑面积最大，这是由于该时刻的轮对横移量最大；在一定范围内纵、横向蠕滑力随轮轨垂向力的增大而增大，且纵、横向蠕滑力与接触斑面积呈正相关，这也与图10所示的不同瞬态时间段内接触斑面积的变化相符。

表2　左侧车轮的轮轨接触特性

4　结　论

(1)动力学模型中轮对的轮轨垂向力成周期性变化，周期近似为0.1 s，振动频率大约为10 Hz，轮轨垂向力最大为115 751.8 N，最小为688.4 N，分别为轮轨静载荷的1.938倍和0.012倍，这说明高速列车在运行中的实际情况为振动状态。

(2)轮对横移的振动周期为0.95 s，振动频率为1.05 Hz，振幅为5.26 mm，0.5 s时刻的横移量是0.2 s时刻的7.17倍，且轮轨滚动振动模型稳定以后轮对横移的振动趋势与纵、横向蠕滑力的振动趋势一致。

(3)纵、横向蠕滑力在0.2 s的时间间隔内波动较大，最大分别达到27 906.4和16 500.7 N，分别为0.6 s时刻最大纵、横向蠕滑力的1.3倍和1.1倍，计算结果表明，一定范围内纵、横向蠕滑力与轮对冲角以及接触斑面积呈正相关。

[1]魏云鹏, 吴亚平, 段志东，等. 列车蛇形运动状态下轮轨接触特性分析[J]. 铁道标准设计, 2015,59(3):37-40.

(WEI Yunpeng, WU Yaping, DUAN Zhidong, et al. Analysis of Wheel/Rail Contact Characteristics in Case of Hunting Motion [J]. Railway Standard Design, 2015,59 (3):37-40. in Chinese)

[2]肖乾, 徐红霞, 黄碧坤,等. 轮对横移对高速轮轨稳态滚动接触蠕滑力和蠕滑率的影响[J]. 中国铁道科学, 2014, 35(4):88-93.

(XIAO Qian, XU Hongxia, HUANG Bikun, et al. Effects of the Lateral Displacement of Wheelset on the Creep Force and Creepage of High-Speed Wheel-Rail Steady-State Rolling Contact[J]. China Railway Science, 2014, 35(4):88-93. in Chinese)

[3]肖乾，徐红霞，成棣，等. 不同轮轨冲角下高速轮轨稳态滚动接触的蠕滑特性[J]. 中国铁道科学，2014, 35(1): 60-66.

(XIAO Qian, XU Hongxia, CHENG Di, et al. Creep Characteristics of High-Speed Wheel-Rail Steady-State Rolling Contad under Different Attack Angles [J]. China Railway Science, 2014, 35(1): 60-66. in Chinese)

[4]王彩芸，王文健，郭俊，等. 横移量、摇头角对轮轨滚动接触行为的影响研究[J].机械设计与制造，2012 (12):31-33.

(WANG Caiyun, WANG Wenjian，GUO Jun, et al. Effects of Transverse and Yaw Angle on Rolling Contact of Wheel/Rail [J]. Machinery Design & Manufacture, 2012 (12):31-33. in Chinese)

[5]KNOTHE K, GROSS-Thebing A. Derivation of Frequency Dependent Creep Coefficients Based on an Elastic Half-Space Model[J]. Vehicle System Dynamics, 1986, 15(3): 133-153.

[6]GROSS-Thebing A. Frequency-Dependent Creep Coefficients for Three-Dimensional Rolling Contact Problems[J]. Vehicle System Dynamics, 1989, 18(6): 359-374.

[7]常崇义, 王成国. 基于ALE有限元的轮轨稳态滚动接触分析[J]. 中国铁道科学, 2009, 30(2):87-93.

(CHANG Chongyi, WANG Chengguo. Wheel-Rail Steady State Rolling Contact Analysis Based on ALE Finite Element Method[J]. China Railway Science, 2009, 30(2):87-93. in Chinese)

[8]孙琼. 轮轨接触振动及其对轮轨黏着的影响[J]. 铁道机车车辆, 2002(增1):166-172.

(SUN Qiong. Wheel Rail Contact Vibration and Its Effect on Wheel Rail Adhesion [J]. Railway Locomotive and Rolling Stock, 2002(Supplement 1):166-172. in Chinese)

[9]HERTZ H R. Über Die Berührung Fester Elastischer Körper[J]. Journal Für Die Reine und Angewandte Mathematik,2006,92:156-171.

[10]GREENWOOD J A. Analysis of Elliptical Hertzian Contacts[J]. Tribology International, 1997, 30(3): 235-237.

[11]黄照伟. 车轮磨耗及其对车辆动力学性能的影响[D].成都：西南交通大学， 2012.

(HUANG Zhaowei. Wheel Tread Wear and Its Influence on Dynamic Performance of Vehicles[D]. Chengdu：Southwest Jiaotong University, 2012. in Chinese)

[12]李国顺，金炜，范荣巍. 基于图像识别的轮轨冲角测量系统研究[J]. 中国铁道科学, 2005, 26(5):82-85.

(LI Guoshun, JIN Wei, FAN Rongwei. Research on the Measurement System of the Attack Angle between Wheel and Rail Based on Image Identification [J]. China Railway Science, 2005, 26(5):82-85. in Chinese)

[13]张海洋.激光测距仪测试道岔区轮对横移的应用研究[J].路基工程，2010(1)：153-155.

(ZHANG Haiyang. Study on Application of Laser Distance Measuring Instrument to Testing Wheel Pair Lateral Movement in Turnout Zone [J]. Subgrade Engineering, 2010(1):153-155. in Chinese)

[14]彭波，姚远，向阳，等. 机车车辆半车滚振试验的动力学仿真分析[J]. 电力机车与城轨车辆, 2014，37(2):26-29，32.

(PENG Bo, YAO Yuan, XIANG Yang, et al. Dynamic Simulation of Rolling and Vibration Test for Half Vehicle on Rolling Stock [J]. Electric Locomotives & Mass Transit Vehicles, 2014，37 (2):26-29，32. in Chinese)

[15]刘辉龙, 王新华, 谢小鹏,等. 基于轮轨摩擦试验装置的摩擦因数测量方法[J]. 润滑与密封, 2016, 41(12):107-111.

(LIU Huilong, WANG Xinhua, XIE Xiaopeng, et al. A Measuring Method of Friction Coefficient Based on Wheel-Rail Friction Testing Device [J]. Lubrication Engineering，2016, 41(12):107-111. in Chinese)