泥水盾构开挖面失稳破坏的颗粒流模拟研究

王振飞，张成平

(北京交通大学 城市地下工程教育部重点实验室，北京　100044)

近年来，盾构隧道技术已成为城市地下铁道工程的主流施工方法。开挖面土体的稳定性控制是盾构隧道掘进过程中的关键问题[1-2]。由于开挖面失稳导致地层变位和影响周边建(构)筑物安全的例子不乏出现，如上海大连路隧道曾因为开挖面失稳破坏而引起地面严重塌陷，造成了直接的经济损失[3]。对于泥水式盾构隧道而言，较小的支护压力会诱发隧道开挖面前方围岩不断涌入压力舱，地层沉降显著并引发地表坍塌，而较大的支护压力又易引起地表隆起[4-5]。研究泥水盾构开挖面的稳定性对于确保隧道施工质量和安全的意义重大。

离散元法是当前研究散体介质细观力学行为的常用数值分析手段，该方法通过对颗粒流细观参数的研究来分析材料宏观层次的力学性能[6-8]。关于开挖面稳定性分析的数值计算问题，颗粒流程序PFC2D可有效地模拟土体颗粒间的相互作用、大变形、坍塌和断裂等问题，使其在研究开挖面失稳破坏机理方面具有一定的优势[9-12]。国内外学者主要对盾构隧道开挖面失稳破坏的机理和地表沉降进行研究。在开挖面失稳破坏机理方面，胡欣雨[3,12]等依托钱江隧道和上海长江隧道工程，研究了泥水盾构开挖面从发生失稳破坏至整体破坏的发展过程。时振昊[5]建立了土压盾构动态掘进模型，研究了隧道开挖面支护力与地层损失的关系以及盾构掘进速度对地层损失的影响。缪林昌[10]等采用PFC2D研究了砂土地层盾构隧道开挖面的破坏机理，探讨了盾构隧道掘进时围岩的破坏模式与分布区域。在地表沉降方面，He[13]等以成都地铁1号线为背景，从细观角度分析了砂卵石地层盾构掘进引起的地表沉降规律以及影响压力拱的因素。滕丽和张恒[14]采用PFC2D和Plaxis3D模拟分析了砂卵石地层盾构掘进引起地表沉降的规律，并研究了土压盾构失稳破坏的机理及沉降变形特性。江英超[15]等从细观角度模拟了砂卵石地层中滞后沉降的形成和发展过程，分析隧道埋深和地层空洞位置等因素对滞后沉降的影响。尽管相关学者对盾构隧道开挖面失稳破坏的机理和地表沉降进行了一定研究，但缺少系统全面地研究颗粒流细观参数和泥膜对开挖面稳定性的影响。

本文以北京铁路枢纽北京站至北京西站地下直径线(简称北京地下直径线)盾构隧道为工程背景，通过对比室内试验和基于PFC2D的双轴试验结果，确定砂卵石地层的颗粒流细观参数。从土体的颗粒摩擦系数和接触模量以及泥膜的厚度和强度对开挖面的作用效果进行分析和评价，进而确定保证北京砂卵石地层泥水盾构开挖面稳定的泥水盾构泥膜特性。

1　砂卵石地层颗粒流模型

1.1　颗粒流模型参数标定

可通过基于PFC2D的双轴试验获得土体颗粒集合的应力—应变曲线，并与实际土样的室内试验结果进行对比，进而得到土体的颗粒流模型及参数。对试样的上下左右4个墙体进行加载，其中对上下墙体的加载通过施加速度的方法模拟，而对左右墙体的加载则通过伺服机制约束速度实现，从而保证对墙体施加固定的围压。

土体颗粒在墙体范围内生成，其半径的范围为[Rmin，Rmax]。双轴试验过程中砂卵石地层颗粒分布形态的变化如图1所示。图1(a)为生成小粒径土体颗粒后的模型效果；图1(b)为土体颗粒膨胀(颗粒半径扩大)后的土体颗粒分布形态；图1(c)为土体颗粒膨胀后颗粒达到新的平衡后颗粒分布形态，这种新的平衡是通过增加土体颗粒间摩阻力并采用循环方式实现的；图1(d)为试样加载后土体颗粒的分布形态。

图1　双轴试验中颗粒的分布形态

按照摩尔—库伦准则，土体抗剪强度τ与内摩擦角φ和黏聚力c之间的关系可表示为

τ=c+σtanφ

(1)

式中：σ为偏应力。

偏应力σ可表示为

(2)

式中：σ1为最大主应力；σ3为最小主应力。

依照北京地下直径线的地勘报告，选定砂卵石地层中典型围岩的物理力学参数如下：弹性模量E=90～100 MPa；泊松比μ=0.15；密度ρ=2 150 kg·m-3；黏聚力c=0；内摩擦角φ=40°～45°。

宏观参数与细观参数间的关系可用摩尔—库伦准则建立。在不同最小主应力条件下，采用初始输入参数进行颗粒流试验，通过线性拟合可确定最小主应力σ3与偏应力σ之间的关系，进而确定试样的c和φ。

通过不断试算，最终确定的不同最小主应力条件下偏应力σ随轴向应变ε变化的曲线以及偏应力σ随最小主应力σ3变化的曲线，分别如图2和图3所示。由图2和图3可知，偏应力随最小主应力的增加而增大，轴向应变也随之逐渐增大。

图2　偏应力—轴应变曲线

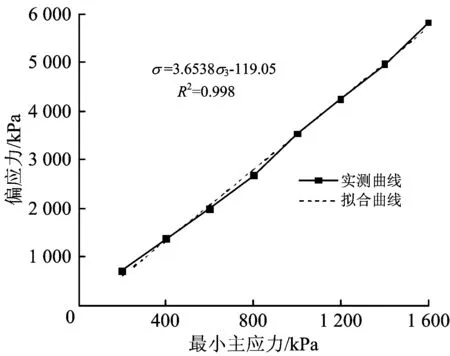
图3　偏应力与最小主应力的关系

不同最小主应力σ3所对应试样模型最终的位移场和剪切破坏带如图4所示。由图4可知，当偏应力达到峰值强度后，3组试样均形成显著的剪切破坏带，这说明试样均已出现破坏。

图4　不同最小主应力下的位移场分布和剪切破坏带

假定弹性模量E50为偏应力峰值强度的一半与轴向应变ε的比值，则典型的现场围岩参数与PFC2D数值试验确定的数值结果见表1。由表1可知，两者的宏观参数是基本相同的，这也说明PFC2D颗粒流模拟所得到的细观参数可代表现场实际的围岩参数。

由PFC2D双轴试验确定的墙体及颗粒流模型参数见表2。

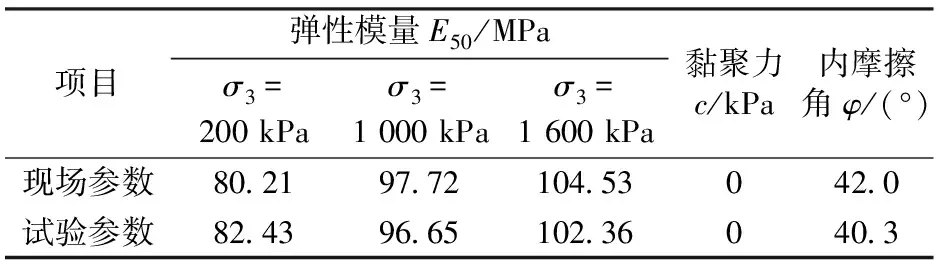
表1　土体宏观参数

表2　墙体及颗粒流模型细观参数

1.2　颗粒流模型

取模型的宽度为57 m、高度为45 m，盾构隧道外径为12 m，埋深为24 m。模型边界共设计8道墙体；其中墙体①，②，⑥，⑦及⑧为模型边界；墙体③，④及⑤为盾构边界。由于含有数量众多的土体颗粒，考虑到计算效率问题，按照缩小的比例尺1/100建立模型，如图5所示。

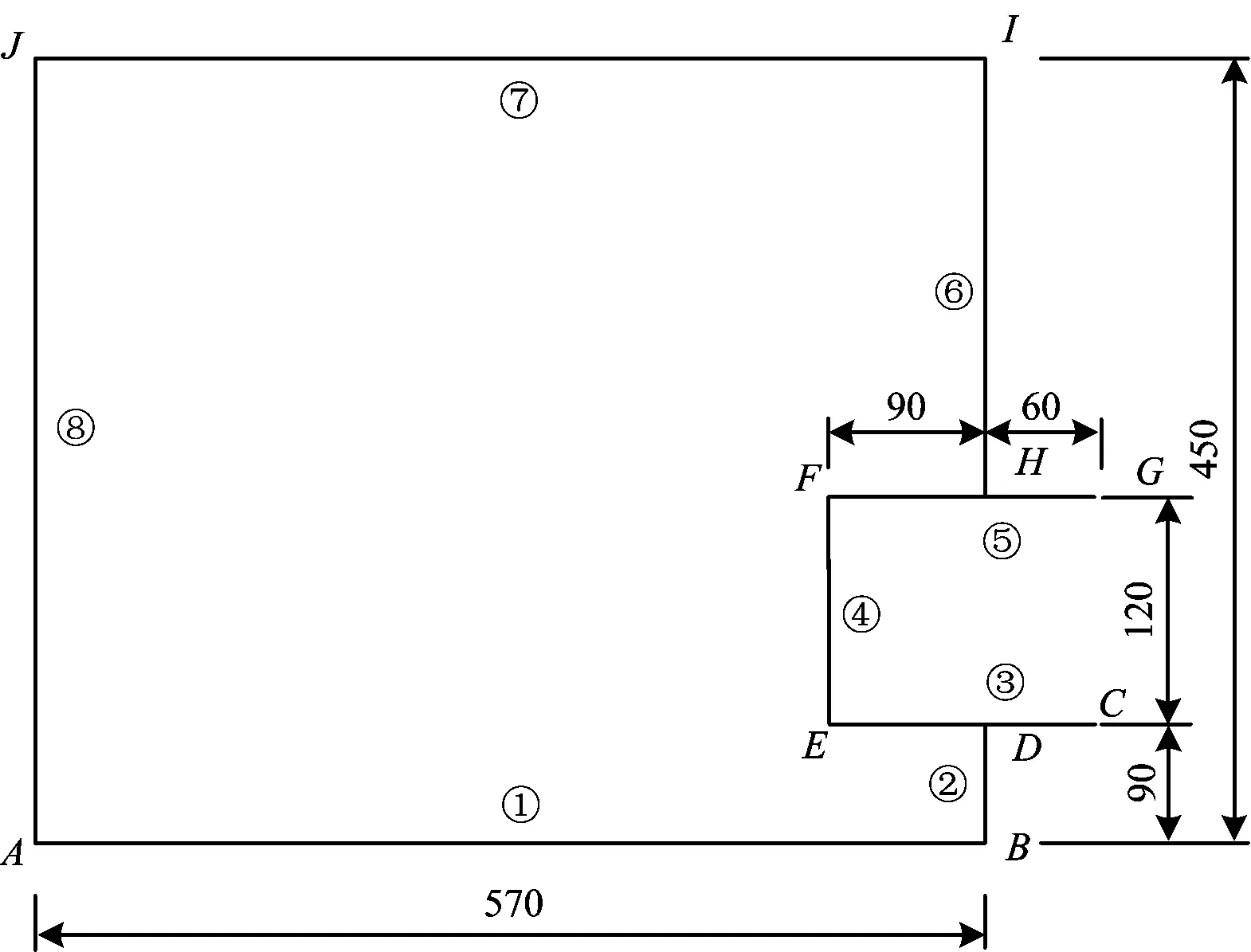
图5　模型平面尺寸(单位:mm)

模型颗粒的生成采用排斥法[16-17]。设置土体颗粒的重力加速度为100g(1g=9.81 m·s-2)，土体颗粒的集合体生成后，在自重应力场下达到平衡。用颜色不同的颗粒将土体划分成如图6所示的网格，网格的数量代表土体参数。划分的网格为正方形，其边长为0.03 m，边长与最大颗粒的半径之比约为12。

经统计计算测量圆的结果表明，垂直压力σv和水平压力σx与地层深度h的线性效果显著，可分别用下式表示为

σv=24.27h

(3)

σx=10.60h

(4)

由式(3)和式(4)可知，地应力环境符合实际情况，也说明了采用PFC2D模拟土体是正确的。

图6　网格划分

1.3　开挖面渐进破坏过程

在自重力场平衡计算完成后，删除墙4以模拟开挖面无支护状态。不同计算阶段的开挖面土体变形情况如图7所示。由图7可知，开挖面土体颗粒首先向洞内滑落；继续运算，滑落土体颗粒的数量不断增加，开挖面围岩应力释放，地层损失增加，开挖面逐渐发生破坏，地层沉降显著并发展至地表，进而引起地面塌陷。

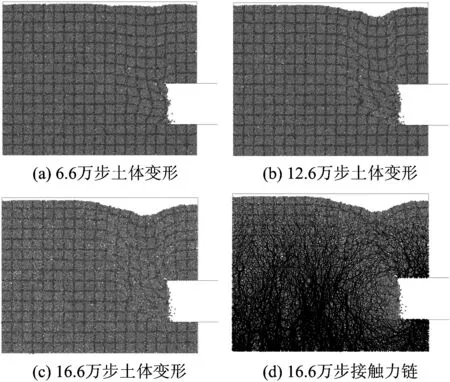
图7　地层渐进破坏过程

由图7(d)可知，开挖面附近土体颗粒间的接触力较小，并未形成粗大、强劲的力链。由于在开挖面前方未出现稳定的压力拱，因此开挖面前方围岩受到的破坏极为严重，甚至塌落至地表。这可能是因为土体颗粒的摩擦系数取值太小、地层的稳定性较差以及开挖面处于无支护状态的缘故。

2　细观参数对开挖面稳定性的影响

2.1　土体颗粒摩擦系数的影响

取不同土体颗粒摩擦系数fr时盾构隧道开挖面及地层变形和破坏情况如图8所示。由图8可知，当土体颗粒摩擦系数较小时，围岩坍塌范围和地层变形及地表沉降均很大；当土体颗粒摩擦系数较大时，围岩坍塌范围、地层变形及地表沉降则很小。

图8　不同摩擦系数下的地层变形

不同摩擦系数下的地层坍塌轮廓线如图9所示。由图9可知，地层坍塌轮廓和地表沉降随土体颗粒摩擦系数的增加而减小；土体颗粒摩擦系数越小，地层坍塌轮廓越大，开挖面破坏程度越严重。

模拟计算过程中对地表各点(A～I)的竖向位移进行监测。假定模型右侧边墙为横坐标轴x=0的界面，则不同摩擦系数下的地表沉降槽分布如图10所示。由图10可知，土体颗粒摩擦系数越小，地表沉降槽的形状越深。当土体颗粒摩擦系数逐渐增大到2.4时，地表沉降槽曲线趋于平缓，地表竖向位移较小，表明地表受到开挖面的影响较小。

图9　不同摩擦系数下的地层坍塌轮廓线

图10　不同摩擦系数下的地表沉降槽

2.2　土体颗粒接触模量的影响

假定土体颗粒摩擦系数为0.8，土体颗粒接触模量Ec分别为70，80，90，100，110和120 MN·m-1时，地表沉降槽的分布情况如图11所示。

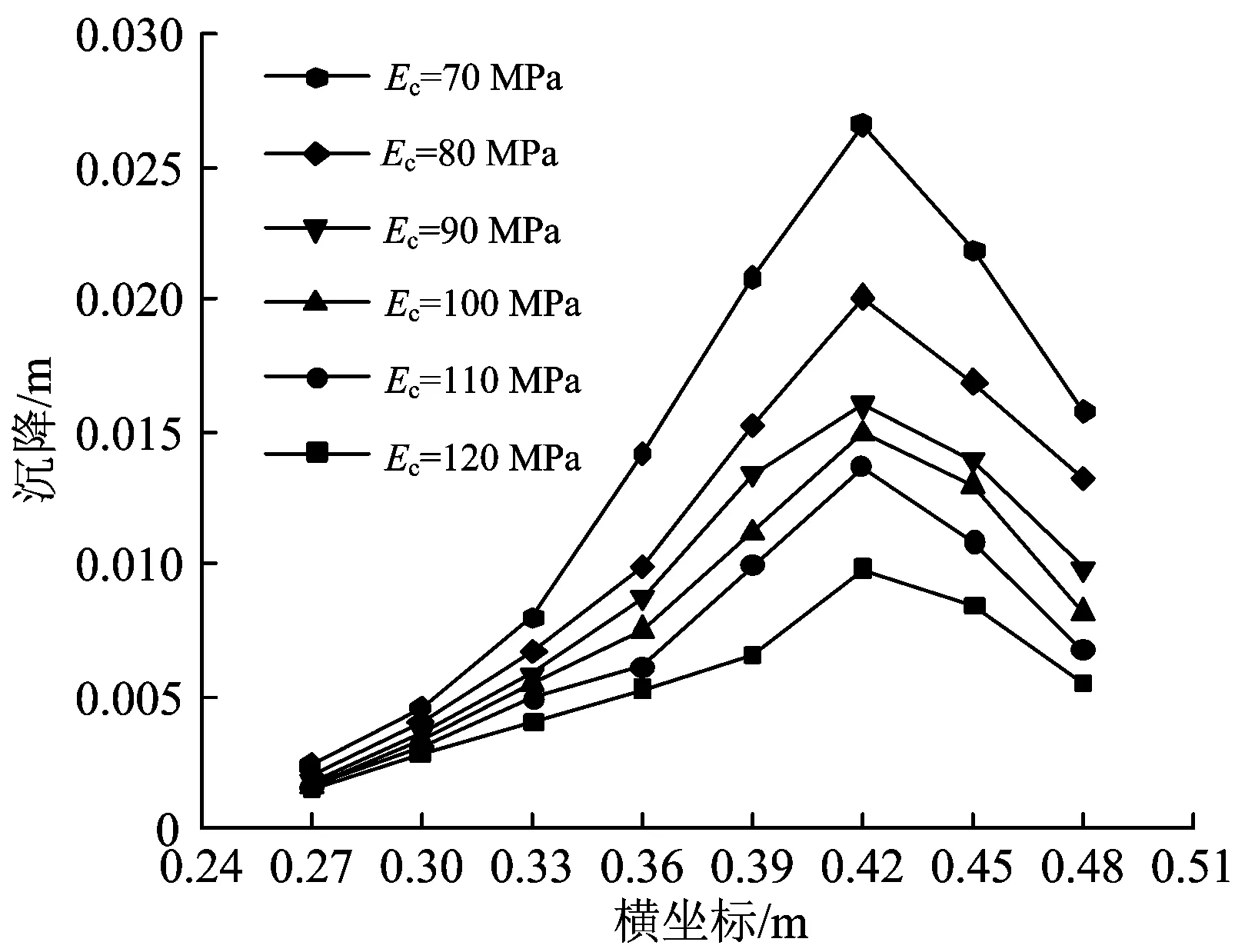
图11　不同接触模量下的地表沉降槽

由图11可知，不同接触模量下地表沉降槽的分布形态与图10的基本一致，坍塌轮廓范围和地层变形(包括地表沉降)随土体颗粒接触模量的增大而减小。当土体颗粒接触模量逐渐增大到120 MN·m-1时，地表沉降槽曲线趋于平缓，表明此时地表受到开挖面的影响程度较小。

3　泥膜对开挖面稳定性的影响

3.1　泥膜厚度的影响

泥膜由微细的黏结土体颗粒构成，其半径为0.5～0.8 mm。土体颗粒间采用接触黏合模型，法向黏合强度和切向黏合强度均为5 kN·m-1。在隧道开挖面处设置泥膜，泥膜厚度为5～30 mm，每隔5 mm设定为1种工况。典型的理想状态泥膜的颗粒流模型如图12所示。

图12　开挖面形成的泥膜

不同泥膜厚度下开挖面的挤出变形情况如图13所示。在黏合强度相同的条件下，开挖面挤出变形随着泥膜厚度的增加而减小；泥膜厚度越薄，开挖面挤出变形越显著，使开挖面破坏更严重，极易引起较大范围的地层变形，甚至导致地表塌陷。

图13　不同泥膜厚度下开挖面挤出变形

泥膜厚度为5～15 mm时，开挖面中心的挤出变形和地表沉降均不收敛，这表明由于泥膜厚度较薄而无法保证开挖面的稳定；根据数值结果可知，当泥膜厚度为20 mm时，开挖面挤出变形与地表下沉均可收敛，说明只有泥膜厚度达到某一量值时，开挖面的稳定方可保证。开挖面中心挤出变形与泥膜厚度的关系曲线如图14所示。

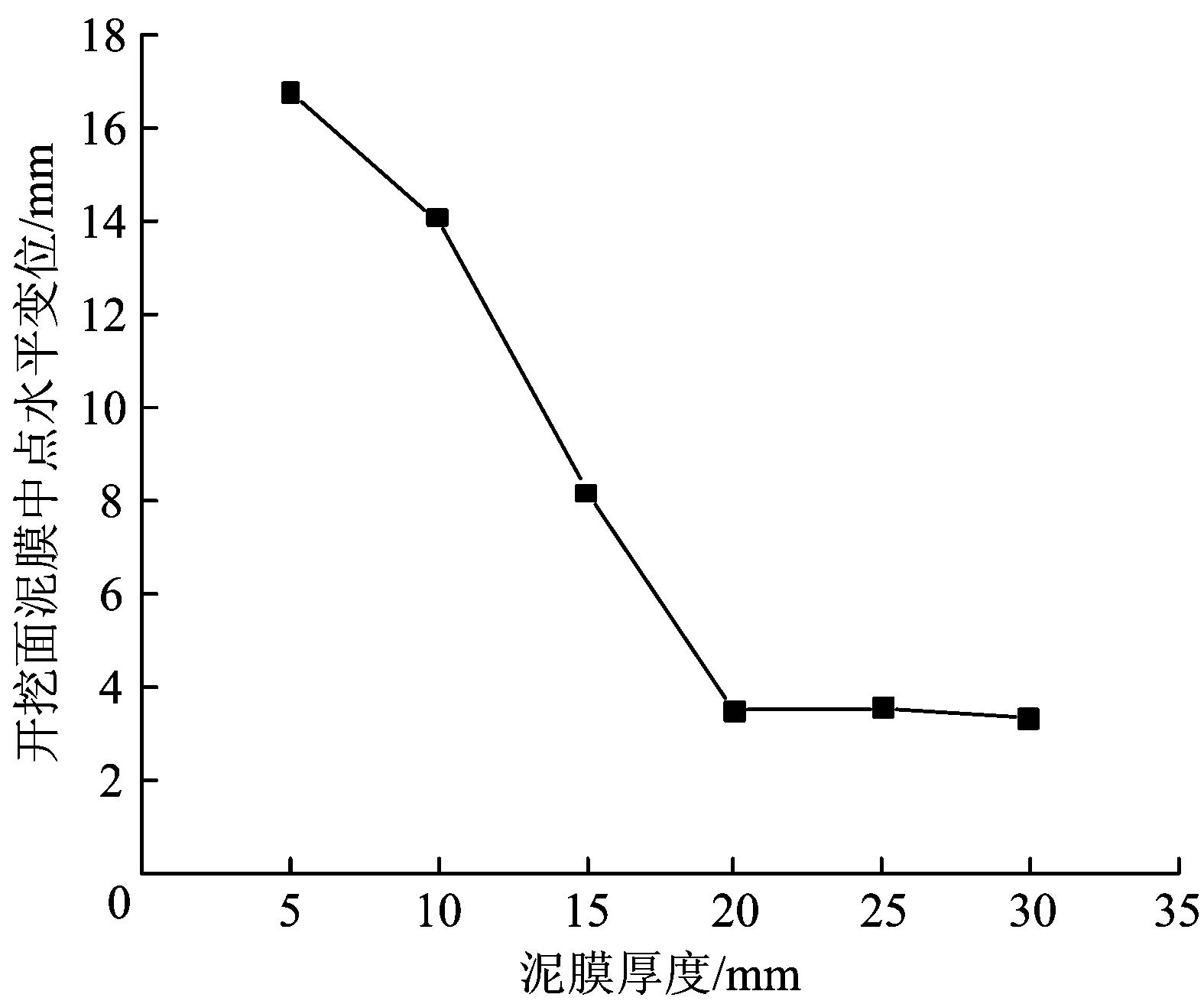
图14　开挖面中心挤出变形与泥膜厚度的关系

3.2　泥膜黏合强度的影响

不同泥膜黏合强度(1 000，1 400，1 800，2 200，2 600，3 000，3 400 N·m-1)条件下泥膜的变形和破坏情况如图15所示。由图15可知，在泥膜厚度相同的条件下，开挖面挤出变形随着泥膜黏合强度的减选而增大；当泥膜黏合强度很小时，开挖面挤出变形显著，泥膜破裂并出现坍塌现象，极易引起较大的地层变形。

图15　不同泥膜强度下开挖面变形

开挖面中心挤出变形与泥膜强度的关系曲线如图16所示。由图16可知，当泥膜黏合强度为1 000 N·m-1时，开挖面中心挤出变形和地表沉降均不能收敛；当泥膜黏合强度为1 400 N·m-1时，开挖面中心挤出变形和地表沉降趋于收敛；当泥膜黏合强度等于和大于1 800 N·m-1时，开挖面中心挤出变形和地表沉降已经可以完全收敛，可以保证开挖面的稳定。

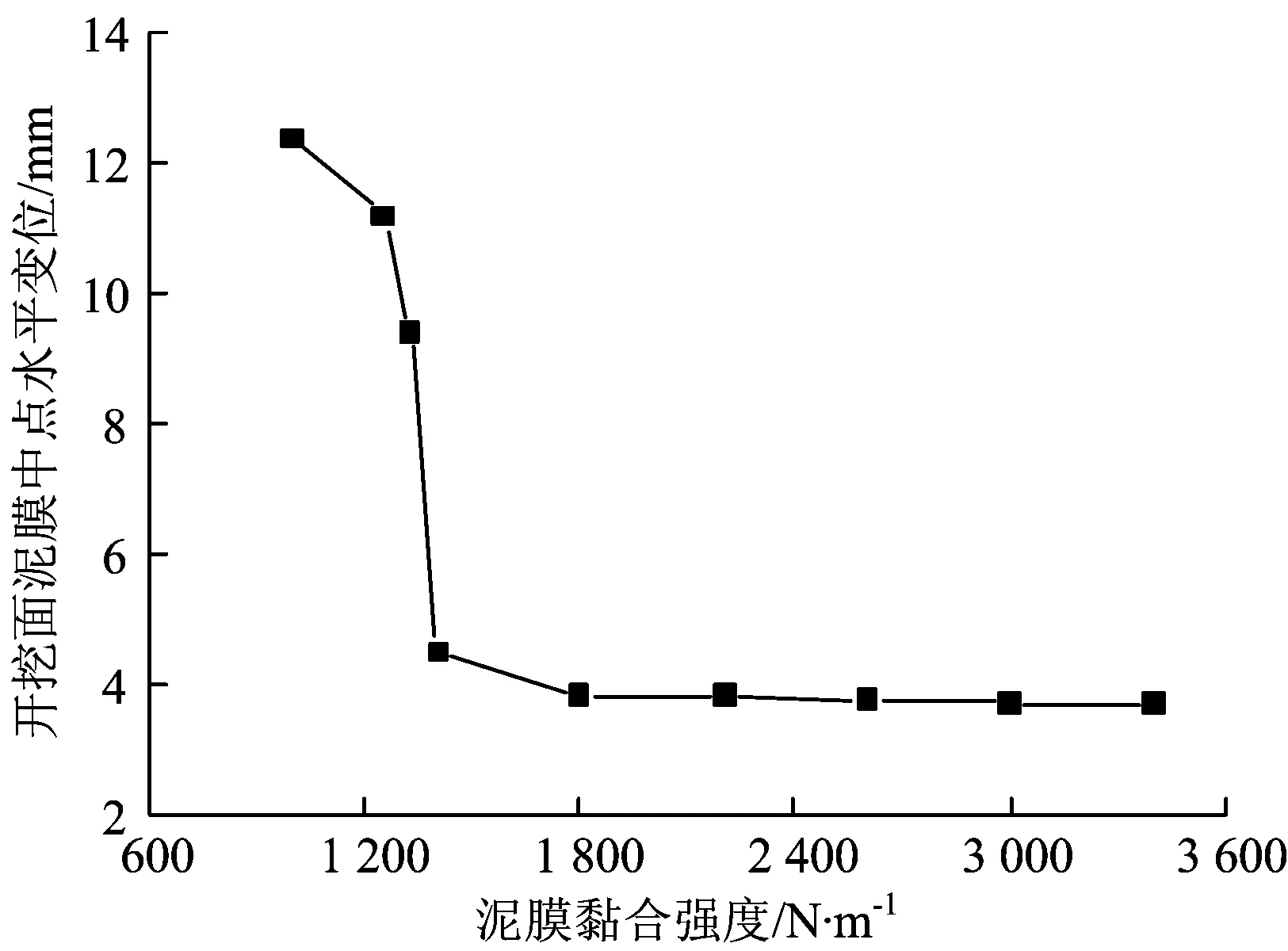
图16　开挖面中心挤出变形与泥膜黏合强度的关系

3.3　泥水盾构泥膜的渐进破坏过程

当泥水盾构泥膜的厚度为20 mm以及泥膜黏合强度为1 330 N·m-1时，不同运算步数条件下开挖面的挤出变形和渐进破坏过程如图17所示。在计算过程中，开挖面挤出变形和地表下沉不断增加，泥膜出现破裂。由于泥膜黏性较大，开挖面处的泥膜表现为块状坍塌的形态。泥膜完全破坏后，地层变形十分显著。

图17　开挖面挤出变形及渐进破坏过程

开挖面中心挤出变形和地表沉降历时曲线如图18和图19所示。由图18和图19可知，随着运算步数的增加，开挖面中心挤出变形和地表B，C和D点(见图9)的沉降逐渐增大，直至开挖面发生坍塌破坏。

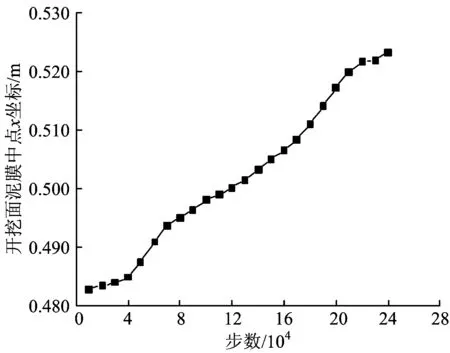
图18　开挖面中心挤出变形历时曲线

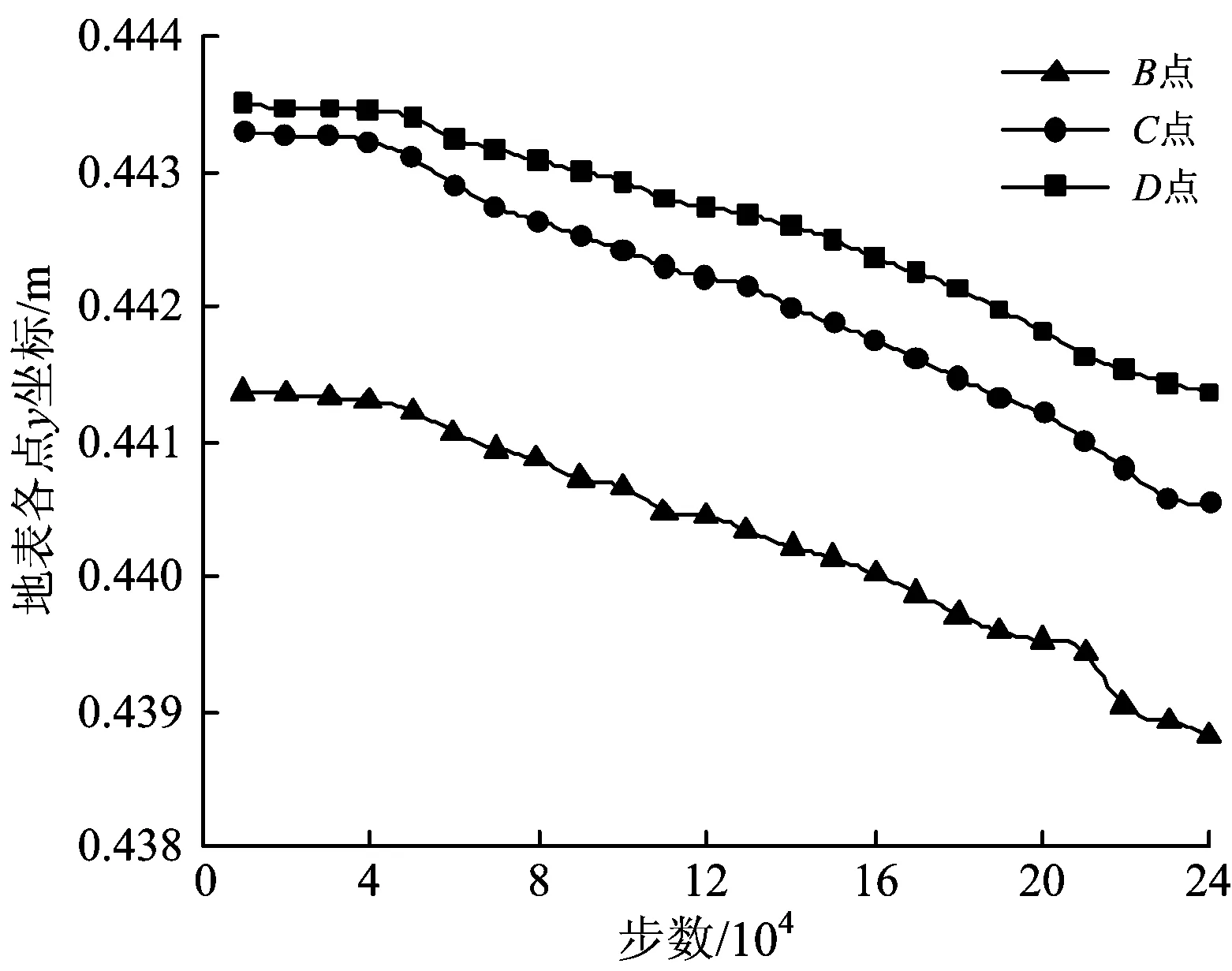
图19　地表沉降历时曲线

4　结　论

(1)开挖面在无支护状态下，开挖面土体发生应力松弛，土体颗粒向外鼓出和滑落，地层损失逐渐增大，导致开挖面前方土体发生破坏，进而引起地表塌陷。

(2)土体的颗粒摩擦系数和颗粒接触模量越小，地层坍塌轮廓越大，地表沉降槽越深，开挖面破坏越严重；反之，地层坍塌轮廓越小，地表沉降槽越浅。

(3)泥膜厚度和泥膜黏合强度对开挖面的稳定性影响显著。当泥膜厚度达到20 mm以及泥膜黏合强度达到1 400 N·m-1时，能够保证开挖面的稳定。

(4)当未形成良好的泥膜时，开挖面挤出变形和地层沉降逐渐增大；当泥膜呈现出破裂和块状坍塌等形态时，会产生较大范围的塌落区，地表沉降也显著增大。

[1]LI Y, EMERIAULT F, KASTNER R, et al. Stability Analysis of Large Slurry Shield-Driven Tunnel in Soft Clay[J]. Tunneling and Underground Space Technology, 2009, 24(4): 472-481.

[2]ZHANG C P, HAN K H, ZHANG D L. Face Stability Analysis of Shallow Circular Tunnels in Cohesive-Frictional Soils[J]. Tunneling and Underground Space Technology, 2015, 50: 345-357.

[3]胡欣雨，张子新. 不同地层条件泥水盾构开挖面失稳状态颗粒流模拟方法研究[J]. 岩石力学与工程学报，2013, 32(11): 2258-2267.

(HU Xinyu, ZHANG Zixin. Research on Particle Flow Approach for Modeling Face Failure Mechanism in Slurry Shield Tunneling under Complex Ground Conditions[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(11):2258-2267.in Chinese)

[4]王明年，魏龙海，路军富，等. 成都地铁卵石层中盾构施工开挖面稳定性研究[J]. 岩土力学，2011, 32(1): 99-105.

(WANG Mingnian, WEI Longhai, LU Junfu, et al. Study of Face Stability of Cobble-Soil Shield Tunnelling at Chengdu Metro[J]. Rock and Soil Mechanics, 2011, 32(1): 99-105. in Chinese)

[5]时振昊. 基于离散元的土压平衡盾构开挖面稳定及地层损失机理分析[D]. 上海: 同济大学, 2013.

(SHI Zhenhao. Analysis of Face Stability and Ground Loss Induced by EPBM Tunneling with Discrete Element Method[D]. Shanghai: Tongji University, 2013. in Chinese)

[6]CUNDALL P A, STRACK O D L. A Discrete Numerical Model for Granular Assemblies[J]. Géotechnique, 1979, 29 (1): 47-65.

[7]汪成兵，朱合华. 隧道塌方机制及其影响因素离散元模拟[J]. 岩土工程学报，2008, 30(3): 450-456.

(WANG Chengbing, ZHU Hehua. Tunnel Collapse Mechanism and Numerical Analysis of Its Influencing Factors[J]. Chinese Journal of Geotechnical Engineering, 2008, 30(3): 450-456. in Chinese)

[8]朱伟，钟小春，加瑞. 盾构隧道垂直土压力松动效应的颗粒流模拟[J]. 岩土工程学报，2008, 30(5): 750-754.

(ZHU Wei, ZHONG Xiaochun, JIA Rui. Simulation on Relaxation Effect of Vertical Earth Pressure for Shield Tunnels by Particle Flow Code[J]. Chinese Journal of Geotechnical Engineering, 2008, 30(5): 750-754. in Chinese)

[9]ZHANG Z X, HU X Y, SCOTT K D. A Discrete Numerical Approach for Modeling Face Stability in Slurry Shield Tunneling in Soft Soils[J]. Computers and Geotechnics, 2011, 38(1): 94-104.

[10]缪林昌，王正兴，石文博. 砂土盾构隧道掘进开挖面稳定理论与颗粒流模拟研究[J]. 岩土工程学报，2015, 37(1): 98-104.

(MIU Linchang, WANG Zhengxing, SHI Wenbo. Theoretical and Numerical Simulations of Face Stability around Shield Tunnels in Sand[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(1): 98-104. in Chinese)

[11]郑刚，崔涛，姜晓婷. 砂土层中盾构隧道局部破坏引发连续破坏的机理研究[J]. 岩土工程学报，2015, 37(9): 1556-1571.

(ZHENG Gang, GUI Tao, JIANG Xiaoting. Mechanism of Progressive Collapse Induced by Partial Failure of Shield Tunnels in Sandy Soil[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(9): 1556-1571. in Chinese)

[12]胡欣雨，刘安洋. 复合地层泥水盾构开挖面失稳破坏宏微观机理[J]. 上海交通大学学报，2015, 49(7): 1067-1074.

(HU Xinyu, LIU Anyang. Face Failure Mechanism for Slurry Shield-Driven Tunnel in Layered Ground Condition—Coupling Macroscopic and Microscopic Aspect[J]. Journal of Shanghai Jiaotong University, 2015, 49(7): 1067-1074. in Chinese)

[13]HE C, FENG K, FANG Y, et al. Surface Settlement Caused by Twin-Parallel Shield Tunnelling in Sandy Cobble Strata[J]. Journal of Zhejiang University—SCIENCE A：Applied Physics & Engineering, 2012, 13(11): 858-869.

[14]腾丽，张恒. 盾构穿越砂卵石地层地表沉降特征细宏观分析[J]. 岩土力学，2012, 33(4): 1141-1150,1160.

(TENG Li, ZHANG Heng. Meso-Macro Analysis of Surface Settlement Characteristics during Shield Tunneling in Sandy Cobble Ground[J]. Rock and Soil Mechanics, 2012, 33(4): 1141-1150,1160. in Chinese)

[15]江英超，方勇，何川，等. 砂卵石地层盾构施工滞后沉降形成的细观研究[J]. 地下空间与工程学报，2015, 11(1): 171-177,265.

(JIANG Yingchao, FANG Yong, HE Chuan, et al. Study on Delayed Settlement Formation Induced by Shield Tunnel in Sandy Cobble Strata[J]. Chinese Journal of Underground Space and Engineering, 2015, 11(1): 171-177, 265. in Chinese)

[16]CUNDALL P A, STRACK O D L. Particle Code in 2 Dimensions[M].[s.l.]: Itasca Consulting Group, Inc, 1999.

[17]Itasca Consulting Group, Inc. PFC2DUsers Manuals [M]. 3.1 ed. Minneapolis: Minnesota, 2004.