基于输入电流正弦化的三相两相矩阵变换器控制策略*

许宇翔， 方明辉， 雷能玮

(1. 湖州师范学院 工学院， 浙江 湖州 313000；2. 南京航空航天大学 自动化学院， 江苏 南京 210016；3. 湖州师范学院 信息工程学院， 浙江 湖州 313000)

许宇翔1,2， 方明辉1， 雷能玮3

(1. 湖州师范学院 工学院， 浙江 湖州 313000；2. 南京航空航天大学 自动化学院， 江苏 南京 210016；3. 湖州师范学院 信息工程学院， 浙江 湖州 313000)

以实现输入电流正弦控制为目标，推导了系统两相输出电压调制函数表达式的约束关系。针对常规空间矢量调制策略下的扇区划分数量较多，提出了带中线拓扑结构的三相-两相矩阵变换器(3-2MC)新型扇区划分方式以减少到24种扇区。基于该扇区划分提出了新的空间矢量调制策略，分析了矩阵变换器在该控制策略下的工作模态，给出了具体调制算法与占空比的算式，分析并推导了3-2MC输出与输入电压利用率表达式。最后，用MATLAB/Simulink对系统模型进行了动态与静态仿真研究，结果验证了该调制策略的正确性和有效性。

电流正弦化； 三相-两相矩阵变换器； 扇区划分； 空间矢量调制； 电压利用率

0 引 言

矩阵变换器(Matrix Converter, MC)作为一种交-交直接变换器，具有正弦的输入输出波形、输入功率因数可调、能量可双向传输、功率密度大、可靠性高等优点，成为目前国内学者研究的热点[1]。日本富士电机公司推出了FRENIC-MXC矩阵式变换器[2]，安川电机成功研发的Varispeed AC和FSDrive-MX系列矩阵变频器用于电机驱动[3- 4]。近年来，国内外很多学者除了研究MC应用于电机驱动外，也开始关注MC在其他领域的应用，如独立发电系统[5]、并网发电[6]等，以上研究成果表明了MC具有良好的应用前景[7]。

目前，国内外针对M×N相MC研究主要集中在3-3MC，包括拓扑结构[8-10]、控制策略[11-13]、换流方式[14]及死区补偿[15]等方面的研究，而3-2MC作为MC的一种特殊类型研究较少。文献[16]对3-2MC的调制策略进行了详细讨论；文献[17-18]分别提出了3-2MC的空间矢量控制与双电压合成策略；文献[19]提出了3-2MC的滞环控制策略，该控制策略的运用能加快系统的动态响应，降低损耗、减小计算量及易于数字化实现；文献[20]提出了一种新颖的3-2MC结构，该结构减少系统开关管数量，并将该结构应用于两相感应电机驱动；文献[21]提出了一种改进型空间矢量调制策略，该策略能减少3-2MC的开关次数与开关损耗，提高了系统的效率。

本文首先以实现3-2MC输入电流正弦控制为目标，以能量守恒为基础，推导了输出电压调制函数表达式的约束关系，针对原有空间矢量调制策略下的扇区划分数量较多，提出了带中线拓扑结构的3-2MC新型扇区划分模式，将MC的输出扇区由6个扇区减少为4个扇区，因而使输入输出的扇区组合数由36种减少至24种，并基于该扇区划分改进了原有空间矢量调制策略，分析了MC在该控制策略下的5种工作模态，给出了具体调制算法与占空比的算式，分析并推导了3-2MC输出与输入电压利用率表达式。最后，本文采用MATLAB/Simulink对系统模型进行了动、静态仿真，结果验证了该调制策略的正确性和有效性。

1 输入电流正弦控制下的输出约束关系

3-2MC常见拓扑结构主要有三端输出和两端输出两种[19]。本文以三端输出双级式拓扑结构为研究对象。该拓扑结构有3个输出端, 输出侧两相负载共用1个公共端N,如图1所示。该结构的左侧包含了由6个双向开关管组成的电流源型整流，右侧由6个功率管及反并联二极管组成的3相电压源型逆变器，输入与输出侧均包含LC滤波器用以滤除谐波。

图1 双级式3-2MC拓扑结构图

设三相输入电压表达式分别为

(1)

假设输入侧为单位功率因数，只含有基波分量，则三相输入电流的表达式分别为

(2)

则输入功率Pi表达式为

(3)

设两相输出电压的调制波函数分别为

(4)

式中：m1、m2——两相输出逆变侧各自调制系数；

φ——输出两相的相位差。

输出电压表达式分别为

(5)

式中：Uo1、Uo2——两相输出侧电压幅值；

Upn——母线电压；

mr——整流侧调制系数；

γ——输入侧功率因数角。

为方便分析，忽略输出滤波器上的无功功率，只考虑MC输出的基波分量，两相输出侧功率分别为

(6)

MC母线侧无直流储能环节，忽略系统损耗，则输入功率Pi(t)等于两相输出功率之和，即Po1(t)+Po2(t)，根据式(3)、式(6)，以避免输出侧脉动功率使输入侧电流中引入谐波分量为目标，即输出总功率也需要约束为常量，输出电压调制系数与输出侧两相电压相位差满足式(7)：

(7)

式中：mi——逆变侧调制系数。

两相输出电压的调制波函数满足式(7)的约束关系时，MC的输入电流除开关频率次的谐波外，只含有基波分量，避免了输入侧引入较难滤除的低次谐波。

2 新型扇区划分及工作模态分析

2.1 新型扇区划分

双级式3-2MC输入侧为电流型整流，其旋转空间矢量示意图如图2所示。在任意扇区内，根据正弦定理可得其有效矢量占空比为

(8)

式中：θr——输入相电流空间矢量所在扇区内的扇区角。

图2 输入侧旋转电流Ir空间矢量调制示意图

文献[18]提出了输出侧6扇区的划分。为了简化扇区划分数量，减少计算时间，本文提出了输出4个扇区的划分方式。划分方式以调制波信号过零点为依据，其输出电压旋转空间矢量示意图如图3所示。对于任意扇区内，其有效矢量占空比为

(9)

式中：θi——输出电压空间矢量所在扇区内的扇区角。

图3 输出侧旋转电压Ui空间矢量调制示意图

输出为两相电压量，在一个开关周期内分开导通，共有4种有效矢量，将输出划分为4个扇区，而输入电流空间矢量将输入电流空间划分为6个扇区，因此任意时刻输入与输出存在24种扇区组合情况，当输入电流与输出电压旋转空间矢量处于各自的某扇区时，本文采用4个有效矢量时间和1个零矢量时间合成，则双级协同调制下的矢量占空比及矢量作用时间为

(10)

(11)

式中：Ts——开关周期。

2.2 新型扇区划分下3-2MC模态分析

以输入电流矢量位于第Ⅰ扇区，输出电压位于第Ⅱ扇区为例，一个开关周期内3-2MC的开关组合如表1所示。

表1 输入-输出Ⅰ-Ⅱ扇区对应的功率开关组合

由表1可知，3-2 MC在开关周期Ts时间内有5个工作模态：

(1) 工作状态0～T1时间内，三相交流电中a、b相向负载相1通入反向电流，负载相2能量保持不变；

(2) 工作状态T1～T2时间内，三相交流电中a、b相向负载相2通入正向电流，负载相1能量保持不变；

(3) 工作状态T2～T3时间内，三相交流电中a、c相向负载相1通入反向电流，负载相2能量保持不变；

(4) 工作状态T3～T4时间内，三相交流电中a、c相向负载相2通入正向电流，负载相1能量保持不变；

(5) 工作状态T4～Ts时间内，负载相1和2能量均保持不变，即此时整流与逆变级均处于零矢量状态，其中零矢量状态的选取以开关管切换次数最少为依据。

2.3 3-2MC电压利用率分析

由于式(10)中有效矢量占空比≤1，因此调制比需满足式(12)，即

(12)

式中：m——系统总的调制比，m=mi×mr，即总调制比m≤0.707。

由于本文所研究的是带中线的3-2MC，输出两相电压均为线电压，以下分析以输出相1为例，由式(5)推导得，输出电压与输入电压之间电压利用率如式(13)所示。

(13)

如图1所示，带中线的3-2MC两相输出电压均为线电压，即式(13)反映输入功率因数 cosγ=1 时，输出线电压与输入相电压之间的电压利用率关系式。

3 仿真分析

利用MATLAB/Simulink软件搭建了3-2MC的仿真模型，进行了动态与静态仿真研究。具体参数设置如表2所示。

表2 仿真参数

图4为输入侧扰动下(输入220V突变至150V)的输入电流波形。由图4(a)可知输入三相电流稳态时呈对称分布；当输入侧发生扰动时，以输出电压幅值作为反馈量，经过PI调节获得对总调制比m的控制实现输出幅值闭环，输入三相电流在较短时间内就能达到稳定。由图4(b)可知，输入电流与该相输入电压无论是稳态还是瞬态均能保持较高的功率因数。可见在本文所提控制策略下，MC不仅能保持高功率因数电能输入，还能使输入侧获得正弦电流。

图5为输入侧三相扰动下(由输入220V突变至150V)的输出电压波形。由图5(a)可知输出两相电压幅值与相位差均满足式(7)要求，两相电压稳态时正弦化程度高；当输入侧发生扰动时，输入两相电压在较短时间内也能达到稳定，无明显振荡。可见在本文所提控制策略下，MC输出电压正弦度高(THD≤1.82%)，同时在扰动下响应速度快。

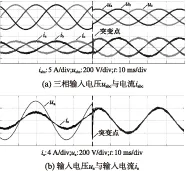
图4 输入侧扰动下的3-2MC输入仿真波形

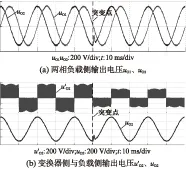
图5 输入侧扰动下的3-2MC输出仿真波形

图6为母线电压与电流波形。由于MC母线侧无大容量的储能元件，因此母线电压呈现二次输入电压频率的波动，但由于调制策略中采用了输出与输入级的协调控制，因此该波动并不会影响输出电压的质量。

图6 输入侧扰动下的3-2MC直流母线电流Ipn与电压Upn仿真波形

4 结 语

本文研究了以3-2MC输入电流正弦控制为目标的空间矢量控制策略，对原有扇区划分进行了改进，减少了扇区划分数量；以新的扇区划分为基础，提出了改进的空间矢量调制策略，分析并推导了3-2MC输出与输入电压利用率表达式。仿真结果表明，本文所提控制策略不仅使系统具有良好的稳态性能，而且动态响应快，能有效抑制动态过程产生的振荡，减少了输入电流的谐波含量。

[1] 孙凯，周大宁.矩阵式变换器及其应用[M].北京： 机械工业出版社，2007.

[2] ITOH J, SATO I, ODAKA A, et al. A novel approach to practical matrix converter motor drive system with reverse blocking IGBT[J]. Power Electronics, IEEE Transactions on,2005,20(6)： 1356-1363.

[3] YAMAMOTO E, HARA H, UCHINO T, et al. Development of mcs and its application in industry[J]. Industrial Electronics Magazine, IEEE,2011,5(1)： 4-12.

[4] SAWA T, KUME T, HARA H, et al. Power-electronics contributing to the green and clean world[C]∥Power Electronics and ECCE Asia (ICPE & ECCE), 2011 IEEE 8th International Conference on IEEE,2011： 11-18.

[5] 黄科元,贺益康,卞松江.矩阵式变换器交流励磁的变速恒频风力发电系统研究[J].中国电机工程学报,2002,22(11)： 100-105.

[6] 邓文浪,倪泽平.应用双级矩阵变换器的永磁直驱风力发电系统集成控制策略[J].太阳能学报,2012,33(4): 577-585.

[7] 张乔斌，夏益辉，朱爱芳.一种矩阵变换器驱动感应电机软起动方法[J].电机与控制应用，2014，41(9)： 62-68.

[8] ITOH J, TAKAHASHI H, HARUNA J. A high energy saving interface system using a matrix converter between a power grid and an engine generator for bio diesel fuel[C]∥Power Tech, 2011 IEEE Trondheim， IEEE, 2011： 1-7.

[9] KOLAR J W, BAUMANN M, SCHAFMEISTER F, et al. Novel three-phase AC-DC-AC sparse matrix converter[C]∥Applied Power Electronics Conference and Exposition, 2002， Seventeenth Annual IEEE, 2002： 777-791.

[10] 宋卫章,钟彦儒,孙向东.具有高电压传输比且能抵御非正常输入的Z-源双级矩阵变换器[J].中国电机工程学报,2010，30(24)： 21-28.

[11] WIJEKOON T, KLUMPNER C, ZANCHETTA P, et al. A predictive current control scheme for a hybrid AC/AC direct power converter[C]∥Power Electronics, Machines and Drives, 2006， The 3rd IET International Conference on IET,2006： 1-6.

[12] 张绍,周波,葛红娟.基于双空间矢量调制的矩阵变换器-永磁同步电机矢量控制系统[J].电工技术学报,2007,22(4)： 47-52.

[13] 史婷娜,刘立志,王慧敏,等.矩阵变换器-永磁同步电机驱动系统滑模变结构控制[J].电工技术学报, 2010,25(12)： 54-60.

[14] 佘宏武,林桦,王兴伟,等.基于电压型换流的矩阵变换器输出电压补偿方法[J].中国电机工程学报, 2011，31(3)： 20-27.

[15] 王勇,吕征宇,陈威,等.一种基于空间矢量调制的矩阵变换器死区补偿方法[J].中国电机工程学报, 2005,25(11)： 42- 45.

[16] KWAK S, TOLIYAT H A. Development of modulation strategy for two-phase AC-AC matrix converters[J]. Energy Conversion, IEEE Transactions on, 2005, 20(2)： 493- 494.

[17] 方永丽,谭国俊,董伟.三相-两相矩阵变换器的空间矢量调制策略及其实现[J].工矿自动化,2009,35 (11)： 50-53.

[18] FANG Y, ZHOU B, GAO X. A novel instantaneous value modulation method for two-phase matrix converter[C]∥Electrical and Control Engineering (ICECE), 2010 International Conference on IEEE, 2010： 3204-3207.

[19] MIRAZIMI M, SHARIFIAN M B B, BABAEI E. Hysteresis control of a three-phase to two-phase matrix converter[C]∥Power Electronics (IICPE), 2012 IEEE 5th India International Conference on IEEE, 2012： 1-5.

[20] MILAN G, MOHAMADIAN M, SEIFI E, et al. A novel minimized switch two-phase matrix converter for driving two-phase induction motor[C]∥Power Electronics and Drive Systems Technology (PEDSTC), 2012 3rd， IEEE, 2012： 7-12.

[21] LASKODY T, PRAZENICA M, KASCAK S. Space vector PWM for two-phase four-leg matrix converter[C]∥ELEKTRO, 2014, IEEE, 2014： 324-327.

Control Strategy of Three-Phase to Two-Phase Matrix Converter Based on Sinusoidal Input Current*

XUYuxiang1,2,FANGMinghui1,LEINengwei3

(1. School of Engineering， Huzhou University， Huzhou 313000， China； 2. School of Automation, Nanjing University of Aeronautics and Astronautics， Nanjing 210016， China； 3. School of Information Engineering， Huzhou University， Huzhou 313000， China)

Based on the sinusoidal control of the input current, the constraint relation of the three-phase to two-phase Matrix Converter (3-2MC) output voltage modulation function was derived. According to the conventional space vector modulation strategy, the sector was divided into a large number of sectors. A new type of sector partition method was proposed to reduce to 24 sectors. A new space vector modulation strategy was proposed based on the sector partition. The operating modes of the 3-2MC under the control strategy was analyzed, detailed modulation algorithm was given, got calculation formula of duty ration, and deduced the expression of 3-2MC voltage transfer ratio. Finally, simulation results confirmed the effectiveness and feasibility of the new control method.

sinusoidal input current; three-phase to two-phase matrix converter; sector partition; space vector modulation(SVM); voltage transfer ratio

湖州师范学院校级科研资助项目(2015XJLK35)

许宇翔(1981—)，男，硕士研究生，研究方向为新型变换器及其控制技术。

TM 301.2

A

1673-6540(2017)02- 0041- 06

2016-03-09