基于博弈论的物流园区开发模式

邱小平，赖苗

(西南交通大学交通运输与物流学院，四川成都 610031)

基于博弈论的物流园区开发模式

邱小平，赖苗

(西南交通大学交通运输与物流学院，四川成都 610031)

针对物流园区的2大投资主体——政府和企业，利用博弈论中合作博弈，构建政府与企业、企业与企业的博弈模型。在企业与政府博弈模型中采用完全信息静态博弈求得纳什均衡。在企业与企业的博弈模型中利用合伙人博弈模型，计算出两者的反应函数，寻找纳什均衡。结果表明：政府和企业共同投资物流园区是共赢的选择；若2家企业合作投资建设物流园区，投资比例为1:1时能使双方收益最大，且两家企业合作投资的协同程度越高，他们各自的收益函数值就越大。研究结果能为投资者提供决策依据。

物流园区；开发模式；博弈论；政府；企业

为了适应新常态经济的发展，物流园区对经济发展的极大促进作用逐步得到重视。截至2015年，物流园区达到1 210家，比2012年增长了60.5%[1]。

针对物流园区选址、园区规划、园区功能布局及园区的运营管理模式，学者们进行了广泛研究。文献[2]研究珠三角物流园区建设与区域经济发展之间的关系；文献[3]应用风险管理理论对物流园区的选址风险进行分析；文献[4]应用遗传算法构建园区内部功能区的布局模型，采用博弈论思想对布局方案进行评价；文献[5]基于PCA-DEA模型的物流园区绩效评价模型，对物流园区的运营绩效进行定量评价；文献[6]定义物流园区的运营模式，设立入驻企业选择体系，指导园区招商活动；文献[7]对物流园区的运营管理模式进行设计，指出物流园区的运营管理应坚持政企分开、市场化运作与企业化管理的原则。

目前针对园区的开发模式研究的较少。物流园区的投资建设具有投资金额巨大，资金回收期长、投资见效慢的特点，投资主体一般为政府与实体雄厚的企业[8]。由于缺乏专业人才以及投资积极性，开发模式以政府为主导的物流园区出现盈利能力弱、投资资金难以回收的状况。建设物流园区，不仅要为企业带来收益，还应该符合当地经济的规划，带动当地经济的发展，增加就业率，这在以企业为主导开发模式的物流园区很难保证[9]。若政府和企业两者共同投资开发物流园区，需要既保证园区的公益性又保证企业的盈利，基于此，本文采用博弈论构建博弈论模型进行分析。

1 博弈模型的构建及分析

博弈现象表面上是双方决策结果的对决，根本层次上是双方利益诉求的搏斗与较量，因为双方由决策引发的行动结果直接对应着各自的利益[10]。政府投资物流园区建设一方面是为了带动当地经济的发展，增加国民经济收入，促进就业；另一方面是为了发挥政府作为服务机构的职能——保证园区的公益性，服务公众。而企业是以盈利为目的的组织，其决策是为了实现自身利益最大化[11]。政府和企业在进行物流园区投资决策时都是理性的。

参与者的行为是相互影响的[12]。投资主体的决策在实现利润均衡的基础上达到各自利益的最大化。对于政府，它在决策是否投资物流园区时不仅要考虑对当地经济的推动及对就业率的影响，还要考虑对当地税收的影响[13]；而企业在进行投资开发园区决策时，政府的投资意向也会影响企业的投资意向，如影响土地审批、投资金额；如果2个企业共同投资，一个投资主体的投资决策将影响另一个投资主体的决策及收益。以博弈理论为工具，分析物流园区开发模式投资主体之间的选择行为，在博弈中寻求均衡。

1.1 政府与企业之间的博弈

1.1.1 假设

1)根据投资及不投资2种策略，则将博弈类型定为完全信息静态博弈[14]；

2)假设参与者都是理性的，做出的决策都是为了追求自身利益最大化；

3)假设参与者投资的比例与所获得收益的比例相同。

1.1.2 参数设定

1)当政府和企业同时选择投资策略时，政府的投资比例为ε，则企业的投资比例为(1-ε)，那么政府的收益为ε(I-c)，企业的收益为(1-ε)(I-c)，其中I为物流园区建成后的收益，c为开发物流园区所投入的资金，ε∈(0，1)。

2)当政府选择投资而企业不投资，则政府与企业的收益分别为θI-c、θI。其中θ为一方投资而另一方不投资对收益的影响系数，θ∈(0，1)。

3)当政府不投资而企业投资时，则政府与企业的收益分别为αI、(1-α)I-c，其中α为企业建设物流园区后盈利所上缴的税金系数，α∈(0，1)，且α<ε，结合我国企业税率，所以取α≤30%。

4)政府和企业都选择不投资物流园区，则它们的收益都为0。

1.2 企业与企业之间的博弈

鉴于物流园区初始投资资金多、资金回收慢、建设期长的特点，目前国内很多地区(尤其是二线城市)缺乏实力雄厚的物流地产商，若两家企业组成合伙人关系，共同投资建设园区[15]，协调企业资源，期望能降低单个企业开发园区的风险，使合作双方获得较大的收益。

企业投入园区建设的资金是该博弈过程中的策略，记为Si，策略组合为[0，1]，且策略可为0～1的任意实数。物流园区总的收益函数为：

F=(S1+S2+γS1S2),

(1)

式中：S1为企业1的投资策略；S2为企业2的投资策略；γ为2个企业间合作的协同参数，且γ∈[0，1]；γS1S2为企业1、2两者合作投资带来的协同效益。

协同指的是复杂系统的各分系统之间在操作运行过程中为了达到和谐统一的合作、协调、同步和互补[16]。本文指投资建设物流园区，2个投资主体利用各自的优势为更好、更快地建成物流园区在各方面的配合程度。如一家企业拿到政府的土地优惠政策，而另外一家企业信用较好享受到贷款政策等，两家企业合作，合理配置资源，共同建设物流园区。

企业1、2的收益函数F1、F2[17]分别为：

F1=ρ(S1+S2+γS1S2)-S12，

(2)

F2=(1-ρ)(S1+S2+γS1S2)-S22，

(3)

式中：ρ为企业1占收益的比例，ρ∈(0,1);(1-ρ)为企业2占收益的比例。

有这样一种均衡，在这一均衡中，在给定其他参与人战略决定的情况下，每个博弈参与人都确信自己选择了最优策略，从而使自己效用最大化。所有参与人的策略构成一个策略组合，这种策略组合称为纳什均衡。即在给定别人策略的情况下，没有人有足够理由打破这种均衡。在本文中，要找出企业1、2在投资园区中的纳什均衡，就是对企业1和企业2的收益函数分别进行一阶求导，即对式(2)(3)分别进行一阶求导，得

(4)

(5)

对式(4)(5)进行二阶求导，得

-2<0,

说明收益函数存在极大值[18-21]。

(6)

(7)

家庭在青少年的成长过程中有着重要地位，是预防青少年犯罪的第一道防线。但是，在互联网高速发展的今天，一些家长的“网络素质”显然跟不上发展要求，他们不知如何对孩子进行网络教育，缺少对孩子的网络引导，导致孩子受外界不良因素影响，最终走上犯罪的道路。

联立式(6)(7)，得出投资的纳什均衡为：

(8)

(9)

2 模型分析

2.1 政府与企业之间的博弈模型

由1.1.1可以看出该博弈的策略空间集合为{(投资，投资)，(投资，不投资)，(不投资，投资)，(不投资，不投资)}。

1)当企业采用的策略为投资时，政府可以获得收益ε(I-c)或αI。结合现实，政府会对新成立的物流园区自经营日起5 a内实施免征企业所得税，期满后5 a内减税，按15%征收企业所得税，则αI为0或者0.15I。当ε(I-c)≥αI时，则政府在投资园区中获得的收益大于园区上缴的税金。那么政府的最优反应是选择投资；当ε(I-c)<αI时，则政府的最优反应是不投资物流园区。

2)当企业采用的策略为不投资时，政府可以获得的收益为θI-c或0，θI-c>0，即政府的最优反应是投资物流园区。

3)当政府采用投资策略，企业采取投资的收益为(1-ε)(1-c)，企业采取不投资的收益为θI。若(1-ε)(I-c)>θI，则企业的最优反应是采用投资策略；若(1-ε)(I-c)<θI，则企业的最优反应是采用不投资策略。

4)当政府采用不投资策略，企业的收益为(1-α)I-c或0，则企业的最优反应是选择单独开发园区。

因此政府与企业有3个较优反应策略集合分别为(投资，投资)、(投资，不投资)，(不投资，投资)。即政府和企业共同投资开发物流园区以及政府或企业主导开发物流园区。

2.2 企业与企业之间的博弈模型分析

1)γ=1,ρ分别取不同值

ρ分别取0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9、1.0。将γ、ρ分别代入式(8)(9)，计算出纳什均衡下的投资资金S1*、S2*，即为最优的投资金额，再将纳什均衡下的投资资金(这时S1=S1*、S2=S2*)分别代入式(1)～(3)中，分别计算出最优的投资金额下企业1、2及物流园区的收益函数值，计算结果如表1所示。

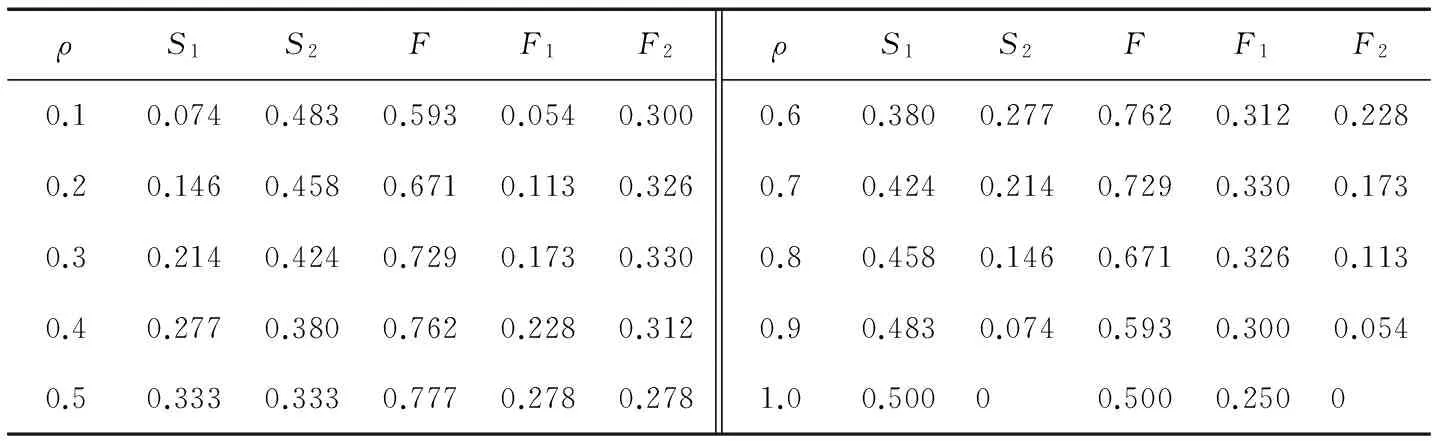
表1 γ=1,ρ分别取不同值的模型分析结果

从表1可以看出：

①企业1的收益。当ρ<0.7时，企业1获得收益的比例越大，即它投入的资金就越多，获得的收益也越大，而相应地企业2获得的收益就越小；当ρ=0.7时，企业1收益函数的值达到峰值，即0.330，此时，企业1所得收益最大；当ρ>0.7时，企业1的实际收益函数反而逐渐减小。这是由于企业1投入资金增加，承担相应的风险增大，获得的收益变小了。

②企业2的收益。当ρ=0.3，即1-ρ=0.7时，企业2收益最大，ρ<0.3时，即1-ρ>0.7时，企业2投入的资金越多，收益反而越少。

两家企业都想使自己的收益比例为0.7，当一家企业的收益比例为0.7时，则另一家的收益比例则为0.3。在两家企业投资资金都充足的情况下，二者为了促成合作，并使自己利益最大化，最终会走向收益占比为0.5的情况，即两家企业的投资比例为1:1。若有1家企业的资金略少，根据它的资金情况，可以考虑3:7和4:6的投资比例。

③物流园区的收益。当ρ<0.5时，F随着ρ的增大而增加，当ρ=0.5时，F取得最大值，随后，随着ρ的增大F变小。换句话说，当两家企业的投资比例为1:1时，物流园区的总体效益函数F达到极大值。

2)ρ=0.5,γ分别取不同值

γ分别取0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9、1.0。ρ=0.5为物流园区的纳什均衡，设ρ=0.5，讨论两个企业的协同参数γ对双方收益的影响。同理，通过式(1)～(3)(8)(9)计算最优投资金额下企业1、2及物流园区的收益函数值，计算结果如表2所示。

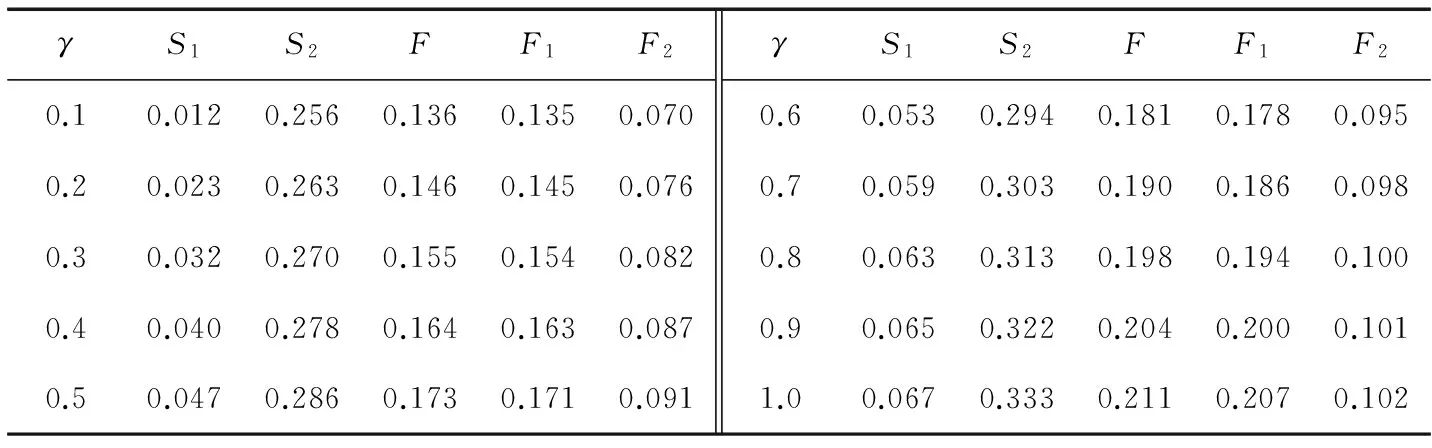
表2 ρ=0.5,γ分别取不同值的模型分析结果

从表2可以看出:随着γ的增加，3个收益函数值都呈增长趋势，且总体收益函数F大于2个企业单独的收益。两家企业合作投资的协同程度越高，他们各自的收益函数值就越大。合作投资不仅能够降低企业投资风险，有利于增加企业个体的收益，而且能大大增加物流园区的整体收益。

3 案例分析

绵阳市某物流园区由政府和企业共同投资开发建设，项目总投资为6.6亿元，其中企业计划投资3.6亿元，向政府申请财政支持3亿元，预计建成后年收益可达到1.2亿元。利用政府与企业博弈模型进行分析。

政府投资比例ε=0.45，企业的投资比例为0.55，θ=0.9，α=0.3。

1)当企业选择投资时，政府有投资和不投资2种决策。计算得政府投资的收益为0.499 5、不投资则为0.36，故政府选择投资；

2)当企业选择不投资时，政府投资的收益为0.882 0，不投资的收益为0，故政府选择投资；

3)当政府采取投资策略时，企业投资的收益为0.600 6，不投资收益为0.12，因此企业选择投资；

4)当政府采取不投资策略时，企业投资的收益为0.642 0，不投资收益为0，因此企业选择投资。

因此纳什均衡为(投资，投资),即(0.499 5，0.600 6)，策略组合总值为1.1001。即政府和企业共同开发物流园区总收益最大。该结论与上述模型分析结果吻合。

该物流园区选择政府和企业共同开发的模式，一方面能降低自身风险，使各自利益最大化，另一方面，使物流园区的总体利益最大化，(投资，投资)策略即(0.499 5，0.600 6)组合总值1.100 1大于其他3个策略组合，且双方共赢。因此选择政府和企业共同投资开发模式是确实可行的。

4 结语

从博弈论的角度对物流园区的投资开发模式进行研究，并结合实际案例进行分析。政府和企业共同投资物流园区是切实可行的；若两家企业合作投资物流园区，且两家企业资金相当，投资比例为1:1时能使双方收益最大。

[1]中国物流与采购联合会，中国物流学会.第四次全国物流园区(基地)调查报告[R].北京:中国物流与采购，2015.

[2]董明伟.基于系统动力学的珠三角物流园区建设与区域经济发展关系研究[D].广州：华南理工大学，2012. DONG Mingwei.Research on the interaction of logistics park construction and area economy in pearl river delta based on system dynamics[D].Guangzhou:South China University of Technology，2012.

[3]沈姗姗.物流园区的选址风险分析[D].武汉：武汉理工大学，2006. SHEN Shanshan.The risk of distribution park location[D].Wuhan:Wuhan University of Technology，2006.

[4]王叶青.物流园区内部功能区布局规划实证研究[D].杭州：浙江工商大学，2010. WANG Yeqing.Empirical study on the layout planning for the function areas in logistics park[D].Hangzhou: Zhejiang Industry and Commerce University，2010.

[5]冯小静.基于PCA-DEA的物流园区绩效评价研究[D].西安：长安大学，2012. FENG Xiaojing.Research of logistics park′s performance evaluation on PCA-DEA model[D].Xi′an:Chang′an University，2012.

[6]张道臣.物流园区运营模式研究[D].北京：北京交通大学，2009. ZHANG Daochen.Study on the operation mode of logistics park[D].Beijing:Beijing Jiaotong University，2009.

[7]韩兰兰.物流园区运营管理模式研究[D].西安：长安大学，2010. HAN Lanlan.Study on the operation and management mode of logistics park[D].Xi′an:Chang′an University，2010.

[8]何黎明.中国物流园区[M].北京:中国物资出版社，2009:17-18.

[9]戴航，何景师，张培林，等.基于博弈论的物流园区投资开发模型研究[J].物流技术，2014，33(3)：86-88. DAI Hang，HE Jingshi，ZHANG Peilin,et al.Study on investment and development model of logistics parks based on game theory[J].Logistics Technology，2014，33(3)：86-88.

[10]于斌斌，余雷.基于演化博弈的集群企业创新模式选择研究[J].科研管理，2015,36(4)： 30-38. YU Binbin，YU Lei.A study on cluster enterprise technology innovation selection based on the evolutionary game[J].Research Management，2015，36(4)：30-38.

[11]戴航.基于博弈分析的物流园区运营模式研究[D].武汉：武汉理工大学,2010. DAI Hang.Study on the operating model of logistics park based on the game theory[D] Wuhan: Wuhan University of Technology,2010.

[12]张维迎.博弈论与信息经济学[M].上海：上海人民出版社，2004.

[13] GUAN Y.Resource curse,economy transform and government function change[J].Economic Survey，2013，1(1)：77-81.

[14]张金灿，仲伟周.碳税最优税率确定的完全信息静态博弈分析[J].中国人口资源与环境，2015，25(5)：53-58. ZHANG Jincan，ZHONG Weizhou.Static game analysis with complete information about the optimal carbon tax rate[J].China Population，Resources and Environment，2015，25(5)：53-58.

[15]胡正东，李夏苗，李利华，等.合作博弈下医药物流联盟节点决策模型及算法[J].计算机工程与应用，2012，48(20)： 32-38. HU Zhengdong，LI Xiamiao，LI Lihua，et a1.Model and algorithm for nodes decision of medicine logistics alliance under cooperative game[J].Computer Engineering and Applications，2012，48(20)：32-38．

[16]张牛.要竞争也要协同[J].经营者， 1996，9(1)：17. ZHANG Niu.Not only need competition,but also reguire cooperation[J].Enterprise Marketing,1996,9(1):17.

[17]DUTTA P K.Strategies and games:theory and practice[J].Mit Press Books, 1999, 1(1):82-84.

[18]潘峰，西宝，王琳.基于演化博弈的地方政府环境规制策略分析[J].系统工程理论与实践，2015，35(6)：1393-1404. PAN Feng，XI Bao，WANG Lin.Analyis on environmental regulation strategy of local government based on evolutionary game theory[J].Systems Engineering-Theory & Practice，2015，35(6)：1393-1404.

[19]饶常林.中国地方政府合作的博弈分析:困境与消解[J].北京理工大学学报(社会科学版)，2014，16(5)：59-64. RAO Changlin.Game analysis of cooperation among local governments in china :dilemma and solution[J].Journal of Beijing Institute of Technology(Social Sciences Edition)，2014，16(5)：59-64.

[20]曹博洋，姜明辉.多种风险下研发项目投资决策博弈分析[J].运筹与管理，2015，24(5)：66-74. CAO Boyang，JIANG Minghui.R&D project investment decision game analysis under a variety of risk[J].Operations Research and Management Science，2015，24(5)：66-74.

[21]陈珠明，张天舒.战略配售股东的投资行为和最优减持策略[J].系统工程学报，2015，30(5)：659-670. CHEN Zhuming，ZHANG Tianshu.Analysis of the investment behavior and optimal trading policy of strategic allotment shareholders[J].Journal of Systems Engineering，2015，30(5)：659-670.

[22]李韶庭.深圳东西部港区保税物流博弈分析[D].北京：清华大学，2012. LI Shaoting.Game analysis of bonded logistics in shenzhen[D].Beijing:Tsinghua University，2012.

[23]周慧, 严以新. 港口企业双寡头价格质量博弈分析[J].河海大学学报(自然科学版), 2004, 32(4):470-473. ZHOU Hui,YAN Yixin.A port duopoly game model for price and quality competition[J].Journal of Hohai University(Natural Sciences)，204，32(4)：470-473.

(责任编辑：杨秀红)

Study on Development Model of Logistics Parks Based on Game Theory

QIUXiaoping,LAIMiao

(SchoolofTransportationandLogistics,SouthwestJiaotongUniversity,Chengdu610031,China)

For two major investment bodies of the logistics park-government and enterprise, the paper utilizes the cooperative game in Game Theory as a tool to build a Game model between the enterprise and government as well as among enterprises. In the Game model between enterprise and government, the static game of complete information is used to obtain the Nash equilibrium by using the method of marking. In the Game model among enterprises, the partner game model is used to calculate the reaction function and find the Nash equilibrium. The results show as follows. The logistics park invested by the government and enterprise is a win-win choice. If two enterprises cooperate with each other in the investment of the logistics park, the investment ratio of one to one can make the maximum profit and the cooperation of the joint investment of the two enterprises is stronger and the function value of their respective profit is bigger. So the research results can provide the investors with decision-making evidence.

logistics park; development model; game theory; government; enterprise

2016-07-22

邱小平(1976—)，男，四川南充人，工学博士，教授，主要研究方向为物流系统仿真与优化,E-mail:514826660@qq.com.

10.3969/j.issn.1672-0032.2017.01.007

F252.5；F224.32

A

1672-0032(2017)01-0040-06