Joint Spectrum Sensing Based on Variance and Correlation Analysis
2017-04-08JunshengMuXiaojunJingHaiHuangNingGao1LaboratoryofBiologicalRecognitionandInformationApplicationBeijingUniversityofPostsandTelecommunications
Junsheng Mu*, Xiaojun Jing Hai Huang Ning Gao1 Laboratory of Biological Recognition and Information Application, Beijing University of Posts and Telecommunications
2 Key Laboratory of Trustworthy Distributed Computing and Service, Ministry of Education, 100876, China
* The corresponding author:Junsheng Mu, email: mu_junsheng@126.com
I. INTRODUCTION
THE available spectrum resource becomes the thing of growing importance and scarcity with the global development of wireless communication services [1]. However, most of the registered spectrum is unoccupied in both time and space according to the investigation of Federal Communications Commission (FCC)[2]. Cognitive radio [3] is an intelligent radio technology with the capability to search and utilize underutilized spectrum resources.
Spectrum sensing (SS) [4] is the base of cognitive radio (CR) networks whose main purpose is to judge whether PU exists with the self-adapting monitoring and perception of secondary users (SUs), where the PU is the radio that has the permission of use the registered channel and SU is the unlicensed radio.The performance of sensing spectrum holes is evaluated by the detection probability and the probability of false alarm. A miss in the detection will cause the interference with PU and a false alarm will reduce the spectral efficiency.The optimal detection performance occurs in the case that the detection probability is maximized subject to the constraint of the false alarm probability. According to the standard of wireless regional area networks (WRAN)based on CR of 802.22 working group [5],the detection probability of propagable CR is at least for 90% while the probability of false alarm is below 10%. Practically, to the best of our knowledge, this is a hard work in the state of art considering the computational and implementation complexity.
Energy detector (ED) [6] is commonly accepted for SS due to its simple implementation and low complexity. However, its detection performance is vulnerable to uncertain noise,especially under a low signal to noise ratio(SNR). For a better detection performance,cooperative spectrum sensing is investigated based on the exploration of the spatial diversity in the observations of spatially located CR users, where SU can share their sensing information to make a combined decision more accurate than the individual decisions. Cooperative spectrum sensing (CSS) [7-8] includes the centralized and distributed sensing. The centralized SS works on basis of joint judgment of multiple SUs, where the individual decision or observation data is transmitted to a fusion center (FC) and the final decision is made in FC. In the distributed SS, the individual SU shares sensing information, and judge whether the radio band is busy alone. One of the most efficient methods for CSS is Majority voting(MV) [9], where the decision is made in FC based on the majority voting for the presence or absence of PU. Furthermore, the authors in [10] proposed an improved energy sensing(IED) method that was able to outperform the classical ED scheme while preserving a similar level of algorithm complexity as well as its general applicability, which was different from the CSS essentially.
In this paper, a novel method based on joint analysis of variance and correlation for spectrum sensing is proposed, where correlation between the primary signal and noise is taken into consideration.
Apart from ED, Cyclostationary feature detector (CFD) [11-12] and covariance based detector (CBD) [13-14] are also well known methods in SS. CFD detects and distinguishes between different types of primary signals by exploiting their Cyclostationary features.Due to the independence of the estimation of noise variance, CFD works well in low-SNR regimes. However, the advantages of CFD are rooted in that the mean and autocorrelation of a continuous time random process have a periodicity in time; Besides, the detection performance is at the expense of a higher computational cost. CBD appears for the issue of noise uncertain in ED. According to some latest random matrix theories (RMT) [15], the approximate distribution of the largest and smallest eigenvalues is determined, by which the closed-form solution of the detection probability and false alarm probability is derived based on the radio of maximum eigenvalue to minimum eigenvalue. Distinctly, CBD is a blind detector, insensitive to noise power.In this paper, we devote our effort to explore another blind detector with a lower computational cost compared with CBD.
In the literature, the general model in ED for SS is always established on three assumptions [6]: (1) The noise is a Gaussian, independent, and identically distributed (iid) random process with mean zero; (2) The primary signal is an iid random process with mean zero; (3) The primary signal is independent of noise. In practice, the received samples are the filtered outputs through a band-pass filter.As a result, the corresponding output samples may be correlated. Additionally, noise may not obey or not strictly obey Gaussian distribution in the real environment. Furthermore, the accurate grasp of channel gain function that belongs to a given PDF (Probability Distribution Function) is not an easy task. To overcome these shortcomings as far as possible, a blind detector based on the correlated channel model is in urgent need to be proposed.
In this paper, a joint spectrum sensing method based on the variance and correlation analysis (JSS) is proposed, starting with correlation factor and variance analysis of time frames for the correlated signal. After theoretical derivations, the product of correlation factor and variance with adjustment factors is considered as the criterion to decide whether PU exists. Besides, the corresponding detection thresholds are also designed, which changes adaptively in the wake of environment variation. The main contributions in this paper are concluded as the following:
1. Evaluate the sensing error of ED due to the ignorance of the correlation between the primary signal and noise together with uncertain noise power.
2. Present a novel blind sensing scheme based on joint analysis of correlation and variance.
3. Redesign detection thresholds.
Note that JSS is a novel blind detector based on the variance and correlation analysis,insusceptible to the estimation of noise variance and the wireless propagation channel.Therefore, it suffers little from noise uncertainty. On the other hand, JSS dramatically differs from the traditional CSS. JSS proposed in this paper is a single SU spectrum sensing method based on the joint analysis of variance and correlation, while CSS works on the cooperative sensing of multiple SUs. In addition,OFDM (Orthogonal Frequency Division Mul-tiplexing) signal [16] is treated in this paper as the PU signal. Using OFDM has the advantage to be able to feed certain sub-carriers with zeros resulting in no emission of radio power on these carriers (occupied by licensed users).The use of OFDM also enables the analysis of the spectral activity of licensed users at no extra cost, as an FFT is required anyway.
Simulation experiments show that the proposed method has a wider applicability and a stronger robustness, suitable for various channels including AWGN, Rayleigh, Rician.Furthermore, the detection performance is dramatically improved compared with the classical ED method.
The rest of this paper is organized as follows. Section 2 presents the primary principle of ED and exhibits sensing error due to the ignorance of the correlation between the primary signal and noise along with the uncertain noise power. The main contribution of this paper is shown in Section 3, which consists in a consideration of the correlation between the primary signal and noise. Simulation experiments and result analysis are accomplished in Section 4. Finally, Section 5 concludes this paper.
II. ERROR ANALYSIS OF ED
2.1 Error from the ignorance of the correlation between the primary signal and noise
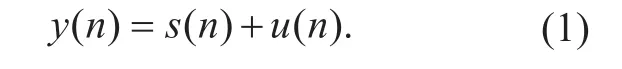
Usually, sn() and un() meet the following assumptions:
(a) un() is a Gaussian, independent, and identically distributed (iid) random process with mean zero and variance of value σu2.
(b) sn() is an iid random process with mean zero and variance of value σs2.
(c) sn() is independent of un().
Under the assumption H1that the PU is active, the probability of detection Pd(,)ετ[6] in circularly symmetric complex Gaussian(CSCG) noise case could be written as:
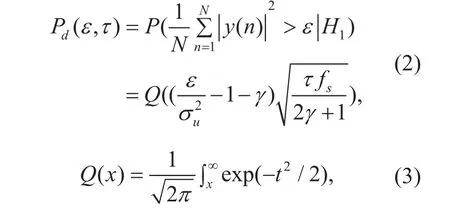
where τ is the sensing time, fsis the sampling frequency of SU, Nf=τsis the sampling number of SU, γ=σs2σu2and ε is the predetermined energy threshold.
Under the assumption H0that PU is absent, the probability of false alarm Pf(,)ετ[6]in CSCG noise case could be shown as:


where µ1,,ε1are the expectation, variance, energy threshold when there is a weak correlation between the primary signal and noise. On the side, ρ0denotes the correlation between the primary signal and background noise, which will be determined by Eq. 15-18.
The error ∆ε between ε and ε1is shown as:

where ∆ε results from the correlation between the primary signal and noise. In other words,f()ρsignoi−is the function of ρsignoi−(the correlation factor between signal and noise) that leads to ∆ε. As a result, the following conclusions are drawn,

If ε1>ε it indicates that both the detection and false alarm probability in the case ε=ε are higher than the case ε=ε1; if ε1<ε,it denotes that the detection and false alarm probability in the case ε=ε are both lower than the case ε=ε1. For ED, noise u(n)obeys Gaussian Distribution which is a bellshaped curve. As a result, an imperceptible change of energy threshold may have a great influence on the probability of detection and false alarm, the simulation result is just as shown in figure 1.
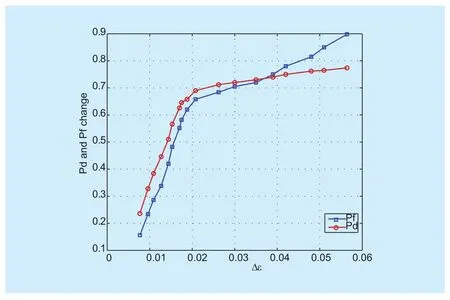
Fig. 1 The influence of De on detection probability and probability of false alarm(SNR=−10dB, signal type:OFDM)
In figure1, the simulation band is conducted at Very high frequency (VHF), where the carrier frequency is set as the sampling frequency of SU is 1.010;×8hz the sampling frequency fsof SU is 3.010×8hz. Considering the sensing time and detection performance simultaneously, N=100. In the simulation,the OFDM signal is firstly generated and then white Gaussian noise with mean zero and variance one is added into the OFDM signal. After the sampling and energy normalization of the noise-only case and the signal-plus-noise case,we calculate the detection and false alarm probability by the corresponding energy comparisons with the presupposed threshold.
We assume ∆ε as the threshold increment of ED and analyze the situation of the detection probability and the false alarm probability as ∆ε varies. The vertical axis of figure 1 denotes the increment of the detection probability and the false alarm probability as ∆ε increases.
From figure 1, when ∆ε varies from 0 to 0.06, both Pfand Pdnearly vary from 0 to 1,which declares a great influence will happen for the detection performance if the detection threshold varies subtly. While one possible reason for the subtle change of the detection threshold comes from the weak correlation between the primary signal and environmental noise, which is not taken into consideration for many classical ED based methods. Consequently, for an accurate detection performance,the correlation coefficient ρsignoi−between the primary signal and noise is a significant and indispensable element in ED.
2.2 Error from uncertain noise power
In an ED, the SNR rgfor a given Pf(,)ετ and Pd(,)ετ could be determined as

where N is the number of samples.
In signal processing, a phenomenon often occurs, defined as SNR wall [17-18], where there is a lower limit of the SNR beyond which it is impossible for ED to detect the presence of the PU signal. For an uncertain factor θ of noise power estimation, the noise variancevaries fromThe marginal stage of a SNR wall meets

Another expression of Eq.9 is shown as
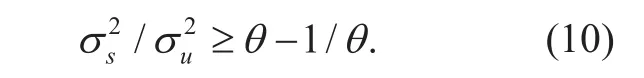
By virtue of Eq.10, the SNR wall could be expressed as

Due to the existence of SNR wall, the detection threshold ε denoted in Eq.2 and Eq.4 could be denoted as

Substituting Eq.12 into Eq.2, we can obtain

Substituting Eq.13 into Eq.2, the detection probability suffering from noise certainty could be exhibited as

From Eq.14, we can see how the noise uncertainty limits the operational deployment of ED as a CR in practice where perfect knowledge of noise power is uncertain.
III. THE PRIMARY PRINCIPLE OF JSS
As mentioned in Section 2, ED has an inaccurate threshold estimation and ignore the correlation between the primary signal and noise.Apart from that, ED method generally suits for AWGN Channel. For some uncertain channels(channel whose PDF is unknown), ED method could not work any longer. To search for a possible breakthrough of these disadvantages, JSS method is proposed for self-adapting spectrum sensing to suppose there is a PU signal that is correlated with the channel noise.
3.1 The main principle of JSS
JSS method starts with correlation factor and variance analysis of the observation signal.Suppose y(n)=[y(0),y(1),...,y(N −1)], the autocorrelation of y(n) could be written as,

To conduct eigenvalue decomposition [20]of T, the received eigenvalues are different mutually and the corresponding eigenvectors are orthogonal due to the symmetry of T. Every element in matrix T denotes the correlation of different time. As a result, the eigenvalues of T represent the correlation of its corresponding directions (eigenvectors). Generally,on the same scenarios that the received signal and background environment are constant, the correlation of signal to signalis larger than the correlation of signal to noise, and the correlation of signal to noise is larger than the correlation of noise to noiseThat isThe reason for this sorting is that the signal has some correlation between different frames for its continuity, while noise has little correlation for its randomness (nearly approaches to zero). These two cases work as the extreme conditions, resulting inin general for the same scenarios.
As a result, under the assumption H1the P largest eigenvalues has the maximum possibility to represent the correlation of the primary signal [21]. Under the assumption H0that the primary signal is absent, the M largest eigenvalues denote the correlation of noise to noise
It is noted that the correlation model has not been used for SS like this, while it is wide-ly applied in speech enhancement [20-21].One reason is that the correlation factor ρ seriously suffers from noise uncertainty in SS and cannot serve as a criterion with a better detection performance to determine whether PU exists, different from the case in speech enhancement that the correlation model is only used to reduce background noise. In this paper,both the correlation factor and variance are taken into account to work as a novel criterion for SS, which could remove noise uncertainty to a great extent according to our analysis in the following.

For removal of amplitude fluctuation as far as possible, the product of correlation factor and variance is considered as the criterion to determine whether PU exists. Generally, when the correlation factor of the primary signal ρsigturns greater , their amplitude fluctuation becomes smaller, resulting in a smaller variance Dsignoi−in return. Consequently, the amplitude fluctuation of the primary signal and noise have less influence on the product of correlation factor and variance.

Obviously, the proposed method has a distinct difference compared with the classical ED method. The JSS detects idle spectrum by means of the correlation factor and variance,while the classical ED method is based on the energy comparison between the received signal and a predetermined threshold. On the other hand, the JSS does not depend on the PDF of channels, which improves the applicability to environment. While for some channels that PDF is unknown or not accurately presented,ED based methods will cause much deviation.Furthermore, noise uncertainty is greatly removed in JSS, which will make a better detection performance in return.
3.2 Threshold estimation
In this subsection, the detection threshold is evaluated for self-adaption to the environment.

Suppose ρ.DM= when the PU is busy and ρ.DN= in the case that the radio frequency is idle. Based on Eq.22 and Eq.23, considering protecting PU and the achievable throughput for the secondary network, the threshold ε1in the ideal conditions should satisfy simultaneously the following restraints

In our experiment, α and β are both fi xed as 0.2 for convenience. Then (27) could be simplified further as

Therefore, a reasonable threshold scheme is shown based on (28) and the statistics of our experiment,
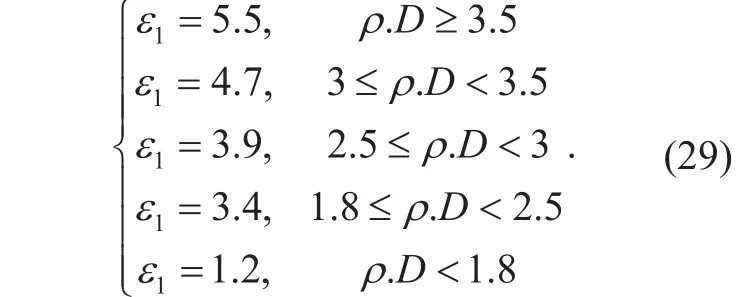
It is emphasized that the selection of α and β in Eq. 27 determines the threshold in Eq.29. Different α and β lead to different detection thresholds in Eq.29. In this paper,our main work is to provide a novel blind detector based on the correlated channel model.

Fig. 2 PsigDsig−noise under various SNRs
As a result, Eq.29 is just one of the reasonable threshold schemes on basis of αβ==0.2 and αβ==0.2 is just for convenience to talk about. The further research on how to obtain the optimum α and β is of our interest next.
IV. SIMULATION EXPERIMENT AND RESULT ANALYSIS
Simulation experiments based on MATLAB platform are made to examine the detection performance in this section. The simulation scenario and parameter setting are the same as the settings in figure1 except the channel type and detection scheme. In figure 3-5, after the generation of OFDM signal, the different signal attenuation models (AWGN, Rayleigh,Rician) are considered into the signal in the simulation. In addition, the detection probability and false alarm probability here is obtained by virtue of Eq.22-23 and the detection threshold is determined based on ρ.D in Eq.29. The noise variance in figure 3-5 is set as 1 due to condition that the noise is generated with variance one.
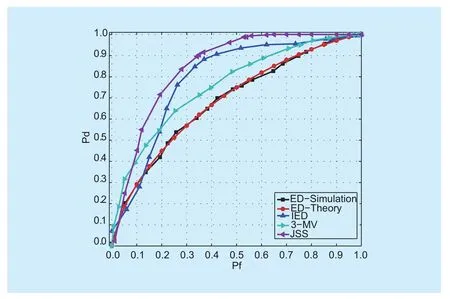
Fig. 3 ROC curve comparisons in AWGN channel (SNR=−10dB)

Fig. 4 ROC curve comparisons in Rayleigh channel (SNR=−10dB)

Fig. 5 ROC curce comparisons in Rician channel (SNR=−10dB)
Figure 3-5 display the ROC (Receiver Operating Characteristic) of several methods for spectrum sensing under various channels.Obviously, the detection performance of JSS increases dramatically for a given probability of false alarm compared with the classical ED method. The detection performance of JSS is also superior to the IED method proposed in[10] and even has much advantage over the fusion method 3-MV (3 represents the number of SU) [9]. To sum up, the classical ED based method always suffers from noise uncertainty,even for the relevant improved methods, resulting in a poor detection performance under strong noise conditions. However, the JSS method performs spectrum sensing with the joint detection of the correlation and variance,which does not depend on the estimation of noise variance and dramatically clears the influence form noise uncertainty. Additionally,the consideration of the correlation between the PU signal and noise makes the detection of idle spectrum more accurate. As a result, the detection performance of JSS is greatly improved in return.
V. CONCLUSIONS
In this paper, a novel method based on joint analysis of variance and correlation for spectrum sensing is proposed, where correlation between the primary signal and noise is taken into consideration. The proposed method dramatically removes noise uncertainty in ED based methods and is independent of the channel type as well as the Probability Distribution Function of channel, which has a wider applicability to the sensing environment. Simulation experiments show that the proposed method outperforms other methods in terms of detection probability and probability of false alarm. Next, further optimizations will be conducted for the removal of noise uncertainty.
Reference
[1] Haykin, S, ‘’Cognitive radio: brain-empowered wireless communications’, IEEE J. Sel. Areas Commun, vol. 23, no. 2, 2005, pp. 201-220.
[2] RAN, I.W., ‘’Functional requirements for the 802.22 WRAN standard’, IEEE 802.22-05/0007r46, Oct. 2005.
[3] Zhang H, Jiang C, Mao X, et al, ‘’Interference-Limited Resource Optimization in Cognitive Femtocells with Fairness and Imperfect Spectrum Sensing’, IEEE Transactions on Vehic-ular Technology, vol. 65, no. 3, 2016, pp. 1761-1771.
[4] Sun H, Nallanathan A, Cui S, et al, ‘’Cooperative Wideband Spectrum Sensing Over Fading Channels’. IEEE Transactions on Vehicular Technology, vol. 65, no. 3, 2016, pp. 1382-1394.
[5] 802.22 Working Group, IEEE P802.22/D0.1 Draft Standard for Wireless Regional Area Networks,[Online]. Available: http://grouper.ieee.org/groups/802/22/, May 2006.
[6] Y.-C. Liang, Y.Z., E.C.Y. Peh, and A.T. Hoang,‘’Sensing-throughput tradeoあ for cognitive radio networks’, IEEE Trans. on Wireless Commun,vol. 7, no. 4, 2008, pp. 1326–1337.
[7] X. Zhou, J. Ma, G. Li, Y. Kwon, A. Soong, ‘’Probability-based combination for cooperative spectrum sensing’, IEEE Transactions on Communications, vol. 58, no. 2, 2010, pp. 463–466.
[8] G. Ganesan, Y.G. Li, ‘’Cooperative spectrum sensing in cognitive radio–part I: two user networks’, IEEE Transactions on Wireless Communications, vol. 6, no. 6, 2007, pp. 2204–2213.
[9] S. Mishra, A. Sahai, R. Brodersen, ‘’Cooperative sensing among cognitive radios’, Proc. IEEE ICC,2006, pp. 1658–1663.
[10] M. López-Benítez and F. Casadevall, ‘’Improved energy detection spectrum sensing for cognitive radio’, IET Communications, Special Issue on Cognitive Comm., vol. 6, no. 8, 2012, pp.785-796.
[11] Riba J, Font-Segura J, Villares J, et al, ‘’Frequency-Domain GLR Detection of a Second-Order Cyclostationary Signal Over Fading Channels’,IEEE Transactions on Signal Processing, vol. 62,no. 8, 2014, pp. 1899-1912.
[12] S. Kozłowski, ‘’Implementation and verification of cyclostationary feature detector for DVB-T signals’, IET Signal Processing, vol. 10, no. 2,2016, pp. 162-167.
[13] Zeng Y, Liang Y C, ‘’Eigenvalue based Spectrum Sensing Algorithms for Cognitive Radio’, IEEE Trans Commun, vol. 57, no. 6, 2008, pp. 1784 -1793.
[14] Pillay N, Xu H J, ‘’Blind eigenvalue-based spectrum sensing for cognitive radio networks’, IET Communications, vol. 6, no. 11, 2012, pp. 1388-1396.
[15] S. M. Kay, Fundamentals of Statistical Signal Processing: Detection Theory, vol. 2. Prentice Hall, 1998.
[16] Zeng Y, Ng T S, ‘’A Semi-Blind Channel Estimation Method for Multiuser Multiantenna OFDM Systems’, Signal Processing IEEE Transactions on, vol. 52, no. 5, 2004, pp. 1419-1429.
[17] Alink M S O, Kokkeler A B J, Klumperink E A M,et al, ‘’Lowering the SNR Wall for Energy Detection Using Cross-Correlation’, IEEE Transactions on Vehicular Technology, vol. 60, no. 8, 2011, pp.3748-3757.
[18] Karar S, Barman A D, ‘’Overcoming the SNR-wall for energy detection using the autocorrelation of cyclic prefix based OFDM signal’, Proc. Communications. IEEE, 2013, pp. 1-5.
[19] Gutiérrez-Gutiérrez, P.M.C.a.J., ‘’On the elementwise convergence of continuous functions of Hermitian banded Toeplitz matrices’, IEEE Trans. Inform. Theory, vol. 53, no. 3, 2007, pp.1168-1176.
[20] Hu Y, Loizou P C, ‘’A subspace approach for enhancing speech corrupted by colored noise’,Speech & Audio Processing IEEE Transactions on,vol. 9, no. 7, 2003, pp. 204-206.
[21] Chengli Sun, J.M., ‘’An eigenvalue filtering based subspace approach for speech enhancement’,Noise control engineering journal, vol. 63, no. 1,2015, pp. 36-48.
杂志排行
China Communications的其它文章
- Migration to Software-Defined Networks: the Customers’ View
- Software Defined Traffic Engineering for Improving Quality of Service
- Towards a Dynamic Controller Scheduling-Timing Problem in Software-Defined Networking
- Efficient Virtual Network Embedding Algorithm Based on Restrictive Selection and Optimization Theory Approach
- A Fast and Memory-Efficient Approach to NDN Name Lookup
- Energy-Efficient Joint Content Caching and Small Base Station Activation Mechanism Design in Heterogeneous Cellular Networks
